-
时序网络是拓扑结构随时间不断变化的网络,其中拓扑结构变化表现为节点或连边的增加或减少。现实社会中,随时间不断变化的网络无处不在[1-2]:在线社交网络、通信网络、合作网络、科研网络;经济网络、交通网络、电力网络;基因调控网络、脑神经网络等等。随着蓝牙、可穿戴设备、传感器等的普及,用于构建时序网络的带时间戳的数据的获取逐渐变得容易,基于时序网络开展的研究成果也逐渐丰富。文献[1-2]总结了时序网络的类型、时序网络拓扑结构的测度、时序网络的模型以及时序网络的传播动力学等;文献[3]用时序图分析时序数据,提出了关于时序图路径的测度;文献[4]总结了时序网络相对静态网络的优势,发现时序网络中从初始状态到最终状态,到达过程更快,需求的控制能量和控制轨迹数量级较小。此外,文献[5]对进化的复杂系统中的排序方法进行总结时,提及了时序网络中的节点重要性排序方法。相对静态网络,时序网络增加了时间维度,考虑了节点间的交互顺序,从而可以更准确地刻画真实系统[6-11]。因此,时序网络模型的构建及其相关理论和应用研究,已经成为网络科学的一个重要研究方向。
关键节点一般是在整个网络中处于核心位置的节点,对整个网络的结构或者功能具有较大的影响力[5, 12-14]。网络中关键节点的确定,可以获得有关实体重要性的先验知识从而预测事情的发展进程,如预测关键元件以防止电网或互联网中的灾难性故障、预测成功的科学家或流行的科学出版物等;可以有效调控传播过程,如精准投放电子商务产品广告以实施产品推广、控制流行病爆发或抑制谣言传播等。关键节点的识别方法之所以能在不同领域中得到应用,一方面取决于方法本身的判别价值,另一方面则是因为信息过载时代大众的多方需求,现如今不论个人还是组织都希望以更低的成本获取实现目的最相关的信息。因此,在网络科学研究中,设计有效的关键节点识别方法,并提出合理的评价模型,有着很强的理论研究和实践意义。
目前,时序网络中的关键节点识别这一问题越来越受到学者的关注。以往对于关键节点的挖掘研究大多是将现实系统抽象成点边相连的静态网络,再依据网络的拓扑结构和动力学特征获得表征节点重要性的度量指标,这些关于网络中节点重要性的研究工作主要集中于网络的静态结构和理论分析上[15-20]。而真实的复杂系统随时间不断进化,个体间的交互呈现出典型的间歇性和阵发性,这使得过去基于静态网络的研究在相当程度上制约了研究成果在实际系统中应用的效果和可靠性。因此,有必要从不同角度总结时序网络中关键节点挖掘的研究进展,并对未来可能的研究方向进行探讨。
本文按如下思路展开:首先分析现有的时序网络建模,再基于时序网络模型从网络的拓扑结构、随机游走动力学以及机器学习的视角概括时序网络中节点的排序测度或中心性指标;然后从网络性能变化、传播动力学以及预测性能三个方面介绍时序网络中关键节点的评价方法;最后在总结和展望部分指出了当前面临的问题和可能的发展方向。
-
时序网络模型的构建是探索时序网络中关键节点识别方法的基础。这里我们所研究的时序网络模型具有一个共同的特征:均不考虑时序网络中节点的增加和移除,而只考虑连边的出现和消失,即所构建的时序网络模型中节点数目保持不变,连边随时间动态变化。其所依赖的数据记录一般以三元组
$(i,j,t)$ 的形式呈现,其中$i$ 和$j$ 表示两个相关的实体(即网络中的节点),$t$ 表示两实体发生作用的时间(即在时间$t$ ,节点$i$ 点$j$ 之间出现连边)。目前,主要的时序网络模型大致可分为三类:基于静态图的时序网络模型,基于快照的时序网络模型和基于明显路径流的时序网络模型[21]。 -
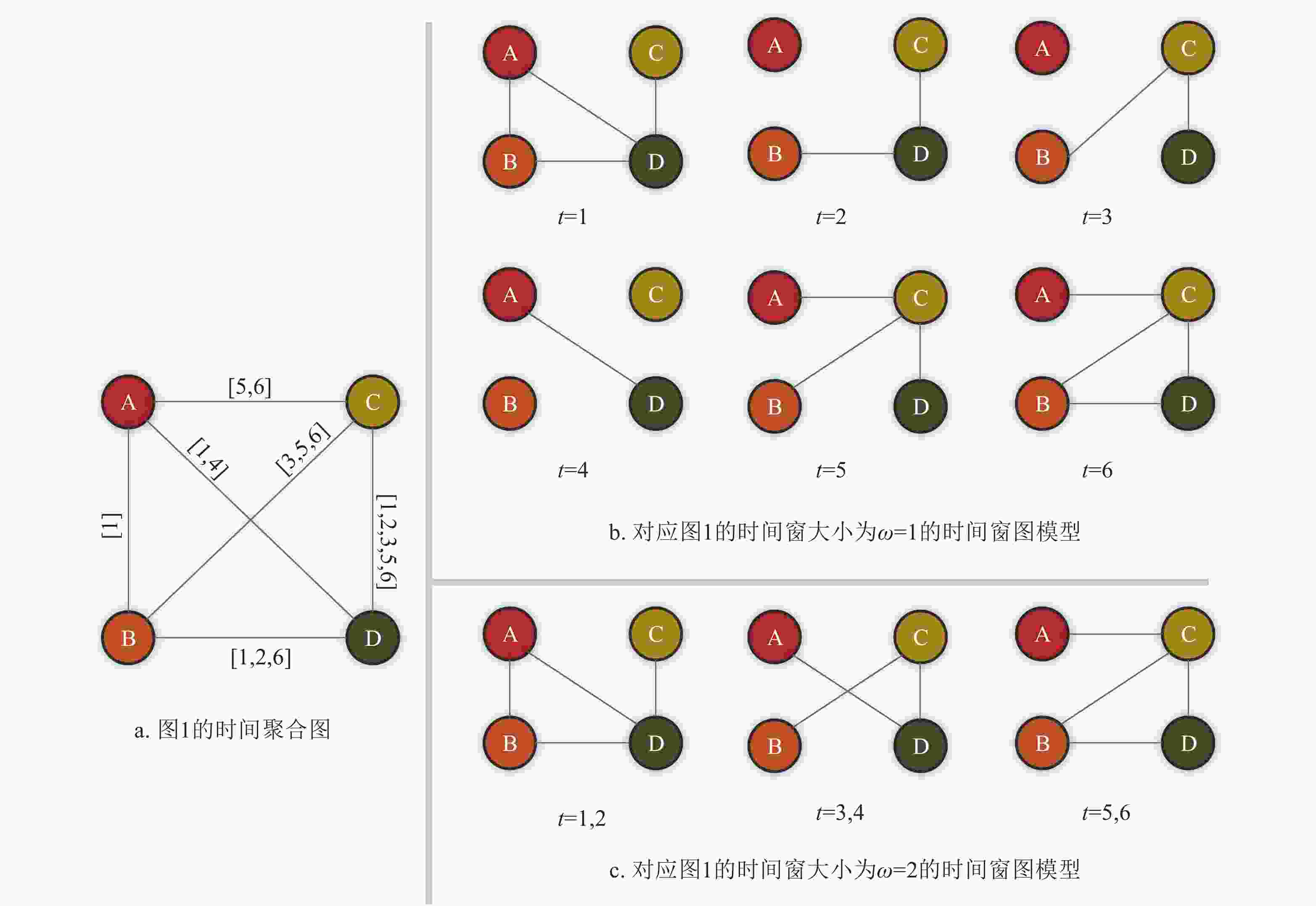
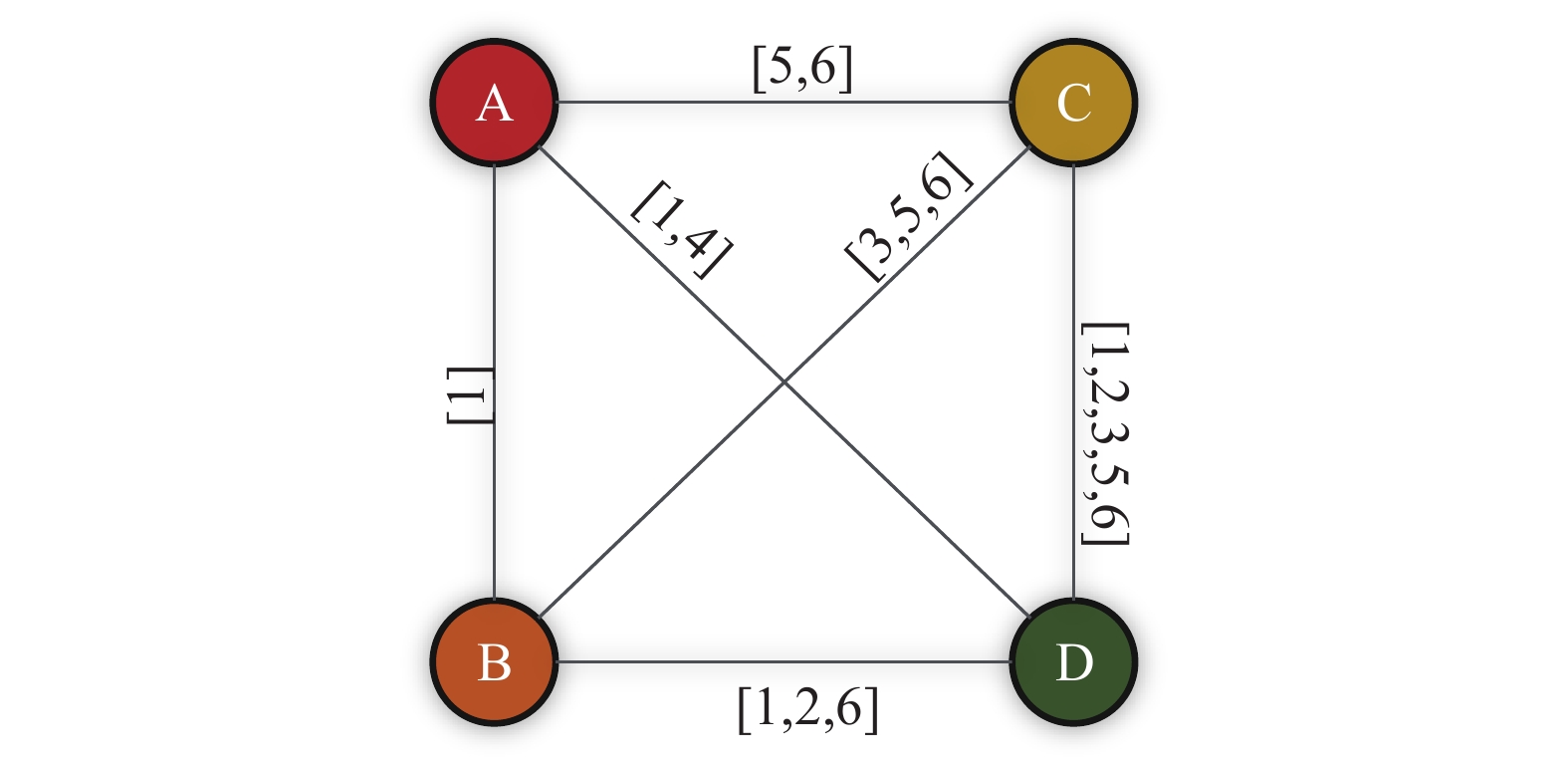
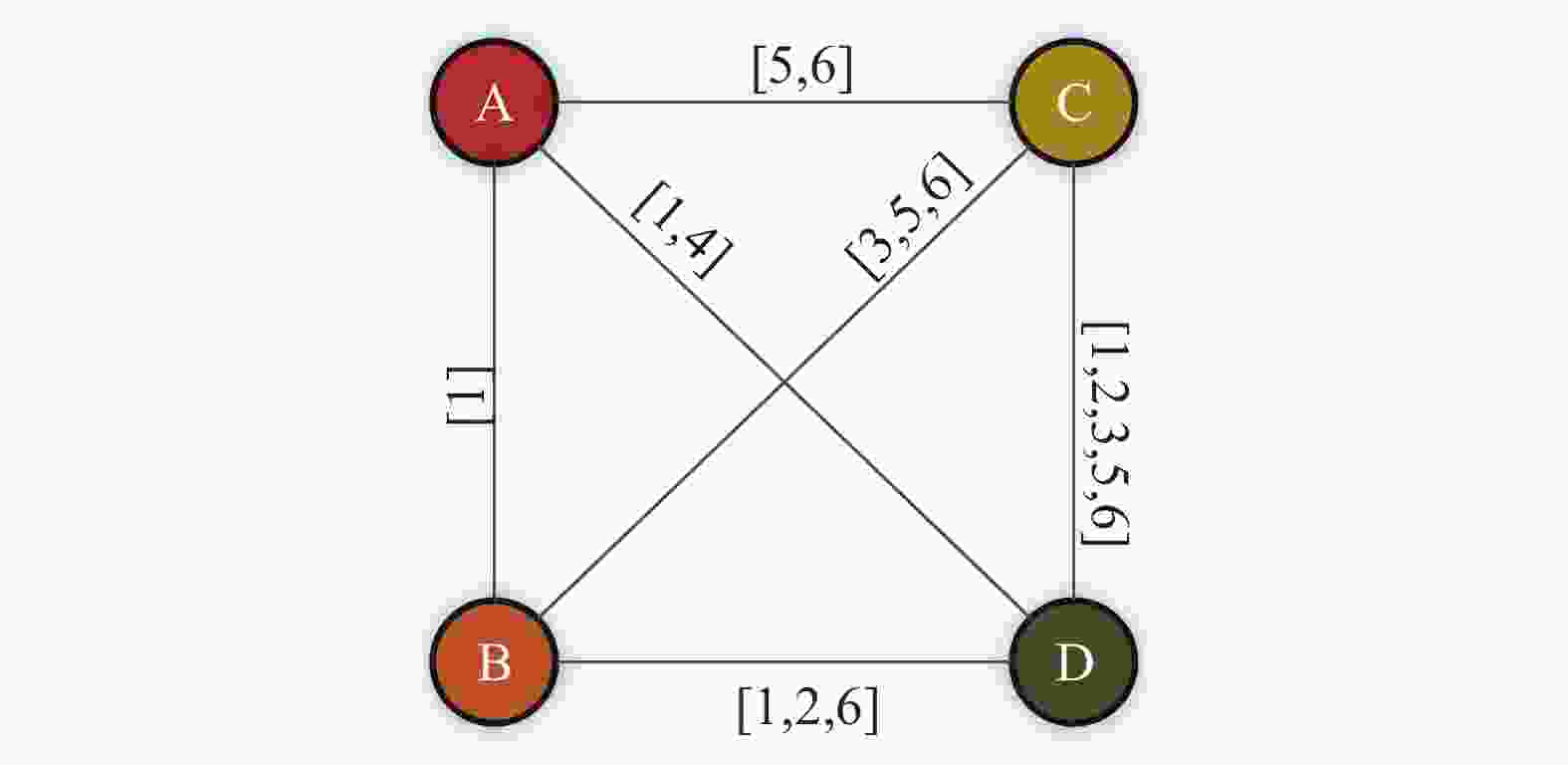
基于静态图的时序网络模型,也叫时间聚合图(time aggregated graphs),是在静态网络拓扑结构的基础上,把节点间交互的时间信息存放在边上的时序网络模型。图1是常见的时间聚合图模型。以连边
$(B,D)$ 为例,时间聚合图1上的序列为$[1,2,6]$ 含交互的具体时间,对应表示节点B和节点D在时间$t = 1$ 、$t = 2$ 和$t = 6$ 时发生交互。此类模型在传统静态网络的基础上增加了时间信息,使其能更真实展示现实系统的演化,但在一定程度上不够直观,且不易用矩阵方式存储和计算。关于此类时序网络模型的研究,文献[22]最早提出并将其用于研究时序网络的连通性和推理问题。之后,文献[23]将模型中的连边建为有向边,研究了社会沟通网络中的信息路径结构;文献[21]将连边上具体的时间信息转化为相应时间的边对应的有和无两种状态,探索了时序网络中中心性测度的计算方法;文献[24]也对时间聚合图提出了改进,其假设连边有向且一对节点之间可能存在带有不同时间戳的多条连边,探索了时序网络中的时序PageRank的表示与计算。此外,文献[1-2]也表示通过静态图表征时序网络可以研究时序网络的时序属性和拓扑属性,并对相关的静态图进行了简单介绍。
-
基于快照(snapshots)的时序网络模型,实际可以看作基于静态图的时序网络模型的拓展,在一定程度上展示了事件的演变过程[25-26]。此类模型的核心在于将研究的整个时间段
$\left[ {0,T} \right]$ 切分成连续的长度为$\omega $ 的$m$ 个快照${N_1},{N_2},\cdots,{N_m}(m = T/\omega )$ 。每个快照可以包含在特定时间瞬间发生的所有事件,也可以是在特定时间窗口内发生的所有事件的静态聚合。根据模型中是否展现快照间的关系,可以将基于快照的时序网络模型分成两类。 -
最常见的基于快照的时序网络模型是如图2所示的时间窗图模型。该模型将快照依次表示为时间聚合图,快照的时间间隔即为时间窗口的大小。图2b中时间窗大小为
$\omega = 1$ ,图2c中时间窗大小为$\omega = 2$ 。快照中的事件根据快照的时间间隔而定。文献[25]首先提出将动态图视为一系列的静态图。在此基础上,不少学者将此类模型作为设计时序网络中关键节点识别方法的基础,提出了时序网络中识别节点重要性或影响力的测度[4, 27-38]。此外,文献[39]在探索动态网络中的中心性测度时,将每个时间窗中的连边定义为有向;文献[40]在设计时序网络的随机游走中心性时,为每个时间窗中的连边赋予权重,其中第
$t$ 个快照中节点对之间的连边权重用时间$(t - 1)\omega $ 到时间$t\omega $ 间该节点对的接触次数表示。应注意,快照时间间隔的选取(即时间窗大小的选择)目前仍是无定论的问题[41-42]。当使用时间窗图模型表示时序网络时,有必要进一步探测模型中不同大小的时间窗口对研究结果的影响。 -
在时间窗图模型的基础上,学者提出了如图3所示的多层图时序网络模型。该模型实质上也是基于快照的时序网络模型,一般由层内关系和层间关系共同定义:层内关系对应一个快照,可理解为时间窗图模型中的一个时间窗图,表征节点间的交互作用;层间关系则表征相邻时间窗中对应节点间的关系,且只有节点自身的连接。就层间关系而言,目前常用的思想有两种,即采用固定的常数和采用相邻时间快照间节点的相似性关系。图3中的
${\omega _i}$ 即是对层间关系的表征。关于此建模方法,文献[43]对其进行了详细的讨论;文献[44]将特征向量中心性推广到时序网络时用到该结构,并采用固定常数表示层间关系;文献[14]则采用基于相邻时间快照间的相似性关系定义层间关系,并基于该模型探索了不同时间层不同节点的特征向量。此外,文献[46]针对层间耦合关系的度量方法进行了分析研究,通过计算不同层间相似性指标值与正理想解和负理想解之间的欧氏距离对度量方法进行排名,发现用优先链接指标度量时序网络时间层的耦合关系,所挖掘出的重要节点准确率最高。
-
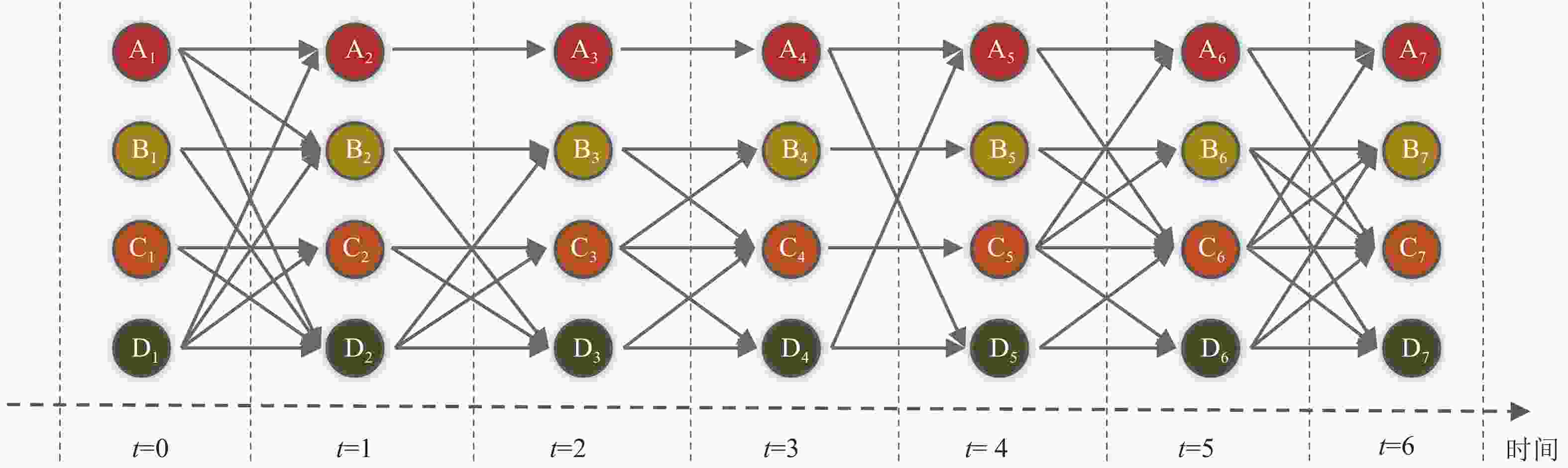
基于明显路径流的时序网络模型,是基于快照的时序网络模型在时间维度上的进一步细化。模型中每个实体对应的节点根据交互信息跨时间复制,而表示潜在信息流的边则用有向边表示并按时间顺序添加。图4是该模型的具体展示,其中水平轴表示时间尺度,竖直轴表示网络中的节点,网络节点的交互只发生在横轴两个相邻的时间层之间,每个节点在前后时间层始终与自身相连。该建模方法已被文献[47]用来研究时序网络的节点重要性评估。文献[3]在2009年也提出了其近似模型,并表明是完全保留原始数据时间信息的时序图模型。之后,文献[48]将其用于时序网络中覆盖中心性的探测,发现大多数的高中心性节点位于某特定时间附近较小的时间窗内,从而获知时序网络中的大量信息只经过少量重要的时序节点传送,且该传送过程发生的时间存在对应的瓶颈期。
此外,文献[49]基于小世界网络和无标度网络拟合Susceptible-Infected-Susceptible(SIS)、Susceptible-Infected-Recovered(SIR)传播模型,建立了基于明显路径流的时序网络模型。当确定初始感染源时,每个时间层节点的状态以及相邻时间层节点间的连边可以完全确定,即整个传播过程生成的时序网络模型固定。应注意,该模型层间不同节点间交互的发生存在激活概率,而不是与所有的邻居节点都存在连边。图5是确定初始传播源,采用SIR模型,根据节点交互情况和状态变化生成的时序网络模型。其中,红色的节点表示感染状态I,绿色的节点表示易感状态S,白色的节点表示恢复状态R;红色的边和绿色的边均表示拟合SIR模型时节点间连边在相应的时间被激活而发生交互,其中红色的边表示t时刻的感染节点致使t时刻的易感节点变成
$t + 1$ 时刻的感染节点,绿色的边则表示$t$ 时刻的易感节点与$t$ 的感染节点或易感节点发生交互而在$t + 1$ 时刻仍然保持易感状态;灰色的边则表示层间节点状态的传递,其中感染状态I以一定概率成为恢复状态R。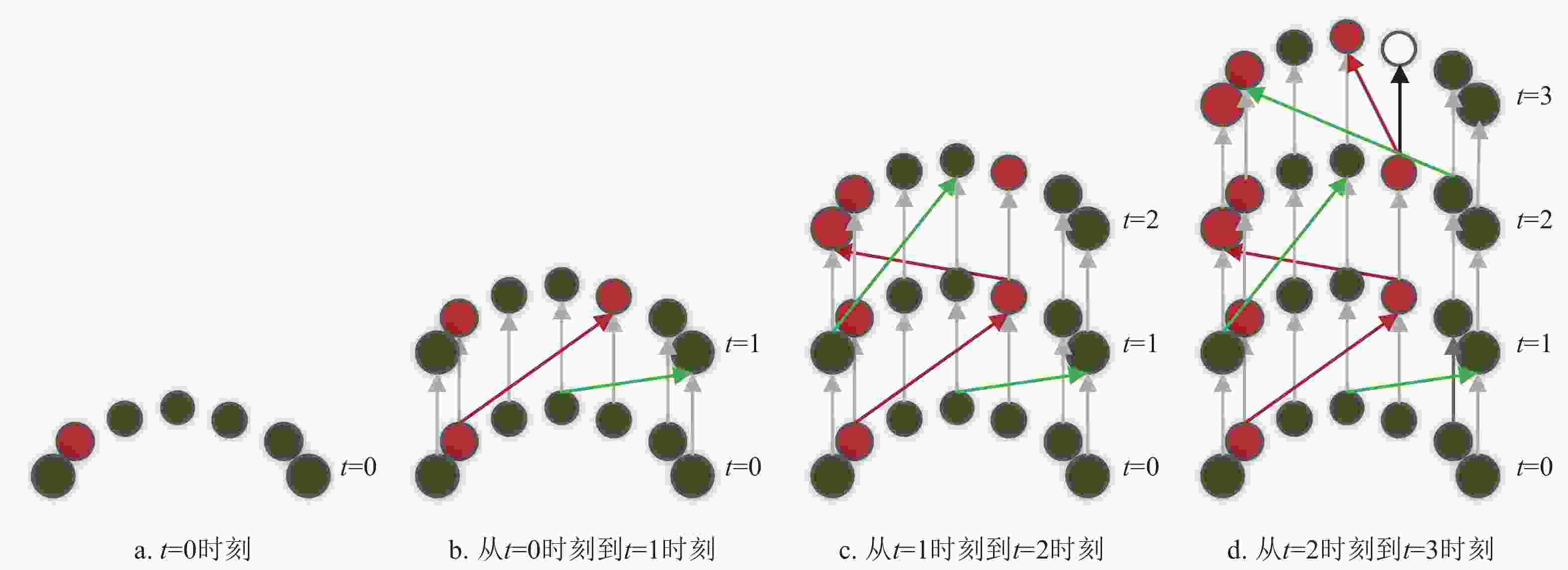
图 5 基于交互数据拟合SIR传播模型生成的基于明显路径流的时序网络模型[52]
-
除了以上三类时序网络模型,也有学者对时序网络的建模及相关特征进行了专门研究。例如,文献[50]除了考虑事件瞬时发生的情况,还考虑事件会持续一段时间的情况,从而在改进时序网络模型的基础上定义了时序平均距离;文献[51]从进化的系统出发,提出了时间窗口大小不等的时间窗图模型,其中时间窗口大小依据事件进化中事件相似性的最大值而确定;文献[52]通过考虑一个与时间有关的哈密顿量,构造了一个随时间变化的网络的虚时间演化算子,从而通过函数解释时序网络模型中的动态变化;文献[53]基于聚合时间图和时间窗图,在每个快照中加入节点和连边的定量属性及方向信息等,然后将
$t$ 时刻的在线社交网络表示为${G_t} = ({V_t},{E_t},{F_{{V_t}}},{F_{{E_t}}},t)$ ,${V_t}$ 是时间$t$ 时刻在线社交网络中的节点集,${E_t}$ 是时间$t$ 时刻在线社交网络中连边的集合,${F_{{V_t}}}$ 是按特征向量${f_v}$ 定量描述节点$v \in {V_t}$ 属性的$\left| {{V_t}} \right| \times \left| {{f_v}} \right|$ 维矩阵,${F_{{E_t}}}$ 是按特征向量${f_e}$ 描述连边$e \in {E_t}$ 属性的$\left| {{E_t}} \right| \times \left| {{f_e}} \right|$ 维矩阵,从而识别大规模时序在线社交网络中的活跃节点;文献[54]提出高阶聚集网络研究时序网络的路径结构,并对静态网络中的介数中心性、接近中心性和可达中心性进行了拓展。该模型背后的思想是每一个$k$ 阶连边$(v,w)$ 表示底层时序网络中长度为$k$ 的时序路径存在的可能性。具体地,将$k - $ 阶静态聚合网络表示为${G^{(k)}} = ({V^{(k)}},{E^{(k)}})$ ,其中${V^{(k)}} \subseteq {V^k}$ 是$k$ 个节点组成的元组的集合,${E^{(k)}} \subseteq {V^{(k)}} \times {V^{(k)}}$ 是连边的集合。简化处理,设置$v = ({v_1} - {v_2} - \cdots - {v_k}) \in {V^{(k)}},{v_i} \in V$ 以及$w = ({w_1} - $ ${w_2} - \cdots - {w_k}) \in {V^{(k)}},{w_i} \in V$ 是$k$ 阶静态聚合图中的节点,$e = (v,w) \in {E^{(k)}}$ 是$k$ 阶静态聚合图中的连边,连边$e$ 存在的条件为两个$k$ 阶静态聚合图中的节点$v$ 和$w$ 恰好有$k - 1$ 个元素重合,即有${v_{i + 1}} = {w_i},i = 1,2, \cdots ,k - 1$ 。此外,文献[55]将时序网络拓展到二分网络,通过简单将其划分为过去的时间窗和未来的时间窗,构建了用户-商品时序二分网络,并基于此提出了商品的流行性和时序新颖性。这些其他时序网络模型有的额外考虑了时序网络的属性和特征,有的直接将模型通过数值形式表征,都为进一步研究时序网络中的节点重要性奠定了基础。 -
时序网络中关键节点识别方法的主要思路是基于时序数据构建时序网络模型,然后通过时序网络的拓扑结构或动力学特征,采用网络节点排序算法,识别关键节点。下面主要从网络的拓扑结构、动力学以及机器学习方法三个方面介绍。
-
节点的重要性很大程度上是由节点在网络上的结构所决定的,依据网络的拓扑结构设计节点的排序指标,是时序网络中关键节点识别的一类重要方法。目前,这些方法的提出多基于静态拓扑指标,如度中心性[56]、介数中心性[57]、接近中心性[58]、k-shell值[59]等。
-
静态网络中,节点中心性最直接的度量是度中心性[56],即一个节点的度越大意味着这个节点越重要。在时序网络,基于度中心性的时序节点中心性指标也同样是最直接的识别重要节点的依据。
文献[47]基于明显路径流的时序网络模型,首先提出了在一段时间
$[i,j]$ 内节点$v \in V$ 的时序度值$$ {D_{i,j}}(v) = \frac{{\displaystyle\sum\limits_{t = i}^j {{D_t}(v)} }}{{(\left| V \right| - 1)(j - i)}} $$ (1) 式中,
${D_t}(v)$ 表示时间$t$ 时节点$v$ 的度,忽视从${v_{t - 1}}$ 到${v_t}$ 的自边$\left( {t = i + 1, \cdots ,j} \right)$ 。节点的时序度值越大,节点越重要,该节点成为关键节点的可能性也越大。文献[37]基于时间窗图模型,对各个时间窗内的时序度中心性值取标准差,提出了时序度中心性偏差值对节点重要性进行排序。具体计算公式如下:
$$ {\rm {Dev}}(i) = \sqrt {\frac{1}{m}\sum\limits_{t = 1}^m {{{({D_t}(v) - \mu (v))}^2}} } $$ (2) 式中,
$\mu (v) = {1 / m}\displaystyle\sum\limits_{t = 1}^m {{D_t}(v)} $ 是节点$v$ 的时序度的均值。节点的时序度中心性偏差值越大,节点越重要,该节点成为关键节点的可能性也越大。基于度中心性的识别方法包括了时序度中心性以及时序度中心性偏差值,两者均聚焦于时序网络中随时间变化节点度值的波动性。其中,时序度中心性通过取不同时间节点度的均值的方式对度值的波动性予以处理,而时序度偏差中心性则在时序度中心性的基础上通过求标准差进一步体现出度值的波动性特征。因此,时序网络中基于度中心性的识别方法优于静态网络的度中心性,但在判断过程中都遵循,所提出的表征节点重要性的指标值越大,节点越重要。此外,一个值得注意的潜在问题是,一个时间序列的中心性指标的均值越大,相应的方差也越大[60]。
-
静态网络中,介数中心性[57]和接近中心性[58]是基于最短路径刻画节点重要性的典型指标。其中,介数中心性考量经过某节点的最短路径的数目,刻画该节点作为中介对信息沿着最短路径传输的控制能力;接近中心性考量每个节点到其它节点的最短路径的平均长度,刻画节点传输信息的速度。
时序网络中,由于路径受连边产生时间和产生顺序的影响,呈现出不同于静态网络中路径的特征[29, 54, 61],主要包括路径的不对称性,未连通的节点更多,消息传递中的滞留或失效等。基于此,许多学者对时序网络中的路径、最短路径以及距离重新进行了考量,定义了时序路径、时序最短路径以及时序距离,并在此基础上提出改进后的时序介数中心性、时序接近中心性以及其他基于时序最短路径的相关指标。
文献[27]以时间窗图模型拟合时序网络,分别从局部和全局的视角出发考虑网络的演化,提出新的时序距离指标,量化和比较了信息扩散过程的速度;然后基于时序路径和时序距离,提出了研究关键节点的时序中心性指标,研究了时序网络中的小世界现象,并将时序中心性指标用于恶意软件的检测[27-29, 62-63]。关于时序路径和时序距离,文献[27]进行了如下定义:
$$ p_{ij}^h = (n_1^{{t_1}},n_2^{{t_2}}, \cdots ,n_k^{{t_k}}) $$ (3) 表示同一时间窗内最大跳跃数为
$h$ 的条件下,从${t_1}$ 时间的节点${n_1}$ 出发在时间${t_k}$ 到达节点${n_k}$ 的时序路径,其中${t_{\min }} \leqslant {t_{k - 1}} \leqslant {t_k} \leqslant {t_{\max }}$ 。假设$Q_{ij}^h$ 是节点$i$ 和节点$j$ 间所有时序路径的集合,若时序路径不存在,则$Q_{ij}^h = \emptyset $ ,说节点$i$ 和节点$j$ 是不连通的节点对,并设定距离$d_{ij}^h = \infty $ 。使用函数
$D(p_{ij}^h) = {t_k} - {t_0}$ 返回相对初始时间${t_{\min }}$ 的传递时间,定义最短时序路径长度为$$ d_{ij}^h = \forall p_{ij}^h \in Q_{ij}^h,\min (D(p_{ij}^h)) $$ (4) 则节点
$i$ 和节点$j$ 间的所有最短时序路径集合为$$ S_{ij}^h = \left\{ {p_{ij}^h \in Q_{ij}^h|D(p_{ij}^h) = d_{ij}^h} \right\} $$ (5) 应注意最短时序路径长
$d_{ij}^h$ 区别于从节点$i$ 到节点$j$ 经过的连边数,且所规定的同一时间窗内的最大跳跃数$h$ 对$d_{ij}^h$ 有重要影响。基于此,文献[28]从静态网络中的介数中心性和接近中心性出发,提出了时序介数中心性和时序接近中心性的计算方法。关于时序介数中心性,不仅需要考虑通过节点的最短路径的数目,同时需要考虑最短路径中节点在将信息传递给下一个节点前保留信息的时长。因此先计算节点i在时间t的时序介数中心性如下:
$$ C_i^B(t) = \frac{1}{{(N - 1)(N - 2)}}{\sum \limits_{\begin{array}{*{20}{l}} {j \in V}\\ {j \ne i} \end{array}}}{\sum \limits_{\begin{array}{*{20}{l}} {k \in V}\\ {k \ne i}\\ {k \ne j} \end{array}}}\frac{{U(i,j,k)}}{{\left| {S_{jk}^h} \right|}} $$ (6) $S_{jk}^h \ne \emptyset $ 时,上述公式成立。其中函数$U$ 表示在从节点$j$ 到节点$k$ 的时序最短路径中,节点$i$ 在时间$t$ 收到了信息,要么持有从过去时间窗中收到的信息,直到某一时间${t^{'}} > t$ 将信息传递给下一节点的路径数目。当$S_{jk}^h = \emptyset $ 时,设定${{U(i,j,k)} / {\left| {S_{jk}^h} \right|}}{\rm{ = 0}}$ 。则节点$i$ 在整个时序网络中的时序介数计算如下:$$ C_i^B = \frac{1}{m}\sum\limits_{t = 1}^W {C_i^B((t \times w) + {t_{\min }})} $$ (7) 式中,
$w$ 表示时间窗的大小;$m$ 表示时序网络中时间窗的总数目。关于时序接近中心性,直接扩展静态网络中的计算公式得到时序接近中心性的计算如下:
$$ C_i^h = \frac{1}{{m(N - 1)}}\sum\limits_{j \ne i \in V} {d_{ij}^h} $$ (8) 所计算的节点的时序介数中心性和时序接近中心性的值越大,表明节点越重要。但是,这两个时序节点重要性评价指标并不总是适用于任何场景。文献[62-63]将所提出的时序指标用于选取关键节点用于阻断恶意软件传播,便发现时序介数中心性与静态指标的效果不显著,但通过选取时序接近中心性高的节点则有显著效果,因为时序接近中心性高的节点可以很快到达大多数节点。
文献[47]基于明显路径流的时序网络模型,也提出了节点结合时序网络特征的介数中心性与接近中心性。相应地,节点的指标值越大,则表明节点越重要。考虑开始时间从
$i$ 到$j - 1$ 不同的$m$ 个时间间隔$\left\{ {[t,j]:0 \leqslant i \leqslant t \leqslant j \leqslant n} \right\}$ ,其中$m = j - i$ ,由此考虑到开始时间不同的影响。任意一个时间间隔$[t,j]$ 内,节点$u$ 到节点$v$ 的时序最短路径定义为从节点${u_t}$ 到节点${v_k}$ 的路径,其中${v_k}$ 是从节点${u_t}$ 出发的路径中最早遇到的$\left\{ {{v_{t + 1}}, \cdots ,{v_j}} \right\}$ 中的节点。基于此,定义时间间隔$[i,j]$ 内节点$v \in V$ 标准化的时序接近中心性计算如下:$$ {C_{i,j}}(v) = \frac{1}{{(N - 1)(j - i)}}\sum\limits_{i \leqslant t < j} {\sum\limits_{u \in V\backslash v} {\frac{1}{{{\Delta _{t,j}}(v,u)}}} } $$ (9) 式中,
${\Delta _{t,j}}(v,u)$ 是时间间隔$[t,j]$ 内节点$v$ 到节点$u$ 的时序最短路径距离,以路径中的连边数表示。当节点$v$ 和节点$u$ 之间不存在时序路径时,${\Delta _{t,j}}(v,u) = \infty $ 。以${S_{x,y}}(s,d)$ 表示在时间间隔$[x,y]$ 内,从节点$s$ 到节点$d$ 的时序最短路径的集合,${S_{x,y}}(s,d,v)$ 是路径中包含节点$v$ 的${S_{x,y}}(s,d)$ 的子集。定义时间间隔$[i,j]$ 内节点$v \in V$ 标准化的时序介数中心性计算如下:$$ {B_{i,j}}(v) = \frac{1}{{V_s^vV_d^v(j - i)}}\sum\limits_{i \leqslant t < j} {{\sum\limits_{\begin{array}{*{20}{l}} {s \ne v \ne d \in V}\\ {{\sigma _{t,j}}(s,d) > 0} \end{array}}}\frac{{{\sigma _{t,j}}(s,d,v)}}{{{\sigma _{t,j}}(s,d)}}} $$ (10) 式中,
$V_s^v,V_d^v \subseteq V\backslash v$ ,${\sigma _{t,j}}(s,d) = \left| {{S_{t,j}}(s,d)} \right|$ ,$ {\sigma _{t,j}}(s,d,v) =$ $ \left| {{S_{t,j}}(s,d,v)} \right|$ 。文献[50]考虑到事件从发生到结束的耗时以及时序路径的不同开始时间等影响,将整个网络视为一个整体,研究了对有限周期内无穷距离的处理方法,并提出了节点对间的平均时序距离计算公式:
$$ \begin{split} & {\tau _{ij}} = \frac{1}{T}[{t_1}\left(\frac{{{t_1}}}{2} + \Delta {t_1}\right) + ({t_2} - {t_1})\left(\frac{{{t_2} - {t_1}}}{2} + \Delta {t_2}\right) + \cdots + \\ & ({t_n} - {t_{n - 1}})\left(\frac{{{t_n} - {t_{n - 1}}}}{2}\right) + (T - {t_n})\left(\frac{{T - {t_n}}}{2} + {t_1} + \Delta {t_1}\right) \end{split} $$ (11) 发现当且仅当节点间有唯一时序路径时,平均时序距离独立于路径的开始时间,也独立于观测时间窗口的时间顺序设置。在此基础上,结合静态网络中的接近中心性公式定义了时序接近中心性:
$$ C_i^T = \frac{1}{{N - 1}}\sum\limits_j {\frac{1}{{{\tau _{ij}}}}} $$ (12) 该时序接近中心性与静态网络的接近中心性类似,值越大,则表明节点越重要。
文献[33]发现时序网络中基于路径的节点重要性评估指标的研究,大多基于数据集起始时间开始的路径,或虽考虑整个数据集时间跨度内的所有路径但多计算单一的静态指标,于是开放地考虑路径的起始时间(即考虑开始于数据集时间间隔内任意时间为起始时间的所有路径),并将静态网络中的接近中心性拓展为随时间不断进化的时序接近中心性指标,从而用于评估任意给定时间任意节点的重要性。具体方法如下:
定义动态网络中从节点
${u_0}$ 到节点${v_k}$ 开始于时间${t_s}$ 的时序路径为连边序列:$$({u_0},{v_0},{t_0}),({u_1},{v_1},{t_1}), \cdots ,({u_k},{v_k},{t_k})$$ 该序列满足:
1)对所有i,
$i = 0,1 \cdots ,k - 1,{u_{i + 1}} = {v_i}$ ;2) 对所有i,
$i = 0,1 \cdots ,k - 1,{t_i} < {t_{i + 1}}$ ;3)
$ {t_0} \geqslant {t_s}$ 。那么该时序路径的间隔时间为
${t_k} - {t_s}$ ,且该间隔时间最短的路径为最短时序路径。定义从时间$t$ 开始节点$u$ 到节点$v$ 的距离为最短时序路径的间隔时间,用${d_t}(u,v)$ 表示;当路径不存在时${d_t}(u,v) = \infty $ 。在此基础上,定义时间$t$ 节点$u$ 的时序接近中心性如下:$$ {C_t}(u) = \sum\limits_{v \ne u} {\frac{1}{{{d_t}(u,v)}}} $$ (13) 实验结果发现,节点重要性随时间变化,捕捉节点全局重要性的聚合指标可能无用,但所提出的时序接近中心性有助于识别整个网络时间间隔内一直很重要的节点,即节点在任意时间的时序接近中心性值都较大,则可以认定该节点在研究的时间间隔内一直很重要。
文献[48]基于时序节点(节点索引和时间的组合)的最快时序路径,提出了两个时序节点在特定时间的中心性测度,并发现这两个中心性测度对于时间标度的变化具有鲁棒性。具体计算如下:令
${{v}} = (v,\tau ),{{u}} = ({{u}},{\tau _{\rm {ldt}}}({{v}},u)),{{w}} = (w,{\tau _{\rm {eat}}}({{v}},w))$ 。根据静态网络中的覆盖率定义了时序网络中的覆盖率。如果满足以下两个条件,则时序节点${{v}}$ 覆盖了节点对$(u,w)$ :1)
${\tau _{\rm {eat}}}({{u}},w){\rm{ = }}{\tau _{\rm {eat}}}({{v}},w)$ ,即如果顺便经过时序节点${{v}}$ ,从时序节点${{u}}$ 出发到达$w$ 的最早时间不变;2)
${\tau _{\rm {ldt}}}({{w}},u){\rm{ = }}{\tau _{\rm {ldt}}}({{v}},u)$ ,即如果顺便经过时序节点${{v}}$ ,到达时序节点${{w}}$ 从$u$ 出发的最晚时间不变。基于时序覆盖率的定义,定义了时序覆盖中心性(TCC),即时序节点
${{v}} = (v,\tau )$ 所覆盖的节点对$(u,w) \in V \times V$ ($V$ 是网络中的所有节点)的比例。如果时序节点${{v}}$ 的TCC的值越接近1,说明该节点覆盖的节点对越多,则其越中心。由于即使移除TCC值大的时序节点,也不能总是使
${\tau _{\rm {eat}}}({{v}},w)$ 更大或者${\tau _{\rm {ldt}}}({{w}},u)$ 更小,所以在时序覆盖率的基础上加入额外的标准定义了边界覆盖率。如果满足一下条件,就说时序节点${{v}}$ 在边界上覆盖了节点对$(u,w)$ :1)$(u,w)$ 被时序节点${{v}}$ 覆盖;2)${\tau _{\rm {eat}}}({{u}},v) = \tau $ 以及${\tau _{\rm {ldt}}}({{w}},v) = \tau $ 。在此基础上,定义时序边界覆盖中心性(TBCC),即时序节点
${{v}} = (v,\tau )$ 在边界上所覆盖的节点对$(u,w) \in V \times V$ ($V$ 是网络中的所有节点)的比例。与时序覆盖中心性相似,如果时序节点${{v}}$ 的TBCC的值越接近1,说明该节点覆盖的节点对越多,则其越中心。实验结果表明真实时序网络中的大量高中心性节点位于特定时间的很窄的时间窗内,而且大量信息会在短时间内通过少量重要的时序节点。最近,文献[64]基于明显路径流的时序网络模型和节点重要性依赖于其邻居重要性的观点,提出了一个时序信息聚集过程(TIG-process)以识别时序网络中的关键节点。基于时序信息聚集过程,作者对比了最快到达路径和最短时序路径在节点重要性识别中的区别,并结合时序信息聚集深度、不同距离邻居的重要性以及节点的初始信息分别给出了依据两种最短路径对节点重要性进行排序的tig-分数。经实验验证发现,在利用最快到达路径评价节点间距离时可以获得更好的识别性能,且可得到最优的信息聚集深度,因为最快到达路径可以聚集更多的时序信息。
基于时序最短路径的指标是时序网络中关键节点识别的一类重要方法,此类方法的重要区别在于定义时序最短路径,是否考虑了如下诸多因素并对其做了何种处理,具体包括路径的起始时间和终止时间、无穷路径的处理方式、信息随时间和距离的衰减,以及最短路径究竟定义为途径节点数目最少的路径还是花费时间最少的路径等。其优势在于通过对时序路径和时序距离的定义,可以更好地捕获时序网络中的时间特性,但同时也存在计算复杂度提高、时间成本增加等问题。
应注意,节点的最短路径数并不总是测量某节点中心性的最好方式,最短路径也并不总是和相应的过程相关,比如疾病总是通过任意路径随机传播,谣言总是沿着长于最短路径的路径进行传播[30]。因此考虑随机游走而不是最短路径的节点识别方法也同样重要,后文将在基于动力学的识别方法中讨论时序网络中基于随机游走的识别方法。
-
K-核分解用于静态网络中的关键节点识别和节点重要性指标设计,早已得到普遍认可和实践。其中文献[59]于2010年首次运用K-核分解获得的节点重要性的排序指标(k-shell),以及在此基础上不少学者进行的相关拓展。比如文献[65]进行加权网络中的K-核分解,提出了加权网络中的ks指标;文献[66]综合考虑目标节点自身K-核的信息和与网络最大K-核的距离,提出新的度量节点重要性的指标;文献[67]基于最小K-核节点邻居集合中最大ks值,提出了更深度的指标。在时序网络的研究中,文献[38]进行了时序网络中基于边的k-shell分解,提出了同时考虑自身和邻居的时序k-core值的表征时序网络中节点重要性的时序指标。其具体的分解方法和节点重要性计算指标如下:
1) 网络快照创建:设置时序网络的时间窗口大小为
$T$ ,得到快照网络序列${N_1},{N_2}, \cdots {N_m}$ ;2) 快照中边权计算:在每个快照网络
${N_t}(t = 1,2, \cdots ,m)$ 中,按照最初的k-shell分解方法求得节点的k-shell值,节点$i$ 在快照${N_t}$ 中的k-shell值记为$k_s^t(i)$ 。对快照${N_t}$ ,连边$(i,j)$ 的权值定义为$\omega _{ij}^t = \min $ $\left\{ {k_s^t(i),k_s^t(j)} \right\}$ ;3) 加权网络
${{{N}}^{{\bf{TK}}}}$ 构建:根据时序数据集创建静态网络,每条连边的权值为${W_{ij}} = \displaystyle\sum\limits_{t = 1}^m {\omega _{ij}^t} $ ;4) 时序k-shell值计算:在加权网络
${{{N}}^{{\bf{TK}}}}$ 中,若${\varGamma _i}$ 是快照网络中节点i的邻居,则同时考虑节点$i$ 自身和邻居的时序k-core值的时序指标${\rm {TK}}(i) = $ $\displaystyle\sum\limits_{j \in {\Gamma _i}} {{W_{ij}}} $ 。与此同时,为验证同时考虑节点自身和邻居的时序k-core值的时序指标
${\rm {TK}}(i)$ 的优越性,作者基于K-核分解提出3个对比时序指标:1) SK:静态k-shell值表征时序网络中的核值;
2) TKD:同时考虑节点自身和邻居的时序k-core值的时序指标
${\rm {TK}}(i)$ 除以节点在静态网络中的度$k(i),即:$ $$ {\rm {TKD}} = \frac{1}{{k(i)}}{\rm {TK}}(i) $$ (14) 3) ASK:快照中的静态k-shell值
$k_s^t(i)$ 取平均,即:$$ {\rm {ASK}} = \frac{1}{m}\sum\limits_{t = 1}^m {k_s^t(i)} $$ (15) 以上4个指标(
${\rm {TK,SK,TKD,ASK}}$ ),均满足节点对应的指标值越大越重要的规律。基于K-核分解的识别方法除了考虑节点的位置属性随时间的变化,同时也考虑了随时间变化节点间的连边关系。通过在不同时间快照中进行K-核分解,初步获得节点的瞬时核值;然后再将节点的瞬时核值映射到静态图的边,并通过边的核值获得节点的全局时序核值。目前在时序网络关键节点识别的研究中,这种从点到边再到点的重要性传递方法尚不常见。
-
静态网络中的特征向量中心性[68]、PageRank[69-70]、枢纽值与权威值(即HITS)分数[71]以及特征因子[72]等基于特征向量的中心性测度,它们作为特征值问题的解决方案出现,常常通过计算中心性矩阵的主特征向量的元素获得,是一类简单且重要的节点重要性排序方法。
将此类方法推广到时序网络,文献[44]提出了一种在有序多层图表示的时序网络中基于特征向量的中心性测度的泛化方法,该方法通过在超中心矩阵(
${\rm {NT}} \times {\rm {NT}}$ 维矩阵)中耦合时间层中心性矩阵(以权重$\omega $ 最相近的时间层间相同节点的耦合)实现。超中心矩阵用权重$\omega $ 表示为$C(\omega )$ ,经转换$\varepsilon = {1 / \omega }$ 变成超中心矩阵$C(\varepsilon )$ 。$C(\varepsilon )$ 的主特征向量${{v}}(\varepsilon )$ 表示所有节点-时间层对$(i,t)$ 的联合中心性(jointly centrality),即表示时间层$t$ 节点$i$ 的中心性,长度为${\rm {NT}}$ ,其中$N$ 为节点数,T为时序网络中的时间层数。具体计算公式如下:$$ C(\varepsilon )v(\varepsilon ) = {\lambda _{\max }}{{v}}(\varepsilon ) $$ (16) 在联合中心性的基础上,将特征向量
${{v}}(\varepsilon )$ 映射为$N \times T$ 维矩阵${{W}}$ ,其中${{{W}}_{it}} = {{{v}}_{N(t - 1)}} + i(\varepsilon )$ ,定义边际节点中心性${x_i}$ (MNC)和边际时间层中心性${y_t}$ (MLC),分别反映节点和时间层的重要性。计算公式分别如下:$$ {x_i} = \sum\limits_t {{W_{it}}} $$ (17) $$ {y_t} = \sum\limits_i {{W_{it}}} $$ (18) 考虑特定的时间层
$t$ ,有节点-时间层对$(i,t)$ 的条件中心性${Z_{it}}$ ,表示时间层$t$ 上节点$i$ 相对于其他节点的重要性。计算公式如下:$$ {Z_{it}} = \frac{{{W_{it}}}}{{{y_t}}} $$ (19) 实验结果证明,所提的条件中心性和边际中心性确实有效,通过这些中心性测度可以动态识别不同时间的重要节点,且中心性测度的值越大,节点越重要。
文献[45]在文献[44]的基础上提出了改进,认为时序网络建模中层间关系的参数表示忽略了不同节点层间连接关系的差异性。受文献[29]对时序相关系数以及文献[32]对时序网络中邻居拓扑重叠系数研究的启发,文中将节点的层间连接关系用邻居拓扑重叠系数表示,提出了基于节点层间相似性的超邻接矩阵时序网络构建方法。利用特征向量中心性指标,获取节点在各个时间层上的重要性排序,从而研究节点重要性随时间变化的轨迹。实验证明,改进后的模型获得的结果优于文献[44]的结果。
基于特征向量的识别方法与前三种基于拓扑结构的识别方法不同,其获得的往往不是全局的节点重要性排序,而多用于获得对应时间快照上的节点重要性排序以及不同时间快照上的重要性排序,因此结果相对而言更微观且更真实,但难以实现全局上节点重要性的判断。
-
除了网络结构之外,节点在网络动力学行为中的影响力也常常被用来作为节点重要性的评判标准。目前,基于网络动力学的识别方法可以粗略的分为基于随机游走和传播动力学两类。
-
过去基于随机游走的方法,如Katz中心性[73]、PageRank[74]、LeaderRank[75]等,已经很好评估了静态网络中的节点重要性。由于基于随机游走的排序算法结合了网络的拓扑属性和动力学属性,且不受网络中信息多少的限制,这使得对随机游走过程的研究以及对网络中基于随机游走的重要节点识别方法的研究逐渐拓展到时序网络。关于时序网络中的随机游走过程:文献[76]研究了时序网络的可达性及连通性,并提出了一种与静态网络中随机游走的谱间隔类似的结构测度表征时序网络的连通性;文献[77]分析了基于时序网络数据的随机游走模型的覆盖率和平均首次通过时间,提出了时间最快的路径和距离最短的路径,发现时序网络中的扩散相对静态图更慢;文献[42]则将时序网络数据和随机游走的稳定状态概率结合起来。关于时序网络中基于随机游走的重要节点识别方法,部分研究是基于静态指标的改进,另有部分研究则是基于时序网络和随机游走的特征,或是基于具体的随机游走过程而提出的全新的指标。
静态图中基于随机游走的经典例子是Katz中心性[78]。其基本观点是节点
$i$ 和节点$j$ 沟通的倾向性可以根据从节点$i$ 到节点$j$ 的长度为$\ell = 1,2,3, \cdots $ 的随机游走路径数目决定,长度$\ell $ 较长的随机游走路径更重要,因此最初的想法是选择适当的参数$\alpha $ 对长度为$\ell $ 的游走路径按照${\alpha ^\ell }$ 进行缩放。节点$i$ 和节点$j$ 之间长度为$\ell $ 的游走路径数目对应邻接矩阵$\ell $ 次幂的元素$\alpha _{ij}^\ell $ 。因此矩阵$S = I + \alpha A + {\alpha ^2}{A^2} + \cdots $ 的元素${s_{ij}}$ 测量了节点$i$ 和节点$j$ 沟通的倾向性。当$\alpha < \rho (A)$ 邻接矩阵的谱半径时,矩阵S可以收敛至${(I - \alpha A)^{ - 1}}$ 。那么,节点$i$ 的Katz中心性为矩阵$S$ 第$i$ 行的和,计算如下:$$ C_i^K = \sum\limits_j {{{[{{(I - \alpha A)}^{ - 1}}]}_{ij}}} $$ (20) 文献[79]建立时间窗图模型,通过类似的原理将Katz中心性拓展到时序网络。以
$A(t)$ 表示第$t$ 个时间窗对应的邻接矩阵,那么任意长度$k$ 的时序游走路径的计数按如下形式获得:$$ {\alpha ^k}A({t_1})A({t_2}) \cdots A({t_k}),{t_1} \leqslant {t_2} \leqslant \cdots \leqslant {t_k} $$ (21) 当
$\alpha < {\min _{{t_m}}}\rho (A({t_m}))$ ,则有沟通性矩阵:$$ { {Q}} = {[I - \alpha A({t_0})]^{ - 1}}{[I - \alpha A({t_1})]^{ - 1}} \cdots {[I - \alpha A({t_m})]^{ - 1}} $$ (22) 根据沟通性矩阵Q,定义传播中心性以及接收沟通性,具体计算分别如下
$$ C_i^{\rm {Broad}} = \sum\limits_j {{Q_{ij}}} $$ (23) $$ C_i^{\rm {Recv}} = \sum\limits_j {{Q_{ji}}} $$ (24) 传播中心性
$C_i^{\rm {Broad}}$ 量化了一个节点i可以在多大程度上将消息传播到时序网络中的其他节点,该值越大,节点的传播能力越强,则节点越重要;接收沟通性$C_i^{\rm {Recv}}$ 则量化了一个节点i能在多大程度上收到其他节点传递的信息,接收沟通性$C_i^{\rm {Recv}}$ 的值越大,节点接收信息的能力越强,信息越多则越可能传播信息,故成为关键节点的可能性会更大。此外,实验结果也表明这两个指标在不同的时间进化的通信网络中可以找出最有影响力的传播者。文献[80]则基于文献[79]提出的时序网络中的沟通性矩阵
$ Q$ ,对文献[81]和文献[82]提出的基于随机游走的沟通介数(communicability betweenness)和分解介数(resolvent betweenness)进行了相关拓展,并提出了基于随机游走的时序网络中节点$v$ 的介数。具体计算如下:$$ \begin{split} & N{B_v}: = \frac{1}{{{{(N - 1)}^2} - (N - 1)}} \times \\ & \sum {\sum\limits_{i \ne j,i \ne v,j \ne v} {\frac{{{{({{ Q}^{[M]}})}_{ij}} - {{({{\bar { Q}}_v}^{[M]})}_{ij}}}}{{{{({{ Q}^{[M]}})}_{ij}}}}} } \\ \end{split} $$ (25) 式中,
${{\bar { Q}}_v}^{[M]}$ 表示调整后的沟通性矩阵;${({{ Q}^{[M]}})_{ij}}$ 是节点$i$ 和节点$j$ 沟通的随机游走路径数;${{\bar { Q}}_v}^{[M]}$ 是移除节点$v$ 后的沟通性矩阵,${({\bar Q_v}^{[M]})_{ij}}$ 表示移除节点$v$ 后节点$i$ 和节点$j$ 沟通的随机游走路径数。该指标可用于评价时间依赖的网络中,节点作为沟通网络中中介的倾向性,指标值越大,节点作为中介的倾向越大,节点成为关键节点的可能性越大。对于时序网络中PageRank值的研究,大多仍然是融入时间因素的静态PageRank值。其中比较典型的是PageRank值计算时加入与时间相关的衰减因子[83-86],或结合不同类型网络(如引文网络[87-88]、体育社会网络[89]、社交网络[90]等)随时间变化的特征改进转移矩阵从而计算静态PageRank值。但是,文献[24]则明确将时序网络表示为基于静态图的时序网络模型(连边上的时间戳表示相应的到达时间),并基于时序网络中的随机游走,结合时间信息和网络动力学提出时序网络中的时序PageRank,以此估计任何时间
$t$ 节点$u$ 的重要性。具体计算方法如下:首先,定义时序网络
$G$ 中时间相关的随机游走,即时序随机游走为如下边序列:$$({u_1},{u_2},{t_1}),({u_2},{u_3},{t_2}), \cdots ,({u_j},{u_{j + 1}},{t_j})$$ 其中
${t_i} \leqslant {t_{i + 1}}(1 \leqslant i \leqslant j - 1)$ 。其次,对节点
$u$ 在静态网络中的PageRank得分$\pi (u)$ 进行调整(如下公式),使得计算只考虑时序游走而不是所有的游走。$$ \begin{split} &{{\text π} (u) = \sum\limits_{v \in V} {{{h}}(v)} \sum\limits_{k = 0}^\infty {(1 - \alpha ){\alpha ^k}} {\sum\limits_{\begin{array}{*{20}{l}} {z \in Z(v,u)}\\ {\left| z \right| = k} \end{array}}}\prod\limits_{(i,j) \in z} {P(i,j)} }=\\ &\;\;\;{ \sum\limits_{v \in V} {\sum\limits_{k = 0}^\infty {(1 - \alpha ){\alpha ^k}} } {\sum\limits_{\begin{array}{*{20}{l}} {z \in Z(v,u)}\\ {\left| z \right| = k} \end{array}}}{{h}}(v)Pr[z|v]}=\!\!\!\\ &\quad{ \sum\limits_{v \in V} {\sum\limits_{k = 0}^\infty {(1 - \alpha ){\alpha ^k}} } {\sum\limits_{\begin{array}{*{20}{l}} {z \in Z(v,u)}\\ {\left| z \right| = k} \end{array}}}Pr[z]} \end{split} $$ (26) 式中,
$Z(v,u)$ 是从节点$v$ 到节点$u$ 的所有游走的集合,$(i,j)$ 表示两个连续的节点之间特定的游走,满足$z \in Z(v,u)$ 。$\prod\nolimits_{(i,j) \in z} {P(i,j)} = {{Pr[z]}/ {k(v)}}$ 表示假设从节点$v$ 开始,只沿着图中的边随机游走到达节点$u$ 的概率。$\alpha $ 表示阻尼因子,是随机游走中按照连边访问的概率;相应地,$(1 - \alpha )$ 则表示按照标准化的个性化行向量${{h}}$ 随机访问的概率。调整过程如下:假设
${Z^T}(v,u|t)$ 是从节点$v$ 出发在时间$t$ 前到达节点$u$ 的所有时序游走的集合,那么某特定的时序游走$z \in {Z^T}(v,u|t)$ 的概率$$ P{r^{'}}[z \in {Z^T}(v,u|t)] = \frac{{c(z|t)}}{{\displaystyle\sum\limits_{{z^{'}} \in {Z^T}(v,x|t) \atop x \in V,\left| {{z^{'}}} \right| = \left| z \right| } {c({z^{'}}|t)} }} $$ (27) 式中,
$c(z|t)$ 是所有从节点$v$ 出发在时间$t$ 前到达节点$u$ 的时序路径的数目,分母表示所有从节点$v$ 出发的与时序游走$z$ 路径长度相等的时序游走数。结合上述两个公式,节点
$u$ 在时间$t$ 的时序PageRank分数的计算公式为:$$ r(u,t) = \sum\limits_{v \in V} {\sum\limits_{k = 0}^t {(1 - \alpha ){\alpha ^k}} } \sum\limits_{z \in {Z^T}(v,u|t) \atop \left| z \right| = k } {P{r^{'}}[z|t]} $$ (28) 同时,由于上述时序PageRank,时序随机游走开始的节点是
$u$ 的概率与从节点$u$ 开始的边的数目成正比。假设向量${{{h}}^{'}}$ 表示游走开始概率向量,即包含所有节点作为游走开始节点概率的向量。则对于节点$u$ ,向量${{{h}}^{'}}$ 中的元素满足对于所有节点$v \in V$ ,有${h^{'}}(u) = {{(u,v,t) \in E} / {\left| E \right|}}$ 。此外,给定个性化的特征向量${{{h}}^{\rm{*}}}$ ,可得个性化的时序PageRank值的计算公式为:$$ r(u,t) = \sum\limits_{v \in V} {\sum\limits_{k = 0}^t {(1 - \alpha ){\alpha ^k}} } \frac{{{{{h}}^{\rm{*}}}(v)}}{{{{{h}}^{'}}(v)}}\sum\limits_{z \in {Z^T}(v,u|t) \atop \left| z \right| = k } {P{r^{'}}[z|t]} $$ (29) 该个性化的时序PageRank值越大,表明节点越重要。在此基础上,文献[24]提出了一个计算该时序PageRank值的算法,并证明算法可以收敛,且当边分布是静态时可以收敛到静态网络的PageRank值。真实数据上的结果也验证了该方法的合理性,并表明其是一个灵活的测度,可以根据网络随时间的变化而调整。
文献[40]提出的TempoRank是基于随机游走的时序网络的中心性测度。该测度是基于明确路径流的时序网络模型在时间周期边界条件下随机游走的固定密度(即达到稳态时可在节点中找到游走者的概率),其与时序网络对应的静止加权有向网络中的节点连入强度高度相近。具体求解过程如下:
1) 定义每个快照中节点对i和j之间的转移概率(以第
$t$ 个快照为例,${\omega _{ij}}(t)$ 表示该快照中节点$i$ 与节点$j$ 间的接触次数,则第$t$ 个快照对应的邻接矩阵为$\omega (t) = ({\omega _{ij}}(t))$ )$$ {B_{ij}}(t) = \left\{ {\begin{array}{*{20}{c}} {{\delta _{ij}}\quad \quad \quad \quad \quad\quad ({s_i}(t) = 0,1 \leqslant j \leqslant N)} \\ {{q^{{s_i}(t)}}\quad \quad \quad \quad \quad \quad\quad \;({s_i}(t) \geqslant 1,i = j)} \\ {{\omega _{ij}}(t)(1 - {q^{{s_i}(t)}})/{s_i}(t)\quad({s_i}(t) \geqslant 1,i \ne j)} \end{array}} \right. $$ (30) 式中,当
$i = j$ 时${\delta _{ij}} = 1$ ,否则${\delta _{ij}} = {\rm{0}}$ ;$q$ 表示节点$i$ 为非孤立节点时,不转移到其他某一邻居节点的概率;${s_i}(t)$ 表示在第$t$ 个快照中节点$i$ 的所有连边数量之和(即节点$i$ 的强度),且有$$ {s_i}(t) = \sum\limits_{j = 1}^N {{\omega _{ij}}(t)\left\{ {\begin{aligned} & { = 0\;\;\;{\text{节点}}i {\text{是孤立点}}}\\ & { \geqslant 1\;\;\;{\text{节点}}i{\text{是非孤立点}}} \end{aligned}} \right.} $$ (31) 当
${s_i}(t) = 0$ 时表示节点$i$ 是孤立点,当${s_i}(t) \geqslant 1$ 表示节点$i$ 是非孤立点;2) 定义时序网络一个周期的转移矩阵为
$$ {{ P}^{tp}} = \prod\limits_{t = 1}^r {B(t)} $$ (32) 式中,
$r$ 表示一个周期内的所有快照的数目,${ B}(t) = ({B_{ij}}(t))$ 是第$t$ 个快照的转移矩阵。定义${P^{tp}}$ 的左侧主特征向量(对应的特征值为1)为$$ {{v}}(1) = ({v_1}(1),{v_2}(1), \cdots ,{v_N}(1)) $$ (33) 那么
${v_i}(1)(1 \leqslant i \leqslant N)$ 即为周期边界条件下节点$i$ 是孤立点的随机游走的固定密度。按$\displaystyle\sum\limits_{i = 1}^N {{v_i}(1)} = 1$ 标准化${{v}}(1)$ 。实际上,${{v}}(1)$ 是当在$t = mr$ 时观测随机游走的固定密度,其中$m \to \infty $ 。由于游走者周期性在不同快照中移动,因此静止状态下的密度仍然会波动。此时,将$t = mr + 1,m \to \infty $ 时的固定密度表示为${{v}}(2) = {{v}}(1){{B}}(1)$ 。那么,长期的固定密度取一个周期内的平均,为$$ \bar v = \frac{1}{r}\sum\limits_{t = 1}^r {{{v}}(t)} ,{{v}}(t) = v(1)\prod\limits_{{t^{'}} = 1}^{t - 1} {{{B}}({t^{'}})} $$ (34) 那么,
$\bar v = ({\bar v_1},{\bar v_2}, \cdots ,{\bar v_N})$ 即为时序网络中基于随机游走的中心性,简称为TempoRank。节点的TempoRank值越大,表明游走达到稳态时游走者到达该节点的概率越大,则节点越重要。文献[39]从时间窗图模型出发,规定每个时间窗为连边不可变的有向图快照
${G_t}$ ,定义其对应的邻接矩阵为$A(t)$ 。基于“如果动态网络中的一个节点经过一段时间对另一个节点产生影响,那么在不同的时间存在一条可以通过中介连接起点和终点的路径”的思想,提出了新的节点中心性测度。考虑未来快照网络$ {G_{{t_{k + 1}}}} $ 的状态除了依赖于当前快照网络$ {G_{{t_{k}}}} $ 的状态,是否还依赖于之前的状态,将时序网络中的信息传播建模为无记忆的动力学过程和有记忆的动力学过程,分别如下。1) 无记忆的动力学过程,未来快照网络
$ {G_{{t_{k + 1}}}} $ 的状态只依赖于当前快照网络$ {G_{{t_{k}}}} $ 的状态。定义节点在时间${t_k}$ 启动信息传输给其邻居的概率为${\beta ^{{t_k}}}$ ,一个节点将其在时间${t_k}$ 接收到的信息在时间${t_{k + 1}}$ 传递给其邻居的概率为$\alpha _k^{{t_{k + 1}}}$ 。衰减因子$\alpha $ 和$\beta $ 随时间和与起点的距离变化,但这里设定${\beta ^{{t_k}}} = \beta ,\alpha _k^{{t_{k + 1}}} = \alpha $ 。那么,在时间${t_1}$ 节点$i$ 发送的信息通过一系列中间节点可以在时间${t_n}$ 到达节点$j$ 的期望量由下面动态中心性矩阵的$(i,j)$ 位置元素给定:$$ \begin{split} & C_{{t_1} \to {t_n}}^d(\beta ,\alpha ) = \beta A({t_1}) + \beta \alpha A({t_1})A({t_2}) + \cdots +\\ & \qquad\quad\; \beta {\alpha ^{n - 1}}A({t_1}) \cdots A({t_n}) \end{split} $$ (35) 令
${\Delta _{1,n}}$ 是信息从时间${t_k}$ 的任意节点$i$ 传递到时间${t_n}$ 的节点$j$ 的时间间隔$\left\{ {{t_1}, {t_2}\cdots ,{t_n}} \right\},(1 \leqslant k \leqslant n)$ 。那么在给定的时间间隔${\Delta _{1,n}}$ 内从节点$i$ 到达节点$j$ 的累积期望信息量由下面累积动态中心性矩阵的$(i,j)$ 位置元素给定:$$ {C^d}(\beta ,\alpha ,{\Delta _{1,n}}) = \sum\limits_{k = 1}^n {C_{{t_k} \to {t_n}}^d(\beta ,\alpha )} $$ (36) 2) 有记忆的动力学过程,未来快照网络
$ {G_{{t_{k + 1}}}} $ 的状态依赖于之前所有快照网络${G_{{t_i}}}\left( {i \leqslant k} \right)$ 的状态。除了上述的衰减因子$\alpha $ 和$\beta $ ,该过程定义了保留概率$\gamma (0 \leqslant \gamma \leqslant 1)$ 和保留时长$m(m \in 1,2, \cdots n)$ ,保留概率$\gamma $ 表示节点保留在时间${t_k}$ 接收到的信息直到时间${t_{k + 1}}$ 的概率。那么,依赖于之前时间邻接矩阵的时间${t_n}$ 的保留邻接矩阵${ R}({t_n})$ 如下:$$ { R}({t_n}) = \left\{ {\begin{array}{*{20}{c}} {A({t_n}) + \gamma A({t_{n - 1}}) + \cdots + {\gamma ^{n - 1}}A({t_1})\,\quad\quad \;\;\;\; n < m} \\ {A({t_n}) + \gamma A({t_{n - 1}}) + \cdots + {\gamma ^{m - 1}}A({t_{n - m + 1}})\,\quad n \geqslant m} \end{array}} \right. $$ (37) 保留动态中心性矩阵为:
$$\begin{split} & RC_{{t_1} \to {t_n}}^d(\beta ,\alpha ,\gamma ) = \beta R({t_1},\gamma ) + \beta \alpha R({t_1},\gamma )R({t_2},\gamma ) +\\ & \qquad\quad \cdots + \beta {\alpha ^{n - 1}}R({t_1},\gamma ) \cdots R({t_n},\gamma ) \end{split} $$ (38) 时间间隔
${\Delta _{1,n}}$ 内的保留累积动态中心矩阵为:$$ R{C^d}(\beta ,\alpha ,\gamma ,{\Delta _{1,n}}) = \sum\limits_{k = 1}^n {RC_{{t_k} \to {t_n}}^d(\beta ,\alpha ,\gamma )} $$ (39) 根据
$RC_{ij}^d(\beta ,\alpha ,\gamma ,{\Delta _{1,n}})$ 的值,可以找到对节点$j$ 最有影响力的节点$i$ ;同时根据$RC_{ji}^d(\beta ,\alpha ,\gamma ,{\Delta _{1,n}})$ 的值,可以找到对节点$i$ 最有影响力的节点$j$ 。且值越大,影响力越大。文献[34]针对动态时序网络,提出了一种实时性消息传播过程中识别“最近较活跃”节点的方法。该方法扩展静态网络中基于通路(walk,即点边交替出现的序列)的节点中心性分析方法到随时间动态演化的网络中,将消息传播路径分解到时间-空间两个维度上,并利用两个衰减因子分别刻画消息的效用随传播路径长度衰减及随时间推移衰减这两种自然特性,利用节点的历史相遇信息,得到了节点传播能力的量化分析函数,以此刻画节点对时效性消息的相对传播能力。基于快照的时序网络模型,具体方法如下:
1) 定义动态通路为在一个非递减的离散时间序列
${t_1} \leqslant {t_2} \leqslant \cdots \leqslant {t_r} \leqslant \cdots \leqslant {t_k}({t_1},{t_k} \in T)$ 上的顶点与连边的序列${v_i}{e_1}{v_1}{e_2} \cdots {v_m}{e_r}{v_{m + 1}} \cdots {e_w}{v_j}$ 构成节点$i$ 到节点$j$ 的长度为$w$ 的动态通路,当且仅当第r个快照的邻接矩阵满足${({A_r})_{{i_m}{i_{m + 1}}}} \ne 0$ 。2) 从空间维度和时间维度出发,将动态通路明确分为空间通路(在某单一静态快照中形成的通路)和时间通路(由若干个连续或不连续快照的通路组成)。
3) 考虑所有动态通路的组合,按照“长步长通路赋予较小权重,短步长通路赋予较大权重”的原则,计算动态时序网络的动态中心性指标矩阵
${D^t}$ ,有$$ {D^t} = {e^{\beta {A_1}}}{e^{\beta {A_2}}} \cdots {e^{\beta {A_t}}} $$ (40) 式中,
${({D^t})_{ij}}$ 表示截止到第$t$ 个快照,节点$i$ 和$j$ 之间的影响力大小。展开得$$ \begin{split} & {D^t} = \Bigg(I + \frac{{\beta {A_1}}}{{1!}} + \frac{{{\beta ^2}A_{_1}^2}}{{2!}} + \cdots + \frac{{{\beta ^x}A_{_1}^x}}{{x!}} + \cdots \Bigg) \times \\ & \Bigg(I + \frac{{\beta {A_2}}}{{1!}} + \frac{{{\beta ^2}A_2^2}}{{2!}} + \cdots + \frac{{{\beta ^x}A_2^x}}{{x!}} + \cdots \Bigg) \times \cdots \times \\ &\quad \Bigg(I + \frac{{\beta {A_t}}}{{1!}} + \frac{{{\beta ^2}A_t^2}}{{2!}} + \cdots + \frac{{{\beta ^x}A_t^x}}{{x!}} + \cdots \Bigg) \end{split} $$ (41) 展开式中,在节点的动态通路加权公式中加上
$n \times n$ 维矩阵$I$ ,表示节点把消息传递给自己。同时,可以发现在同一拓扑快照内长度为$w$ 的通路按照${{{\beta ^w}} / {w!}}$ 的方式衰减,利用不同拓扑快照完成的长度为$w$ 的通路按照${{{\beta ^w}} / {({l_1}}}!{l_2}! \cdots {l_r}!)$ 的方式衰减,其中$w = {l_1} + {l_2} + \cdots + {l_r}$ 表示跨越了$r$ 个拓扑快照完成了长度为$w$ 的通路,并在第$r$ 个快照中完成了$w$ 中的${l_r}$ 步。4) 由于上述衰减方式只按照通路长度对时间通路与空间通路进行衰减,并未体现节点之间产生影响的先后顺序或消息的实时性,即未考虑动态通路产生的时间先后顺序。因此考虑节点之间消息(影响)的实时性,基于“节点之间的影响强度或消息效用往往随时间推移而递减”的原则,提出了传播实时消息的关键节点发现的迭代计算公式:
$$ {{{Q}}^{k + 1}} = ({{\rm{e}}^{ - \alpha \Delta {t_{k + 1}}}}{{{Q}}^k} + I)({{\rm{e}}^{\beta {A_{k + 1}}}} + I) - I $$ (42) 式中,
$\Delta {t_{k + 1}} = {t_{k + 1}} - {t_k}$ ,${t_k}(k \in N)$ 表示第$k$ 个快照中产生的动态通路的发生时刻,值越大表示距当前时刻越近,那么该时刻的影响越重要,该时刻产生的动态通路受到较少的衰减;${{{Q}}^k} \in n \times n$ 维矩阵表示截止到第$k$ 个快照时动态时序网络中节点的影响力矩阵,${{{Q}}^0} = {\bf{0}}$ ;${A_k}$ 表示第$k$ 个快照网络对应的邻接矩阵;$\alpha $ 为时间衰减因子,表示对时间因素按照自然指数方式衰减;${{\rm{e}}^{ - \alpha \Delta t}}$ 表示对不同静态快照中的通路按照快照产生的先后顺序进行衰减,并保证同一个静态快照中不同长度的空间通路在时间维度上的衰减程度相同。另外,${{{Q}}^{t + 1}}{\bf{1}}$ 、${({{{Q}}^{t + 1}})^{\rm T}}{\bf{1}}$ 分别表示节点传播、获取实时性消息的关键程度,其中1是$n \times 1$ 维向量$1 = {(1,1, \cdots ,1)^{\rm T}}$ 。应用于移动P2P社会网络的实验结果验证了该方法的可行性,且可以明显观察到利用该方法选出来的关键节点作为消息传播的起始节点,网络消息的覆盖速率明显提升。所述的基于随机游走的识别方法,主要有3类:1)基于Katz中心性的时序拓展指标,分别有传播中心性(衡量节点传递消息给其他节点的程度)、接收沟通性(衡量节点接收其他节点传递消息的程度)以及时序介数中心性(节点作为沟通网络中中介的倾向性),该类指标主要可用于沟通网络或信息传播网络中起重要传播作用的关键节点识别;2)基于PageRank值的时序拓展指标,除了考虑时间衰减和网络的特征的静态PageRank值,还有一类通过将静态PageRank的随机游走拓展到时序随机游走获得的时序PageRank值。该时序PageRank更能反映网络中真实的信息流动,且考虑到边分布的变化能造成节点重要性的变化,估计的是任何时间t节点u的重要性,同时该时序指标也很好地实现了与静态网络中PageRank值的契合,即当网络生命周期中边分布不变时,时序PageRank值等于静态PageRank值;3)基于时序网络中随机游走的时序指标,此类指标脱离了静态网络中对节点重要性判断的指标,仅仅通过时序随机游走便可估计节点的重要性,其中的关键在于时序网络随机游走中转移概率、衰减因子的设定。在此基础上,计算游走达到稳态时到达对应节点的概率,以及以节点作为消息传播的起点,通过随机游走查看消息覆盖的速率,从而可获得节点的重要性衡量指标。相对基于最短路径的识别方法,基于随机游走的识别方法所考虑的信息传播路径范围不再受限于时序最短路径,也无需再考虑用路径长度最短还是时间间隔最短定义时序最短路径。
-
目前,大多数网络传播动力学相关研究主要基于经典的流行病传播动力学模型[91-92]。真实世界中的观点、消息、疾病、恶意软件等的传播都可以建模成网络中的传染过程[93-96],传染过程可以用于研究网络的结构特性及其组成部分的相对重要性[31]。从该角度出发,提出时序网络中表征节点传播影响力的指标,是基于网络拓扑结构识别方法的重要延伸和拓展。
文献[97]从网络结构的拓扑特征和动力学属性出发,提出了可以直接用于静态网络中有影响力传播者定位的对动力学敏感的中心性(dynamics-sensitive centrality)指标,并通过在4个真实网络中进行SIR传播模型和SI传播模型的拟合,发现该指标优于度中心性、k-shell指标以及特征向量中心性。具体方法如下:
针对简单无向连通网络
$G = (V,E)$ ,节点数$n = \left| V \right|$ ,连边数$e = \left| E \right|$ ;${{A}} = \left\{ {{a_{ij}}} \right\}$ 为对应的邻接矩阵,节点对$i$ 和$j$ 之间存在连边时${a_{ij}} = 1$ ,否则${a_{ij}} = 0$ ,对角线元素均为0。对称实值矩阵A可表示为${{A}} = {{Q}}{{\varLambda}} {{{Q}}^{\rm T}}$ ,其中${{\varLambda}} = {\rm {diag}}({\lambda _1},{\lambda _2}, \cdots ,{\lambda _n})$ ,${\lambda _1} \geqslant {\lambda _2} \geqslant \cdots \geqslant {\lambda _n}$ 是矩阵A的降序排列的特征值,${{Q}} = [{{{q}}_1},{{{q}}_2}, \cdots ,{{{q}}_n}]$ ,${{{q}}_i}$ 是特征值${\lambda _i}$ 对应的特征向量。${{x}}(t)(t > 0)$ 表示在时间1和$t$ 之间节点被感染的累积概率的近似值,则${{x}}(t) - {{x}}(t - 1)(t > 1)$ 表示在时间$t$ 节点感染的概率的近似值。如果节点$i$ 是唯一的初始感染节点,则有${x_i}(0) = 1$ ,${x_{j \ne i}}(0) = 0$ 。在SIR传播模型中,假定易感节点与感染节点接触的感染概率为$\beta $ ,感染节点康复的恢复概率为$\mu $ 。则对$t = 1$ ,有$$ {{x}}(1) = \beta {{Ax}}(0) $$ (43) 对
$t > 1$ ,有$$ {{x}}(t) - {{x}}(t - 1) = \beta {{A}}{[\beta {{A}} + (1 - \mu ){{I}}]^{t - 1}}{{x}}(0) $$ (44) 式中,I为单位矩阵。令
${{H}} = \beta {{A}} + (1 - \mu ){{I}}$ ,则:$$ {{x}}(t) - {{x}}(t - 1) = \beta {{A}}{{{H}}^{t - 1}}{{x}}(0) $$ (45) 因此,在时间1和
$t$ 之间节点被感染的累积概率近似为:$$ {{x}}(t) = \sum\limits_{r = 2}^t {[{{x}}(r) - {{x}}(r - 1)]} + {{x}}(1) = \sum\limits_{r = 0}^{t - 1} {\beta {{A}}{{{H}}^r}{{x}}(0)} $$ (46) 定义
${S_i}(t)$ 为在时间$t$ 节点$i$ 的传播影响,以节点$i$ 为初始感染节点时其他所有节点感染概率的总和表示。若${{{e}}_i} = {(0, \cdots ,0,1,0, \cdots ,0)^{\rm T}}$ 是只有第$i$ 个元素为1的$n \times 1$ 维向量,则在时间1和$t$ 之间节点被感染的累积概率$x(t)$ 可表示为$$ {{x}}(t) = \sum\limits_{r = 0}^{t - 1} {\beta {{A}}{{{H}}^r}{{{e}}_i}} $$ (47) 由此可知,以节点
$i$ 为初始感染节点,${{x}}(t)$ 实际为$\beta {{A}},\beta {{AH}}, \cdots ,\beta {{A}}{{{H}}^{t - 1}}$ 的第$i$ 列元素之和。因为${{x}}(0) = {{{e}}_i}$ 且${{{S}}_i}(t)$ 是${{x}}(t)$ 的所有元素之和,故:$$ {{{S}}_i}(t) = {[{(\beta {{A}} + \beta {{AH}} + \cdots + \beta {{A}}{{{H}}^{t - 1}})^{\rm T}}{{L}}]_i} $$ (48) 式中,
${{L}} = {(1,1, \cdots ,1)^{\rm T}}$ 是所有元素为1的$n \times 1$ 维向量。由于${{{A}}^{\rm T}} = {{A}}$ ,${H^{\rm T}} = H$ ,${{AH}} = {{HA}}$ ,故所有节点的传播影响可写为:$$ \begin{split} &{{ S}}(t) = \sum\limits_{r = 0}^{t - 1} {\beta {{A}}{{{H}}^r}L} = \sum\limits_{r = 0}^{t - 1} {\beta {{A}}{{{H}}^r}\left(\sum\limits_{i = 1}^n {{{{e}}_i}} \right)} =\\ & \sum\limits_{i = 1}^n {\sum\limits_{r = 0}^{t - 1} {\beta {{A}}{{{H}}^r}{{{e}}_i}} } = \sum\limits_{i = 1}^n {\left( {\sum\limits_{r = 0}^{t - 1} {\beta {{A}}{{{H}}^r}{{{e}}_i}} } \right)} \end{split} $$ (49) $\displaystyle\sum\limits_{r = 0}^{t - 1} {\beta {{A}}{{{H}}^r}{{{e}}_i}} $ 表示以节点i为初始感染节点所有节点时间1和$t$ 之间被感染的累积概率。因此,${{S}}(t)$ 可以被简单解释为以每个节点为初始感染节点的$n$ 种情况下的感染概率之和,这表明关系中的潜在对称性,即在无向网络中,影响力越高的节点越容易被感染。依据${{H}} = \beta {{A}} + (1 - \mu ){{I}}$ ,可知${{H}}$ 和${{A}}$ 有相同的特征向量,且${{H}}$ 的对应第$i$ 个特征向量${q_i}$ 的第$i$ 个特征值为$\beta {\lambda _i} + 1 - \mu $ 。当$\beta {\lambda _i} + 1 - \mu < 1$ 时,即$\beta /\mu < 1/{\lambda _1}(\mu \ne 0)$ 时,${{{H}}^t}L$ 在时收敛到零向量,则${{S}}(t)$ 可被写作为$$ \begin{split} &\qquad\qquad {{S}}(t) = \beta {{A}}{({{I}} - {{H}})^{ - 1}}{{L}}= \\ & [(\beta /\mu ){{A}} + {(\beta /\mu )^2}{{{A}}^2} + \cdots + {(\beta /\mu )^t}{{{A}}^t}]{{L}} \end{split} $$ (50) 在SI传播模型中,
$\mu = 0$ 时若$t \to \infty $ ,则${{S}}(t)$ 也将无穷大。在此基础上,文献[98]将该指标拓展到时序网络,基于时间窗图模型拟合SIR传播模型,提出了时序网络中有影响力传播者定位的时序对动力学敏感的中心性(temporal dynamic-sensitive centrality)指标,并通过在3个真实时序网络和一个理论时序网络拟合SIR传播模型,发现其结果优于利用静态和时序的度中心性、接近中心性、介数中心性的结果。该方法的改进在于,该指标的计算基于时间窗图模型,传播过程中的邻接矩阵是时间窗图模型中各个快照对应的邻接矩阵,而不始终是简单无向连通图对应的邻接矩阵A。具体方法如下:
用邻接矩阵
${{A}}(t)$ 表示第$t$ 个时间窗的快照网络,仍然假设${{x}}(t)$ 表示不超过时间$t$ 节点被感染的累积概率,${{P}}(t) = {{x}}(t) - {{x}}(t - 1)$ 表示节点在时间步$t$ 被感染的概率,其中${{P}}(0) = {{x}}(0)$ 表示初始状态;假定SIR传播模型中易感节点与感染节点接触的感染概率为$\beta $ ,感染节点康复的恢复概率为$\mu $ 。假设只有唯一的初始感染节点$i$ ,那么${x_i}(0) = 1$ ,则有$$ {{x}}(1) = \beta {{A}}(1){{x}}(0) $$ (51) $$ \begin{split} &\qquad\qquad\qquad {{x}}(t) - {{x}}(t - 1)= \\ & \beta {{A}}(t)\prod\limits_{r = 1}^{t - 1} {[\beta {{A}}(r) + (1 - \mu ){{I}}]} x(0),t > 1 \end{split} $$ (52) 用数学归纳法求解可得:
$$ {{x}}(t) = \sum\limits_{r = 0}^{t - 1} {\beta {{A}}(r + 1){{{H}}^{(r)}}{{x}}(0)} $$ (53) 式中,
${{{H}}^{(r)}} = \displaystyle\prod\limits_{\alpha = 1}^{t - 1} {[\beta {{A}}(\alpha ) + (1 - \mu ){{I}}]} $ ,${{{H}}^{(0)}} = {\bf{1}} $ 。${{{S}}_i}(t)$ 表示传播影响,即在时间$t$ 节点$i$ 的感染概率的总和$$ {{{S}}_i}(t) = {[{(\beta {{A}}(1) + \beta {{A}}(2){{{H}}^{(1)}} + \cdots + \beta {{A}}(t){{{H}}^{(t - 1)}})^{\rm T}}{{V}}]_i} $$ (54) 因为
${{A}}{(t)^{\rm T}} = {{A}}(t)$ ,${[{{{H}}^{(t)}}]^{\rm T}} = {{{H}}_*}^{(t)}$ ,所以有$$ {{S}}(t) = \sum\limits_{r = 0}^{t - 1} {\beta {{{H}}_*}^{(r)}{{A}}(r + 1){{V}}} $$ (55) 式中,
${{V}} = {(1,1, \cdots ,1)^{\rm T}}$ ;${{S}}(t)$ 即为本文所提出测量节点在时序网络中传播影响的指标。该指标值越大,说明节点的传播影响越大,则节点越重要。基于传播动力学的关键节点识别方法并不常见,但其往往作为测量标准,评价其他识别方法的好坏。后面在时序网络中关键节点识别方法的评价指标中将进一步说明。
-
目前,机器学习结合复杂网络的研究逐渐增多,基于网络的机器学习算法的应用越来越广泛[99],包括理论研究中网络的社区检测[100]、动态网络中的链路预测[101]或网络中的动态链路预测[102],以及现实社会中水电气等供应网络中的可达性[103],城市运输网络中的交通预测[104]等。
将机器学习方法用于网络中关键节点的挖掘也引起了大量学者的关注。如文献[105]将社会网络分析引入机器学习模型来预测P2P行业的用户违约,首先基于知名互联网金融公司闪银所提供的大规模脱敏数据,从复杂网络的视角加以分析,然后将分析结果转化为机器学习的输入特征,用支持向量机的方法挖掘其内在的关联,从而实现利用用户的社会网络结构性质预测用户的信用情况。
此外,文献[106]也通过机器学习的方法预测了社会网络中最有力的说服者,其以时间T为界,以在此之前的数据作为训练数据,剩余的数据作为测试数据,探索了一种基于机器学习的预测关键节点的间接方式——首先基于社会网络理论,提出社会影响
${I_k}$ 、实体相似${R_k}$ 及结构等效${M_k}$ 这3个影响实体说服能力的影响因素;然后以此3因素为特征,个体的决策${D_k} \in (0,1)$ 为标签,通过50次自助采样训练决策树模型取平均值以估计个体间的说服概率:$$ {p_{ij}} = \sum\nolimits_{50} {\frac{{{n_D} + mP({D_k} = 1)}}{{{n_L} + m}}} $$ (56) 式中,
${n_D}$ 表示训练数据中节点的${D_k} = 1$ 的数目;${n_L}$ 表示所达叶节点中训练数据的数目,$m$ 取$\sqrt {{n_L}} $ ,$P({D_k} = 1)$ 是训练数据中${D_k} = 1$ 的先验概率。然后根据说服概率提出表征个体说服能力的指标值如下:$$ {c_i} = \sum\limits_{{v_j} \in V,j \ne i} {{p_{ij}}{c_j}} $$ (57) 式中,
${p_{ij}}$ 是所求的实体$i$ 说服实体$j$ 的概率;${c_j}$ 表示实体$i$ 服能力,由说服概率和其他所有实体${v_j} \in V,j \ne i$ 的说服能力共同决定。通过幂迭代算法求解表征实体说服能力的指标值,值越大,则对应的实体越重要。文献[55]基于用户-对象的二分网络,将数据划分为过去的时间窗和未来的时间窗,以识别并预测电子商务平台或者社交媒体平台中的关键节点,即未来流行或重要的对象(商品、对象或推文等)。具体地,考虑复杂网络中驱动节点流行性的3个影响因子(偏好连接、最近的流行度以及衰变),提出表征节点在未来时间流行度或重要性的预测分数模型如下:
$$ {s_0}(t,{T_p}) \sim \frac{{\displaystyle\sum\limits_u {{{\rm{e}}^{\gamma ({T_{uo}} - t)}}} }}{{\displaystyle\sum\limits_O {\displaystyle\sum\limits_u {{{\rm{e}}^{\gamma ({T_{uo}} - t)}}} } }} \frac{{({k_o}(t) - \lambda {k_o}(t - {T_P}))}}{{\displaystyle\sum\limits_O {({k_o}(t) - \lambda {k_o}(t - {T_P}))} }} $$ (58) 式中,
${T_p}$ 表示过去的时间窗;${s_0}(t,{T_p})$ 表示基于过去时间窗${T_p}$ 在时间$t$ 对象的预测分数;$\lambda $ 是调整新颖性和总流行性的参数;${T_{uo}}$ 表示用户$u$ 消费对象$o$ 的时间;$\gamma $ 为自由参数。然后,基于过去时间窗中的数据用梯度下降算法求解出模型中的参数,迭代过程如下:$$ \begin{split} & {\lambda _i} = {\lambda _i} - \alpha \Delta e \left( {\frac{{\partial {s_0}(t,{T_p})}}{{\partial {\lambda _i}}}} \right) \\ &{\gamma _i} = {\gamma _i} - \alpha \Delta e \left( {\frac{{\partial {s_0}(t,{T_p})}}{{\partial {\gamma _i}}}} \right) \end{split} $$ (59) 式中,
$\Delta e$ 表示误差。最后通过预测分数模型进行未来时间窗中对象流行度或重要度的预测,并根据准确率、新颖性、时序新颖性以及AUC等值评价模型的好坏。该应用虽然未涉及具体的时序信息,但在一定程度上引入了时序概念,为后续开展将机器学习方法用于时序网络中关键节点识别的研究提供了参考。 -
除以上3类方法外,有些研究从其他视角提出了关键节点的识别方法。如文献[36]提出马尔科夫时序网络模型,没有直接给出时序网络中的Katz中心性的静态表示,而是通过成本最低不断调整马尔科夫时序网络中边的权重以优化给定节点的Katz中心性测度,解决的是一个关键节点识别的优化问题。
文献[107]通过对办公大楼中面对面接触的时序数据的研究,发现一种无需完全了解时序网络,便可以根据部门的组织结构,获得关键节点的方法。具体地,根据各个部门中节点在部门内的连边与在部门间的连边数量,将节点分为居住者(有更多的部门内连边)、闲逛者(有更多的部门间连边)和连接者(部门内连边和部门间连边各占一半),其中连接者被定义为重要节点,因为他们的介数中心性更大,且在增强部门间的沟通方面起重要作用。
文献[53]结合图挖掘和序列挖掘,基于静态结构属性和时序行为属性提出了一个识别信息扩散中活跃的有价值的节点的方法。具体的流程如下:首先,建立定量的时序聚合图,在此基础上根据社区探测算法揭示结构属性,并选择活跃有价值节点的候选者,这些候选者是社区的核心且是连接两个社区的桥梁;然后,运用序列挖掘算法从活动记录中提取候选者的行为趋势;最后,通过分析行为趋势的空间-时间特征,将候选者分为活跃节点与非活跃节点,于是得到活跃的有价值的节点。该方法通过对时间行为特征的跟踪,无需分析每个网络快照的结构。因此,具有相对较低的计算成本,且不会丢失活动有价值节点识别的准确性。
鉴于很多现有的时序网络中的节点中心性指标很少考虑不同快照中节点影响的关系,而一般而言,如果一个节点连接到更多在后续的快照中有更多邻居的节点,那么该节点可能是一个更重要的传播者。文献[35]从信息论的角度将静态网络中基于熵的中心性扩展到了时序网络,定义
$L_i^t$ 是快照$t$ 中节点${v_i}$ 的邻居集合,$\left| {L_i^t} \right|$ 是快照$t$ 中节点${v_i}$ 的邻居集合中节点的数目,定义$H_i^t$ 是快照$t$ 中节点${v_i}$ 的信息,则有$$ H_i^t = - \sum\limits_{m = 1}^{\left| {L_i^t} \right|} {\frac{{C_{\left| {L_i^t} \right|}^m}}{{{2^{\left| {L_i^t} \right|}}}}{{\log }_2}\frac{{C_{\left| {L_i^t} \right|}^m}}{{{2^{\left| {L_i^t} \right|}}}}} $$ (60) 式中,
$C_{\left| {L_i^t} \right|}^m$ 表示节点${v_i}$ 的邻居中有$m$ 个邻居受影响的组合;${{C_{\left| {L_i^t} \right|}^m}/ {{2^{\left| {L_i^t} \right|}}}}$ 示节点${v_i}$ 的所有邻居中有$m$ 个邻居受影响的概率。对$H_i^t$ 标准化,有$$ \tilde H_i^t = \frac{{H_i^t}}{{\displaystyle\sum\limits_{j \in V} {H_j^t} }} $$ (61) 由于快照
$t$ 中节点${v_i}$ 的影响不仅由其邻居数决定,还受其邻居影响的影响。基于此,定义$I_i^t$ 为快照$t$ 中节点${v_i}$ 的影响,则有$$ I_i^t = \frac{{pI_i^{t + 1} + \frac{{\displaystyle\sum\limits_{k \in L_i^t} {I_k^{t + 1}} }}{{\displaystyle\sum\limits_{j \in V} {I_j^{t + 1}} }}}}{{\displaystyle\sum\limits_{q \in V} {\left(pI_q^{t + 1} + \frac{{\displaystyle\sum\limits_{k \in L_q^t} {I_k^{t + 1}} }}{{\displaystyle\sum\limits_{j \in V} {I_j^{t + 1}} }}\right)} }} $$ (62) 式中,
$p \in [0,1]$ ,表示$t + 1$ 时刻的节点${v_i}$ 在多大程度上决定$t$ 时刻的节点${v_i}$ 的影响。该指标值越大,说明节点在快照$t$ 中影响力越大,则该节点在相应的时间越重要。特别地,由于在最后一个时间戳图中,不知道下一快照中节点${v_i}$ 的邻居影响,所以认为节点${v_i}$ 的影响仅由其感染的不确定性决定,即有$$ I_i^t = \tilde H_i^t $$ (63) 同时由于当
$t = 1$ 时,各节点的影响考虑了相邻节点在整个时间段内的累积效应,所以作者利用$t = 1$ 处各节点的影响衡量节点在计算机病毒时序网络传播过程中的重要性。 -
评价时序网络中关键节点识别方法的效果有多种不同的角度,可以依据节点在网络的结构和功能中的重要性,同时也可以与其他已有指标进行对比。一般而言,网络中节点的重要性排序主要从网络性能的变化、传播效果的好坏、指标间的相关性三个角度验证。
-
网络性能是考察节点对网络结构的影响力的评价指标。节点删除法是常用的利用网络性能变化评价节点重要性的方法,其有累积删除和依次删除两种思路[108]。假设网络时序性能为
$E(G)$ ,首先按节点识别方法对节点重要性排序,再计算表征时序网络性能变化的评价指标。具体有如下思路:1) 分别衡量节点未删除时的网络性能以及节点删除后的网络性能,然后比较两者的差值[24, 38, 45, 48]。记累积删除
$\sigma $ 比例节点后的时序网络性能为$E(G\backslash \sigma )$ ,则计算如下:$$ V(G) = \frac{{E(G) - E(G\backslash \sigma )}}{{E(G)}} $$ (64) 若两者差值越大,则说明节点对网络性能的影响越大,同时也说明节点越重要,识别方法性能越好。
2) 设定网络性能的阈值,观察达到该阈值所需删除的节点比例[108-109]。记累积删除
${\sigma _{th}}$ 比例节点后网络性能达到阈值为${E_{th}}(G)$ ,即有${E_{th}}(G\backslash \sigma ) = {E_{th}}(G)$ ,则计算如下:$$ V(G) = \frac{{{\sigma _{th}}}}{{\left| N \right|}} $$ (65) 若删除的节点比例越少,则说明节点对网络性能的影响越大,同时也说明识别出的节点越重要,识别方法性能越好。
3) 与上面直接删除前
$\sigma $ 比例重要节点不同,这里按节点重要性排序依次删除网络中的节点${v_i}(1 \leqslant i \leqslant \left| N \right|)$ 直至网络中所有节点被删除。记节点${v_i}$ 删除后的网络性能为$E(G\backslash {v_i})$ ,则计算如下:$$ V(G\backslash {v_i}) = \frac{{E(G\backslash {v_1}...{v_{i - 1}}){\rm{ - }}E(G\backslash {v_1}...{v_{i - 1}}{v_i})}}{{E(G\backslash {v_1}...{v_{i - 1}})}} $$ (66) 该结果衡量单个节点依次移除后网络性能的变化。若值越大,说明节点越重要,同时也说明识别方法有好的性能。
目前,针对时序网络的衡量指标尚不多见,所用的方法大多是将静态网络中网络性能的变量替换为时序网络中定义的时间相关的变量。其中,较为常见的用于评价时序网络关键节点识别方法的网络时序性能指标是网络时序效率和网络时序最大连通分量:
1) 网络时序效率:时序网络中信息传播效率的衡量指标,较小的值意味着信息能够在时序网络中更快传播开。该时序性能指标来源于静态网络中的网络效率[110],即所有节点接近中心性的均值,定义如下:
$$ {\rm {Eff}}(G) = \frac{1}{{N(N - 1)}}\sum\limits_{ij} {\frac{1}{{{d_{ij}}}}} $$ (67) 式中,
${d_{ij}}$ 表示节点对$(i,j)$ 间的最短路径。在时序网络中,基于不同的时序最短距离或时序接近中心性的定义,文献[27]、文献[33]以及文献[45]将网络的时序效率定义为:$$ {E_t}(G) = \frac{1}{{N(N - 1)}}\sum\limits_{u \ne v} {\frac{1}{{{d_t}(u,v)}}} $$ (68) 式中,
${d_t}(u,v)$ 表示开始时间为$t$ 的节点对$(u,v)$ 间的时序距离,时序距离通过时序最短路径计算。开始时间t不同时,同一节点对$(u,v)$ 间的时序距离也不一定相同。此外,当节点对$(u,v)$ 间不存在时序路径时,${d_t}(u,v) = \infty $ 。2) 网络时序最大连通分量:衡量时序网络可达性的指标,是时序网络最大连通图中的节点数占整个网络所有节点的比例[38]。该时序性能指标来源于静态网络中的最大连通分量,即最大连通分量中节点的比例,定义如下:
$$ {\rm {LCC}}(G) = \frac{{\mathop {\max }\limits_{1 \leqslant i \leqslant k} (\left| {{C_i}} \right|)}}{N} $$ (69) 式中,
$\left| {{C_i}} \right|(1 \leqslant i \leqslant k)$ 表示第$i$ 个连通图中的节点数目;$k$ 表示图中连通分量的数目。在时序网络中,求解该时序性能指标的关键在于获取时序网络中最大连通分量中的节点数,具体有如下两种方法:① 基于时序网络模型,选取初始时间的节点
$u$ ,依次遍历各个时间点直至结束,统计可到达的节点数目为$\left| {{\Omega _u}} \right|$ [111],则有$$ {{\rm {LCC}}^{\rm T}} = \frac{{\mathop {\max }\limits_{u \in V} (\left| {{\Omega _u}} \right|)}}{N} $$ (70) ② 分别求解各快照的最大连通分量并取均值[38],即
$$ {{\rm {LCC}}^{\rm T}} = \frac{1}{m}\sum\limits_{t = 1}^m {\frac{{\mathop {\max }\limits_{1 \leqslant i \leqslant k} (\left| {C_i^t} \right|)}}{N}} $$ (71) 式中,
$\left| {C_i^t} \right|(1 \leqslant i \leqslant k)$ 表示第$t$ 个快照中第$i$ 个连通图中的节点数目;$k$ 表示图中连通分量的数目。 -
基于传播模型的评价方法主要考虑节点在网络信息传递中的作用。其中,常用的传播模型有SI传播模型、SIS传播模型和SIR传播模型。三类模型共呈现出节点的3种状态:易感染状态(S, Susceptible)即未来可能被感染的健康状态,感染状态(I, Infected)即患病状态,以及移除状态(R, Removed)即从感染状态恢复并具备抵抗力。
在SI传播模型中,只存在易感染状态(S)的节点以概率
$\beta $ 被感染状态(I)的节点感染,即有:$$ S(i) + I(j)\mathop \to \limits^\beta I(i) + I(j) $$ (72) 在SIS传播模型中,易感染状态(S)的节点以概率β被感染状态(I)的节点感染,感染状态(I)的节点以概率γ恢复成为易感染状态(S)的节点,即有:
$$ \left\{ \begin{array}{l} S(i) + I(j)\mathop \to \limits^\beta I(i) + I(j) \\ I(i)\mathop \to \limits^\gamma S(i) \\ \end{array} \right. $$ (73) 在SIR传播模型中,假设易感染状态(S)的节点以概率β被感染状态(I)的节点感染,感染状态(I)的节点以概率γ成为移除状态(R)的节点,则有:
$$ \left\{ \begin{array}{l} S(i) + I(j)\mathop \to \limits^\beta I(i) + I(j) \\ I(i)\mathop \to \limits^\gamma R(i) \\ \end{array} \right. $$ (74) 一般而言,在时序网络中基于传播模型对时序网络的节点识别方法的效果进行评价,主要在时序网络模型中模拟这三类传播模型的时序传播。该过程与静态网络中拟合的区别在于,节点对间连边产生和消失的时序性,因此传播也需考虑连边形成的时间。具体做法为基于几种关键节点的识别方法对节点的重要性进行排序,则几种关键节点识别方法性能评判的具体思路有:其一,取相同数目最重要节点群为初始感染源,最能促进“疾病”传染的关键节点识别方法则更优;其二,取相同数目最重要节点群为免疫群体,最能阻止“疾病”传染的关键节点识别方法则更优。
关于“疾病”传染的衡量指标,即是对节点传播能力的衡量。一般而言,在SI传播模型或者SIS传播模型中,常常以达到稳定状态时被感染的节点数目表示;在SIR传播模型中,常常则以能够传播的平均距离表示。与此同时,也有不少文献基于时序网络模型的特征提出了新的评价指标,如文献[31]基于真实时序数据集构建时间窗图模型拟合SI传播模型,定义每个节点
$i$ 的传播影响力为一半节点患病时间。具体方法为:假设节点$i$ 是传播源并在时间${t_{0,i}}$ 第一次出现,其他节点都是易患病节点,到时间${t_i}$ 有一半节点患病,那么定义节点$i$ 的传播能力为$$ {T_i} = {t_i} - {t_{0,i}} $$ (75) 式中,Ti值越小,表示节点i对疾病的传播能力越强,即节点i更重要。进一步,从疾病免疫的角度提出单个节点的感染延迟率:
$$ {\tau _i} = {\left\langle {\frac{{T_j^i - {T_j}}}{{{T_j}}}} \right\rangle _{j \ne i}} $$ (76) 以此作为评估节点影响力的衡量。其中
$T_j^i$ ,${T_j}$ 表示节点$i$ 免疫与未免疫,以节点$i$ 以外的任意节点$j$ 为传播源,一半节点患病的时间。该指标对SI传播模型时序拟合中的所有不同开始时间以及所有初始传播源$j \ne i$ 取平均。当节点$i$ 的${\tau _i}$ 值越大时,说明节点$i$ 的免疫更能阻断疾病传播,则节点$i$ 更重要。在提出评估单个节点免疫影响指标的基础上,基于SI传播模型,文献[31]提出了对节点群$V$ 免疫的评价指标:节点群的感染延迟率${\tau _V}$ 以及平均爆发规模比${i_V}$ 。其中,$$ {\tau _V} = {\left\langle {\frac{{T_j^V - {T_j}}}{{{T_j}}}} \right\rangle _{j \notin V}} $$ (77) 式中,
$T_j^V$ 、${T_j}$ 分别表示节点群$V$ 中所有节点免疫与未免疫,以节点群$V$ 以外的任意节点$j$ 为传播源,一半节点患病的时间。该指标对SI传播模型时序拟合中的所有不同开始时间以及所有初始传播源$j \notin V$ 取平均。$$ {i_V} = - {\left\langle {\frac{{I_j^V - {I_j}}}{{{I_j}}}} \right\rangle _{j \notin V}} $$ (78) 式中,
$I_j^V$ 、${I_j}$ 分别表示节点群$V$ 中所有节点免疫与未免疫,以节点群$V$ 以外的任意节点$j$ 为传播源,患病节点的数量。该指标对SI传播模型时序拟合中的所有不同开始时间以及所有初始传播源$j \notin V$ 取平均。文献[49]提出了一种网络影响的基准方法,用TKO分数表示。该方法结合了超级传播者和免疫过程的影响,同时还包括感染的时间,能够克服不同的测度针对具体的网络结构有效以及传统方法的不足,从而更准确地测量节点对传播的影响。具体过程如下:
1) 选择初始传播源,基于时序网络运行疾病传播模型,同时获取每个节点的状态以及每次迭代的时间。其中,感染节点的数量及感染持续的时间是基于该初始传播源的疾病量级(magnitude)。
2) 对于对应时序网络中的每个时间层的节点,实施移除操作分析。即移除某节点,运行相同的动力学模型,测量疾病量级的变化,获得该节点的基于初始传播源的边际感染分数。
3) 使用每个节点作为初始感染源,执行过程1)和2),获得每个时间层每个节点基于不同的初始传播源的边际感染分数。取平均值作为所求的TKO分数。
TKO分数是一个全方面的经验度量,可以捕获到节点在每个时期影响疾病传播的潜力,常用于评估其他影响测量方法的准确性,是一种有效的基准测量方法。
此外,文献[112]基于8个人类接触数据集构建时序网络、静态网络及全连通网络进行SIR传播模型仿真。提出两个评估指标:灭绝时间和爆发规模。定义没有感染的个体存在时,该传染病消失,灭绝时间即为从爆发到消失的时间间隔;定义传染病消失时,恢复状态个体的比例定义为爆发规模。
-
时序网络中的关键节点识别方法主要实现对节点重要性的排序,预测时序网络中全局最重要的节点或者特定时间层的重要节点。若设定某一基准识别方法或已知节点真实的重要性排序,则可基于相关性评价所提出识别方法的预测性能。常用的相关性评价指标有Kendall’s τ相关系数[113]以及Spearman相关系数[114],两者的取值范围均为[−1, 1],值越大,相关性则越强,即说明节点重要性的排序方法更优。
文献[97]在评估所提出的时序对动力学敏感的中心性这一关键节点识别方法的性能时,在4个时序网络中拟合SIR传播模型,以一段时间后感染节点的数目衡量节点的传播影响,选择随机选择初始感染节点的结果为基准,同时获得根据静态度/介数/接近中心性、文献[47]提出的时序度/介数/接近中心性、时序对动力学敏感的中心性这七个指标选择初始感染节点的传播影响;然后分别计算按照七个指标选取初始感染节点的传播影响与随机选择初始感染节点的传播影响的Kendall’s τ(肯德尔系数),发现根据时序对动力学敏感的中心性选取初始感染节点的传播影响的相关系数最大,从而得知所提出方法有更高的精度。
文献[45]在提出时序网络中的各时间层网络上节点的特征向量中心性(SSAM)的方法后,基于两个实证网络数据,用节点删除法得到节点时序全局效率差值并排序,然后利用Kendall’s τ(肯德尔系数)计算特征向量中心性与时序网络效率差值的相关性;同时按照文献[44]提出的SAM方法选取不同的参数以相同的方法计算相应的Kendall’s τ系数。对比可知,SSAM方法得到的Kendall’s τ系数结果大部分比SAM方法的高,说明其得到节点重要性排序更为准确。
此外,在利于过去的节点重要性排序结果表征未来的节点重要性排序时,常见的有将时间
$t$ 的重要节点作为下一时间$t + 1$ 的预测[47],或划分训练集和测试集将训练集中的重要节点作为测试集的预测[55, 105],一般在已知真实的节点重要性排序时可计算其与预测的节点重要性排序之间的相关系数,从而评价识别方法的好坏。在此情况下,准确率[106]也是常见的评价指标。其表示预测的前$K$ 个重要节点在真实排序中的数目占比。计算如下:$$ {\rm {precision}} = \frac{{\left| {{P_K} \cap {R_K}} \right|}}{{\left| {{R_K}} \right|}} $$ (79) 式中,
${P_K}$ 和${R_K}$ 为选取预测排序和真实排序的前$K$ 点序列。准确率越高,说明节点识别方法的性能越好。 -
本文在介绍时序网络建模的基础上,总结了现有主要的时序网络中关键节点的识别方法以及时序网络中针对关键节点识别方法的评价方法,为后续开展设计时序网络中节点重要性指标提供了重要参考。关于时序网络中关键节点的识别方法的总结见表1。然而,时序网络中的关键节点识别方法大多是静态网络中的中心性测度基于时序网络模型的拓展,对关键节点识别方法的评价指标也多源自静态网络。虽然此类改进确实起到了提升关键节点识别方法性能的效果,但仍然存在诸多亟待解决的问题:
表 1 时序网络中的关键节点识别方法
归类 时序网络中关键
节点识别方法方法示例 基准方法/模型 方法说明 优点 缺点 基于拓扑结构的识别方法 基于度中心性的识别方法 时序度中心性[47] 度中心性 聚焦于时序网络中随时间变化节点度值的波动性 简单直观,时间复杂度低 只能反映节点在整个时间段内的全局局部重要性 时序度中心性偏差值[37] 基于最短路径的识别方法 时序介数中心性[28, 47] 介数中心性 聚焦于重新度量时序网络中的路径、最短路径及距离 计算节点随时间推移的全局重要性,即始点或中介的传播能力 时间复杂度高,不适用大型网络 时序接近中心
性[28, 33, 47, 50]接近中心性 时序覆盖中心性[48] —— 基于K-核分解的识别方法 时序k-shell值[38] K-核值 聚焦于点的时序重要性到边的全局重要性再到点的全局重要性的传递 通过时序网络的分解重构和节点的重要性传递获取在整个时间段内节点的全局重要性 时间复杂度高,只能获得节点的全局重要性 基于特征向量的识别方法 边际节点中心性边际时间层节点中心性节点在特定时间层上的条件中心性[44] 静态网络中基于特征向量的中心性测度,如特征向量中心性PageRank枢纽值与权威值特征因子等 基于时序网络模型在超中心性矩阵中耦合时间层中心性矩阵,再求解主特征向量 获得的往往是对应时间快照上的节点重要性排序以及同一节点不同时间快照上的重要性排序,结果更微观真实 构建的超中心性矩阵需要耦合时间层中心性矩阵,计算复杂度高,且层间的关系定义不明 时序特征向量中心性[45] 基于动力学的识别方法 基于随机游走的识别方法 传播中心性和接收沟通性[78] Katz中心性 基于所提出的任意长度的时序随机游走路径,以及静态网络中的Katz中心性计算方法计,从而计算时序网络中的沟通性矩阵 1.通过对随机游走的时序定义以及对时间或空间维度信息衰减程度的表征,更真实刻画了网络中消息传递的路径,所得的节点重要性的评判结果更真实
2.相对基于最短路径的识别方法,基于随机游走的识别方法所考虑的信息传播路径范围不再受限于时序最短路径,也无需再考虑用路径长度最短还是时间间隔最短定义时序最短路径时序随机游走路径复杂,计算复杂度和时间复杂度高 基于随机游走的时序节点介数[79] Katz中心性基于随机游走的沟通介数和分解介数 时序PageRank分数以及个性化的时序PageRank[24] PageRank 以快照为基本单位,定义节点对间的转移概率,并在此基础上定义时序网络一个周期内的转移矩阵 TempoRank[40] 累积期望中心性[39]、节点传播|获取实时性消息的节点关键程度指标[34] 随机游走路径 在P2P网络中,将消息传播路径分解到时间-空间两个维度上,并利用两个衰减因子分别刻画消息的效用随传播路径长度衰减及随时间推移衰减这两种自然特性 基于传播动力学的识别方法 对动力学敏感的中心性[97] SIR传播模型SI传播模型 基于疾病传播模型可以研究网络的结构特性及组成部分的相对重要性。基于此,结合疾病传播过程的特征提出相应的节点重要性表征指标 将信息传播的动力学过程明显建模为时序网络中的疾病传播模型,简化了时序网络中关键节点研究的过程 受限于传播学模型的设定,可能忽略了实际传播过程中的重要信息 基于机器学习的识别方法 —— 支持向量机SVM[104]决策树[105]梯度下降算法[55] 机器学习方法 1)分类节点以区分关键节点和非关键节点
2)在机器学习方法应用的基础上提出表征节点重要性的指标新方法在旧场景下的新应用,研究前景广。同时,机器学习算法的性能优,对更精准识别关键节点有帮助 现有研究内容较少,缺乏可靠的依据和支撑;机器学习算法的应用解释能力较弱 其他识别方法 —— 研究办公大楼中面对面接触的时序数据以获得关键节点[106] 部门的组织结构 结合数据直接分析识别重要节点 基于具体的情形研究具体的关键节点,针对性强 无法推广到其他不相关的情形 通过属性获得时序社交网络中活跃且有价值的节点的方法[53] 图挖掘序列挖掘 基于社区探测算法选择社区的核心及两社区的桥梁,然后基于序列探测算法划分行为趋势,从而获取活跃有价值的节点 基于信息论的识别有影响力节点的方法[35] 信息论基于熵的中心性 基于如果一个节点连接到更多在后续的快照中有更多邻居的节点,那么该节点可能是一个更重要的传播者 考虑了不同快照中节点影响的关系,是对现有其他研究的补充 计算复杂度大,考虑的网络初始时间具有限定性 1) 网络的时序演化。现有的时序网络多考虑节点和连边随时间的增加和减少,尚未考虑网络结构的巨变,如从星形网络(关键节点最好的识别方法为度中心性)到桥连通网络(关键节点最好的识别方法为介数中心性)的演化。在此情况下,简单的静态图、时间窗图模型、多层图模型或路径流模型不再能概括时序网络模型的演化特征,基于一类模型设计标准一致的关键节点识别方法也难以捕捉到不同时间的关键节点。因此,需要寻找新的网络抽象方法,同时也需要探索可以随网络结构变化而调整的关键节点识别方法。
2) 时序网络中关键节点识别方法的内在关系。基于不同的角度获得了各种关键节点识别方法,但这些方法实际上存在一定的联系,比如前面讨论的基于特征向量的识别方法和基于随机游走的识别方法。因此可以基于多个时序数据集构建不同的时序网络模型,对比分析这些时序识别方法间的联系和区别。
3) 时序网络中节点重要性的定义。相对静态网络中对关键节点识别的各种中心性测度,现有的时序网络中对关键节点的识别方法大多仍然是基于时序网络模型提出的全局时序静态指标,因此忽略了节点的位置和功能随时间而变化的情形;虽然有基于特定时间层的时序指标,但忽略了网络结构随时间变化的情形。而同一类型的时序指标只能探索节点在一个层面的重要性,因此在设计时序网络中的关键节点时,可以同时结合网络结构、节点位置以及节点功能等多方面的影响因素。
4) 时序网络中基于机器学习的关键节点识别方法。随着大数据时代的到来,机器学习由于能从海量数据中挖掘出有价值的信息而逐渐呈现出巨大优势。目前,机器学习方法已被应用于静态网络的关键节点分析并取得了较好的效果,机器学习有望应用于时序网络探索关键节点的识别方法,因此可以从该角度出发进行尝试性探索与应用。
本文研究还得到S-Tech学术支持计划−互联网传播学项目的资助,在此表示感谢。
Identification Methods of Vital Nodes on Temporal Networks
-
摘要: 相对静态网络,时序网络可以更准确地刻画现实网络的动态过程。基于时序网络模型,如何有效地识别重要节点或者评价时序网络中一个节点对其他节点的影响力,已成为时序网络研究领域中的一个亟待解决的问题。该文分别从时序网络拓扑结构和动力学的角度,对现有的时序网络中的关键节点识别方法进行了系统的回顾,详细比较各种方法的计算思路、应用场景和优缺点。最后总结了这一研究方向几个待解决的问题,并指出未来可能的发展方向。Abstract: Comparing with static network, temporal network is more suitable to characterize the dynamic evolution of real systems. It is of great importance to identify vital nodes and evaluate the node influence based on the models of temporal network. From the perspective of the topology and dynamics of temporal networks, we aim to review the recent research progress of identifying vital nodes, summarize and classify relevant identification methods, analyze their advantages and disadvantages, and point out the forefront as well as critical challenges of the field.
-
Key words:
- evaluation index /
- spreading dynamics /
- temporal network /
- topology /
- vital node
-
图 5 基于交互数据拟合SIR传播模型生成的基于明显路径流的时序网络模型[52]
表 1 时序网络中的关键节点识别方法
归类 时序网络中关键
节点识别方法方法示例 基准方法/模型 方法说明 优点 缺点 基于拓扑结构的识别方法 基于度中心性的识别方法 时序度中心性[47] 度中心性 聚焦于时序网络中随时间变化节点度值的波动性 简单直观,时间复杂度低 只能反映节点在整个时间段内的全局局部重要性 时序度中心性偏差值[37] 基于最短路径的识别方法 时序介数中心性[28, 47] 介数中心性 聚焦于重新度量时序网络中的路径、最短路径及距离 计算节点随时间推移的全局重要性,即始点或中介的传播能力 时间复杂度高,不适用大型网络 时序接近中心
性[28, 33, 47, 50]接近中心性 时序覆盖中心性[48] —— 基于K-核分解的识别方法 时序k-shell值[38] K-核值 聚焦于点的时序重要性到边的全局重要性再到点的全局重要性的传递 通过时序网络的分解重构和节点的重要性传递获取在整个时间段内节点的全局重要性 时间复杂度高,只能获得节点的全局重要性 基于特征向量的识别方法 边际节点中心性边际时间层节点中心性节点在特定时间层上的条件中心性[44] 静态网络中基于特征向量的中心性测度,如特征向量中心性PageRank枢纽值与权威值特征因子等 基于时序网络模型在超中心性矩阵中耦合时间层中心性矩阵,再求解主特征向量 获得的往往是对应时间快照上的节点重要性排序以及同一节点不同时间快照上的重要性排序,结果更微观真实 构建的超中心性矩阵需要耦合时间层中心性矩阵,计算复杂度高,且层间的关系定义不明 时序特征向量中心性[45] 基于动力学的识别方法 基于随机游走的识别方法 传播中心性和接收沟通性[78] Katz中心性 基于所提出的任意长度的时序随机游走路径,以及静态网络中的Katz中心性计算方法计,从而计算时序网络中的沟通性矩阵 1.通过对随机游走的时序定义以及对时间或空间维度信息衰减程度的表征,更真实刻画了网络中消息传递的路径,所得的节点重要性的评判结果更真实
2.相对基于最短路径的识别方法,基于随机游走的识别方法所考虑的信息传播路径范围不再受限于时序最短路径,也无需再考虑用路径长度最短还是时间间隔最短定义时序最短路径时序随机游走路径复杂,计算复杂度和时间复杂度高 基于随机游走的时序节点介数[79] Katz中心性基于随机游走的沟通介数和分解介数 时序PageRank分数以及个性化的时序PageRank[24] PageRank 以快照为基本单位,定义节点对间的转移概率,并在此基础上定义时序网络一个周期内的转移矩阵 TempoRank[40] 累积期望中心性[39]、节点传播|获取实时性消息的节点关键程度指标[34] 随机游走路径 在P2P网络中,将消息传播路径分解到时间-空间两个维度上,并利用两个衰减因子分别刻画消息的效用随传播路径长度衰减及随时间推移衰减这两种自然特性 基于传播动力学的识别方法 对动力学敏感的中心性[97] SIR传播模型SI传播模型 基于疾病传播模型可以研究网络的结构特性及组成部分的相对重要性。基于此,结合疾病传播过程的特征提出相应的节点重要性表征指标 将信息传播的动力学过程明显建模为时序网络中的疾病传播模型,简化了时序网络中关键节点研究的过程 受限于传播学模型的设定,可能忽略了实际传播过程中的重要信息 基于机器学习的识别方法 —— 支持向量机SVM[104]决策树[105]梯度下降算法[55] 机器学习方法 1)分类节点以区分关键节点和非关键节点
2)在机器学习方法应用的基础上提出表征节点重要性的指标新方法在旧场景下的新应用,研究前景广。同时,机器学习算法的性能优,对更精准识别关键节点有帮助 现有研究内容较少,缺乏可靠的依据和支撑;机器学习算法的应用解释能力较弱 其他识别方法 —— 研究办公大楼中面对面接触的时序数据以获得关键节点[106] 部门的组织结构 结合数据直接分析识别重要节点 基于具体的情形研究具体的关键节点,针对性强 无法推广到其他不相关的情形 通过属性获得时序社交网络中活跃且有价值的节点的方法[53] 图挖掘序列挖掘 基于社区探测算法选择社区的核心及两社区的桥梁,然后基于序列探测算法划分行为趋势,从而获取活跃有价值的节点 基于信息论的识别有影响力节点的方法[35] 信息论基于熵的中心性 基于如果一个节点连接到更多在后续的快照中有更多邻居的节点,那么该节点可能是一个更重要的传播者 考虑了不同快照中节点影响的关系,是对现有其他研究的补充 计算复杂度大,考虑的网络初始时间具有限定性 -
[1] HOLME P, SARAMÄKI J. Temporal networks[J]. Physics Reports, 2012, 519(3): 97-125. doi: 10.1016/j.physrep.2012.03.001 [2] HOLME P. Modern temporal network theory: A colloquium[J]. The European Physical Journal B, 2015, 88(9): 234. doi: 10.1140/epjb/e2015-60657-4 [3] KOSTAKOS V. Temporal graphs[J]. Physica A, 2009, 388(6): 1007-1023. doi: 10.1016/j.physa.2008.11.021 [4] LI A, CORNELIUS S, LIU Y Y, et al. The fundamental advantages of temporal networks[J]. Science, 2017, 358(6366): 1042-1046. doi: 10.1126/science.aai7488 [5] LIAO Hao, MARIANI M S, MEDO M, et al. Ranking in evolving complex networks[J]. Physics Reports, 2017, 689: 1-54. doi: 10.1016/j.physrep.2017.05.001 [6] EAGLE N, PENTLAND A. Reality mining: Sensing complex social systems[J]. Personal and Ubiquitous Computing, 2006, 10(4): 255-268. doi: 10.1007/s00779-005-0046-3 [7] ROCHA L E C, LILJEROS F, HOLME P. Information dynamics shape the networks of Internet-mediated prostitution[J]. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(13): 5706-5711. doi: 10.1073/pnas.0914080107 [8] ISELLA L, STEHLÉ J, BARRAT A, et al. What's in a crowd? Analysis of face-to-face behavioral networks[J]. Journal of Theoretical Biology, 2011, 271(1): 166-180. doi: 10.1016/j.jtbi.2010.11.033 [9] STEHLÉ J, VOIRIN N, BARRAT A, et al. High-resolution measurements of face-to-face contact patterns in a primary school[J]. PLOS ONE, 2011, 6(8): e23176. doi: 10.1371/journal.pone.0023176 [10] VAN DEN BROECK W, QUAGGIOTTO M, ISELLA L, et al. The making of sixty-nine days of close encounters at the science gallery[J]. Leonardo, 2012, 45(3): 285-285. doi: 10.1162/LEON_a_00377 [11] VANHEMS P, BARRAT A, CATTUTO C, et al. Estimating potential infection transmission routes in hospital wards using wearable proximity sensors[J]. PLOS ONE, 2013, 8(9): e73970. doi: 10.1371/journal.pone.0073970 [12] LÜ Lin-yuan, CHEN Duan-bing, REN Xiao-long, et al. Vital nodes identification in complex networks[J]. Physics Reports, 2016, 650: 1-63. doi: 10.1016/j.physrep.2016.06.007 [13] 刘建国, 任卓明, 郭强, 等. 复杂网络中节点重要性排序的研究进展[J]. 物理学报, 2013, 62(17): 9-18. LIU Jian-guo, REN Zhuo-ming, GUO Qiang, et al. Node importance ranking of complex networks[J]. Acta Phys Sin, 2013, 62(17): 9-18. [14] 任晓龙, 吕琳媛. 网络重要节点排序方法综述[J]. 科学通报, 2014, 59(13): 1175-1197. doi: 10.1360/972013-1280 REN Xiao-long, LÜ Lin-yuan. Review of ranking nodes in complex networks[J]. Chinese Science Bulletin, 2014, 59(13): 1175-1197. doi: 10.1360/972013-1280 [15] CHEN Duan-bing, LÜ Lin-yuan, SHANG Ming-sheng, et al. Identifying influential nodes in complex networks[J]. Physica A, 2012, 391(4): 1777-1787. doi: 10.1016/j.physa.2011.09.017 [16] CHEN Duan-bing, GAO Hui, LÜ Lin-yuan, et al. Identifying influential nodes in large-scale directed networks: The role of clustering[J]. PLOS ONE, 2013, 8(10): e77455. doi: 10.1371/journal.pone.0077455 [17] LI Qian, ZHOU Tao, LÜ Lin-yuan, et al. Identifying influential spreaders by weighted LeaderRank[J]. Physica A, 2014, 404: 47-55. doi: 10.1016/j.physa.2014.02.041 [18] LÜ Lin-yuan, ZHOU Tao, ZHANG Qian-ming, et al. The H-index of a network node and its relation to degree and coreness[J]. Nature Communications, 2016, 7: 10168. doi: 10.1038/ncomms10168 [19] JI Sheng-gong, LÜ Lin-yuan, YEUNG C H, et al. Effective spreading from multiple leaders identified by percolation in the susceptible-infected-recovered (SIR) model[J]. New Journal of Physics, 2017, 19(7): 073020. doi: 10.1088/1367-2630/aa76b0 [20] ZHOU Fang, LÜ Lin-yuan, MARIANI M S. Fast influencers in complex networks[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 74: 69-83. doi: 10.1016/j.cnsns.2019.01.032 [21] GUNTURI V M V, SHEKHAR S, JOSEPH K, et al. Scalable computational techniques for centrality metrics on temporally detailed social network[J]. Machine Learning, 2017, 106(8): 1133-1169. doi: 10.1007/s10994-016-5583-7 [22] KEMPE D, KLEINBERG J, KUMAR A. Connectivity and inference problems for temporal networks[J]. Journal of Computer and System Sciences, 2002, 64(4): 820-842. doi: 10.1006/jcss.2002.1829 [23] KOSSINETS G, KLEINBERG J, WATTS D. The structure of information pathways in a social communication network[J]. KDD, 2008, 31(1): 435-443. [24] ROZENSHTEIN P, GIONIS A. Temporal PageRank[C]//Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2016. Cham: Springer Press, 2016: 674-689. [25] FERREIRA A. Building a reference combinatorial model for MANETs[J]. IEEE Network, 2004, 18(5): 24-29. doi: 10.1109/MNET.2004.1337732 [26] MICHAIL O. An introduction to temporal graphs: An algorithmic perspective[M]. Cham: Springer International Publishing, 2015. [27] TANG J K, MUSOLESI M, MASCOLO C, et al. Temporal distance metrics for social network analysis[C]//Proceedings of the 2nd ACM workshop on Online social networks. New York: ACM Press, 2009: 31-36. [28] TANG J K, MUSOLESI M, MASCOLO C, et al. Analysing information flows and key mediators through temporal centrality metrics[C]//Proceedings of the 3rd Workshop on Social Network Systems. New York: ACM Press, 2010: 3-9. [29] TANG J K, SCELLATO S, MUSOLESI M, et al. Small-world behavior in time-varying graphs[J]. Physical Review E, 2010, 81(5): 055101. doi: 10.1103/PhysRevE.81.055101 [30] NICOSIA V, TANG J, MASCOLO C, et al. Graph metrics for temporal networks[M]. Berlin, Heidelberg: Springer, 2013. [31] STARNINI M, MACHENS A, CATTUTO C, et al. Immunization strategies for epidemic processes in time-varying contact networks[J]. Journal of Theoretical Biology, 2013, 337(47): 89-100. [32] 朱义鑫, 张凤荔, 秦志光. 时序网络演化速度对传播的影响分析[J]. 计算机应用, 2014, 34(11): 3184-3187. ZHU Yi-xin, ZHANG Feng-li, QIN Zhi-guang. Effects analysis of network evolution speed on propagation in temporal networks[J]. Journal of Computer Applications, 2014, 34(11): 3184-3187. [33] MAGNIEN C, TARISSAN F. Time evolution of the importance of nodes in dynamic networks[C]//Proceedings of the 2015 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining 2015. New York: ACM Press, 2015: 1200-1207. [34] 白宇清, 李海健, 蔡青松. 移动P2P社会网络中关键节点发现方法[J]. 计算机科学与探索, 2016, 10(3): 350-362. BAI Yu-qing, LI Hai-jian, CAI Qing-song. Discovering Key Nodes in Mobile P2P Social Networks[J]. Journal of Frontiers of Computer Science and Technology, 2016, 10(3): 350-362. [35] LUO Liang, TAO Li, XU Hong-yi, et al. An information theory based approach for identifying influential spreaders in temporal networks[C]//Cyberspace Safety and Security. CSS 2017. Cham: Springer, 2017: 477-484. [36] OGURA M, PRECIADO V M. Katz centrality of markovian temporal networks: Analysis and optimization[J]. 2017 American Control Conference (ACC), 2017(1): 5001-5006. [37] WANG Zhi-qiang, PEI Xu-bing, WANG Yan-bo, et al. Ranking the key nodes with temporal degree deviation centrality on complex networks[C]//The 29th Chinese Control And Decision Conference (CCDC). Chongqing: IEEE, 2017: 1484-1489. [38] YE Zhang-hui, ZHAN Xiu-xiu, ZHOU Yin-zuo, et al. Identifying vital nodes on temporal networks: An edge-based K-Shell decomposition[C]//The 36th Chinese Control Conference (CCC). Dalian: IEEE, 2017: 1402-1407. [39] LERMAN K, GHOSH R, KANG J. Centrality metric for dynamic networks[J]. KDD, 2010, 33(8): 70-77. [40] ROCHA L E C, MASUDA N. Random walk centrality for temporal networks[J]. New Journal of Physics, 2014, 16(6): 063023. doi: 10.1088/1367-2630/16/6/063023 [41] KRINGS G, KARSAI M, BERNHARDSSON S, et al. Effects of time window size and placement on the structure of an aggregated communication network[J]. EPJ Data Science, 2012, 1(1): 4. doi: 10.1140/epjds4 [42] RIBEIRO B, PERRA N, BARONCHELLI A. Quantifying the effect of temporal resolution in time-varying network[J]. Computer Science, 2012, 3(10): 3006. [43] WEHMUTH K, ZIVIANI A, FLEURY E. A unifying model for representing time-varying graphs[C]//2015 IEEE International Conference on Data Science and Advanced Analytics (DSAA). Paris: IEEE, 2015: 1-10. [44] TAYLOR D, MYERS S A, CLAUSET A, et al. Eigenvector-based centrality measures for temporal networks[J]. Multiscale Modeling & Simulation, 2015, 15(1): 537-574. [45] 杨剑楠, 刘建国, 郭强. 基于层间相似性的时序网络节点重要性研究[J]. 物理学报, 2018, 67(4): 279-286. YANG Jian-nan, LIU Jian-guo, GUO Qiang. Node importance idenfication for temporal network based on inter-layer similarity[J]. Acta Phys Sin, 2018, 67(4): 279-286. [46] 郭强, 殷冉冉, 刘建国. 基于TOPSIS的时序网络节点重要性研究[J]. 电子科技大学学报, 2019, 48(2): 1-6. doi: 10.3969/j.issn.1001-0548.2019.01.001 GUO Qiang, YIN Ran-ran, LIU Jian-guo. Node importance identification for temporal networks via the TOPSIS method[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(2): 1-6. doi: 10.3969/j.issn.1001-0548.2019.01.001 [47] KIM H, ANDERSON R J. Temporal node centrality in complex networks[J]. Physical Review E, 2012, 85(2): 026107. doi: 10.1103/PhysRevE.85.026107 [48] TAKAGUCHI T, YANO Y, YOSHIDA Y. Coverage centralities for temporal networks[J]. European Physical Journal B, 2016, 89(2): 1-11. [49] BRAMSON A, VANDERMARLIERE B. Benchmarking measures of network influence[J]. Scientific Reports, 2016, 6(1): 34052. doi: 10.1038/srep34052 [50] PAN R K, SARAMAKI J. Path lengths, correlations, and centrality in temporal networks[J]. Physical Review E, 2011, 84(1): 016105. doi: 10.1103/PhysRevE.84.016105 [51] DARST R K, GRANELL C, ARENAS A, et al. Detection of timescales in evolving complex systems[J]. Scientific Reports, 2016, 6(1): 39713. doi: 10.1038/srep39713 [52] ESTRADA E. Communicability in temporal networks[J]. Physical Review E, 2013, 88(4): 042811. doi: 10.1103/PhysRevE.88.042811 [53] QIU D, LI H, LI Y. Identification of active valuable nodes in temporal online social network with attributes[J]. International Journal of Information Technology Decision Making, 2014, 13(4): 839-864. doi: 10.1142/S0219622014500618 [54] SCHOLTES I, WIDER N, GARAS A. Higher-Order aggregate networks in the analysis of temporal networks: path structures and centralities[J]. European Physical Journal B, 2016, 89(3): 61. doi: 10.1140/epjb/e2016-60663-0 [55] ABBAS K, SHANG M, ABBASI A, et al. Popularity and novelty dynamics in evolving networks[J]. Scientific Reports, 2018, 8(1): 6332. doi: 10.1038/s41598-018-24456-2 [56] NEWMAN M. Networks: An introduction[M]. Cambridge: Cambridge University Press, 2010. [57] FREEMAN L C. A set of measures of centrality based on betweenness[J]. Sociometry, 1977, 40(1): 35-41. doi: 10.2307/3033543 [58] SABIDUSSI G. The centrality index of a graph[J]. Psychometrika, 1966, 31(4): 581-603. doi: 10.1007/BF02289527 [59] KITSAK M, GALLOS L K, HAVLIN S, et al. Identification of influential spreaders in complex networks[J]. Nature Physics, 2010, 6(11): 888-893. doi: 10.1038/nphys1746 [60] EISLER Z, BARTOS I, KERTÉSZ J. Fluctuation scaling in complex systems: Taylor's law and beyond[J]. Advances in Physics, 2008, 57(1): 89-142. doi: 10.1080/00018730801893043 [61] WU Huan-huan, CHENG J, HUANG S, et al. Path problems in temporal graphs[J]. Proceedings of the VLDB Endowment, 2014, 7(9): 721-732. doi: 10.14778/2732939.2732945 [62] TANG J K, LEONTIADIS I, SCELLATO S, et al. Applications of temporal graph metrics to real-world networks[M]. Berlin, Heidelberg: Springer, 2013. [63] TANG J K, MASCOLO C, MUSOLESI M, et al. Exploiting temporal complex network metrics in mobile malware containment[J]. World of Wireless Mobile Multimedia Networks, 2011(1): 1-9. [64] QU Cun-quan, ZHAN Xiu-xiu, WANG Guang-hui, et al. Temporal information gathering process for node ranking in time-varying networks[J]. Chaos, 2019, 29(3): 033116. doi: 10.1063/1.5086059 [65] GARAS A, SCHWEITZER F, HAVLIN S. A k-shell decomposition method for weighted networks[J]. New Journal of Physics, 2012, 14(8): 083030. doi: 10.1088/1367-2630/14/8/083030 [66] LIU Jian-guo, REN Zhuo-ming, GUO Qiang. Ranking the spreading influence in complex networks[J]. Physica A, 2013, 392(18): 4154-4159. doi: 10.1016/j.physa.2013.04.037 [67] 任卓明, 刘建国, 邵凤, 等. 复杂网络中最小K-核节点的传播能力分析[J]. 物理学报, 2013, 62(10): 474-479. REN Zhuo-ming, LIU Jian-guo, SHAO Feng, et al. Analysis of the spreading influence of the nodes with minimum K-shell value in complex networks[J]. Acta Phys Sin, 2013, 62(10): 474-479. [68] STEPHENSON K, ZELEN M. Rethinking centrality: Methods and examples[J]. Social Networks, 1989, 11(1): 1-37. doi: 10.1016/0378-8733(89)90016-6 [69] BRIN S, PAGE L. The anatomy of a large-scale hypertextual Web search engine[J]. Computer Networks and ISDN Systems, 1998, 30(1-7): 107-117. doi: 10.1016/S0169-7552(98)00110-X [70] GLEICH D F. PageRank beyond the web[J]. Siam Review, 2015, 57(3): 321-363. doi: 10.1137/140976649 [71] KLEINBERG J M. Authoritative sources in a hyperlinked environment[J]. Journal of the ACM, 1999, 46(5): 604-632. doi: 10.1145/324133.324140 [72] BERGSTROM C T, WISEMAN W M A. The eigenfactor metrics[J]. Journal of Neuroscience, 2008, 28(45): 11433-11434. doi: 10.1523/JNEUROSCI.0003-08.2008 [73] KATZ L, POWELL J H. A proposed index of the conformity of one sociometric measurement to another[J]. Psychometrika, 1953, 18(3): 249-256. doi: 10.1007/BF02289063 [74] BRYAN K, LEISE T L. The $25,000,000,000 eigenvector: The linear algebra behind google[J]. Siam Review, 2006, 48(3): 569-581. doi: 10.1137/050623280 [75] LÜ Lin-yuan, ZHANG Yi-cheng, YEUNG C H, et al. Leaders in social networks, the delicious case[J]. PLOS ONE, 2011, 6(6): e21202. doi: 10.1371/journal.pone.0021202 [76] ACER U G, DRINEAS P, ABOUZEID A A. Random walks in time-graphs[C]//Proceedings of the Second International Workshop on Mobile Opportunistic Networking. New York: ACM, 2010: 93-100. [77] MICHELE S, ANDREA B, ALAIN B, et al. Random walks on temporal networks[J]. Physical Review E, 2012, 85(5): 056115. doi: 10.1103/PhysRevE.85.056115 [78] KATZ L. A new status index derived from sociometric analysis[J]. Psychometrika, 1953, 18(1): 39-43. doi: 10.1007/BF02289026 [79] PETER G, PARSONS M C, HIGHAM D J, et al. Communicability across evolving networks[J]. Physical Review E, 2011, 83(4): 046120. doi: 10.1103/PhysRevE.83.046120 [80] ALSAYED A, HIGHAM D J. Betweenness in time dependent networks[J]. Chaos Solitons & Fractals, 2015, 72: 35-48. [81] ESTRADA E, HIGHAM D J, HATANO N. Communicability betweenness in complex networks[J]. Physica A, 2009, 388(5): 764-774. doi: 10.1016/j.physa.2008.11.011 [82] ESTRADA E, J. HIGHAM D. Network properties revealed through matrix functions[J]. Siam Review, 2010, 52(4): 696-714. doi: 10.1137/090761070 [83] CHEN Shu-hua, YAN Han, LI Jian-cheng, et al. Improvement of PageRank algorithm: An authoritative and temporal based approach[C]//IEEE Conference Anthology. [S.L.]: IEEE, 2013: 1-4. [84] BERBERICH K, VAZIRGIANNIS M, WEIKUM G. Time-aware authority ranking[J]. Internet Mathematics, 2005, 2(3): 301-332. doi: 10.1080/15427951.2005.10129110 [85] MANASKASEMSAK B. Time-weighted web authoritative ranking[J]. Information Retrieval, 2011, 14(2): 133-157. doi: 10.1007/s10791-010-9138-4 [86] BAEZA-YATES R, SAINT-JEAN F, CASTILLO C. Web structure, dynamics and page quality[C]//String Processing and Information Retrieval. SPIRE 2002. Berlin, Herdelberg: Springer, 2002: 117-130. [87] YU P S, LI Xin, LIU Bing. Adding the temporal dimension to search-a case study in publication search[C]//The 2005 IEEE/WIC/ACM International Conference on Web Intelligence (WI'05). Compiegne: IEEE, 2005: 543-549. [88] FIALA D. Time-aware PageRank for bibliographic networks[J]. Journal of Informetrics, 2012, 6(3): 370-388. doi: 10.1016/j.joi.2012.02.002 [89] JUNIOR P S P, GONCALVES M A, LAENDER A H F, et al. Time-aware ranking in sport social networks[J]. Journal of Information Data Management, 2012, 3(3): 195-210. [90] HU Wei-shu, ZOU Hai-tao, GONG Zhi-guo. Temporal PageRank on social networks[C]//Web Information Systems Engineering-WISE 2015. Cham: Springer, 2015: 262-276. [91] PASTORSATORRAS R, CASTELLANO C, VAN MIEGHEM P, et al. Epidemic processes in complex networks[J]. Reviews of Modern Physics, 2015, 87(3): 925-979. doi: 10.1103/RevModPhys.87.925 [92] 张子柯. 在线社交网络信息传播机制与动力学研究综述[J]. 情报学报, 2017, 36(4): 422-431. doi: 10.3772/j.issn.1000-0135.2017.04.011 ZHANG Zi-ke. Mechanisms and dynamics of information spreading on online social networks: A state-of-the-art survey[J]. Journal of the China Society for Scientific and Technical Information, 2017, 36(4): 422-431. doi: 10.3772/j.issn.1000-0135.2017.04.011 [93] COHEN R, HAVLIN S. Complex networks: Structure, robustness and function[M]. Cambridge: Cambridge University Press, 2010. [94] BARRAT A, BARTHLEMY M, VESPIGNANI A. Dynamical processes on complex networks[M]. Cambridge: Cambridge University Press, 2008. [95] BUTTS C T. Revisiting the foundations of network analysis[J]. Science, 2009, 325(5939): 414-416. doi: 10.1126/science.1171022 [96] GONCALVES B, PERRA N. Social phenomena from sata analysis to models[M]. Berline, Heidelberg: Springer, 2015. [97] LIU Jian-guo, LIN Jian-hong, GUO Qiang, et al. Locating influential nodes via dynamics-sensitive centrality[J]. Scientific Reports, 2016, 6(1): 21380. doi: 10.1038/srep21380 [98] HUANG Da-wen, YU Zu-guo. Dynamic-sensitive centrality of nodes in temporal networks[J]. Scientific Reports, 2017, 7(1): 41454. doi: 10.1038/srep41454 [99] SILVA T C, ZHAO L. Machine learning in complex networks[M]. Cham: Springer International Publishing, 2016. [100] WANG Fei-fan, ZHANG Bai-hai, CHAI Sen-chun, et al. An extreme learning machine-based community detection algorithm in complex networks[J]. Complexity, 2018(1): 1-10. [101] ZENG Zheng-zhong, CHEN Ke-jia, ZHANG Shao-bo, et al. A link prediction approach using semi-supervised learning in dynamic networks[C]//2013 Sixth International Conference on Advanced Computational Intelligence (ICACI). Hangzhou: IEEE, 2013: 276-280. [102] HISANO R. Semi-supervised graph embedding approach to dynamic link prediction[C]//Complex Networks IX. CompleNet 2018. Cham: Springer, 2018: 109-121. [103] TORRES D D E, ROCCO S C M. A comparative study for assessing the reliability of complex networks using rules extracted from different machine learning approaches[C]//AI 2005: Advances in Artificial Intelligence. Berlin, Heidelberg: Springer, 2005: 954-958. [104] SCHIMBINSCHI F, NGUYEN X V, BAILEY J, et al. Traffic forecasting in complex urban networks: leveraging big data and machine learning[C]//2015 IEEE International Conference on Big Data. Santa Clara: IEEE, 2015: 1019-1024. [105] 林国强, 赵毅鸣, 况青作, 等. 基于复杂网络和机器学习的P2P用户违约预测[J]. 北京师范大学学报(自然科学版), 2017, 53(1): 24-27, 29. LIN Guo-qiang, ZHAO Yi-ming, KUANG Qing-zuo, et al. Predicting bad P2P loans with machine learning and complex network algorithm[J]. Journal of Beijing Normal University(Natural Science), 2017, 53(1): 24-27, 29. [106] FANG X, HU P J. Top persuader prediction for social networks[J]. Management Information Systems Quarterly, 2018, 42(1): 63-82. doi: 10.25300/MISQ/2018/13211 [107] GÉNOIS M, VESTERGAARD C L, FOURNET J, et al. Data on face-to-face contacts in an office building suggest a low-cost vaccination strategy based on community linkers[J]. Network Science, 2015, 3(3): 326-347. doi: 10.1017/nws.2015.10 [108] YER S, KILLINGBACK T, SUNDARAM B, et al. Attack robustness and centrality of complex networks[J]. PLOS ONE, 2013, 8(4): e59613. doi: 10.1371/journal.pone.0059613 [109] Cheng Xue-qi, Ren Fu-xin, Shen Hua-wei, et al. Bridgeness: A local index on edge significance in maintaining global connectivity[J]. Journal of Statistical Mechanics: Theory and Experiment, 2010(10): P10011. doi: 10.1088/1742-5468/2010/10/P10011 [110] LATORA V, MARCHIORI M. Efficient behavior of small-world networks[J]. Physical Review Letters, 2001, 87(19): 198701. doi: 10.1103/PhysRevLett.87.198701 [111] COSTA E C, VIEIRA A B, WEHMUTH K, et al. Time centrality in dynamic complex networks[J]. Advances in Complex Systems, 2015, 18: 1550023. doi: 10.1142/S021952591550023X [112] HOLME P. Temporal network structures controlling disease spreading[J]. Physical Review E, 2016, 94(2): 022305. [113] KENDALL M G. A new measure of rank correlation[J]. Biometrika, 1938, 30(1-2): 81-93. doi: 10.1093/biomet/30.1-2.81 [114] FIELLER E C, HARTLEY H O, PEARSON E S. Tests for Rank Correlation Coefficients[J]. Biometrika, 1957, 44(3-4): 470-481. doi: 10.1093/biomet/44.3-4.470 -


 ISSN
ISSN 



 下载:
下载: