ISSN 
下载:
-
近年来，随着对复杂网络科学认识的深入，科学家们发现很多的真实系统都可以用多层网络结构进行更精确的描述。例如，人际关系网中的线下朋友关系以及线上朋友关系等；不同运输工具(航空网、铁路网和公路网)构成的交通网络等。因此关于多层网络的结构及动力学的研究已经成为网络科学领域的一个研究热点和重点[1-11]。
传染性疾病的爆发会引发相关的信息通过人群内部、新闻媒介以及在线社交网络等多种渠道传播，而人们获得该信息后会警觉且采取一定的预防措施自我保护，从而对疾病传播产生深远的影响。已有学者在研究传染病动力学的时候开始从不同角度考虑信息因素的影响，如：个体根据对疾病信息的了解程度来调整与外界的接触情况[12]，个体行为方式的改变[13]，人群内部、新闻媒介以及在线社交网络传播信息对疾病传播的影响[14]；文献[15]基于传统的“S(susceptible)-I(infected)-S(susceptible)”疾病传播模型，考虑了节点会通过邻居的感染状况而出现警惕状态，而警觉态易感者被感染的概率显然和易感态不同，提出了S(susceptible)-A(aware)-I(infected)-S(susceptible)”模型，但其模型的研究局限于单个网络，没有考虑警惕信息的传播问题；文献[16]又研究了信息传播对疾病传播的影响，并找出在不同网络拓扑下最理想的信息传播机制；文献[17]在双层网络中研究疾病和信息两类传播动力学的相互作用，揭示信息传播对疾病传播及传播阈值的影响；文献[18]进一步研究了一种局部警觉控制传染模型(LACS)，其中当节点的警惕邻居数目与信息层节点度的比值达到局部警惕率或已被疾病感染，才能变成警惕态传播警惕信息；文献[19]研究了双层网络上具有自激发和扩散机制的警觉行为对传播动力学的影响；文献[20]考虑了双层网络上个体的异质性对警惕信息传播动力学的影响等。
之前基于双层网络对疾病传播与警觉意识扩散的研究多存在一个普遍性假设：在同一时刻警觉意识先传播，疾病后传播。虽然信息传播途径广一些，传播也更加便利一些，但是并非所有情况都如此。比如有些疾病虽然已经在人群中传播，但由于疾病的外部表现不容易被发现或者危险性没有引起充分注意，可能导致警觉不能快速传播。再比如，对于有些疾病而言，感染疾病的人不太愿意告诉他人自己的得病情况(比如性病等)，因此警觉也不能快速传播。故与之前的研究都不同，本文摒弃之前的假设，而是认为警觉意识与疾病的传播是不分先后次序的，进而比较两种机制对传播阈值和传播范围的影响。
-
文献[17]考虑到疾病的爆发会引发警觉意识的传播，而且两种传播动力学的传播载体往往不同，因此基于双层网络提出经典的UAU-SIS模型。
双层网络是指警觉意识传播的虚拟层和疾病传播的接触层，它们的邻接矩阵分别为
${({{\rm{a}}_{ij}})_{N \times N}}$ 和${({{\rm{b}}_{ij}})_{N \times N}}$ ，其中$N$ 表示网络的节点数。类似于传统的SIS疾病传播过程，虚拟层进行警觉意识传播U(unaware)-A(aware)-U(unawre)。按照对现存疾病风险是否有警觉意识，节点分为无警觉态(U)和警觉态(A)。虚拟层中处于警觉态的节点以概率$\lambda $ 扩散警觉行为，而且无警觉的节点一旦感染自动变为警觉态。处于警觉态的节点又会以概率$\delta $ 忘记此信息，再次成为无警觉态。接触层是疾病传播过程(SIS)，节点分为易感态(S)和感染态(I)。记无警觉态被感染率为
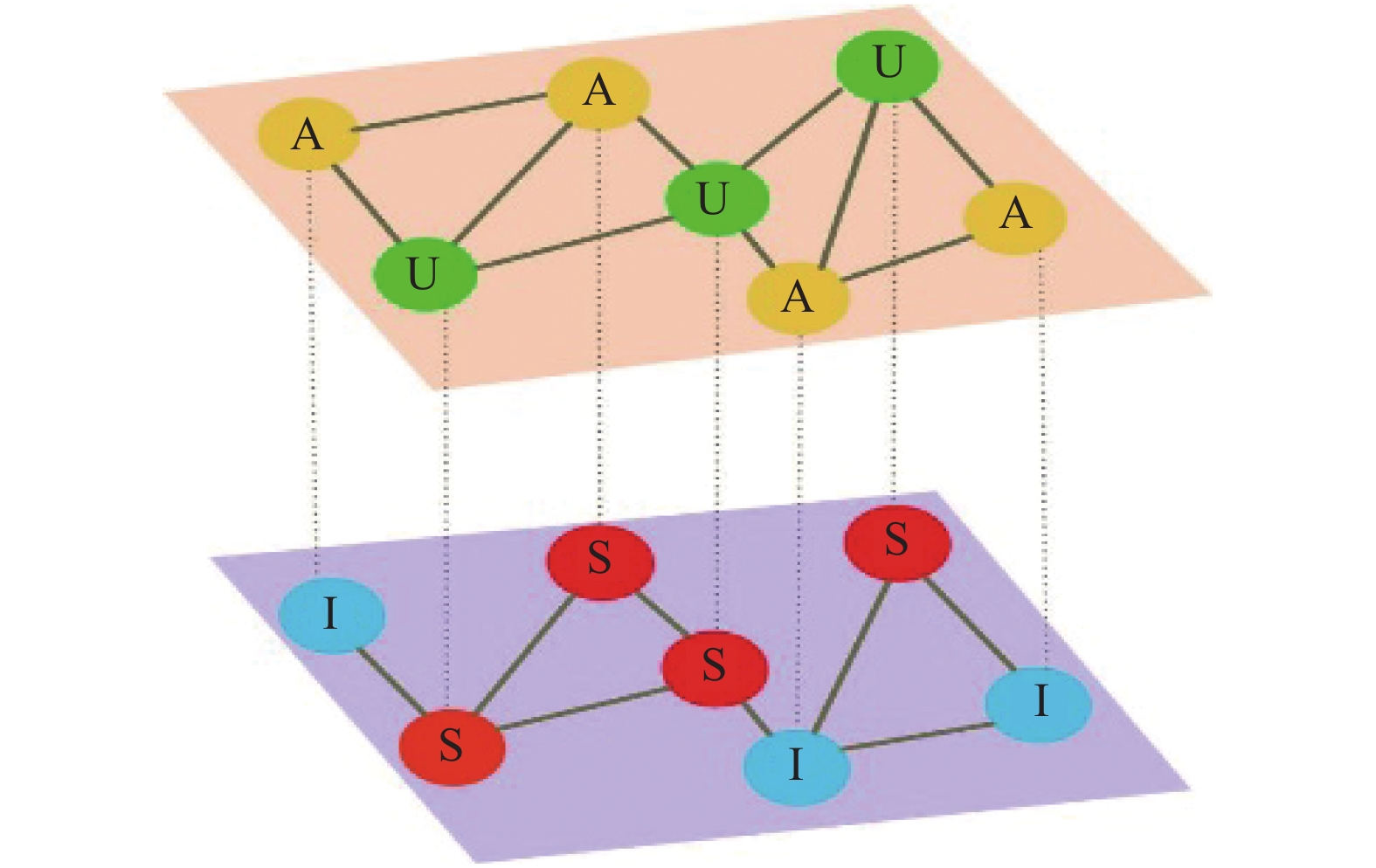
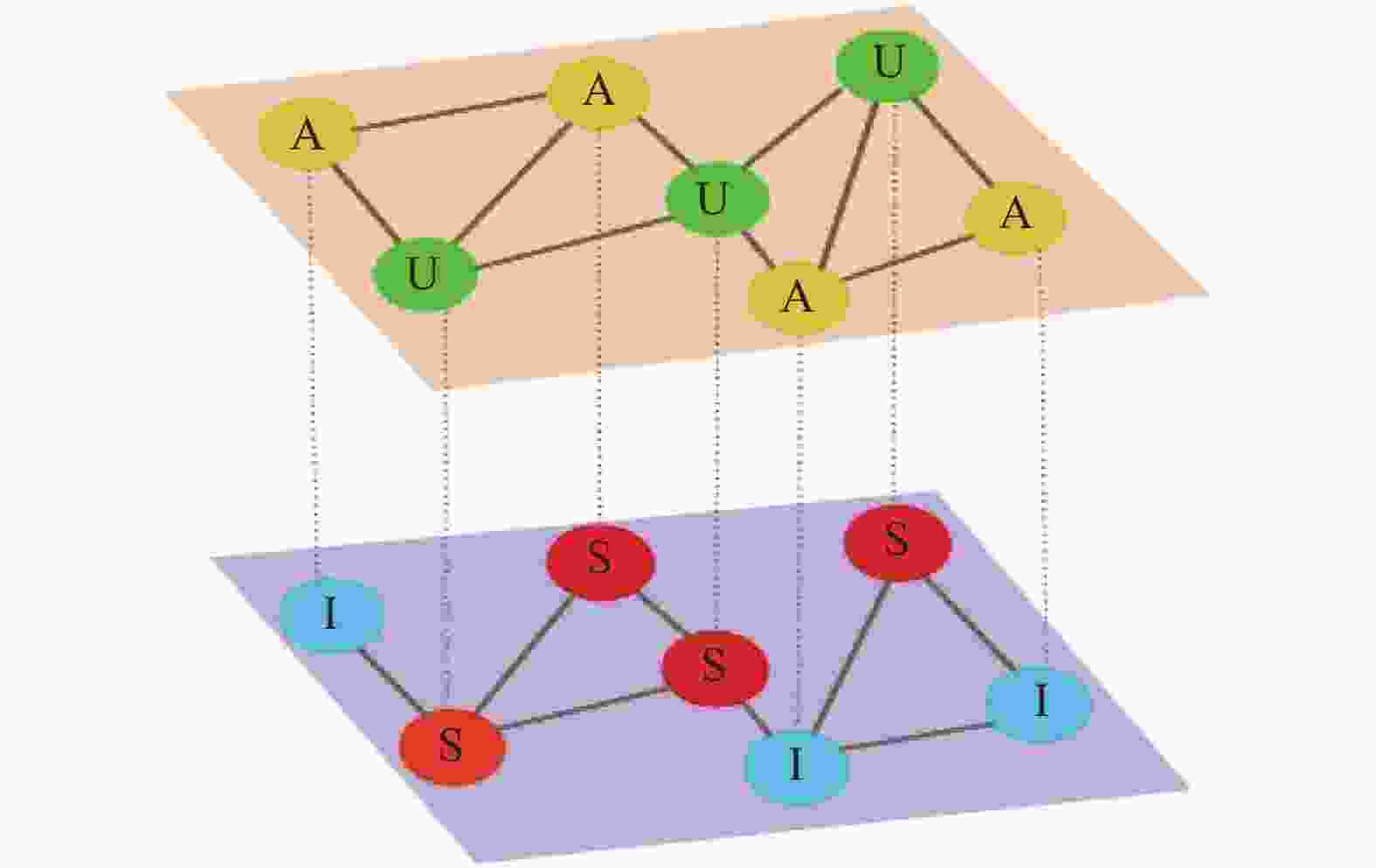
${\beta ^{\rm U}}$ ，警觉态感染率为${\beta ^{\rm A}}$ ，感染恢复率为$\mu $ 。因为无警觉态节点不知道疾病的信息，因而没有采取相应的保护措施，而警觉态节点了解到疾病的风险，通过一些自我保护措施(如减少外出、加强卫生等)，所以减少了被感染的几率。假设警觉态通过一个因子$\gamma $ 来降低感染，记$\,{\beta ^{\rm A}}$ =$\gamma $ $\,{\beta ^{\rm U}}$ ，其中$0 \leqslant \gamma \leqslant 1$ 。这种双层网络上两种动力学相互作用的示意图如图1所示，上层是警觉意识传播的虚拟层，节点分为无警觉态(U)和警觉态(A)；下层是疾病传播的接触层，节点分为易感态(S)和感染态(I)。
图 1 双层网络上两种动力学相互作用的示意图
-
根据UAU-SIS模型，节点处于3种不同状态：无警觉且易感态(US)，警觉且易感态(AS)，警觉且感染态(AI)；未警觉的感染态，即UI态是不存在的，因为假设节点一旦感染就立即变为警觉态，所以UI对应于AI态。在时刻t，每个节点
$i$ 都以一个确定的概率处于这3种状态之一，分别表示为$p_i^{\rm {US}}({\rm{t}})$ 、$p_i^{\rm {AS}}({\rm{t}})$ 和$p_i^{\rm {AI}}(t)$ 。假设没有动力的相关性[16]，同时记处于U态的节点$i$ 未被警觉的概率为${\gamma _i}(t)$ ，处于U态的节点$i$ 未被感染的概率为$q_i^{\rm U}(t)$ ，处于A态的节点$i$ 未被感染的概率为$q_i^{\rm A}(t)$ ，则：$${\gamma _i}(t) = \prod\limits_j {(1 - {a_{ji}}p_j^{\rm A}(t)\lambda )}$$ (1) $$q_i^{\rm U}(t) = \prod\limits_j {(1 - {b_{ji}}p_j^{\rm I}(t){\beta ^{\rm U}})}$$ (2) $$q_i^{\rm A}(t) = \prod\limits_j {(1 - {b_{ji}}p_j^{\rm I}(t){\beta ^{\rm A}})}$$ (3) 下面将分析双层网络中信息与疾病的传播次序性对传播动力学的影响。
-
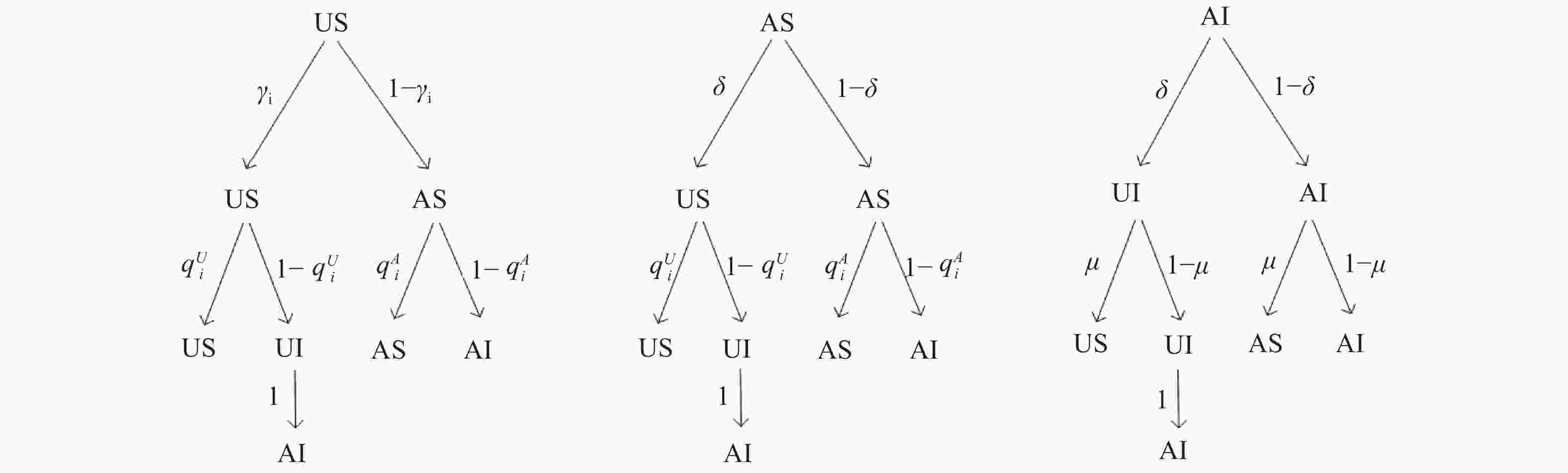
文献[17]在进行理论分析时，假设警觉意识的传播优先于疾病的传播(简称为ordered model)，即在同一时刻警觉意识先传播，疾病后传播，从而有每个节点可能处的状态以及概率转化图如图2所示，其中
${\gamma _i}(t)$ 为处于U态的节点$i$ 未警觉的概率，$q_i^{\rm U}(t)$ 为处于U态的节点$i$ 未被感染的概率，$q_i^{\rm A}(t)$ 为处于A态的节点$i$ 未被感染的概率,$\delta $ 为警觉信息恢复率，$\mu $ 为感染恢复率。列出如下马尔可夫方程：$$ \begin{split} & p_i^{\rm {US}}(t + 1) = p_i^{\rm {US}}(t){\gamma _i}(t)q_i^{\rm U}(t) + p_i^{\rm {AS}}(t)\delta q_i^{\rm U}(t) + p_i^{\rm {AI}}(t)\delta \mu \\ &\qquad\qquad p_i^{\rm {AS}}(t + 1) = p_i^{\rm {US}}(t)\left[ {1 - {\gamma _i}(t)} \right]q_i^{\rm A}(t) +\\ &\qquad\qquad p_i^{\rm {AS}}(t)(1 - \delta )q_i^{\rm A}(t) + p_i^{\rm {AI}}(t)(1 - \delta )\mu \end{split} $$ $$\begin{split} &\;\; p_i^{\rm {AI}}(t + 1) = p_i^{\rm {US}}(t)\left\{ {[ {1 - {\gamma _i}(t)} ][ {1 - q_i^{\rm A}(t)} ] +}\right. \\ &\qquad\;\; \left.{{\gamma _i}(t)[ {1 - q_i^{\rm U}(t)} ]} \right\} + p_i^{\rm {AS}}(t)\\ & {\left\{ {\delta [ {1 - q_i^{\rm U}(t)} ] + (1 - \delta )[ {1 - q_i^{\rm A}(t)} ]} \right\} + p_i^{\rm {AI}}(t)(1 - \mu )} \end{split} $$ 
图 2 ordered model中每个时步节点各状态的概率转变树图
通过理论分析，得出传播阈值
$\,\beta _c^U = \dfrac{\mu }{{{ \wedge _{\max }}({ H})}}$ ，其中矩阵H的元素为${h_{ji}} = \left( {1 - (1 - \gamma )p_i^{\rm A}} \right){b_{ji}}$ 。故传播阈值受到双层网络结构、警觉意识的传播率等因素的影响。 -
文献[17]的研究以及基于此工作的推广都存在一个假设：在同一时刻警觉意识先传播，疾病后传播。虽然信息传播途径更便利一些，但在有些情况下，这种人为规定警觉传播的优先性是欠妥的，因为只有疾病发生了，警觉意识才会传播，另外，当人们没有充分意识到疾病的风险时，警觉意识的传播也未必快于疾病传播。故与之前的研究都不同，本文摒弃之前的假设，而是认为警觉意识与疾病的传播是不分先后次序的，提出一种不考虑传播次序的模型(简称为concurrent model)。
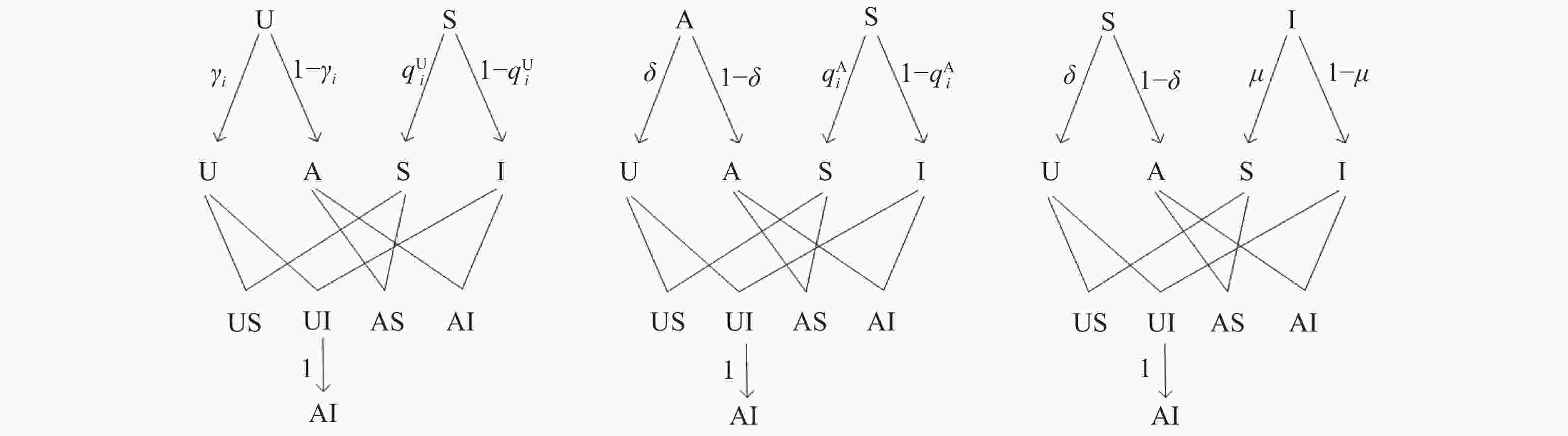
对于concurrent model模型，图3刻画了每个节点可能处的状态以及概率转化图，其中
${\gamma _i}(t)$ 为处于U态的节点$i$ 未警觉的概率，$q_i^{\rm U}(t)$ 为处于U态的节点$i$ 未被感染的概率，$q_i^{\rm A}(t)$ 为处于A态的节点$i$ 未被感染的概率，$\delta $ 为警觉信息恢复率，$\mu $ 为感染恢复率。
图 3 concurrent model中每个时步节点各状态的概率转变树图
根据图3的概率转移图并结合马尔可夫链方法[17-19]，可以列出如下马尔可夫方程：
$$p_i^{\rm {US}}(t + 1) = p_i^{\rm {US}}(t){\gamma _i}(t)q_i^{\rm U}(t) + + p_i^{\rm {AS}}(t)\delta q_i^{\rm A}(t) + p_i^{\rm {AI}}(t)\delta \mu $$ (4) $$ \begin{split} & p_i^{\rm {AS}}(t + 1) = p_i^{\rm {US}}(t)\left[ {1 - {\gamma _i}(t)} \right]q_i^{\rm U}(t) +\\ & p_i^{\rm {AS}}(t)(1 - \delta )q_i^{\rm A}(t) + p_i^{\rm {AI}}(t)(1 - \delta )\mu \end{split} $$ (5) $$ \begin{split} & p_i^{\rm {AI}}(t + 1) = p_i^{\rm {US}}(t)\left[ {1 - q_i^{\rm U}(t)} \right] + + p_i^{\rm {AS}}(t)\times\\ &\qquad\; \left[ {1 - q_i^{\rm A}(t)} \right] + p_i^{\rm {AI}}(t)(1 - \mu ) \end{split} $$ (6) 这里
$p_i^{\rm {US}}(t) + p_i^{\rm {AS}}(t) + p_i^{\rm {AI}}(t) \equiv 1$ 。$p_j^{\rm A} = p_j^{\rm {AS}} + p_j^{\rm {AI}},$ $p_j^{\rm I} = p_j^{\rm {AI}}$ 。当系统稳定时，$p_i^{\rm {US}}(t + 1) = p_i^{\rm {US}}(t) = p_i^{\rm {US}}$ ，$p_i^{\rm {AS}}(t + 1) = p_i^{\rm {AS}}(t){\rm{ = }}p_i^{\rm {AS}}$ ，$p_i^{\rm {AI}}(t + 1) = p_i^{\rm {AI}}(t){\rm{ = }}p_i^{\rm {AI}}$ 。传播阈值决定疾病的爆发或灭亡，因此分析各参数对阈值的影响十分重要。在阈值附近，节点被感染的概率很低，使得
$p_i^{\rm I} = {\varepsilon _i} \ll {\rm{1}}$ ，因此有$q_i^{\rm A} \approx 1 - {\beta ^{\rm A}}$ $\displaystyle\sum {\left( {{b_{ji}}{\varepsilon _j}} \right)} $ 和$q_i^{\rm U} \approx 1 - {\beta ^U}\displaystyle\sum {\left( {{{\rm{b}}_{ji}}{\varepsilon _j}} \right)} $ 。假定$p_i^{\rm I} = {\varepsilon _i} \to {\rm{0}}$ ，进一步近似$q_i^{\rm A} \approx 1$ 和$q_i^{\rm U} \approx 1$ ，代入并整理式(4)和式(5)得到：$$ p_i^{\rm {US}} = p_i^{\rm {US}}{\gamma _i} + p_i^{\rm {AS}}\delta $$ (7) $$ p_i^{\rm {AS}} = p_i^{\rm {US}}(1 - {\gamma _i}) + p_i^{\rm {AS}}(1 - \delta ) $$ (8) 联合式(6)～式(8)，则得一个更简单的式子：
$$\mu {\varepsilon _i} = (p_i^{\rm {US}}{\beta ^{\rm U}} + p_i^{\rm {AS}}{\beta ^{\rm A}})\sum {{b_{ji}}{\varepsilon _j}} $$ (9) 又因为
$\,{\beta ^{\rm A}} = \gamma {\beta ^{\rm U}}$ ，$p_i^{\rm U} = p_i^{\rm {US}} $ ，$p_i^{\rm A} = p_i^{\rm {AS}} \!+\! p_i^{\rm {AI}} \!\approx p_i^{\rm {AS}} $ ，$p_i^{\rm I} = {\varepsilon _i} \ll {\rm{1}}$ ，则式(9)整理成：$$\sum\limits_{} {\left[ {\left( {1 - (1 - \gamma )p_i^{\rm A}} \right){b_{ji}} - \frac{\mu }{{{\beta ^U}}}{\delta _{ji}}} \right]} {\varepsilon _j} = 0$$ (10) 式中，当
$i = j$ 时，${\delta _{ij}} = 1$ ；否则为0。定义矩阵H，其元素为
${h_{ji}} = \left( {1 - (1 - \gamma )p_i^{\rm A}} \right){b_{ji}}$ 。式(10)即为：$$H\varepsilon = \frac{\mu }{{{\beta ^{\rm U}}}}\varepsilon $$ (11) 式中，
$\varepsilon = {({\varepsilon _1},{\varepsilon _2},\cdots,{\varepsilon _N})^{\rm T}}$ 。式(11)的非平凡解就是矩阵H对应于特征值为$\dfrac{\mu }{{{\beta ^{\rm U}}}}$ 的特征向量，记${ \wedge _{\max }}({ H})$ 为矩阵H的最大特征值，则感染阈值就可以写成：$$\beta _c^{\rm U} = \frac{\mu }{{{ \wedge _{\max }}({ H})}}$$ (12) 从式(10)～式(12)可以得出，传播阈值依赖于实际接触层的网络结构
${({{{b}}_{ij}})_{N \times N}}$ 、参数$\gamma $ 以及警觉密度${\rho ^{\rm A}}$ 。其中${\rho ^{\rm A}}$ 是由信息层网络结构、传播率$\lambda $ 以及恢复率$\delta $ 等进一步确定的。故传播阈值受到双层网络结构、警觉意识的传播率等因素的影响。同时研究结果表明，两种模型得到的传播阈值是相同的。 -
为验证本文的理论结果，建立一个节点数为2 000、度分布为p(k)～k−2.5的配置网络为接触层
${({{\rm{b}}_{ij}})_{N \times N}}$ ，在接触层上增加800条随机边(无重边)得到虚拟接触层${({{\rm{a}}_{ij}})_{N \times N}}$ 。首先，将无序的马尔可夫链方法(MMCA)和数值模拟(MC)的结果进行比较，如图4所示，其中初始感染种子为0.2，$\lambda {\rm{ = 0}}{\rm{.15}}$ ，$\delta {\rm{ = 0}}{\rm{.6}}$ ，$\mu {\rm{ = 0}}{\rm{.4}}$ 。从图4可以发现两者拟合很好，进而验证了本文基于MMCA的理论分析的有效性。
图 4 马尔可夫链方法(MMCA)和数值模拟(MC)方法的对比
图 5 在不同的警惕恢复率
$\delta $ 和疾病恢复率$\mu $ 下，${\beta _c}$ 随$\lambda $ 的变化图然后，根据式(12)作出疾病传播阈值
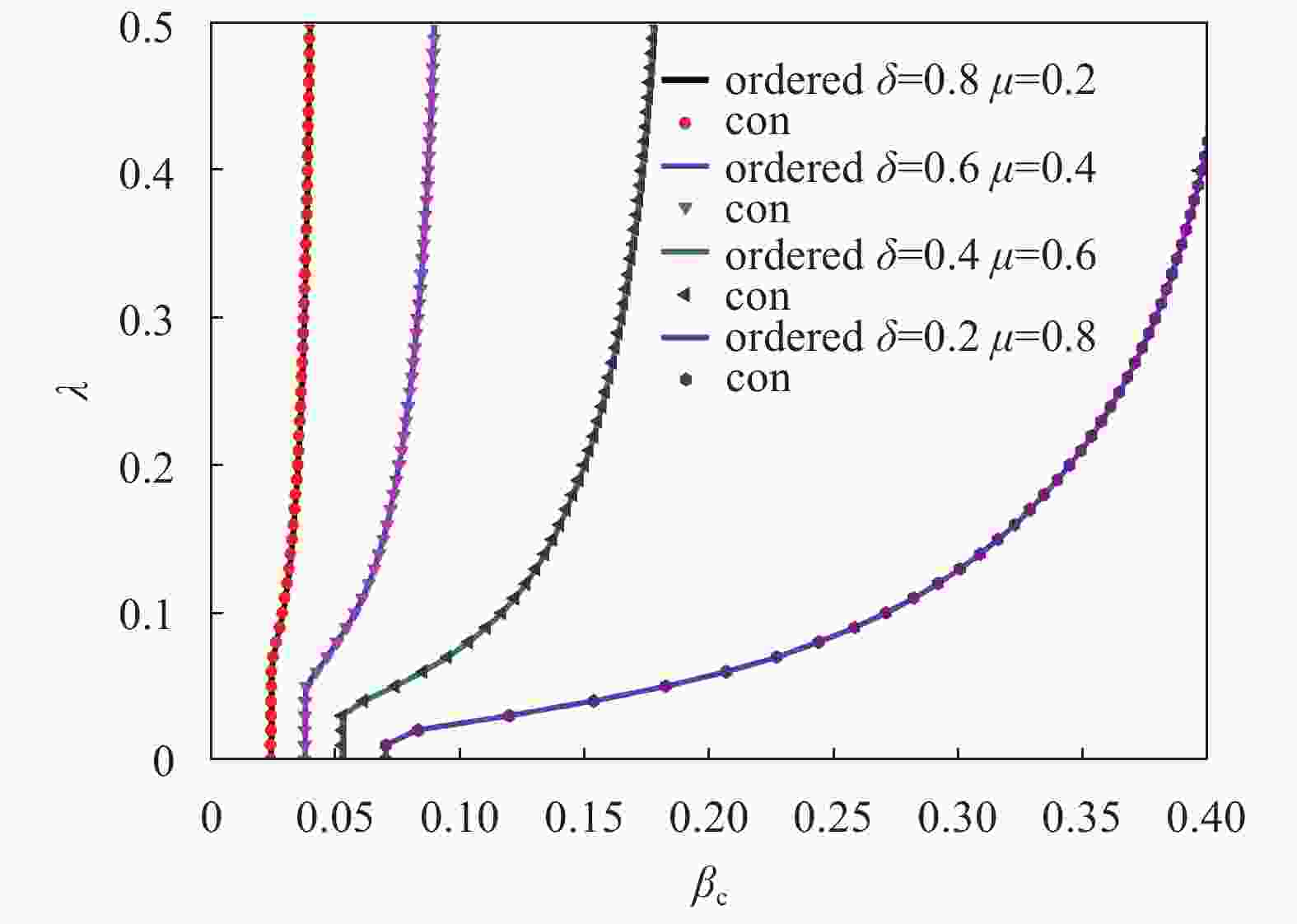
${\beta _c}$ 随信息层传播率$\lambda $ 的变化图(本文的结果都是基于无序的MMCA得到的)，从图5可以发现，在不同的警惕恢复率$\delta $ 和信息恢复率$\mu $ 下，$\,{\beta _c}$ 随$\lambda $ 的变化曲线不同；当信息层传播率$\lambda $ 大于一定值时(信息传播阈值)，疾病传播阈值${\beta _c}$ 随着信息层传播率$\lambda $ 的增大而增大；从而说明疾病传播阈值${\beta _c}$ 不仅依赖于实际接触层的拓扑结构还依赖于虚拟信息层警觉信息的扩散；同时，在相同的警惕恢复率$\delta $ 和信息恢复率$\mu $ 下，无序模型(con)和有序模型(ordered)的疾病传播阈值${\beta _c}$ 相同，说明传播的次序不影响疾病传播阈值。这是因为，虽然$\,{\beta _c}$ 依赖于虚拟层的动力系统，尤其是变量$p_i^{\rm A}$ ，但在阈值附近，可认为下层疾病没有传播，只有信息层扩散，从而$p_i^{\rm A}$ 相同，故传播阈值${\beta _c}$ 相同。进一步给出在不同的警觉意识传播率
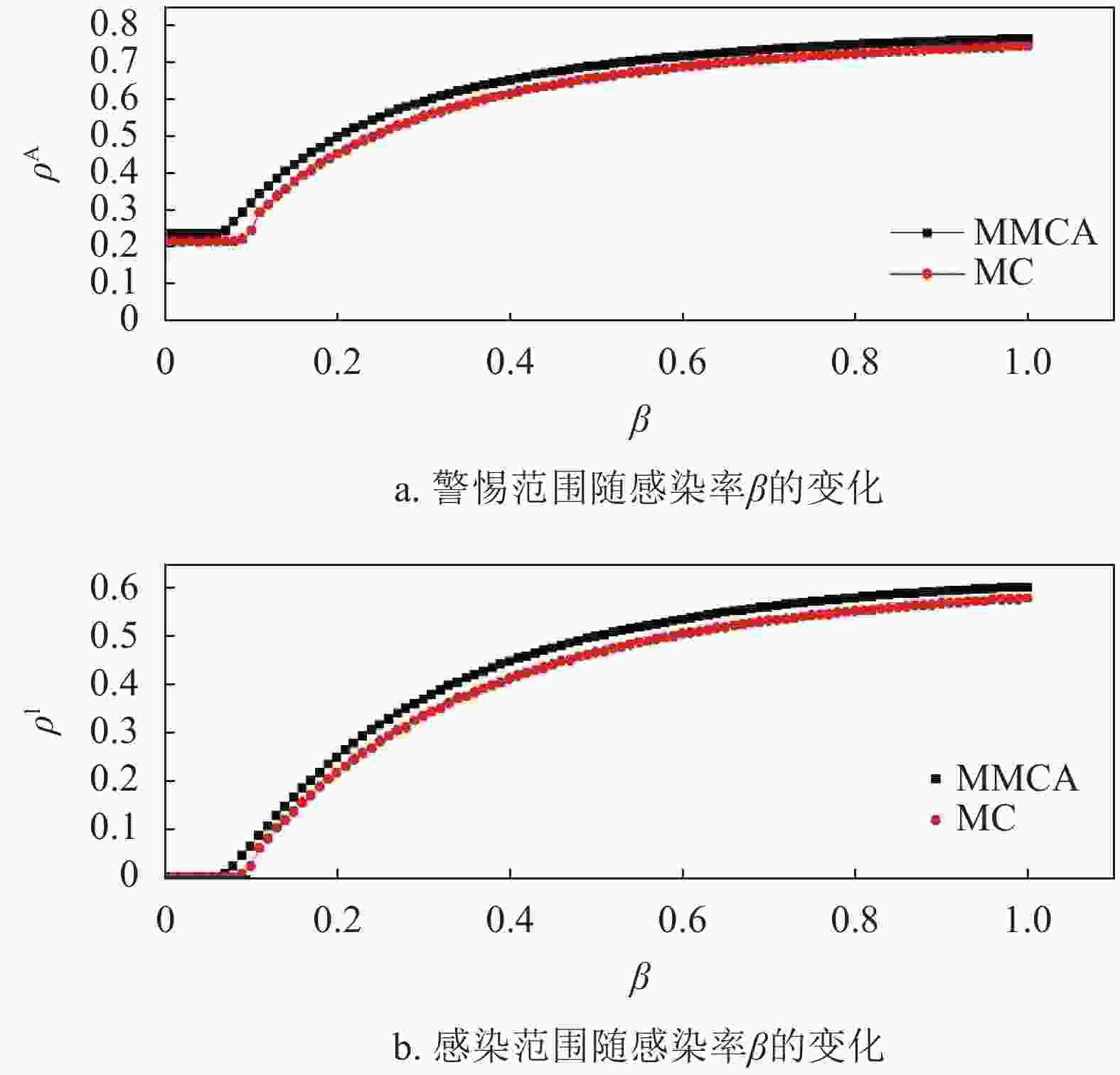
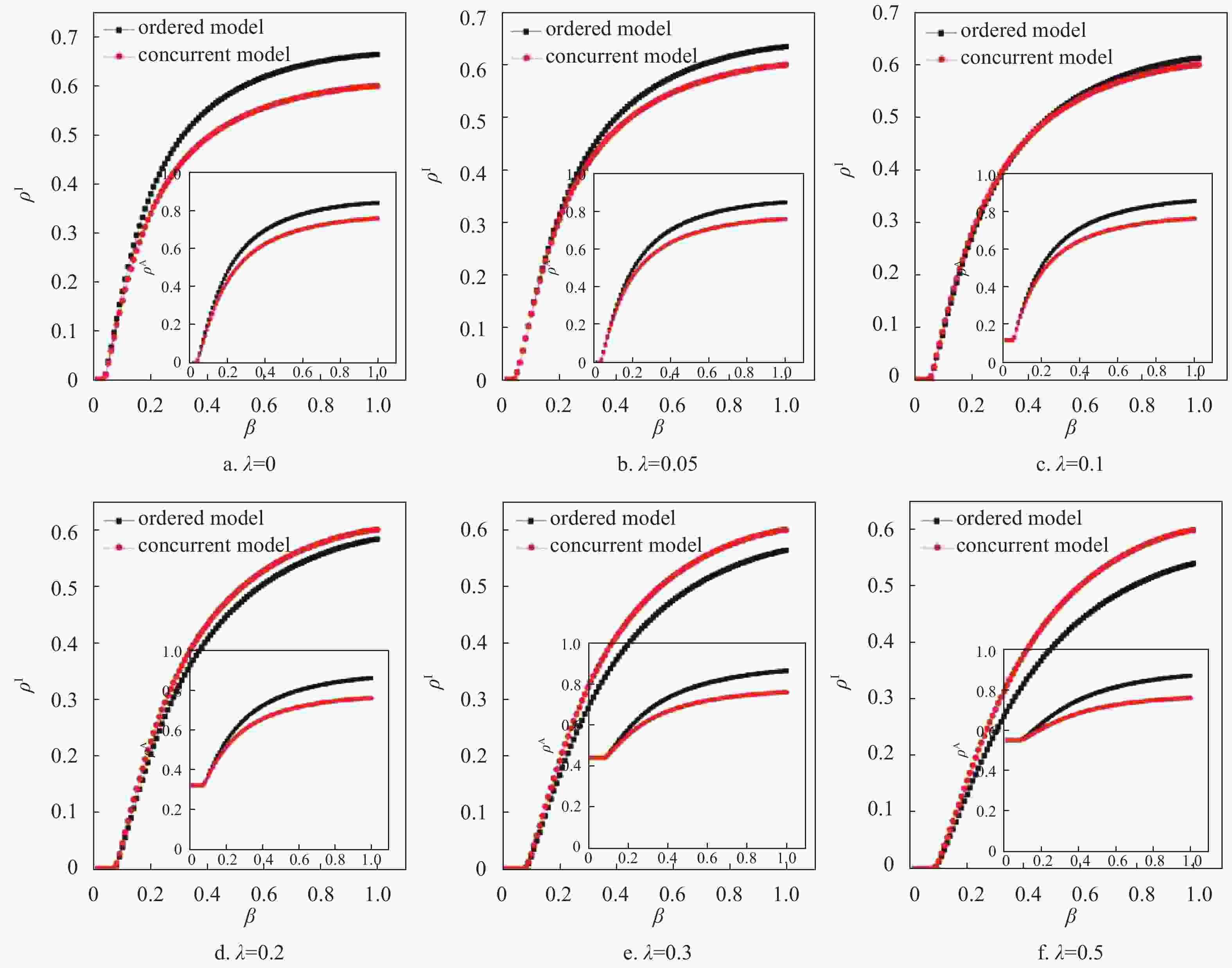
$\lambda $ 下，感染范围$\,{\rho ^{\rm I}}$ 随着感染传播率$\,\beta $ 的变化图，并在每个子图中插入对应的警觉意识传播范围$\,{\rho ^{\rm A}}$ 随感染传播率$\,\beta $ 的变化，如图6所示，其中初始感染种子为0.2，$\delta {\rm{ = 0}}{\rm{.6}}$ ，$\mu {\rm{ = 0}}{\rm{.4}}$ 。可以发现：1) 当警觉意识传播率$\lambda $ 固定时，随着感染率$\,\beta $ 增大，感染范围${\rho ^{\rm I}}$ 显然会增大，而感染者会自动成为警惕态促进警觉信息传播，从而警觉范围$\,{\rho ^{\rm A}}$ 增大；2) 当警觉意识传播率$\lambda $ 较小的时候，从图6a、6b和6c中可以观察到，无序模型(con)对应的感染范围小于有序模型(ordered)对应的感染范围，但是随着警觉意识传播率的增加，从图6d、6e和6f中可以观察到，结果会发生反转，即无序性模型对应的疾病感染传范围会逐渐大于有序性模型；3) 有序模型(ordered)对应的警觉传播范围$\,{\rho ^{\rm A}}$ 总是大于无序模型(con)对应的警觉传播范围，对于这种现象需要分为两种情况加以解释：当$\lambda $ 较小的时候，节点的警觉态主要是因为被感染自动变为警觉态，而有序模型(con)感染范围较大一些，所以其警觉范围也更大一些；当$\lambda $ 较大的时候，节点大部分处于警觉状态，因为有序模型先在虚拟层进行警觉意识传播，故会有一部分节点先恢复成未警觉状态，增加了这部分节点的感染率，节点感染会立马警觉，从而导致恢复成未警觉状态节点在同一个时刻更容易变为警觉态，所以有序模型的警觉范围依然大于无序的。
图 6 在不同的警觉意识传播率
$\lambda $ 下，con与ordered中感染范围$\,{\rho ^{\rm I}}$ 随$\,\beta $ 的变化图图6的结论3)表明：无论
$\lambda $ 取何值，有序模型对应的警觉传播范围$\,{\rho ^{\rm A}}$ 总是大于无序模型对应的警觉传播范围。但是结论2)却表明：$\lambda $ 较小的时候有序模型的感染范围$\,{\rho ^{\rm I}}$ 会较大一些；相反的，当$\lambda $ 较大的时候有序模型的感染范围$\,{\rho ^{\rm I}}$ 会较小一些。即，不能简单地认为警觉传播范围大的模型对应的疾病传播范围一定更小。这是因为：当$\lambda $ 较小时，虽然有序模型对应的警觉传播范围大于无序模型对应的警觉传播范围，但是此时两者的警觉范围都比较小。对于有序模型而言，当进行疾病传播的时候，上一步的警觉者还没有通过虚拟层大范围扩散就又变回为未警觉态，从而导致有序模型对应的感染范围更广；当$\lambda $ 较大时，两个模型对应的警觉范围都很大，而有序模型先通过虚拟层进行警觉意识传播，故会进一步增大警觉传播范围，而警觉态节点会降低自身的感染率，从而有序模型对应的感染范围就会较小一些。为了进一步验证上述结论是否具有一般性，本文用ER随机网络生成双层网络模型[21]，首先生成一个节点数为2 000、平均度
$\left\langle k \right\rangle = 5$ 的随机网络，作为接触层${({{{b}}_{ij}})_{N \times N}}$ ，然后在接触层上增加800条随机边(无重边)得到虚拟接触层${({{{a}}_{ij}})_{N \times N}}$ 。进一步给出在不同的警觉意识传播率$\lambda $ 下，感染范围$\,{\rho ^{\rm I}}$ 随着感染传播率$\beta $ 的变化图，并在每个子图中插入对应的警觉意识传播范围${\rho ^{\rm A}}$ 随着感染传播率$\beta $ 的变化图，如图7所示，其中初始感染种子为0.2，$\delta {\rm{ = 0}}{\rm{.6}}$ ，$\mu {\rm{ = 0}}{\rm{.4}}$ 。可以发现，图7和图6具有相同的现象，从而验证了结论的普适性。
图 7 在不同的警觉意识传播率
$\lambda $ 下，con与ordered中感染范围$\,{\rho ^{\rm I}}$ 随$\,\beta $ 的变化图 -
本文提出不考虑传播次序的模型，即警觉意识与疾病同时传播。通过理论分析和数值模拟发现，感染范围和阈值不仅依赖于双层网络结构而且受警觉信息传播的影响。与之前的模型进行对比发现：信息与疾病的传播次序不影响疾病的传播阈值，但会影响两种传播的动力学传播范围。虽然无序模型对应的警觉传播范围总是小于有序模型对应的警觉传播范围，但却会对疾病传播范围有截然不同的影响：在警觉意识传播率较小的时候，有序模型导致警觉态节点没有大范围传播就变为未警觉态，从而导致疾病传播范围增加；而当警觉意识传播率较大的时候，有序模型保证警觉意识在虚拟层更大范围扩散，从而更有效控制疾病在物理层的扩散。本文的研究工作表明：当基于双层网络研究疾病和意识传播耦合作用时需要根据问题背景设定相应的模型并进行分析，否则可能会导致错误的结果。同时本文的研究工作也丰富了多层网络动力学的研究结果。
本文的研究工作得到安徽科技学院人才引进项目(100005)的支持，在此深表感谢！
Effects of the Order of Awareness Diffusion and Disease Propagation on the Spreading Dynamics
-
摘要: 近年来，基于双层网络研究疾病传播与警觉传播的相互作用已引起广泛关注。在该模型框架下，疾病通过物理接触网络传播，而有关疾病的警觉信息则通过虚拟接触网络传播，两个网络具有相同的节点，但对应的连边不同。已有的模型在进行理论分析时，多假设警觉意识的传播先于疾病的传播(ordered model)，考虑到在真实情况下，疾病传播和警觉意识的传播难以区分先后顺序，因此该文提出了一种不考虑传播次序的模型(concurrent model)。通过研究发现，两种模型给出相同的疾病爆发阈值，但却给出不同的传播范围，当警觉意识传播率较小的时候，无序模型对应的感染范围会小于有序模型对应的感染范围，但是随着警觉意识传播率的增加，结果会发生反转，即无序性模型会导致疾病的感染范围大于有序性模型。Abstract: Recently, studies on the interaction between disease transmission and awareness transmission based on two-layer networks have attracted much attention. Within such a framework, infectious disease is propagated through physical contact networks, while the diffusion of awareness is transmitted through virtual contact network. Moreover, the nodes on two layers are the same, but the edges connecting nodes in the two layers are different. Most of the existing models assume that the diffusion of awareness precedes the spread of disease (hereinafter referred to as ordered model). In real cases, it is difficult to distinguish the order of disease transmission from that of awareness diffusion, thus, this paper proposes a model without considering the order of two spreading processions (concurrent model for short). We find that the two models yield the same epidemic threshold, but have different influence on the spreading sizes. When the transmission rate of awareness is low, the epidemic size of concurrent model is smaller than that of ordered model. However, with the increase of the transmission rate of awareness, the result is reversed, that is, the epidemic size of the concurrent model is larger than that of ordered model.
-
Key words:
- awareness diffusion /
- epidemic threshold /
- infectious diseases /
- two-layer networks
-
[1] GÓMEZ-GARDENES J, REINARES I, ARENAS A, et al. Evolution of cooperation in multiplex networks[J]. Scientific Reports, 2012, 2: 620. doi: 10.1038/srep00620 [2] BIANCONI G. Statistical mechanics of multiplex networks: Entropy and overlap[J]. Physical Review E, 2013, 87(6): 062806. doi: 10.1103/PhysRevE.87.062806 [3] GRANELL C, GÓMEZ S, ARENAS A. Competing spreading processes on multiplex networks: Awareness and epidemics[J]. Physical Review E, 2014, 90(1): 012808. doi: 10.1103/PhysRevE.90.012808 [4] NIE Xiao-yu, TANG Ming, ZOU Yong, et al. The impact of heterogeneous response on coupled spreading dynamics in multiplex networks[J]. Physica A: Statistical Mechanics and its Applications, 2017, 484: 225-232. doi: 10.1016/j.physa.2017.04.140 [5] ZHOU Yin-zuo, ZHOU Jie, CHEN Guan-rong, et al. Effective degree theory for awareness and epidemic spreading on multiple networks[J]. New Journal of Physics, 2019, 21(3): 035002. doi: 10.1088/1367-2630/ab0458 [6] 吴桐雨, 王健. 基于多层复杂网络的物流枢纽城市多尺度分析及发育评价[J]. 交通运输系统工程与信息, 2019, 19(1): 33-39. WU Tong-yu, WANG Jian. Multi-scale analysis and development evaluation of logistics hub cities based on multi-layer[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(1): 33-39. [7] 孙晓璇, 吴晔, 冯鑫, 等. 高铁-普铁的实证双层网络结构与鲁棒性分析[J]. 电子科技大学学报, 2019, 48(2): 315-320. SUN Xiao-xuan, WU Ye, FENG Xin, et al. Structure characteristics and robustness analysis of multi-layer network of high speed railway and ordinary railway[J]. Journal of University of Electronic Science and Technology of China, 2019, 48(2): 315-320. [8] 张欣. 多层复杂网络理论研究进展: 概念、理论和数据[J]. 复杂系统与复杂性科学, 2015, 12(2): 103-107. ZHANG Xin. Multilayer networks science: Concepts, theories and data[J]. Complex Systems and Complexity Science, 2015, 12(2): 103-107. [9] GOMEZ S, DIAZ-GUILERA A, GOMEZ-GARDEÑES J, et al. Diffusion dynamics on multiplex networks[J]. Physical Review Letters, 2013, 110(2): 028701. doi: 10.1103/PhysRevLett.110.028701 [10] 唐明, 崔爱香, 龚凯. 关注耦合网络及其传播动力学研究[J]. 复杂系统与复杂性科学, 2011, 8(2): 87-91. doi: 10.3969/j.issn.1672-3813.2011.02.012 TANG Ming, CUI Ai-xiang, GONG Kai. On spreading dynamics on coupled networks[J]. Complex Systems and Complexity Science, 2011, 8(2): 87-91. doi: 10.3969/j.issn.1672-3813.2011.02.012 [11] 刘权辉, 王伟, 唐明. 多层耦合网络传播综述[J]. 复杂系统与复杂性科学, 2016, 13(1): 48-57. LIU Quan-hui, WANG Wei, TANG Ming. The review of spreading dynamics on multilayer coupled networks[J]. Complex Systems and Complexity Science, 2016, 13(1): 48-57. [12] ZHANG Hai-feng, SMALL M, FU Xin-chu, et al. Modeling the influence of information on the coevolution of contact networks and the dynamics of infectious diseases[J]. Physica D: Nonlinear Phenomena, 2012, 241(18): 1512-1517. doi: 10.1016/j.physd.2012.05.011 [13] 张海峰, 张文耀, 孙桂全, 等. 信息的滞后性诱导传染病的周期爆发[J]. 中国科学: 物理学, 力学, 天文学, 2012, 42(6): 631-638. doi: 10.1360/132011-240 ZHANG Hai-feng, ZHANG Wen-yao, SUN Gui-quan, et al. Time-delayed information can induce the periodic outbreaks of infectious diseases(in Chinese)[J]. Sci Sin-Phys Mech Astron, 2012, 42(6): 631-638. doi: 10.1360/132011-240 [14] WANG Yi, CAO Jin-de, JIN Zhen, et al. Impact of media coverage on epidemic spreading in complex networks[J]. Physica A: Statistical Mechanics and its Applications, 2013, 392(23): 5824-5835. doi: 10.1016/j.physa.2013.07.067 [15] SAHNEH F D, SCOGLIO C. Epidemic spread in human networks[C]//2011 50th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC). [S.l.]: IEEE, 2011: 3008-3013. [16] SAHNEH F D, SCOGLIO C M. Optimal information dissemination in epidemic networks[C]//2012 51st IEEE Annual Conference on Decision and Control (CDC). [S.l.]: IEEE, 2012: 1657-1662. [17] GRANELL C, GÓMEZ S, ARENAS A. Dynamical interplay between awareness and epidemic spreading in multiplex networks[J]. Physical Review Letters, 2013, 111(12): 128701. doi: 10.1103/PhysRevLett.111.128701 [18] GUO Quan-tong, JIANG Xin, LEI Yan-jun, et al. Two-stage effects of awareness cascade on epidemic spreading in multiplex networks[J]. Physical Review E, 2015, 91(1): 012822. doi: 10.1103/PhysRevE.91.012822 [19] KAN Jia-qian, ZHANG Hai-feng. Effects of awareness diffusion and self-initiated awareness behavior on epidemic spreading- an approach based on multiplex networks[J]. Communications in Nonlinear Science and Numerical Simulation, 2017, 44: 193-203. doi: 10.1016/j.cnsns.2016.08.007 [20] PAN Yao-hui, YAN Zhi-jun. The impact of individual heterogeneity on the coupled awareness-epidemic dynamics in multiplex networks[J]. Chaos, 2018, 28: 063123. doi: 10.1063/1.5000280 [21] ERDŐS P, ALFRÉD R. On the evolution of random graphs[J]. Publ Math Inst Hung Acad Sci, 1960, 5(1): 17-60. -
点击查看大图
图(7)
计量
- 文章访问数: 6107
- HTML全文浏览量: 1630
- PDF下载量: 40
- 被引次数: 0
