-
截至2020年2月22日,全国累计报告确诊新型冠状病毒肺炎(COVID-19)病例76 936例,而一项基于7万余例新冠肺炎病例的流行病学调查[1-2]显示,在2020年12月31日前,全国就已有104例患者发病,这表明在各省采取正式防控措施前,COVID-19已在全国各地开始蔓延,因而导致在全国紧锣密鼓地打起“战疫”前,就已经存在诸多的隐形传播者,即尚未被确诊但混入健康人群中不断传播病毒的人,属于非常危险的一类群体。
针对传染病传播的模型主要有SIR、SEIR和SIS模型等,目前已有利用这些模型对新型冠状病毒肺炎传播状况的研究。文献[3]使用基于时变参数的SIR模型对疫情进行评估和预测,得到了预期拐点和最大确诊数,文献[4]基于SEIR模型得到了COVID-19的再生数,文献[5]基于SEIR模型对3种不同潜伏期(5天、7天、10天)下的传播情况进行了拐点预测。除上述文献外,还有其他同样利用这些传播模型的研究[6-7],以及利用元胞自动机[8-10]、一般增长模型[11]和概率分布模型[12-13]对疫情的确诊人数、死亡率等特征进行预测的研究。然而,大部分研究都尚未考虑隐形传播者对疫情的影响,仅仅是将人群划分为易感者(Susceptible, S)、潜伏者(Exposed, E)、感染者(Infected, I)和移出者(Removed, R)4种状态,对潜伏者的划分并不全面,例如是处于医学观察或疑似病例状态的潜伏者还是混入健康人群中的潜伏者(即隐形传播者)。
本文基于SEIR模型,在保留其他3类人群的基础上,将其中的Exposed划分为两部分,即Exposed和Undiscovered,分别表示处于医学观察和疑似状态的人群,以及患病且混入健康人群中未被发现的隐形传播者人群。由于SEIR模型通常要求所考察地区的总人数保持不变,因此疫情分析基于2020年1月25日至2月22日的疫情通报数据[14],该期间由于全国已实施大范围的禁止出境政策,符合模型基本假设。
-
在传统的SEIR模型中,研究对象被分为S、E、I、R 4种类型:
1) S(Susceptible):易感者,表示从未感染病毒的健康人群,他们因为接触了感染者(I)而感染病毒。
2) E(Exposed):潜伏者,表示感染了病毒的易感者在出现症状之前(即潜伏期)所处的状态,这个阶段病毒还未发作,因此暂未传染能力。每位病毒携带者的潜伏期不同,通常假设存在一个平均潜伏期,故每一时刻潜伏者中将会有占p的人群转化为感染者,其中p为平均潜伏期的倒数。
3) I(Infected):感染者,表示病毒发作,开始出现疾病症状的病毒携带者。这类人群具有较强的传播能力,会将病毒传播到接触的易感者。如果假设一名感染者每一时刻平均接触到的人数为λ,则易感者中将会有占λs的人群转化为潜伏者,其中s为易感者所占所有人群的比例。
4) R(Removed):移出者,表示感染者治疗完毕或死亡后的状态。因为大部分传染病患者在痊愈后具有抗体,因此即使与感染者接触也不会被传播,即已退出传播系统。通常假设移出率(一般情况下为治愈率和死亡率的和)为α,则感染者将会有占α的人群转化为移出者。
图1显示了传统SEIR模型的示意图,但其中存在许多可修改的空间,大部分研究是结合实际情况在传统SEIR模型上进行修改,以更贴合现实传播规律。例如,考虑时变传播率[3],引入更多类型的人群[15]等。
在这场COVID-19的疫情防控战中,一般从两个方面来划分不同类型的人群并做出不同措施:1) 监测体温和出行记录判断是否可能携带病毒;2) 被认为可能携带病毒的人群是否确实确诊为感染病毒。如果一个人体温正常且无可疑出行记录,就被定义为“健康的”,不会被采取任何强制措施;相反,如果该人的体温检测和出行轨迹中存在疑点,则会被定义为“可疑人群”,并对该人实施隔离或医学观察等措施。这些“可疑人群”如果被确诊感染了COVID-19,则马上送往隔离病房治疗,而实际未携带病毒的“可疑人群”需要等待一定的观察期后才可解除观察并列入健康人群中。
为此,本文结合上述COVID-19的传播状况,对传统SEIR模型作出如下修改和假设:
1) 对潜伏者的重新定义。本文重新定义潜伏者(E)为上述分析中的“可疑人群”,即被监测出有可疑迹象,实际上可能携带病毒也可能不携带病毒的人群,包括处于医学观察状态的民众和疑似患者这两类。这类“可疑人群”的病毒携带者即使处于医学观察或被隔离,在其他医护人员定期监测其症状的情况下,也依然存在有4~5天的传播窗口期[16]。因此,相对于传统的SEIR模型而言,修改后的模型中,潜伏者中的病毒携带者将会有一定的传播能力,而非携带者经过一定观察期后还会回到易感人群中。
2) 对感染者的重新定义。本文重新定义感染者(I)为“可疑人群”中被确诊感染COVID-19的人群。潜伏者中的病毒携带者在出现症状被送往医院收治后被确诊,确诊后这些潜伏者(E)即刻转变为感染者(I),并被收入严格管控的隔离病房治疗。目前的医疗条件下,确诊患者被隔离后,除进出隔离病房的医务人员外,感染其他人的可能性极小。而医务人员穿戴有密不透风的防护设备,感染可能性也相对较低。因此,相对于原SEIR模型,修改后的SEIR模型中可认为I对S没有传播能力。
3) 引入隐形传播者,即U(Undiscovered)。在COVID-19传播前期,由于COVID-19是新型肺炎,监测措施尚未到位,因此存在许多未监测出来的病毒携带者,这一类人群在本文中被定义为隐形传播者U(Undiscovered)。隐形传播者(U)与潜伏者(E)的最大区别在于,他们被认为是“健康的”而没有被采取任何强制措施,这种情况下他们的传播能力将远远大于潜伏者中的病毒携带者。引入隐形传播者后模型可以更好地刻画病毒的传播情况。
4) 隐形传播者和潜伏者的传播率是恒定的。传统SEIR模型中假设传播率与易感者比例呈正比,即传播者平均接触人数λ×易感者比例s。本文考虑全国范围内的COVID-19传播情况,根据目前已收集到的数据,全国易感者比例始终接近于1(非易感者人数在30万人以内),对传播率的影响较小,因此可认为传播率恒定。
5) 治愈率和死亡率是关于时间的函数。观察疫情数据可知,治愈率和死亡率呈现出明显的时间趋势。现实情况下,随着针对COVID-19治疗技术的研发和改善,治愈率和死亡率必然是会变化的,故本文假设治愈率和死亡率是关于时间的函数。与原SEIR模型中移出率α是恒定的假设相比,本文的移出率是治愈率和死亡率之和,是随时间变化的。
修改后引入隐形传播者的SEIR模型示意图如图2所示。
6) 忽略带病毒潜伏者在医学观察期內始终未有明显症状的情况。目前,大部分携带病毒的医学观察和隔离人群会在14天内发病,出现明显症状而被送往医院,仅极少数带病毒者在14天内始终没有症状。为简化模型,本文不考虑这种发生概率极低的情况。
假定易感者可以被隐形传播者和潜伏者传染,一位潜伏者在单位时间内可将λ1个易感者变为潜伏者(例如潜伏者确诊后寻找与其密切接触的人),而一名隐形传播者在单位时间内传染的易感者为λ2。同时,一些不带病毒的潜伏者在结束医学观察或确认未感染病毒后,将重新变回易感者。医学观察期目前为14天,因此可认为潜伏者中的未携带病毒者每日会有约1/14的数量回到易感人群中。为此假设若携带病毒的潜伏者在所有潜伏者中所占比例为p1,则易感者的变化方程为:
$$ \frac{{{\rm{d}}{S_t}}}{{{\rm{d}}t}} = - {\lambda _1}{E_t} - {\lambda _2}{U_t} + \frac{1}{{14}}(1 - {p_1}){E_t} $$ (1) 隐形传播者在易感人群中传播病毒后,被传播病毒的易感者将变为隐形传播者。这些隐形传播者也有一定概率p2被发现(如在体温或出行轨迹上被监测出疑点,或出现了疑似症状),因而被隔离或送往医院,变为潜伏者:
$$ \frac{{{\rm{d}}{U_t}}}{{{\rm{d}}t}} = {\lambda _2}{U_t} - {p_2}{U_t} $$ (2) 潜伏者可由易感者和隐形传播者转化,既有携带病毒的人群,也有未携带病毒的人群。带病毒人群在一定时间内发作,但由于目前尚未完全确定COVID-19的平均潜伏期,因此假设带病毒潜伏者(在E中所占比例为p1)在单位时间内转化为感染者的概率为p3,同时未带病毒潜伏者(在E中所占比例为1−p1)度过14天观察期后返回到易感者中:
$$ \frac{{{\rm{d}}{E_t}}}{{{\rm{d}}t}} = {p_2}{U_t} + {\lambda _1}{E_t} - {p_1}{p_3}{E_t} - \frac{1}{{14}}(1 - {p_1}){E_t} $$ (3) 潜伏者被确诊后转化为感染者,而感染者则由于治愈或死亡而变为移出者。对于被治愈的移出者,再感染COVID-19的可能性极低,因此已经退出传播系统。假设在t时刻的治愈率和死亡率分别为pC,t和pD,t,则潜伏者和移除者的变化方程分别为:
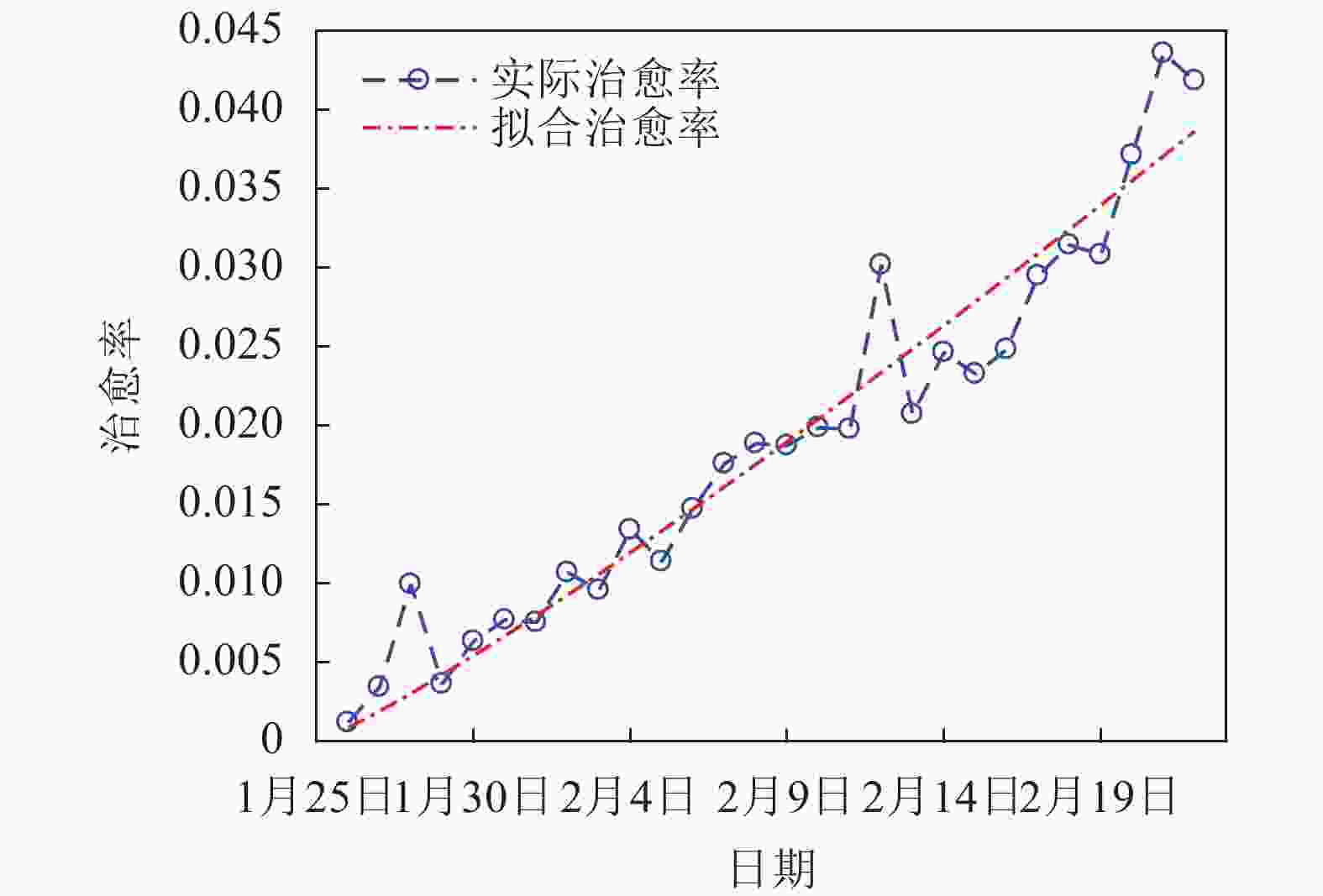
$$ \frac{{{\rm{d}}{I_t}}}{{{\rm{d}}t}} = {p_1}{p_3}{E_t} - ({p_{{\rm{C}},t}} + {p_{{\rm{D}},t}}){I_t} $$ (4) $$ \frac{{{\rm{d}}{R_t}}}{{{\rm{d}}t}} = ({p_{{\rm{C}},t}} + {p_{{\rm{D}},t}}){I_t} $$ (5) 治愈率和死亡率随时间变化的关系可利用疫情数据拟合,pC,t和pD,t分别为当天新增出院人数和新增死亡人数除以上一天感染者的比率,结果分别如图3、图4所示。
pC,t和pD,t随时间推移分别表现出明显的增长和下降趋势,本文使用幂函数对此进行拟合,并去除波动较大值后得到拟合方程如表1所示,拟合效果较好。
表 1 治愈率和死亡率的拟合结果
拟合方程 可决系数R2 调整可决系数 ${p_{\rm{C}}} = 8.683 \times {10^{ - 4}}{t^{1.139\;0}}$ 0.932 3 0.929 7 ${p_{\rm{D} } } = 1.323 \times {10^{ - 2} }{t^{ - 0.572\;4} }$ 0.974 1 0.973 0 注:t=1表示2020年1月26日,对死亡率的拟合去除了2020年2月12日、13日两天的波动较大值。 可收集的数据均以天为单位,因此考虑离散变化的情况,相关微分方程转化为如下的差分方程:
$${S_{t + 1}} - {S_t} = - {\lambda _1}{E_t} - {\lambda _2}{U_t} + \frac{1}{{14}}(1 - {p_1}){E_t}$$ $${U_{t + 1}} - {U_t} = {\lambda _2}{U_t} - {p_2}{U_t}$$ $${E_{t + 1}} - {E_t} = {p_2}{U_t} + {\lambda _1}{E_t} - {p_1}{p_3}{E_t} - \frac{1}{{14}}(1 - {p_1}){E_t}$$ $${I_{t + 1}} - {I_t} = {p_1}{p_3}{E_t} - ({p_{{\rm{C}},t}} + {p_{{\rm{D}},t}}){I_t}$$ $${R_{t + 1}} - {R_t} = ({p_{{\rm{C}},t}} + {p_{{\rm{D}},t}}){I_t}$$ -
由于在2020年2月12日之前,国家卫健委公布的确诊病例中不包含临床诊断病例,因此导致2020年2月12日前后的确诊病例数相差较大,出现明显断层。为此,本文对3个时间段的数据进行拟合:1) 2020年1月25日至2月11日;2) 2020年2月12日至2月22日;3) 2020年1月25日至2月22日。在2020年1月25日至2月22日的拟合中,根据2020年2月12日公布的13 332起临床诊断病例,以非临床诊断病例的增长率为基础,反推出2020年1月25日至2月11日预估的累计确诊病例数、出院数和死亡数。
感染者(I)在本文指的是在第t天的已确诊人群,即“现有确诊数”。但由于2020年2月7日前卫健委公布的数据中未含现有确诊数,因此2020年2月7日前的感染者将用累计确诊数减去累计出院数和累计死亡数之和的结果表示,之后则一直使用官方公布的现有确诊数表示感染者。为便于读者理解拟合时所使用的数据和变量,表2说明了本文对不同时间段拟合时用于表示感染者(I)所使用的变量数据。
表 2 表示感染者所使用的变量
拟合时间段 表示感染者(I)所使用的变量 2020年1月25日至2月11日 2020年1月25日至2月7日:累计确诊数−(累计出院数+累计死亡数) 2020年2月7日至2月11日:现有确诊数 2020年2月12日至2月22日 现有确诊数 2020年1月25日至2月22日 2020年1月25日至2月11日:累计确诊数−累计出院数−累计死亡数(均为调整过的含临床诊断病例的数据) 2020年2月12日至2月22日:现有确诊数 为体现引入隐形传播者后SEIR模型拟合和预测效果的提升,本文还同时用不含隐形传播者的SEIR模型进行拟合,以比较两个模型的拟合和预测效果。基于此,两个模型的拟合目标均为使现有确诊数的均方根误差最小,所求参数分别为(λ1, λ2, p1, p2, p3, U0)和(λ1, p1, p3),其中U0为2020年1月25日当天的隐形传播者数量。
-
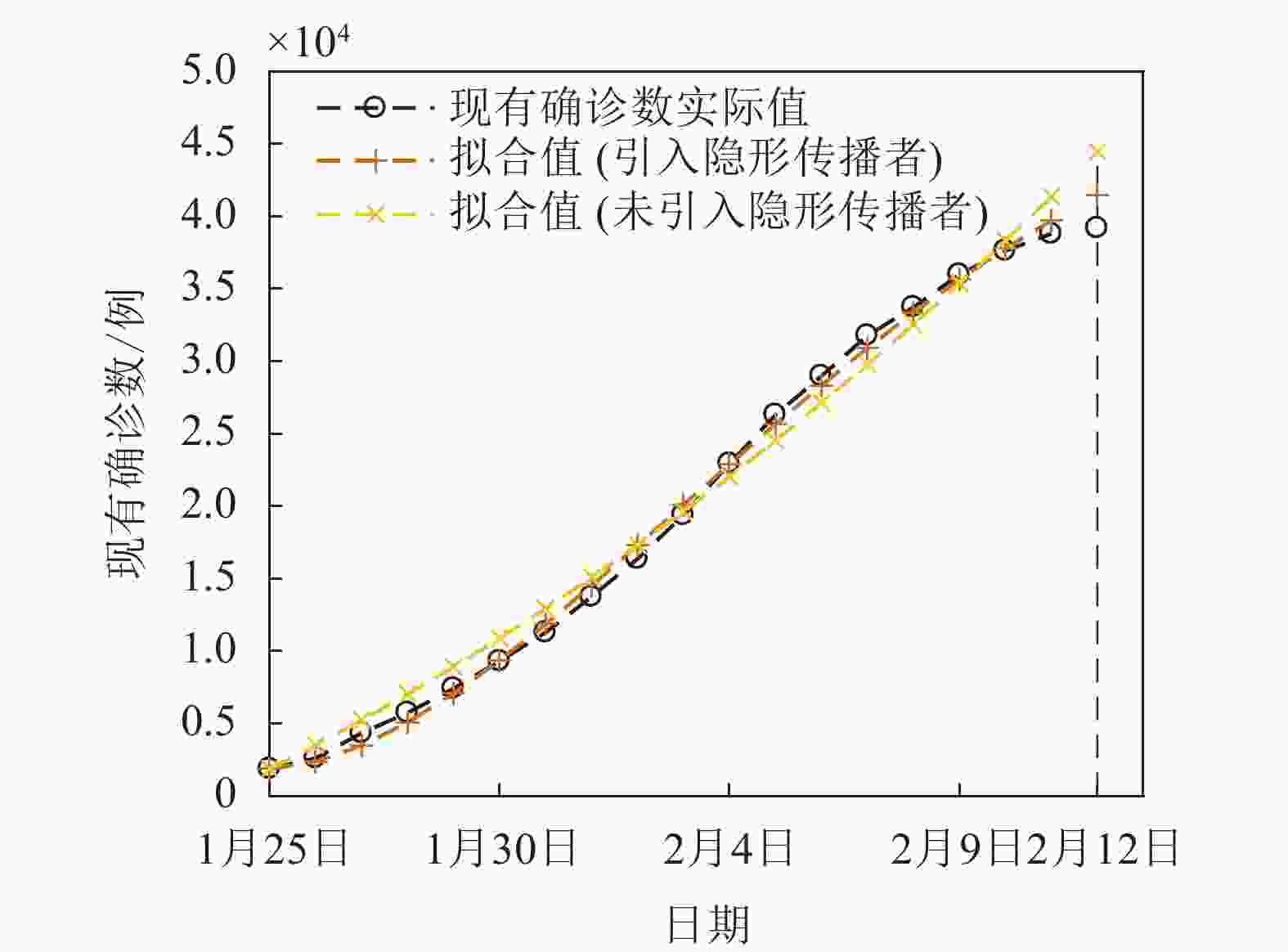
针对2020年1月25日至2月11日的疫情数据,拟合结果如表3、图5所示。由图5可以看出引入隐形传播者后拟合效果有明显提升,对现有确诊人数拟合的相对误差基本控制在0~5%内。以均方根误差(RMSE)和平均相对误差(MAPE)作为评价指标,拟合效果如表4所示,引入隐形传播者的SEIR模型拟合误差比传统SEIR模型降低了50%以上,提升效果明显。以2020年2月12日的非临床诊断病例数据(39 194例)为预测基准,引入和未引入隐形传播者的预测误差分别为5.8%和13.5%,预测精度也有显著改善。
表 3 2020年1月25日至2月11日的拟合结果
隐形传播者的引入 λ1 λ2 p1 p2 p3 U0 引入 0.035 6 0.707 5 0.308 4 0.792 7 0.070 6 37 700 未引入 0.199 6 − 0.473 7 − 0.144 8 − 表 4 2020年1月25日至2月11日的拟合效果评价
隐形传播者的引入 均方根误差(RMSE) 平均相对误差(MAPE)/% 引入 613.20 4.619 9 未引入 1 404.99 10.711 7 观察表3的参数拟合结果,可以看出在疫情爆发前隐形传播者数量已达到约40 000人的水平,因此之后产生了大范围的病毒扩散。此外,潜伏者和隐形传播者的传播率分别为0.035 6和0.707 5,这表明两类不同人群的传播能力确实有显著差别,其中在潜伏者中携带病毒的人群约占30%。这些带病毒人群被确诊的概率为7.06%,换算成潜伏期则约为14天(1/7.06%),等于最长潜伏期,这说明前期诊断技术尚未成熟,存在许多未确诊的带病毒留医人群。如果使用传统SEIR模型,得到的结果为:潜伏者传播率为0.199 6,带病毒人群约占潜伏者的50%,与实际情况有较大偏差,因其将隐形传播者和留医观察人员混为一谈了,这也侧面说明了新的SEIR模型的优越性。
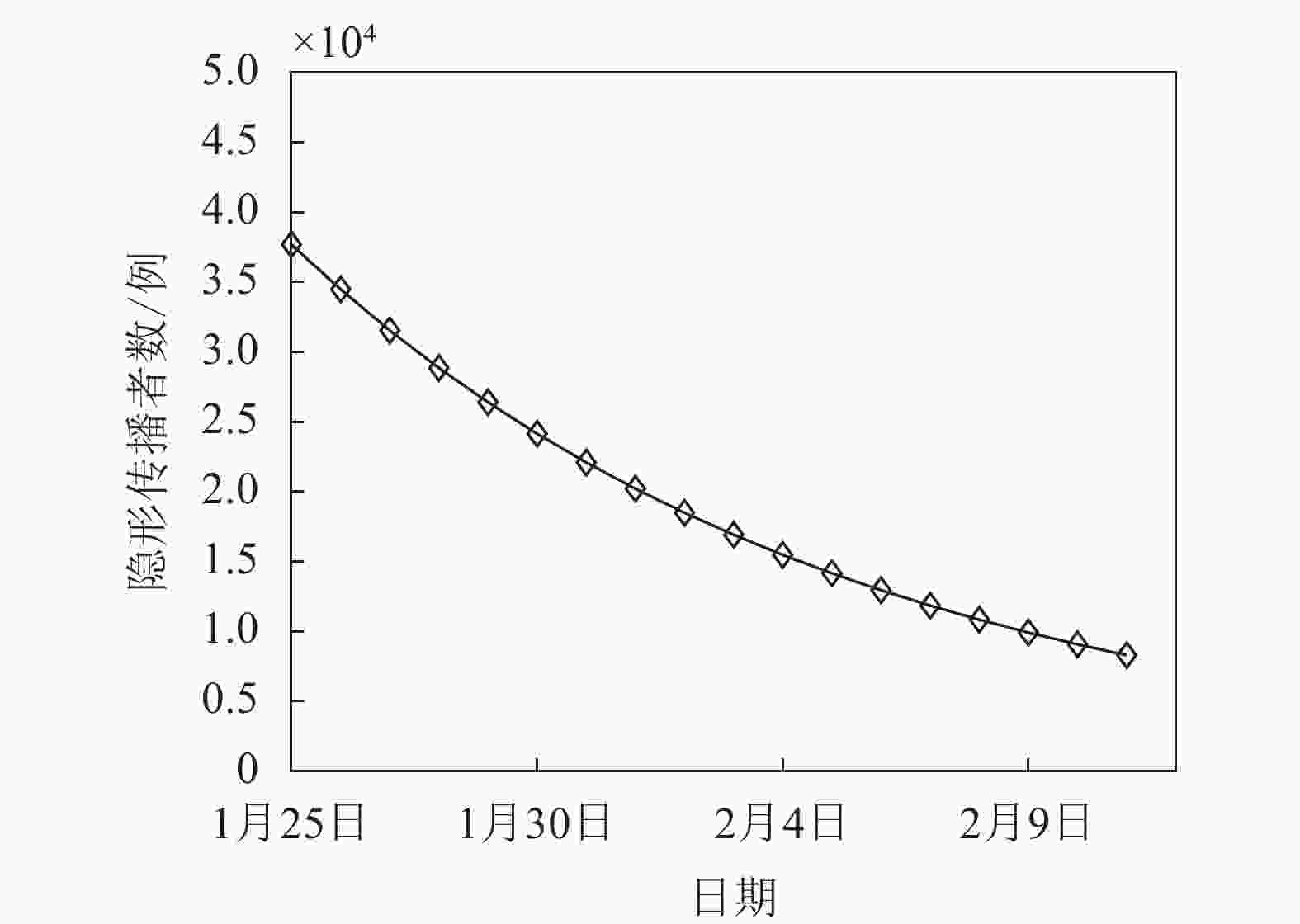
值得欣慰的是,隐形传播者被发现的概率达到80%,这说明检测措施比较到位,隐形传播者的数量变化图(如图6所示)也说明了这一点。随着疫情防控措施推进,隐形传播者数量迅速下降,到2020年2月11日,隐形传播者数已下降至8 000人左右,得到有效控制。
-
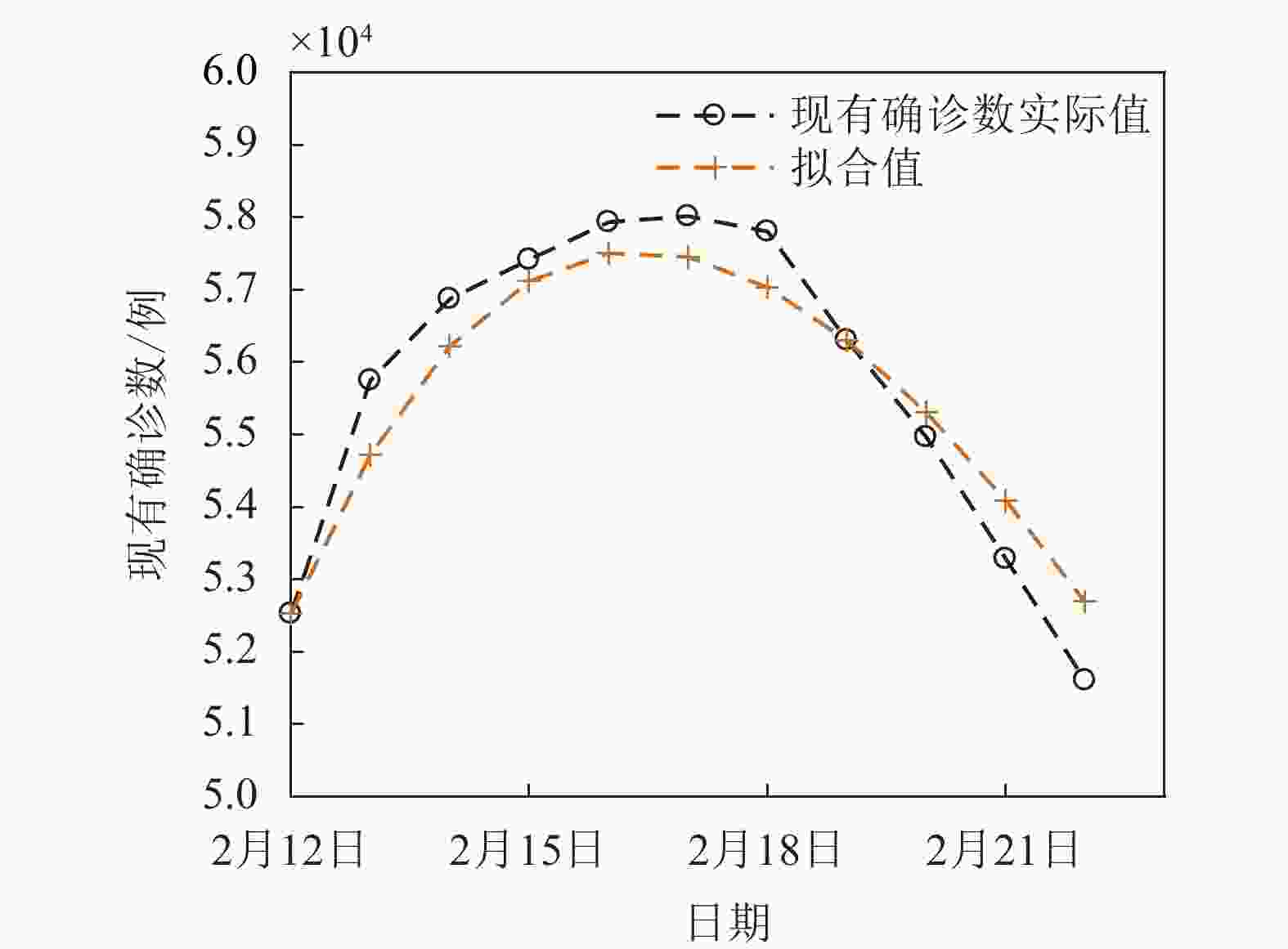
针对2020年2月12日至2月22日的疫情数据,引入隐形传播者的SEIR模型拟合结果显示隐形传播者的传播率已近似于0,且隐形传播者的数量低于100,因而可认为退化为未引入隐形传播者的SEIR模型,最优拟合参数为(λ1, p1, p3)=(0,0.046 6,0.399 9)。拟合结果表明,全国防疫措施已基本做到全方位覆盖,全部隐形传播者几乎都已确诊或留医观察。图7为该阶段的拟合结果图,传统SEIR模型已经较好拟合了该段时间的确诊病例数,均方根误差和平均相对误差分别为678.55和1.08%。
-
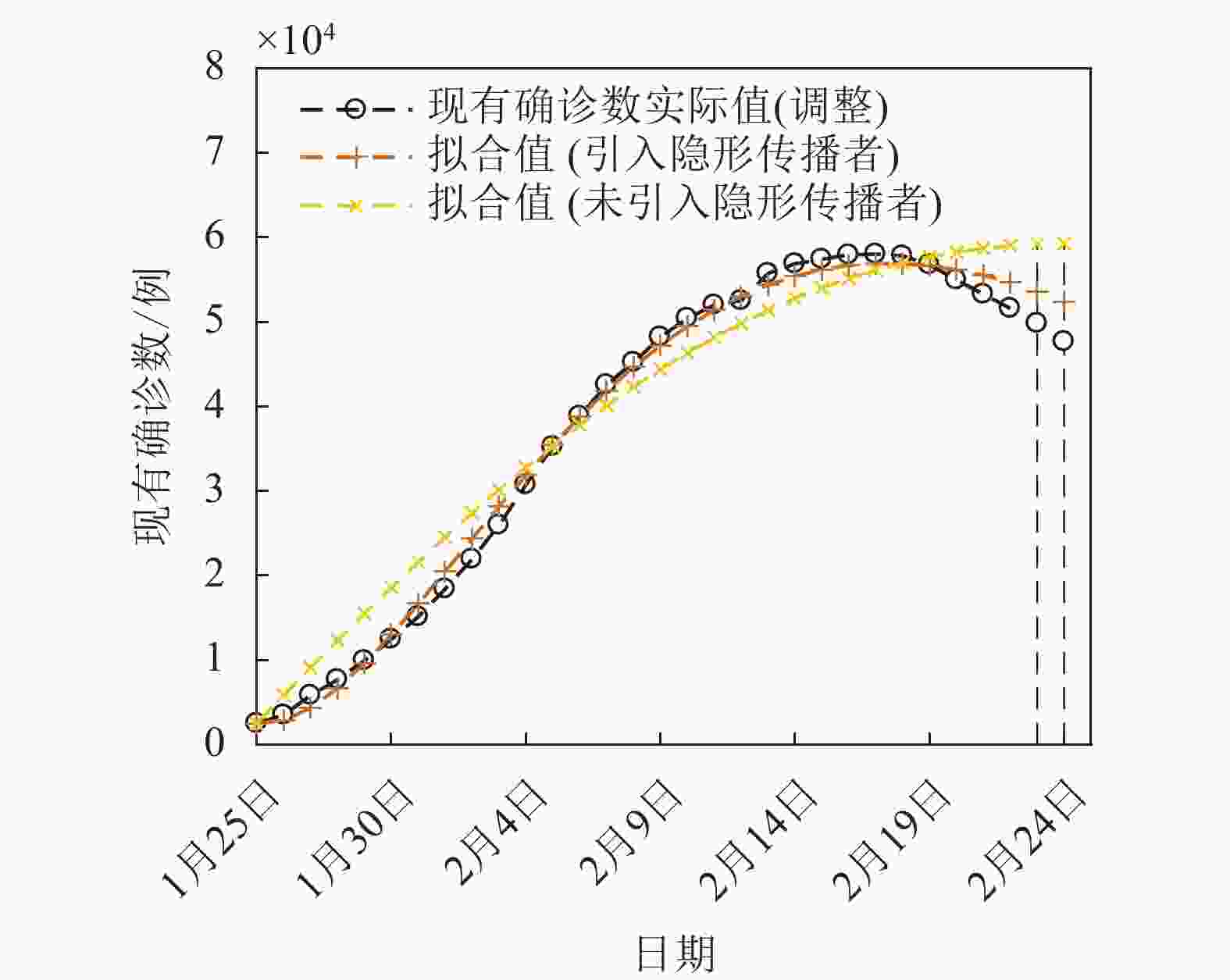
在对完整时间段的疫情数据的拟合中,引入隐形传播者的SEIR模型相较传统SEIR模型的优势更为明显,表5为2020年1月25日至2月22日的拟合结果,由表6可得新的SEIR模型拟合误差在RMSE和MAPE上分别降低了66%和72%以上。利用拟合好的模型预测2020年2月23日至24日两天的现有确诊病例数,其结果如图8所示,图中现有确诊数为调整过含临床诊断病例的确诊数,新的SEIR模型预测误差在理想范围(10%)内。
表 5 2020年1月25日至2月22日的拟合结果
隐形传播者的引入 λ1 λ2 p1 p2 p3 U0 引入 0.027 5 0.875 0 0.129 2 0.986 5 0.130 0 70 013 未引入 0.220 0 − 0.400 5 − 0.356 0 − 表 6 2020年1月25日至2月22日的拟合效果评价
隐形传播者的引入 均方根误差(RMSE) 平均相对误差(MAPE)/% 引入 1 353.85 5.143 7 未引入 4 054.67 18.491 9 表5的拟合结果显示,在将临床诊断病例列入现有病例后,2020年1月25日前的隐形传播者数量实际处于70 000人左右,是非常危险的。在国家严格的防疫措施下,大量隐形传播者被发现并及时隔离治疗,阻止了病毒的大范围传播,p2的大小接近于1也体现了全国监测措施的有效性。图9为模型得到该时间段内隐形传播者的数量变化,截至2020年2月22日,隐形传播者的数量已经控制在2 500名左右。
-
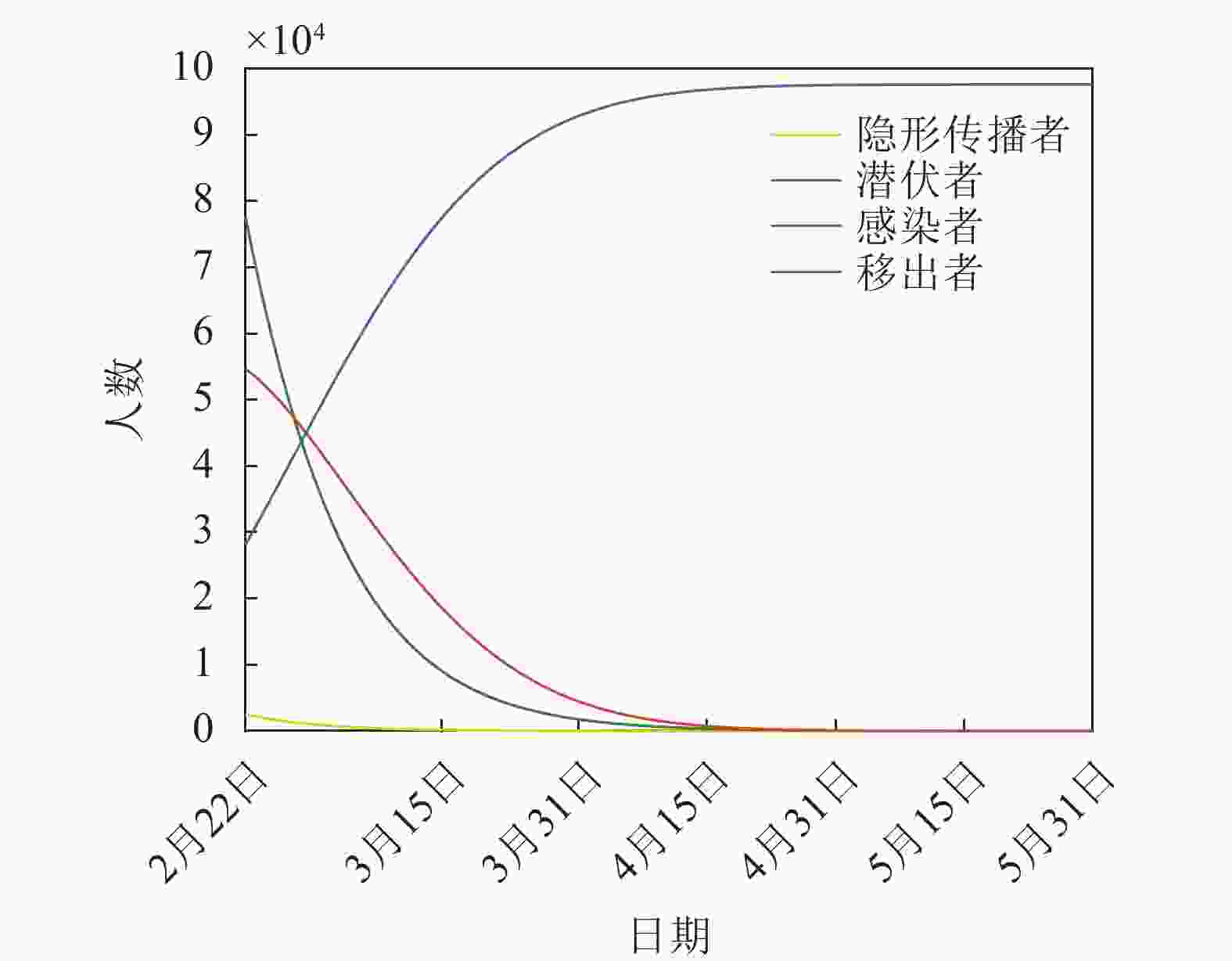
基于拟合好的SEIR模型可以得到未来一段时间的各群体的演化情况,如图10所示。从2020年2月23日至5月31日的仿真结果显示,COVID-19疫情向好发展,在3月中旬,隐形传播者数量已接近于0,潜伏者数量降至1 000以下,感染者数量也将低于20 000。在4月底,所有可能携带病毒的群体数量均接近于0且趋于平稳,因此预测在4月底疫情就能得到完全控制,居民日常生活可完全恢复。最后的移出者数量接近100 000,即预测最终累计确诊数在100 000例左右。
本文认为,真正放心的时刻应为隐形传播者基本被全部确诊或留医观察的时点,这样居民就可以恢复正常的日常生活和工作,也不必再恐慌。基于图10中隐形传播者的演化情况,在2020年3月中旬左右居民可恢复基本的日常出行和工作,是本文认为真正的“拐点”。
-
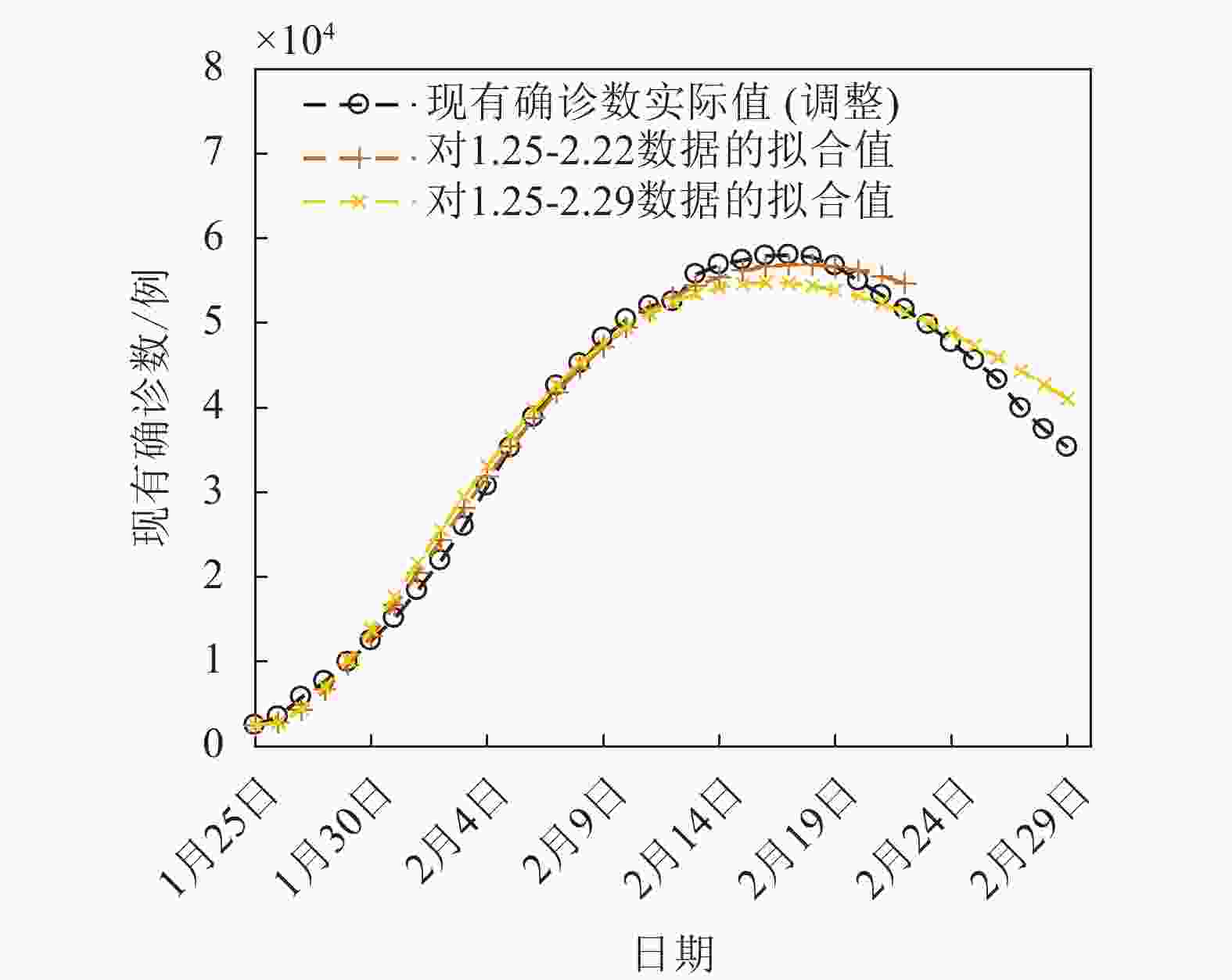
从表4、表6的结果来看,在时间长度增加的情况下,模型的拟合精度会有下降,即模型在拟合传染病早期数据时效果较好,但在拟合后期数据时效果可能会有折扣。为此,本文收集了2020年2月23日至2月29日的疫情数据,并对2020年1月25日至2月29日时间段的疫情进行拟合,拟合后最优参数为(λ1,λ,p1,p2,p3,U0)=(0.015 6, 0.873 9,0.118 0, 0.998 2, 0.140 0, 79 352),RMSE和MAPE分别为2 446.70、6.778 4%。将2020年1月25日至2月22日和2月29日的拟合曲线放在同一坐标轴上,如图11所示,图中,现有确诊数为调整过含临床诊断病例的确诊数。可以看到,补充后期数据后,拟合精度与表6中显示的精度相比确实有一定程度下降,且早期数据的拟合误差也有所增大。
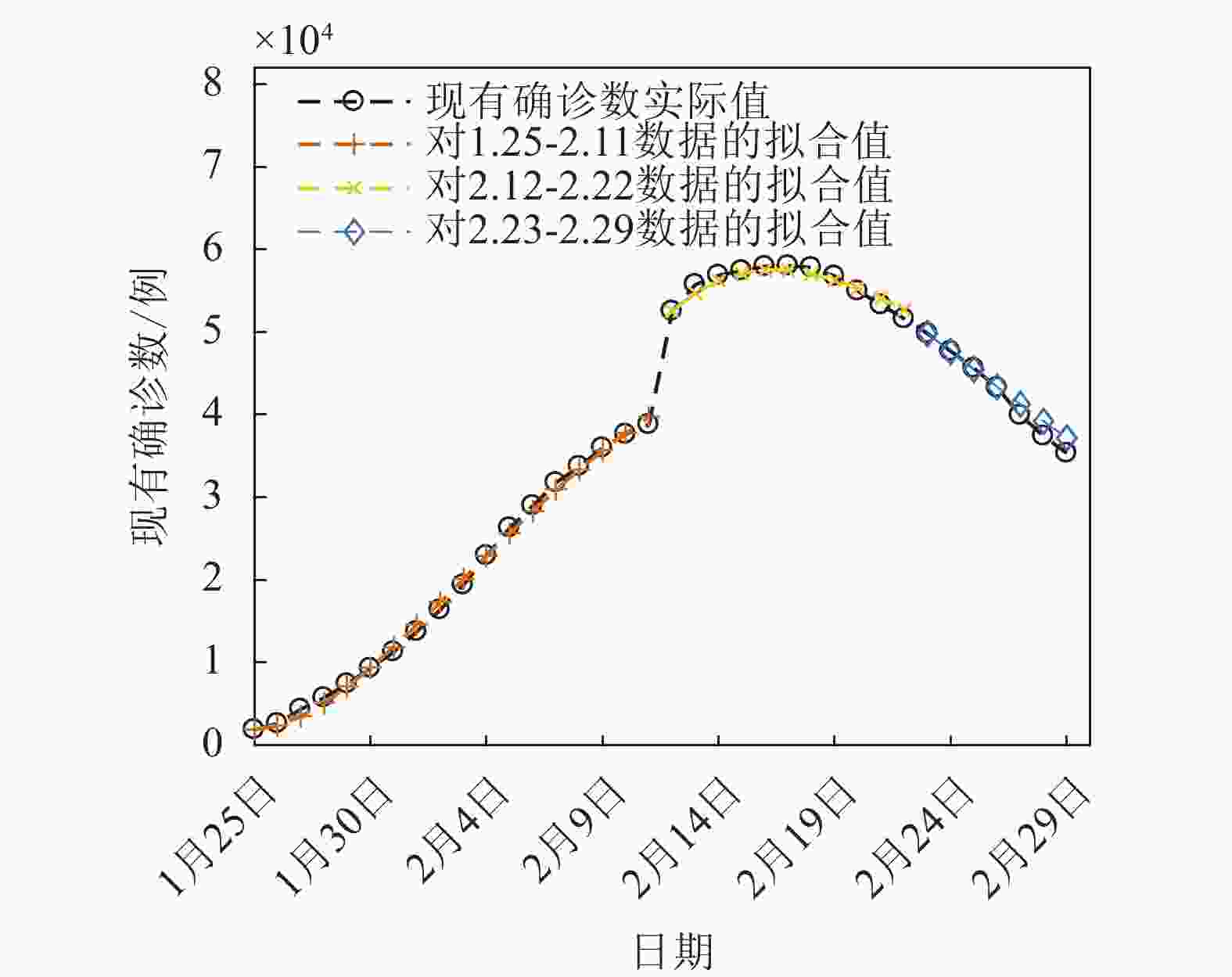
实际上,可以通过分段拟合的方式增加整体的的拟合精度,因为在不同阶段疫情状况和防控力度都有所不同,模型中的参数也应有所变化。图12为分别对2020年1月25日至2月11日、2月12日至2月22日及2月23日至2月29日3个时间段拟合后组合在一起的拟合结果,可以看到整体拟合效果始终较好。此外,还可考虑其他改进措施,例如将模型中的参数设定为时变参数等。
-
本文以传统动力学模型SEIR模型为基础,在原有的易感者、潜伏者、感染者和移出者4个分类上加入隐形传播者,用于表述一类感染病毒但未被发现,而混入健康人群广泛传播病毒的人群。然后,将收集到的COVID-19疫情数据划分为3个时间段:1) 2020年1月25日至2月11日;2) 2020年2月12日至2月22日;3) 2020年1月25日至2月22日。对这3个时间段用引入和未引入隐形传播者的SEIR模型进行拟合,并对拟合结果进行分析。最后,利用对完整时间段拟合的新SEIR模型,演化出未来一段时间内各类人群数量的变化情况,结论如下:
1) 引入隐形传播者的SEIR模型较未引入隐形传播者的模型在拟合和预测性能上均有显著提升。在2020年1月25日至2月11日和1月25日至2月22日这两个时间段内的拟合中,新的SEIR模型的拟合误差在大部分时间点上都在5%以内,相较于传统SEIR模型,在均方根误差和平均相对误差两个评价指标上均降低了50%~70%。同时,引入隐形传播者的模型的预测误差也控制在5%~10%内,属于理想范围。
2) 模型拟合结果显示,在疫情前期,隐形传播者的传染性显著大于普通潜伏者,同时在潜伏者中携带病毒的人群比例约为30%,但这类人群转化为感染者的概率较小,其平均潜伏期约为14天的最大潜伏期,猜测可能是前期诊断技术尚未到位,因此还未能及时对出现疑似症状的人群进行诊断。在后期,由于良好的隔离措施,潜伏者的传染率已变为0,潜伏者中携带病毒人群低于5%,而确诊概率也上升为40%,说明核酸检测技术趋于成熟。
3) 在完整时间段数据的拟合中,初期的隐形传播者数量估计在70 000名左右,而在国家有效严格的防疫措施下,隐形传播者迅速减少,隐形传播者被发现的概率从整体看相当接近于1,在监测传播上做出了巨大成效。截至2020年2月22日,隐形传播者数量已控制在2 500名左右。
4) 2020年2月23日之后的仿真结果显示,疫情整体向好,预计3月中旬隐形传播者基本为0,潜伏者和感染者数量也会大大降低。在4月底,病毒携带者也接近于0,并处于平稳下降趋势,此时居民日常生活可完全恢复。基于演化情况,预测最终累计确诊数为100 000左右,3月中旬为疫情“拐点”。
模型在拟合早期疫情时精度较高,在补充后期数据后拟合精度有一定下降,可通过分段拟合等措施改进模型,增强整体拟合效果。总体而言,引入隐形传播者的SEIR模型相对于传统SEIR模型有明显优越性,可以给COVID-19等类似传染病疫情防控提供较大的参考和指导价值。
Assessment and Prediction of COVID-19 Based on SEIR Model with Undiscovered People
-
摘要: 在传统SEIR模型基础上,引入了“隐形传播者”的概念,并利用2020年1月25日至2月22日的COVID-19疫情数据进行模型拟合,并对结果进行分析。同时,利用拟合好的模型对2020年2月22日之后的演化情况进行仿真。结果显示,引入隐形传播者的SEIR模型在拟合和预测性能上有显著提升,降低了50%~70%的拟合误差;拟合系数表明,在疫情前期和后期携带病毒人群占潜伏者的比例分别为30%和5%,被确诊的概率由7%上升为40%,核酸检测技术趋于成熟;隐形传播者初期人数约为70 000,在国家有效管控下,目前控制在2 500名附近;预测3月中旬为“拐点”,4月底居民可恢复正常生活,最终累计确诊数在100 000左右。Abstract: In this paper the concept of ‘undiscovered people’ is introduced into traditional SEIR model for the research of COVID-19. The model fitting with result analysis is performed by utilizing COVID-19 data from 25 January 2020 to 22 February 2020. And then the fitted model is used to simulate the evolution after February 22, 2020. The results show that the introduction of ‘undiscovered people’ has a significant improvement in fitting and prediction performance, reducing the fitting error by 50% to 70%. The fitting coefficient shows that the virus-laden population accounted for 30% and 5% of exposed people, respectively, in the early and late stages of epidemic. The diagnosed probability of virus-laden population has increased from 7% to 40%, which shows that nucleic acid detection technology is becoming matured. Initial number of undiscovered people is about 70 000, and under effective national control, it is currently controlled at about 2 500. It is predicted that the “inflection point” will be mid-March, then residents can return to normal life at the end of April, and the cumulative diagnosis is about 100 000 finally.
-
Key words:
- COVID-19 /
- dynamic model /
- outbreak assessment /
- SEIR /
- undiscovered people
-
表 1 治愈率和死亡率的拟合结果
拟合方程 可决系数R2 调整可决系数 ${p_{\rm{C}}} = 8.683 \times {10^{ - 4}}{t^{1.139\;0}}$ 0.932 3 0.929 7 ${p_{\rm{D} } } = 1.323 \times {10^{ - 2} }{t^{ - 0.572\;4} }$ 0.974 1 0.973 0 注:t=1表示2020年1月26日,对死亡率的拟合去除了2020年2月12日、13日两天的波动较大值。 表 2 表示感染者所使用的变量
拟合时间段 表示感染者(I)所使用的变量 2020年1月25日至2月11日 2020年1月25日至2月7日:累计确诊数−(累计出院数+累计死亡数) 2020年2月7日至2月11日:现有确诊数 2020年2月12日至2月22日 现有确诊数 2020年1月25日至2月22日 2020年1月25日至2月11日:累计确诊数−累计出院数−累计死亡数(均为调整过的含临床诊断病例的数据) 2020年2月12日至2月22日:现有确诊数 表 3 2020年1月25日至2月11日的拟合结果
隐形传播者的引入 λ1 λ2 p1 p2 p3 U0 引入 0.035 6 0.707 5 0.308 4 0.792 7 0.070 6 37 700 未引入 0.199 6 − 0.473 7 − 0.144 8 − 表 4 2020年1月25日至2月11日的拟合效果评价
隐形传播者的引入 均方根误差(RMSE) 平均相对误差(MAPE)/% 引入 613.20 4.619 9 未引入 1 404.99 10.711 7 表 5 2020年1月25日至2月22日的拟合结果
隐形传播者的引入 λ1 λ2 p1 p2 p3 U0 引入 0.027 5 0.875 0 0.129 2 0.986 5 0.130 0 70 013 未引入 0.220 0 − 0.400 5 − 0.356 0 − 表 6 2020年1月25日至2月22日的拟合效果评价
隐形传播者的引入 均方根误差(RMSE) 平均相对误差(MAPE)/% 引入 1 353.85 5.143 7 未引入 4 054.67 18.491 9 -
[1] 中国疾病预防控制中心新型冠状病毒肺炎应急响应机制流行病学组. 新型冠状病毒肺炎流行病学特征分析[J]. 中华流行病学杂志, 2020, 41(2): 145-151. doi: 10.3760/cma.j.issn.0254-6450.2020.02.003 Epidemiology Working Group for NCIP Epidemic Response, Chinese Center for Disease Control and Prevention. The epidemiological characteristics of an outbreak of 2019 novel coronavirus diseases (COVID-19) in China[J]. Chinese Journal of Epidemiology, 2020, 41(2): 145-151. doi: 10.3760/cma.j.issn.0254-6450.2020.02.003 [2] 中国疾控中心. 1月上旬新冠肺炎已在湖北省外蔓延[EB/OL]. (2020-02-19). http://www.bjnews.com.cn/news/2020/02/19/691757.html. Chinese Center for Disease Control and Prevention. New coronavirus pneumonia has spread outside Hubei Province in early January[EB/OL]. (2020-02-19). http://www.bjnews.com.cn/news/2020/02/19/691757.html. [3] 喻孜, 张贵清, 刘庆珍, 等. 基于时变参数-SIR模型的2019-nCoV疫情评估和预测[J]. 电子科技大学学报, 2020, DOI: 10.12178/1001-0548.2020027. YU Zi, ZHANG Gui-qing, LIU Qing-zhen, et al. The outbreak assessment andprediction of 2019-nCoV based on time-Varying SIR model[J]. Journal of University of Electronic Science and Technology of China, 2020, DOI: 10.12178/1001-0548.2020027. [4] ZHOU T, LIU Q H, YANG Z, et al. Preliminary prediction of the basic reproduction number of 2019-nCoV[EB/OL]. (2020-01-31). https://arxiv.org/abs/2001.10530. [5] 范如国, 王奕博, 罗明, 等. 基于SEIR的新型肺炎传播模型及拐点预测分析[J]. 电子科技大学学报, 2020, DOI: 10.12178/1001-0548.2020029. FAN Ru-guo, WANG Yi-bo, LUO Ming, et al. SEIR-based novel pneumonia transmission model and inflection point prediction analysis[J]. Journal of University of Electronic Science and Technology of China, 2020, DOI: 10.12178/1001-0548.2020029. [6] 吴开琛, 吴开录, 陈文江, 等. SARS传播数学模型与流行趋势预测研究[J]. 中国热带医学, 2003, 3(4): 421-426. doi: 10.3969/j.issn.1009-9727.2003.04.001 WU Kai-chen, WU Kai-lu, CHEN Wen-jiang, et al. Mathematical model and prediction of epidemic trend of SARS[J]. China Tropical Medicine, 2003, 3(4): 421-426. doi: 10.3969/j.issn.1009-9727.2003.04.001 [7] 深圳大学数学与统计学院. 深圳新冠肺炎COVID-19疫情建模与趋势分析[EB/OL]. (2020-02-24). https://mp.weixin.qq.com/s/xIHWJyJxoAiFJMml7mR_dw. College of Mathematics and Statistics, Shenzhen University. Modeling and trend analysis of COVID-19 pneumonia in Shenzhen[EB/OL]. (2020-02-24). https://mp.weixin.qq.com/s/xIHWJyJxoAiFJMml7mR_dw. [8] 吴成来. 基于元胞自动机的传染病传播模型研究[J]. 电脑知识与技术, 2019, 15(9): 185-186. WU Cheng-lai. Epidemic spread model based on cellular automata[J]. Computer Knowledge and Technology, 2019, 15(9): 185-186. [9] 陈长坤, 童蕴贺. 基于元胞自动机的传染病跨区域传播模型研究[J]. 武汉理工大学学报(信息与管理工程版), 2018, 40(4): 359-363, 382. CHEN Chang-kun, TONG Yun-he. Research on inter-regional epidemic model of infectious diseases based on cellular automata[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2018, 40(4): 359-363, 382. [10] 郑三强, 韩晓卓. 多因素制约下的SIR传染病模型的元胞自动机仿真模拟研究[J]. 广东工业大学学报, 2018, 35(5): 51-59. doi: 10.12052/gdutxb.180058 ZHENG San-qiang, HAN Xiao-zhuo. A simulation of cellular automata based on the SIR infectious disease model with multifactorial constraints[J]. Journal of Guangdong University of Technology, 2018, 35(5): 51-59. doi: 10.12052/gdutxb.180058 [11] 张琳. 新冠肺炎疫情传播的一般增长模型拟合与预测[J]. 电子科技大学学报, 2020, DOI: 10.12178/1001-0548.2020037. ZHANG Lin. Fitness of the generalized growth to the 2019 novel coronavirus data[J]. Journal of University of Electronic Science and Technology of China, DOI: 10.12178/1001-0548.2020037. [12] CHEN J H, CHEN S Y, LUH P H, et al. Modeling chronic hepatitis B virus infections with survival probability metrics[J]. Operations Research for Health Care, 2017, 12: 29-42. doi: 10.1016/j.orhc.2017.01.001 [13] MILLER J C. A primer on the use of probability generating functions in infectious disease modeling[J]. Infectious Disease Modelling, 2018, 3: 192-248. doi: 10.1016/j.idm.2018.08.001 [14] 中华人民共和国国家卫生健康委员会. 新型冠状病毒感染的肺炎疫情最新情况[EB/OL]. (2020-01-25). http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml. National Health Commission of the People’s Republic of China. Update on pneumonia outbreak of new coronavirus infection[EB/OL]. (2020-01-25). http://www.nhc.gov.cn/xcs/yqtb/list_gzbd.shtml. [15] 曹盛力, 冯沛华, 时朋朋. 修正SEIR传染病动力学模型应用于湖北省2019冠状病毒病(COVID-19)疫情预测和评估[EB/OL]. (2020-03-03). http://kns.cnki.net/kcms/detail/33.1248.R.20200303.1722.004.html. CAO Sheng-li, FENG Pei-hua, SHI Peng-peng. Study on the epidemic development of corona virus disease-19(COVID-19) in Hubei province by a modified SEIR model[EB/OL]. (2020-03-03). http://kns.cnki.net/kcms/detail/33.1248.R.20200303.1722.004.html. [16] CHEN D B, ZHOU T. Control efficacy on COVID-19[EB/OL]. (2020-02-29). https://arxiv.org/abs/2003.00305. -


 ISSN
ISSN 




 下载:
下载: