-
新型冠状病毒肺炎疫情爆发后[1],国家通过采取最全面、最严格、最彻底的防控举措,目前已经顺利度过流行高峰,新增病例持续下降,国内疫情总体保持在较低水平[2]。下一步的主要任务是有序复工复产复学,同时确保在此过程中不出现疫情反弹的情况,促进经济繁荣、社会稳定。随着疫情的进一步平稳,多个省市已经顺利完成复工复产,复学成为目前广大人民群众最关心的热点问题,也是全国恢复全部正常秩序最需要解决的关键难题。
学校是一个特殊的人群密集场所,学生和老师在教室这个封闭空间中长时间聚集和面对面接触,这种频繁近距离接触增加了相互传染疾病的风险,还有可能成为家庭传播的重要来源[3]。由于现在大中小学都处于封校状态,一旦校园内出现新冠肺炎病例,疫情将会如何进行扩散目前还不得而知。此外,学校出现一定数量病例后为控制疫情,需要及时对新冠肺炎病例进行隔离并采取有效的防控措施。学校停课一般被认为是缓解流行病的最可行策略[4],如针对俄罗斯托姆斯克城市进行的一项研究揭示了短期学校关闭可有效影响人群的行为改变并减少流行病的感染人数[5]。但是学校停课会导致大面积学生隔离,考虑到家长和社会对此问题的关注度,这样做会带来巨大的社会经济成本甚至会导致人群恐慌[6]。所以,在学校出现疫情时,需要选择更加细致科学的防控措施,如可考虑封班级、封年级是否会得到和封校接近的防控效果。
随着新型冠状病毒在全球范围内的爆发,越来越多的研究表明,新冠肺炎患者中存在一定数量的无症状携带者[7],且已有初步证据证明其有传染能力[8]。文献[8]根据官方报道并结合临床资料梳理、分析发现:一位女性在2020年1月10日由武汉回到家乡安阳后,始终无感染新型冠状病毒症状,期间两次胸部CT检查未见异常表现,但新型冠状病毒核酸检测呈阳性,她的父母等5位有接触史的亲属先后被确诊为新型冠状病毒肺炎。这一研究表明:新型冠状病毒的无症状感染者也是可能的传染源,需要重视无症状感染者的隔离及周围人群的防护[9]。
目前对于无症状患者占总病例的比例还有争议。文献[10]对浙江省聚集性病例的研究发现,在391例病人中有54例病人无明显症状,其比例大概为13.8%。文献[11]指出:无症状患者的比例很高,感染者有30%~60%的比例是无症状或者症状轻微。在学校复学后,无症状患者比例的大小如何影响校园环境下的疫情传播也是一个值得关注的重要问题,本文通过射频标签(radio frequency, RFID)采集的师生接触数据仿真和分析校园环境下疫情传播的影响。
除了无症状患者的比例问题外,潜伏期的长短以及潜伏期中新冠肺炎的传染性也是一个值得探讨的问题。利用公开的病例数据,文献[12]分析了468对聚集性病例的序列间隔(serial interval)特征。发现这些传播链中,聚集病例的间隔时间不到一周,大概为4天左右。相比于埃博拉病毒几周以上的序列间隔,新冠肺炎的短序列间隔导致疫情迅速蔓延,很难进行遏制。文献[12]还发现超过10%的患者是由携带病毒但未出现症状的人感染,即所谓的症状前传播。新冠肺炎在潜伏期存在传播且具有隐蔽性[13],给疫情防控带来极大困难。目前仅能确定新冠肺炎在潜伏期内具有传染性,但是准确的传染能力和潜伏期内传染天数还无法确定。
综上所述,鉴于复学后新冠肺炎在校园传播的重要性和严峻性,不仅需要模拟和预测新冠疫情在学校的传播情况,同时也需要研究出有效的防控对策。针对这3个问题,最重要的是通过真实的校园内学生和教师密切接触数据模拟新冠肺炎在校园内的传播:1) 本文模拟了在不同防控措施下的病毒传播,比较封班级、年级和学校等不同措施取得的防控效果;2) 针对无症状患者占总病例的比例还有争议的情况,考虑在无封闭情况和施加防控措施情况,使用仿真手段分析无症状患者比例的大小如何影响校园环境下的疫情传播;3) 针对潜伏期传染性问题,分别对潜伏期内无传染性、潜伏期最后一天具有传染性、潜伏期最后两天具有传染性这3种情况进行了仿真,并比较不同情况的仿真结果。最终,本文分析了无症状患者比例、潜伏期具有传染性这两个重要因素对校园疫情的影响,同时发现了有效的防控对策。在校园中发现病例时,能够及时封闭患者班级、年级就可控制住疫情的发展,并且会取得与封闭学校近似、甚至更好的效果。
-
在早期疾病传播研究中,由于数据采集和存储设备的限制,无法用设备客观记录人与人之间的交互行为,只能通过抽样调查的方式获取人际接触数据。近年来随着物联网和通信技术的飞速发展,获取高分辨率的带有时间标签的人类移动轨迹数据成为可能,从而能够有效感知人际接触。目前比较常用的手段是基于用户手机GPS设备[14]和WiFi热点接入数据[15],也有学者利用大学生一卡通数据进行学生成绩与行为相关性的深入挖掘[16-17]。手机GPS位置数据、WiFi热点接入数据虽然能够满足大规模观测的需求,但是这两种方式定位精度不高,通常只有在用户主动使用手机或者上网时才有记录,因此有可能对用户轨迹的刻画不准确、不连续。为实现更加精确且连续的观测,更好的方式是使用定制的射频标签(RFID)或者手机蓝牙功能对用户间的近距离交互进行连续观测。
本文利用由公开网站提供的使用定制射频标签(RFID)采集的某小学和高中师生密切接触数据[18-19]。小学师生数据是在小学真实环境下使用可穿戴式近距离传感器测量的高分辨率接触数据。学生和老师佩戴RFID传感器,以20 s的时间分辨率检测个体的面对面接触[20]。该数据描述了232名学生和10名老师之间的接触信息,涵盖了为期两天的学校活动。该学校由5个年级组成,每个年级包括两个班级,共10个班级。没有特殊说明,本文的仿真结果都是基于该数据完成的。
-
尽管射频标签数据可以精确记录人与人之间的真实接触,但是对设备的依赖性使实验只能在较小的范围、较短的时间尺度上进行[21-22]。因为原始真实数据仅包含为期两天的接触信息,因此需要对其进行时间维度上的拓展,以保证疫情传播的仿真可以在更长时间段内进行。由于学生每天上课具有很强的规律性和周期性,因此这种数据拓展是合理、有效的,也是一些相关研究的常见做法[19]。在对原数据进行周期性拓展前,需要考虑学生在学校的时间动力学特征。首先,由于真实数据仅描述了学生和教师上学期间(上午8.30到下午5:00)的接触信息,所以假设学生在一天的剩余时间内都与社区保持低强度的接触。此外,中国小学在周六和周日不上学,因此在周末的时间里,学生也被视为不在校,仅与社区有较少的接触。
在每周的时间尺度上,具体的拓展过程如下,根据需要可将两周的数据周期性使用。
1) 奇数周:周一到周五依次对应第一天数据、第二天数据、第一天数据、第二天数据、第一天数据。
2) 偶数周:周一到周五依次对应第二天数据、第一天数据、第二天数据、第一天数据、第二天数据。
3) 周六周日(休息日):这两天学生和老师不在学校,相互之间没有密切接触,他们彼此隔离并与社区有少量接触。
-
复杂网络经典的疾病传播模型包括SI模型、SIR模型、SIS模型、SEIR模型等。SEIR模型在SIR模型基础上考虑了潜伏状态(E),易感状态以单位时间传染概率β转移至潜伏状态,潜伏状态以单位时间传染概率γ转移至感染状态[23]。考虑到新冠肺炎患者具有潜伏期,本文使用具有无症状个体、没有出生、死亡的SEIR模型[24]。在该模型中,个体一共具有5个状态:易感(S)、潜伏(E)、有传染性且有症状(I)、有传染性但无症状(A)、恢复(R)。SEIR传染病模型如图1所示。
1) 当易感个体与传染性个体接触时,易感个体被感染的概率为β,此时被感染的个体由易感态(S)变为了潜伏态(E)。
2) 潜伏个体(E)经过潜伏期(1/μ)之后会具有传染性,变为有症状(I)的概率为1−P(A),变为无症状(A)的概率为P(A)。
3) 有症状个体和无症状个体均在治愈时间(1/γ)之后变为恢复态,处于恢复态的个体具有永久免疫力,不会再被感染。
假设每天结束时都会检测到有症状的个体,并将其隔离,在隔离期间传染性个体将不再传播疾病。需要注意的是,无症状个体无法被检测到,因此无法被隔离。每次模拟都从一个完全易感的人群和一个随机选择的传染个体开始,该传染性个体被选为有症状(I)的概率为1−P(A),无症状(A)的概率为P(A)。本文为SEIR模型考虑以下参数值。
1) 潜伏期(1/μ):4天。文献[25]指出新冠肺炎的潜伏期中位数为4天。
2) 恢复期(1/γ):10天。文献[26]指出治愈患者平均住院时间为10天左右。
3) 感染率(β):7.0×10−4 s−1。虽然感染率可以通过R0除以传染期天数进行计算,但在实际传播过程中,人与人只要面对面交流就有可能被传染,参照以前针对真实数据的研究设置[19],本文假设每24 min接触就会导致一个人被感染。
4) 社区感染率(βcom):7.0×10−8 s−1。如上所述,数据仅仅描述了校园内个体之间的接触,然而在校园外的易感个体也有接触传染性个体的情况,因此认为易感个体在校外也有被传染的可能性。为简单起见,假定这种可能性是统一的,并且通过固定的感染率将其引入模型,即易感个体在校园外被感染的概率为βcom。由于学生在校园外仍然存在很强的社区隔离,所以将社区感染率设为一个很低的值。
5) 无症状概率:定义为0.3。目前各国新冠肺炎无症状患者占总病例的显著比例不同,无症状概率从0.1~0.6都有可能,因此将无症状概率定义为0.3,并且分别讨论了无症状概率为0.1、0.3、0.5、0.6这4种情况。
在仿真过程中,以时间步长dt执行仿真,该时间步长由真实接触数据集的时间分辨率确定,即20 s。此外,对于每个被感染的个体,从1/μ和1/γ的正态分布以及等于其十分之一的标准偏差中随机抽取被感染个体的潜伏期和传染期的持续时间。
-
文献[27]提出有效距离(effective distance)的概念,在H1N1和SARS传播的真实数据上验证了该度量方法的有效性,成功预测了疾病的传染规律。该测度说明:根据地理距离以及传统的欧式距离等方法不适用于度量真实个体间的距离,而疾病传播与个体间的有效距离密切相关。
在本文中,通过学生之间的接触次数(时间)计算有效距离。在计算之前,需要计算两个学生之间的接触概率Pmn。首先计算接触数据Imn,它表示m和n之间的接触次数。Gm表示当前学生m与其他学生接触次数的总和,因此m和n接触概率Pmn为:
$${P_{mn}} = \frac{{{I_{mn}}}}{{{G_m}}}$$ (1) 因为对数具有可加性,所以对得到的接触概率Pmn取对数,最终求出有效距离dmn为:
$${d_{mn}} = 1 - \log{P_{mn}}$$ (2) 式中,m、n为任意两名学生;dmn是两者之间的有效距离。
将学生之间的有效距离存放在矩阵D中,Dmn表示学生m与n之间的有效距离(dmn),通过对该矩阵的可视化能够得到图2所示的结果。图中x轴与y轴分别对应232个学生,除五年级以外,每隔47个学生代表一个年级,五年级为最后的44个学生。对于每个年级,前23个学生代表第一个班级,剩下的学生代表第二个班级。将学生之间的有效距离通过颜色表示,有效距离与颜色的映射关系如图中右侧颜色板所示。
从图2中可以发现:同一班级的学生之间有效距离最短,说明学生间的接触主要都是在一个班级中。对于一年级和三年级的学生,由于他们与同一年级的其他班级学生也有明显的接触,所以在这两个年级内,不同班级之间的有效距离也比较短,而其他年级中不同班级间学生的有效距离较大。总体来看,不同年级的学生之间有效距离都较大,说明不同年级之间的相互接触较少。
-
两个学生之间有效距离越短,说明他们之间的接触越多,新冠肺炎在他们之间越容易传播。针对图2的结果,能够得出如下结论:在同一班级内病毒最容易传播,在有些年级中不同班级之间也较易传播,但是在不同年级之间传播病毒的可能性较小。针对学生之间的有效距离,可以制定以下防控措施:
1) 班级封闭:当班级中有症状个体数量到达固定阈值时,将班级封闭一段时间。
2) 年级封闭:当年级中有症状个体数量到达固定阈值时,将该年级封闭一段时间。
3) 学校封闭:当学校中有症状个体数量到达固定阈值时,将全校封闭一段时间。
以上描述的所有防控措施均取决于两个参数:封闭触发阈值(检测到的有症状个体的数量)以及封闭时间。本文研究考虑封闭触发阈值为1,封闭时间为14天。例如:阈值为1、封闭时间为14天的封闭班级措施,表示当任意一个班级的有症状个体数大于1时,将该班级的学生隔离14天。
对应所有的防控措施,被封闭的师生被认为在封闭期间无任何接触,但是与社区还有少量接触。封闭结束后,该班级(年级、学校)重新开放,相应的学生回到学校,在校园中重新具有被感染的可能性。被封闭的班级(年级、学校)在开放之后如果达到封闭条件,也会被再次封闭。
-
针对上述提出的几种防控措施,本文分别进行了2 000次模拟以保证结果的可靠性。
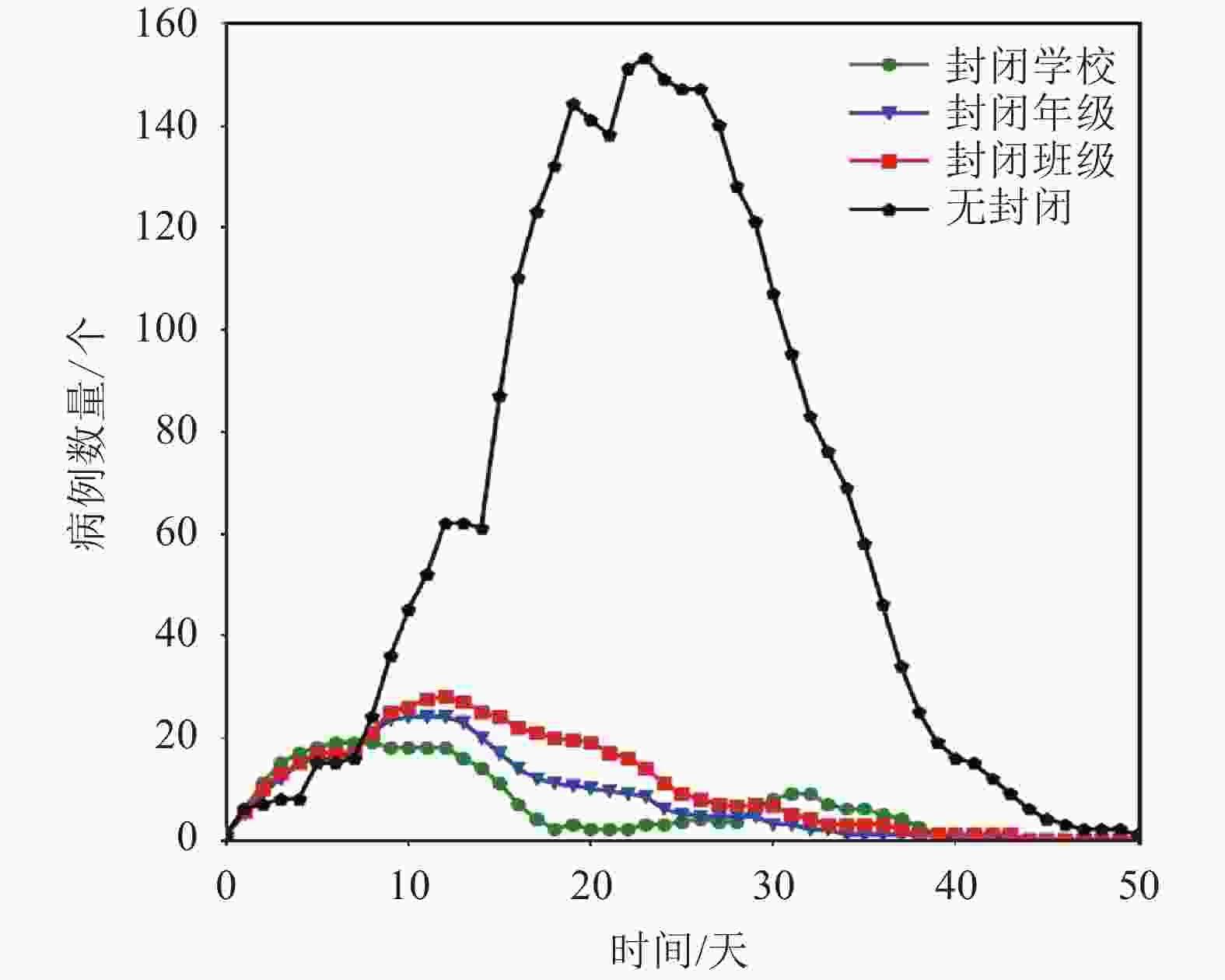
为了比较每种封闭方式的防控效果,本文进行了如下分析。图3为仅考虑导致罹患率(受疾病影响的个体比例)高于10%几种防控措施的感染个体中位数随时间变化情况,第0天代表第一周的星期一。从图中可发现在无封闭情况下,0日到20日之间感染速率要明显大于恢复速率,病例数量开始迅速增加。由于在25日时几乎不存在易感个体,所以从25日之后病例数量开始下降,直到50日时疫情才彻底结束。施加防控措施以后,每一种封闭方式均会降低感染个体的规模,感染个体的峰值均不会超过30个,并且从第12日开始,疫情出现好转,病例数量开始下降。
封闭学校后,在20日之前的防控效果要优于封闭年级和封闭班级,其峰值仅会到达20个。但从曲线上可以看出,在封闭学校情况下,从20日开始病例数量开始增加,在29日之后封闭学校导致的病例数量甚至要高于封闭班级和封闭年级。通过对模拟过程的分析,找到了出现这种情况的原因。由于封闭学校会造成大面积学生被隔离,这些学生被隔离后将会与社区接触。即使在社区感染率非常低的情况下,也依旧存在被感染的可能,一旦有学生被感染,并在返校时没有出现症状,将会导致病毒的再次传播。而对于封闭班级和封闭年级,由于被隔离的学生数量较少,所以社区感染风险也随之降低,在隔离期间社区感染不会造成太大的影响。
综上所述,当在学校发现一个病例时,就要立即对该学校、年级或班级进行封闭,隔离以后都会有非常好的防控效果。同时要做好隔离后的保护工作,避免学生在隔离期间被感染。研究发现,封闭学校会导致最大数量的学生离开校园环境,如果他们回家后的隔离措施不够完善,反而会导致比封闭班级和封闭年级更差的效果。
-
在上面章节中,仿真实现了小学环境下疫情的可能传播和不同封闭措施对疫情的影响。由于上述数据是基于国外的小学获取的,和国内小学环境有一些明显区别。如数据中每个班级只有20名左右的学生,而国内小学一般人数都在40人以上。此外,小学环境和初中、高中的学生环境也有差异。为了验证本文所进行的传播仿真和具体措施是否具有通用性、鲁棒性,本文也获取了与上述研究数据不同的中学学生真实接触数据[28]。该数据描述了329名学生之间的接触信息,涵盖了为期5天的学校活动,一共有4个年级,每个年级中班级数量不等,共9个班级,且每个班级大约有40名学生。
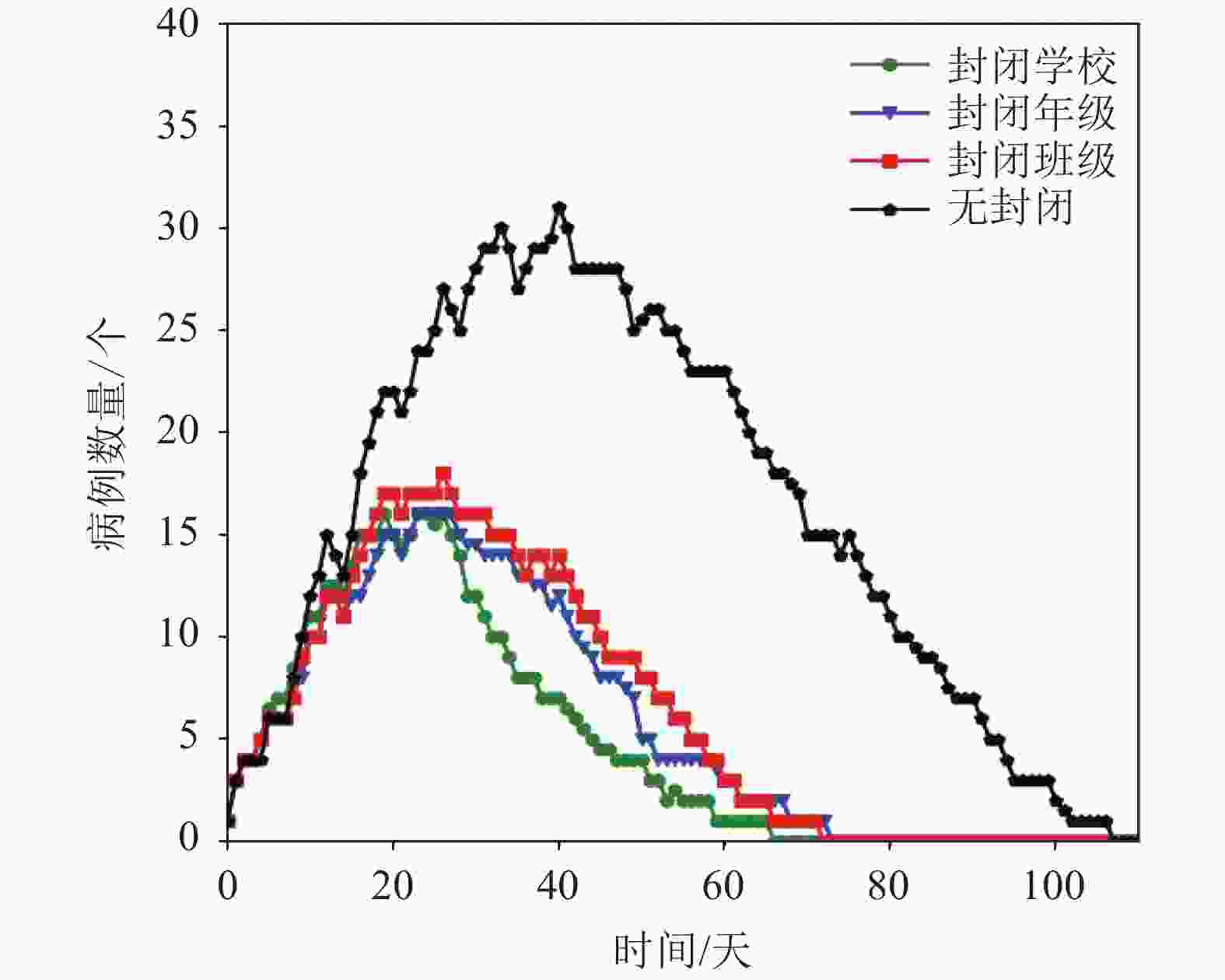
针对中学学生实际接触数据,本文再次研究了在不同校园环境下施加防控措施是否会取得控制疫情的效果。图4显示了基于该数据,在考虑导致罹患率高于10%时,几种防控措施的感染个体中位数随时间变化情况,第0天代表第一周的星期一。从图中可以看出,结果基本上和小学环境类似。与无封闭下的疫情情况相比,每一种封闭方式均会降低感染个体的规模,感染个体的峰值均不会超过20个,病例数量均会从25日开始下降,而且班级和年级封闭几乎取得了和学校封闭相同的效果。
同时也发现中学环境下的疫情情况与上述小学的疫情情况存在一些不同之处。首先,在无封闭情况下,病例的峰值仅仅达到30个,并且在到达峰值之后,不会出现病例数量大幅度增加的情况。其次,在施加封闭学校措施后,病例数量不会出现二次上升,从25日开始到疫情结束,病例数量始终处于下降趋势。最后,通过对小学数据的仿真能够得出封闭年级和封闭班级会与封闭学校产生近似的效果,而这种近似效果在该高中环境下体现的更为明显。
通过对该高中学生实际位置数据的分析,本文发现参与实验的高中学生虽然都在一个学校,但学生的班级位于高中教学楼的不同位置。这导致学生除了与本班级同学接触以外,与其他班级的学生几乎没有接触。这种教学和管理方式,使病毒很难在该学校传播。通过对该高中的疫情分析,得到如果能够在复学期间将各个班级或各个年级之间实施较好的物理隔离,并且减少同一班级学生之间的接触次数,在这种环境下病毒的传播速度会明显下降,产生的病例规模也会降低,即使不封闭学校,也会取得很好的防控效果。
-
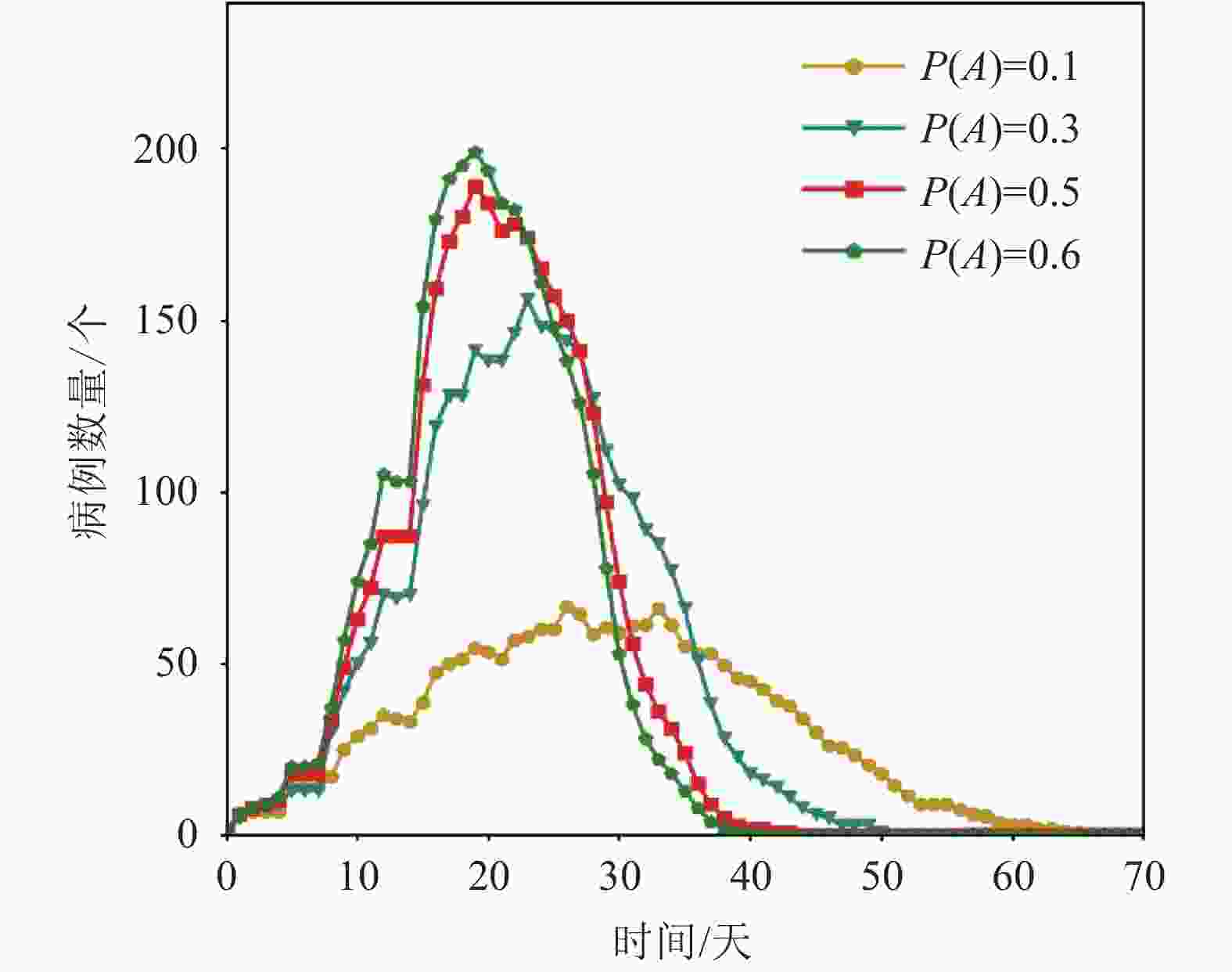
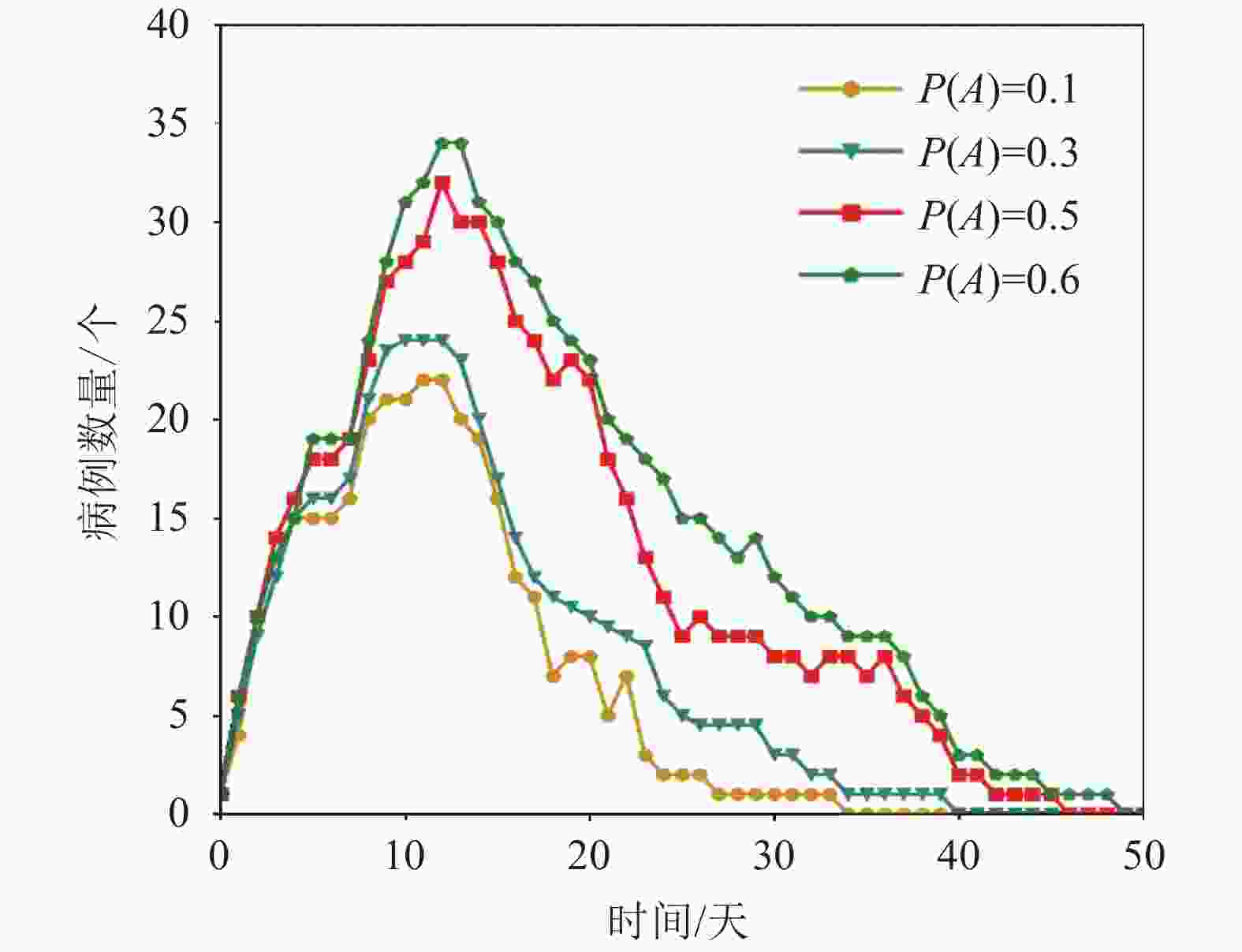
在学校复学后,无症状患者比例的大小如何影响校园环境下的疫情传播是值得关注的一个重要问题。由于目前无症状患者的比例还无法确定,本文设定了不同的无症状概率并分别进行仿真。图5和图6分别描述了在不同无症状概率P(A)下,2 000次模拟中病例个体中位数随时间的变化情况(仅考虑罹患率大于10%的模拟)。
图5表示在无防控措施下的疫情情况,可发现不同的P(A)值所对应的疫情情况有明显差别。随着P(A)的增大,病例增加的速度也越快。当P(A)=0.1时,病例数量的峰值最多会达到60个,并在35日之后病例数量开始下降。当P(A)≥0.3时,感染速度和感染规模出现了明显提高,在2 000次模拟中会有90%以上的模拟导致疫情爆发,累计病例的平均数量均大于200个。P(A)仅为0.3就会导致病例数量的峰值大于100个,而当P(A)=0.6或0.5时,由于无症状患者数量增加,每天结束时并不能检测到这些患者,所以他们依旧在传播病毒,这导致了病毒传播速度非常快,在20日之前就会将病毒传染给所有师生。
图6表示了在施加防控措施下的新冠疫情情况。定义防控措施为年级封闭(阈值为1,封闭14天),并在不同无症状概率下进行了模拟。可发现当施加防控措施以后,疫情的爆发得到了一定控制,并且病例数量均会从12日开始下降。即使P(A)=0.6或0.5,病例数量的峰值也不会超过35个。与无防控措施相比,病例数量得到了很大程度下降。当P(A)≤0.3时,病例数量的峰值已经不会超过25个,P(A)=0.3和P(A)=0.1会出现相似的变化曲线。
-
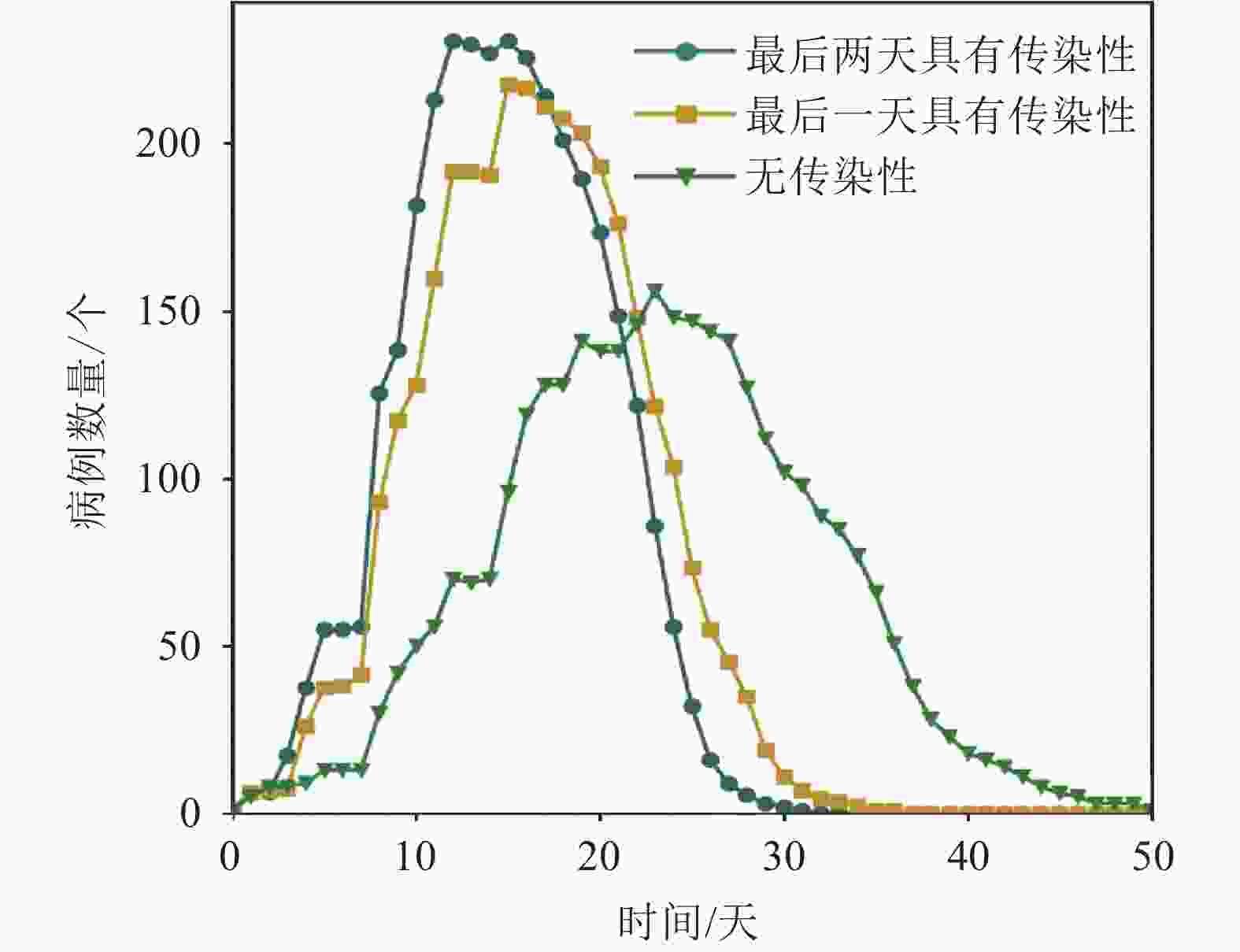
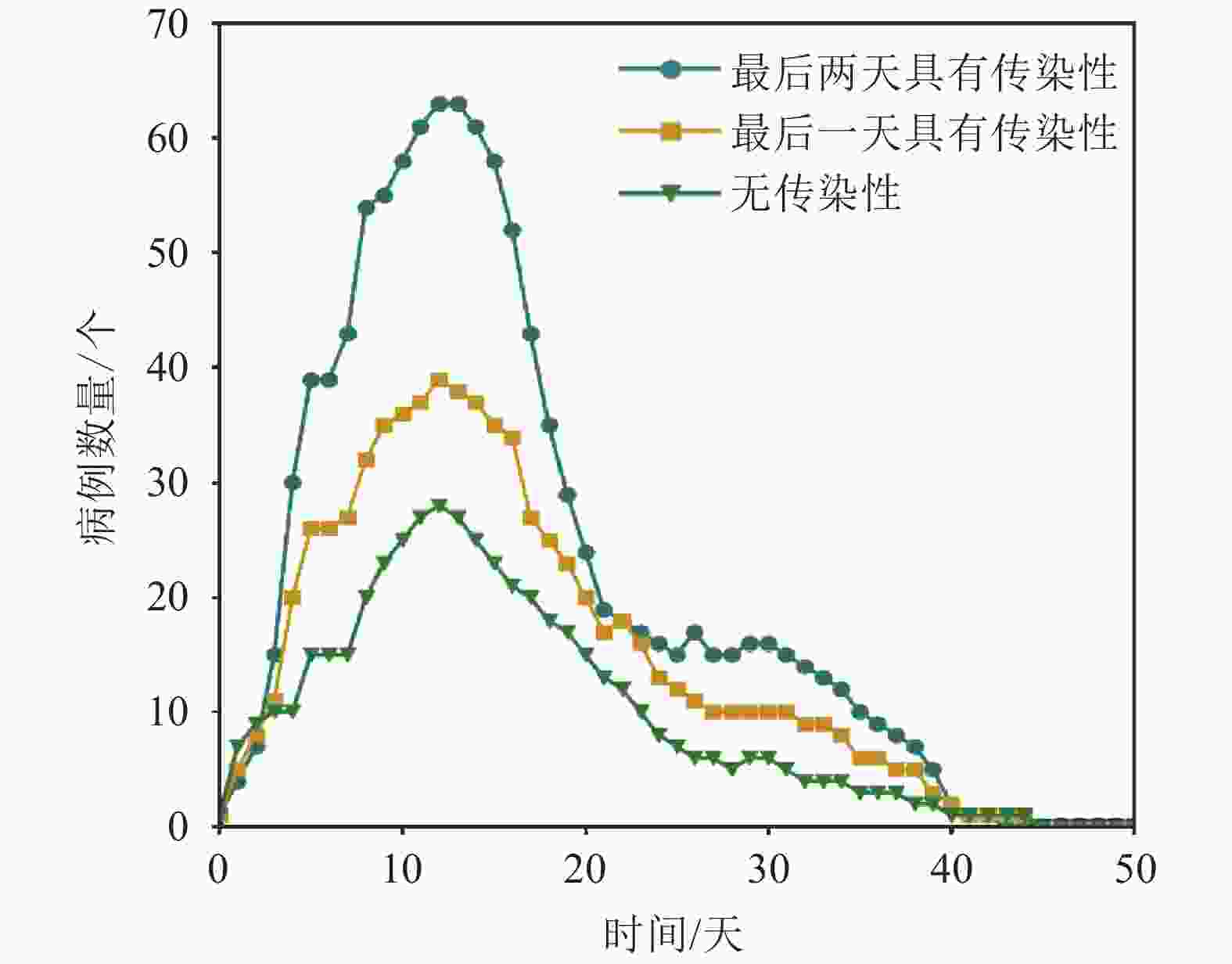
新冠肺炎在潜伏期内会传播且具有隐蔽性[13],这种现象为疫情防控带来极大的困难。目前仅能确定新冠肺炎在潜伏期内具有传染性,但是准确的传染能力和潜伏期内传染天数还无法确定。为了比较潜伏期传染性对疫情传播的影响,本文分别对潜伏期内无传染性、潜伏期最后一天具有传染性、潜伏期最后两天具有传染性这3种情况进行了模拟。图7和图8描述了在这3种情况下,2 000次模拟中病例个体中位数随时间的变化情况(仅考虑罹患率大于10%的模拟),分别表示了在无防控措施下疫情情况和在施加防控措施(阈值为1,封闭14天的年级封闭措施)下的疫情情况。
从图7中可以看出,相比于其他两种情况,当潜伏期内无传染性时疫情的传播速度最慢,病例数的峰值也最低。当潜伏期内具有传染性时,无论传染天数为多少,在20日前病例数都会到达峰值,并且传播速度会随着传染天数的增加而加快。值得注意的是,在这3种情况下2 000次模拟中罹患率大于10%的百分比均大于90%,并且在仅考虑罹患率大于10%的模拟时,累计病例的平均数量均接近242个(全部师生)。也就是说,无论潜伏期内传染性是何种情况,如果不施加防控措施,均有很大概率造成疫情爆发。
在施加防控措施的情况下,本文对这3种情况再次进行模拟。从图8中可以看出,病毒的传播速度依旧会随着潜伏期传染天数的增加而加快,病例数量的峰值也会随着传染天数的增加而增大。但对于每一种情况,与无封闭措施相比,施加防控措施均会导致病例规模降低。对于潜伏期最后一天有传染能力的情况,在无封闭时会造成与潜伏期最后两天有传染能力近似的效果。但当施加防控措施以后,两者出现很大的差别,潜伏期最后一天有传染能力时,病例数量的峰值要小于40个;而当潜伏期最后两天有传染能力时,病例数量的峰值已达到60个以上。值得注意的是,无论是哪种情况,在12日疫情都会出现转折和下降。从这日开始一直到疫情结束,病例数量会明显下降,并且不会再有爆发的可能。
-
本文基于真实高精度的人际接触数据,仿真和分析了复学背景下新冠肺炎在校园内的传播情况。同时模拟了在不同防控措施下的校园疫情,并分析了无症状概率和潜伏期传染性对疫情的影响,提出了有效的防控策略。
首先,基于学生之间的有效距离发现:在校期间,学生几乎只与本班级或本年级的同学接触,病毒在同一班级或同一年级内更容易传播。其次,基于仿真结果发现在无防控措施情况下,病毒将会在校园迅速扩散,并有很大的几率造成全部感染。施加防控措施之后,病毒传播速度明显下降,累计感染人数也明显减少。从疫情的整个周期来看,封闭年级会与封闭学校取得近似的效果,都会抑制疫情的爆发。虽然在初期封闭学校会取得很好的防控效果,但大面积的学生隔离不仅会增加社会经济的负担,也会增加学生在社区被感染的几率,从而导致病毒的再次传播。因此为了控制疫情的发展,当在年级发现一个病例时,就要及时的对该年级进行封闭,并且在隔离期间做好防护工作,同时严格避免学生在社区被感染。
无症状概率和潜伏期内传染性对于新冠肺炎在校园内传播的影响,本文发现在没有防控措施的情况下,随着无症状概率的增加,病毒的传播速度也会加快,产生的病例规模也会增大。在施加防控措施的情况下,无论无症状概率等于多少,疫情的爆发都会得到一定控制,并且病例数量均会在较短时间内开始下降。在无封闭情况下,即使潜伏期内无传染性,也会造成全部的学生和老师被感染。而在有封闭情况下,即使潜伏期最后两天有传染能力,也能做到疫情的控制,并且疫情会迅速出现好转,病例数量会明显下降,并且不会再有爆发的可能。
综上所述,当学生和老师回到学校以后,不仅要防止传染源出现,也要在疫情出现时做好防控措施的准备。一旦病毒在校园内开始传播,首先要关注同一班级、年级的学生,并及时对该班级、年级进行隔离。如果能够在复学期间将各个班级或各个年级之间实施较好的物理隔离,并且减少同一班级学生之间的接触次数,在这种环境下病毒的传播速度会明显下降,产生的病例规模也会降低,即使不封闭学校,也会取得很好的防控效果。最后,也要关注无症状患者和在潜伏期内具有传染性的患者,在取消隔离开始复学时,需要对每一位学生进行关注和检查,避免无症状传染者进入学校。
Infection and Prevention of COVID-19 in Schools Based on Real-Life Interpersonal Contact Data
-
摘要: 随着新冠肺炎疫情在中国的稳定,复学成为目前广大人民群众最关心的热点问题。学生和老师在学校长时间聚集和面对面接触增加了相互传染疾病的风险,虽然学校停课一般被认为是缓解流行病的最可行策略,然而大面积的隔离往往伴随着高昂的社会经济成本甚至会造成社会恐慌。所以在学校出现疫情时,需要尝试使用更加细致科学的防控措施。该文基于真实人际接触数据模拟新冠病毒在校园内的传播,通过计算学生之间的有效距离制定防控措施。研究发现学生在校园内与同班级、同年级学生接触较多,所以当在校园中发现病例时,及时封闭患者班级、年级就可控制住疫情的发展,能取得与封闭学校近似、甚至更好的效果。此外,在无封闭和施加防控措施情况下,分别对无症状患者比例和潜伏期传染性对校园疫情影响进行了分析。在施加防控措施后,每种情况下的疫情都会得到控制,并且会很快迎来疫情好转的时间点。该研究有助于学校选取合适的防控措施,准确评估无症状患者和潜伏期传染性对疫情的影响。Abstract: With the stabilization of the COVID-19 in China, the resumption of study has become the hottest issue most concerned by the people. The long-time gathering and face-to-face contact of students and teachers in schools increase the risk of their mutual infection. Although school suspension is generally considered to be the most feasible strategy to alleviate epidemics, large-scale isolation is often accompanied by high socio-economic costs and even social panic. Therefore, when an outbreak occurs in schools, we need to try to use more detailed scientific prevention and control measures. In this study, the spread of the COVID-19 in schools is simulated based on real interpersonal contact data, and the prevention and control measures are formulated by calculating the effective distance among students. This study finds that students have more contact with students in the same class and grade in schools. Therefore, when cases are found in schools, the development of the epidemic can be controlled by closing the patient's class and grade in time, and it will achieve similar or even better results than the closed school. In addition, in the absence of closure and the application of prevention and control measures, the impact of the proportion of asymptomatic patients and the incubation period infectivity in school outbreaks are analyzed, respectively. After the prevention and control measures are applied, the epidemic situation in each case will be controlled, and it will soon usher in a time when the epidemic situation improves. The research in this paper helps schools to select appropriate prevention and control measures, and accurately assess the impact of asymptomatic patients and incubation period infectivity on the epidemic.
-
Key words:
- cluster outbreak /
- COVID-19 /
- disease spread /
- effective distance /
- SEIR model
-
[1] 武汉市卫健委. 武汉市卫健委关于当前我市肺炎疫情的情况通报, 2019[EB/OL]. [2019-12-31]. http://wjw.wuhan.gov.cn/front/web/showDetail/2019123108989. The People’s Government of Wuhan Municipality. The current COVID-19 epidemic situation of Wuhan, 2019[EB/OL]. [2019-12-31]. http://wjw.wuhan.gov.cn/front/web/showDetail/2019123108989. [2] 陈端兵, 白薇, 王岩, 等. 新型冠状病毒肺炎防控效果的定量评估[J]. 电子科技大学学报, 2020, DOI: 10.12178/1001-0548.2020144. CHEN Duan-bing, BAI Wei, WANG Yan, et al. Quantitative evaluation of the prevention and control effects of COVID-19[J]. Journal of University of Electronic Science and Technology of China, 2020, DOI: 10.12178/1001-0548.2020144. [3] VIBOUD C, BOËLLE P Y, CAUCHEMEZ S, et al. Risk factors of influenza transmission in households[J]. British Journal of General Practice, 2004, 54(506): 684-689. [4] CAUCHEMEZ S, FERGUSON N M, WACHTEL C, et al. Closure of schools during an influenza pandemic[J]. The Lancet Infectious Diseases, 2009, 9(8): 473-481. [5] LITVINOVA M, LIU Q H, KULIKOV E S, et al. Reactive school closure weakens the network of social interactions and reduces the spread of influenza[J]. Proceedings of the National Academy of Sciences, 2019, 116(27): 13174-13181. [6] BROWN S T, TAI J H Y, BAILEY R R, et al. Would school closure for the 2009 H1N1 influenza epidemic have been worth the cost? A computational simulation of Pennsylvania[J]. Bmc Public Health, 2011, 11(1): 353. [7] PAN X, CHEN D, XIA Y, et al. Asymptomatic cases in afamily cluster with SARS-CoV-2 infection[J]. The Lancet Infectious Diseases, 2020, 20(4): 410-411. [8] BAI Y, YAO L, WEI T, et al. Presumed asymptomatic carrier transmission of COVID-19[J]. JAMA, 2020, DOI: 10.1001/jama.2020.2565. [9] 林俊锋. 基于引入隐形传播者的SEIR模型的COVID-19肺炎疫情分析和预测[J]. 电子科技大学学报, 2020, DOI: 10.12178/1001-0548.2020083. LIN Jun-feng. Assessment and prediction of COVID-19 based on SEIR model with undiscovered people[J]. Journal of University of Electronic Science and Technology of China, 2020, DOI: 10.12178/1001-0548.2020083. [10] 孙琬琬, 凌锋, 潘金仁, 等. 浙江省新型冠状病毒肺炎家庭聚集性疫情流行特征分析[J/OL]. (2020-03-15). 中华预防医学杂志, 2020, DOI: 10.3760/cma.j.cn112150-20200227-00199. SUN Wan-wan, LING Feng, PAN Jin-ren, et al. Epidemiological characteristics of 2019 novel coronavirus family clustering in Zhejiang Province[J/OL]. (2020-03-15). Chinese Journal of Preventive Medicine, 2020, DOI: 10.3760/cma.j.cn112150-20200227-00199. [11] QIU J. Covert coronavirus infections could be seeding new outbreaks[J]. Nature, 2020, DOI: 10.1038/d41586-020-00822-x. [12] DU Z, XU X, WU Y, et al. The serial interval of COVID-19 from publicly reported confirmed cases[J]. medRxiv, 2020, DOI: 10.1101/2020.02.19.20025452. [13] ZHANG Y Z, HOLMES E C. A genomic perspective on the origin and emergence of SARS-CoV-2[J]. Cell, 2020, DOI: 10.1016/j.cell.2020.03.035. [14] WANG R, CHEN F, CHEN Z, et al. StudentLife: Assessing mental health, academic performance and behavioral trends of college students using smartphones[C]//Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing. [S.l.]: ACM, 2014: 3-14. [15] ZHOU M, MA M, ZHANG Y, et al. EDUM: Classroom education measurements via large-scale WiFi networks[C]//Proceedings of the 2016 ACM International Joint Conference on Pervasive and Ubiquitous Computing. [S.l.]: ACM, 2016: 316-327. [16] CAO Y, GAO J, LIAN D, et al. Orderliness predicts academic performance: behavioural analysis on campus lifestyle[J]. Journal of the Royal Society Interface, 2018, 15(146): 20180210. [17] YAO H, LIAN D, CAO Y, et al. Predicting academic performance for college students: A campus behavior perspective[J]. ACM Transactions on Intelligent Systems and Technology (TIST), 2019, 10(3): 1-21. [18] The SocioPatterns Collaboration. Primary school temporal network data[DB/OL]. [2020-04-08]. http://www.sociopatterns.org/. [19] GEMMETTO V, BARRAT A, CATTUTO C. Mitigation of infectious disease at school: Targeted class closure vs school closure[J]. Bmc Infectious Diseases, 2014, 14(1): 695. [20] CATTUTO C, BROECK W V D, BARRAT A, et al. Dynamics of person-to-person interactions from distributed RFID sensor networks[J]. Plos One, 2010, 5(7): e11596. [21] 李靖, 李聪, 李翔. 人类时效交互网络的建模与传播研究综述[J]. 复杂系统与复杂性科学, 2019, 16(3): 1-21. LI Jing, LI Cong, LI Xiang. A Review on modeling and propagation of human temporal contact networks[J]. Complex Systems and Complexity Science, 2019, 16(3): 1-21. [22] 梁迪, 崔靖, 李翔. 线下交互的动态社交网络研究进展: 挑战与展望[J]. 计算机学报, 2018(7): 1598-1618. LIANG Di, CUI Jing, LI Xiang. A review on offline interaction in dynamical social networks: Challenge and prospect[J]. Chinese Journal of Computers, 2018(7): 1598-1618. [23] 范如国, 王奕博, 罗明, 等. 基于SEIR的新型肺炎传播模型及拐点预测分析[J]. 电子科技大学学报, 2020, DOI: 10.12178/1001-0548.2020029. FAN Ru-guo, WANG Yi-bo, LUO Ming, et al. SEIR-based novel pneumonia transmission model and inflection point prediction analysis[J]. Journal of University of Electronic Science and Technology of China, 2020, DOI: 10.12178/1001-0548.2020029. [24] ANDERSON R M, ANDERSON B, MAY R M. Infectious diseases of humans: dynamics and control[M]. Oxford: Oxford University Press, 1992. [25] GUAN W, NI Z, HU Y, et al. Clinical characteristics of coronavirus disease 2019 in China[J]. New England Journal of Medicine, 2020, DOI: 10.1056/NEJMoa2002032. [26] WANG Da-wei, HU Bo, HU Chang, et al. Clinical characteristics of 138 hospitalized patients with 2019 novel coronavirus-infected pneumonia in Wuhan, China[J]. Jame the Journal of the American Medical Association, 2020, 323(11): 1061-1069. [27] BROCKMANN D, HELBING D. The hidden geometry of complex, network-driven contagion phenomena[J]. Science, 2013, 342(6164): 1337-1342. [28] ROSSANA M, JULIE F, ALAIN B, et al. Contact patterns in a high school: a comparison between data collected using wearable sensors, contact diaries and friendship surveys[J]. Plos One, 2015, 10(9): e0136497. -


 ISSN
ISSN 




 下载:
下载: