随着信息技术的飞速发展，人们对身份认证的可靠度和方式提出了新的要求，传统的身份认证技术已经不能满足人们的需求^[1]。作为生物特征识别技术的一种，人脸识别因其符合人类自身的生理视觉习惯，是用户接受度最高的生物识别方式。

二维人脸识别经过多年的发展已经能够获得高识别率，但是单纯依靠二维图像信息的人脸识别存在诸多难题(如表情、姿势和光照等)，在应用各方面遭受到了巨大的挑战。而三维人脸识别比二维人脸识别有着显著的优势，首先三维人脸富含海量信息；其次，有研究证明三维人脸识别技术使用的形状信息能够更好地应对光照和姿势的挑战。同时随着硬件(存储、计算等设备)的飞速发展以及三维数据采集技术的迅猛发展，越来越多的学者将目光投向了三维人脸识别的研究。完整的三维人脸识别系统主要包括数据采集、预处理、特征提取和匹配，根据匹配结果得出识别结果。三维人脸匹配是最关键的步骤，直观地说就是目标人脸与模型人脸的匹配，根据匹配结果判断是否所需人脸。常用的三维人脸匹配方法有基于整体特征^{[2, 3, 4]}、基于局部特征^{[5, 6, 7]}、基于空域信息^[8]、基于深度图^{[9, 10]}和双模态融合^[11]，其中基于深度图的匹配是应用最广泛的方法。深度图是三维人脸的主要表达方式，能够有效避免光照的影响，表示的是深度信息z。常见的方法如ICP、遗传算法和模拟退火算法等。本文基于模拟退火算法，选取合适的适应度函数——MLESAC和SIM，利用三维人脸的深度信息进行匹配，经过测试验证，展现了高识别率。

模拟退火算法(SA)^[12]是一种常用的优化算法，通过给予整个搜索过程一个时变且最后趋向零的概率突变性，跳出了局部最优解而具有了全局最优解。SA包括两重循环：参数的随机扰动和温度降低。在初始时给出一个试探解，然后在领域中随机产生另一个解，该新解要满足Metropolis所提出的规则限制，而整个变化过程都由控制参数t所决定。对于t的每一次取值，SA都不断进行“产生-判断-接受(或舍去)”的多次迭代，当t逐渐减小并逐渐趋向于0时的系统状态对应优化问题的全局最优解。

随机抽样最大似然(MLESAC)算法由文献^[13]提出，被广泛地应用于估计三维图像匹配过程中产生的内外点，从而得到最优匹配点。

通过基于MLESAC的孤立点分类方法定义适应度函数为：

曲面渗透测度(SIM)^[14]基于每个点的曲面法向量定量匹配结果，计算出两幅图像的对应点集 $C(A,B)$后，通过计算 ${\rm{SIM}}(A,B) = \frac{{|C(A,B)|}}{{|A|}}$控制匹配 流程和识别结果。SIM的具体步骤如下：

1) 对于A中的点p定义一个nxn的邻域点集；

2) 寻找p在B中的匹配点c；

3) 计算点p和点c处的法向量 ${n_p}$和 ${n_c}$；

4) 计算 ${n_p}$和 ${n_c}$的夹角θ；

5) 如果 $\theta < m$，且在 ${n_p}$中存在不相等的两点 ${q_i}$和 ${q_j}$，同时 ${q_{\rm{i}}},{q_j}$能够被点c处的切平面分割开，那么就把该点归入对应点集 $C(A,B)$中；

6) 重复步骤1)～步骤5)，直到A中所有点都计算完毕。

一个好的匹配拥有较高的SIM值，而误差匹配则产生较低的SIM值。误差匹配时SIM值与值之间的差异相较于MSE更大，即SIM更敏感。但是，SIM只有在已经进行了粗略匹配时才能够展现其优势。

在三维人脸匹配中，由于图像维数较高，数据信息量大而导致计算量巨大，从而引发识别速度慢。为此，采用了“由粗到细”(coarse to fine)的策略，分两步或多步匹配图像。

如图 1所示，利用模拟退火算法进行匹配主要分3步：1) 基于重心的初始匹配；2) 基于MLESAC的SA粗略匹配；3) 基于SIM的SA精准匹配。具体来说，首先利用重心对齐，把两幅人脸转换到相同的坐标系；再利用MLESAC作为适应度函数进行粗略匹配，找出对应点；最后通过更精细的方法，采用SIM作为适应度函数选取更准确的对应点，并以SIM值作为识别依据对人脸进行判定。三维人脸识别的判断基于两个阈值：1) 识别阈值；2)拒绝阈值。如果计算结果高于识别阈值，人脸被认定是相互匹配的；如果结果低于拒绝阈值，则被认定是不相互匹配的。

图1

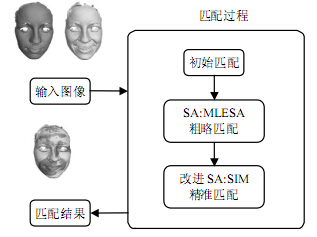图1基于模拟退火算法的三维人脸匹配流程

三维人脸识别的一个难点就是表情的存在。当进行带表情人脸VS不带表情人脸的匹配时，无论匹配与否得到的SIM值都较低，于是很难得到一个精准的匹配结果。针对这个难点，提出一个改进的精准匹配过程。

图 2中，图 2a是没有改进时所使用的整张人脸区域；图 2b是通过眼角、鼻翼、鼻尖特征点划分的9块人脸区域；图 2c中亮区域表示改进后所使用的刚性区域。在没有改进的精准匹配过程中，SIM的值通过计算所有的匹配点得到。在本文改进的精准匹配过程中，通过权值对刚性区域投以更多的关注，对于不变区域的匹配点给定高权值(如，w=500)；对于变化区域的匹配点给定低权值(如，w=0)。当然，最后计算SIM值时，所有匹配点的权值均为w=1。

图2

图2三维人脸区域划分

大部分三维人脸识别都是使用整张人脸进行识别判定，或者为了避免表情的影响仅仅使用刚性区域进行识别判定。有些学者也通过选择不同分类器整合不同的区域进行识别判定，如乘积规则、求和规则等，但文献^[15]证明求和规则比其他的组合分类器更优秀。

为了得到最佳识别结果，本文使用求和规则组合所有区域的SIM值，即C+E+U+F+M得到最后的SIM值来进行识别。在实验中，通过求和规则整合所有区域得到的识别率达到了99.2%，而其他的整合区域，如C+E+U+F只达到了98.9%，甚至有U+M仅仅达到了86.7%的识别率。

在整个精准匹配的过程中，利用模拟退火算法作为搜索对应点的迭代算法；同时利用SIM作为适应度函数来得到最终的对应点集；最后计算最终对应点集的SIM值作为三维人脸识别的依据。根据SIM算法流程、模拟退火算法流程以及本文提出的改进，实现该阶段整个匹配过程的具体步骤如下：

1) 获取目标和模型人脸各个人脸区域粗略匹配后的点集，包括5个区域：鼻子圆形区域C、鼻子椭圆区域E、面部区域上半部分U、整个面部区域F、基于改进SA的面部区域M；

2) 初始化参数；

3) 产生新解；

4) 计算新旧参数下，目标人脸与模型人脸的对应点集；

5) 根据对应点集计算函数差值；

6) 根据模拟退火的各种收敛条件判断是否接受新解；

7) 同一温度下，重复执行两次步骤3)～步骤6)；

8) 缓慢降低温度t，直至达到收敛条件为止，即步骤3)～步骤7)；

9)得出各个人脸区域的最终坐标变换，并根据SIM得到相应的对应点集，计算各个人脸区域的 SIM值；

10) 利用求和规则总和各个区域C+E+U+F+M的值，并以此为依据与阈值相比较得出识别结果。

精准匹配阶段，利用SIM作为适应度函数进行更精准的匹配，通过匹配后得到的SIM值来判断获得最后的识别结果：如果两幅图像均来自同一个人，匹配后会得到较高的SIM值；否则，将会得到一个较低的SIM值。

为了验证算法的健壮性和精准性，分别进行verification实验、identification实验和增加迭代次数的实验。首先进行数据集的分类。

本文实验采用3D_RMA数据库，共计120副人脸，每个人脸有6副图像，这些人脸都有正面人脸图像并且具有不同的表情。最常见的表情是：无表情、笑、悲伤、讨厌、惊讶。根据图像是否带噪声或者表情把三维人脸数据库分成4个数据集，数据集的识别难度逐步递增，具体分类如表 1所示。

表1

表1 数据集分类

表1 数据集分类 数据集 描述 人脸数量/副 Level0 不带表情且无噪声人脸 28 Level1 不带表情人脸 65 Level2 无噪声人脸 79 All 数据库中所有人脸 120

参照表 1所展示的各数据集，定义其中的一个数据集为gallery数据集，那么其他的数据集就作为probe数据集，实验通过匹配gallery和probe数据集进行，实验结果如表 2所示。表 2的前两列分别表示相应的gallery和probe数据集，后一列展示了各个数据集的识别率。而图 3和图 4则是三维人脸匹配的两个示例。其中，图a表示模型人脸，即位于gallery数据集中的人脸数据；图b表示待匹配人脸，即位于probe数据集中的人脸数据；图c表示两幅人脸匹配后的效果图，表现为一个“相互渗透”的效果。

图 3是来自相同三维人脸的匹配示例图，其中，图 3a是中性表情人脸，而图 3b是带了微笑的表情；图 4是来自不同三维人脸的匹配示例图，两幅人脸都是中性表情人脸。

表2

表2 verification识别率

表2 verification识别率 gallery probe 识别率/% Level0 Level0 96.4 Level0 Level1 96.9 Level0 Level2 96.2 Level0 All 90.8 Level1 All 83.3 All All 70.8

图3

图3相同三维人脸匹配示例

图4

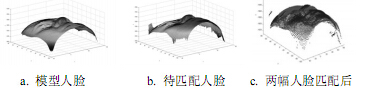图4不同三维人脸匹配示例

从定性角度可以看到图 3的“相互渗透”比较多，尤其在下半部人脸，图 4中几乎没有表现出“相互渗透”的区域。而从定量角度的SIM值来看，实验所得的图 3的SIM值比图 4的高。从这里也可以看到本文的方法对中性表情VS带表情人脸时，具有较好的识别效果。

表 2的实验结果表明，当人脸带有表情和噪声时，人脸数据会发生相应的变化，从而增加识别的难度。而从表中的实验数据也可以看到本文的识别率也不高，尤其是最后的All VS All实验，只达到了70.8%的结果。

但是在实验中可以发现，在进行带表情人脸VS中性人脸的匹配时，改进方法比原始方法更优秀，高了几乎15%的识别率。

不同于verification实验，在identification实验中，定义4个gallery数据集：

1) Level0：28副人脸；2) Level1：65副人脸；3) First：挑选数据库中每个人的第一幅人脸，共计20副人脸；4) All：120副人脸。

其中Level0和Level1是verification实验中的Level0和Level1。对应每个gallery数据集的probe数据集则是包含了该gallery数据集剩下后的所有人脸。

通过观察表 3的实验结果，本文使用的方法在rank-1的识别下仍然取得了较高的识别率。而表 3中的最后一行，与verification实验一样，同样是进行了All VS All的实验，probe中的每幅人脸都同剩余人脸相匹配，确认每幅人脸的身份，获得了高达98.3%的识别率。在所有数据集的识别中，All VS All的实验获得最高的识别率，是因为一个人可能有多幅人脸被归类在gallery数据集中，增大了确认身份的机会。

表3

表3 identification实验：rank-1的识别率

表3 identification实验：rank-1的识别率 gallery probe rank-1的识别率/% Level 0 Others 96.7 Level 1 Others 96.4 First Others 98.0 All All 98.3

在SA匹配过程中，通过限制迭代次数K减少执行时间，提高执行效率。规定当某一解迭代了K=200次后都没发生变化时，结束匹配过程，称该解为最优解。但是，究竟迭代次数对识别率有没有影响？本文通过增加迭代次数K进行了相关实验，希望能够找出迭代次数对识别率是否有没有影响，或者有多大的影响，能够提高多大幅度的识别率。在实验中，为了检验增加迭代次数是否能够提高识别率，同时也为了提高效率，并没有对所有的SA识别过程都增加K值，而是只有当人脸被错误接受或者错误拒绝时，才增加K为2 000。

表 4展示了增加迭代次数后，verification实验和rank-1下identification实验的识别率。通过观察发现，在SA的搜索过程中，通过增加迭代次数K可以提高识别率。但是相应的，会增加匹配所需的时间成本。

表4

表4 增加迭代次数实验

表4 增加迭代次数实验 实验 数据集 识别率/% verification Level0VS Level0 100.0 Level0VS Level1 100.0 Level0VS Level2 98.7 Level0 VS All 99.2 Level1 VS All 98.3 All VS All 97.5 identification(rank-1) Level0 VS Others 98.9 Level1 VS Others 98.2 First VS Others 99.0 All VS All 99.2

以上所有的实验结果表明，SIM在三维人脸识别中是一个很好的适应度函数，不仅对识别结果敏感，还能对整个识别过程进行控制。同时，也验证了分阶段进行匹配和改进方法的健壮性和精准性。

通过上面的分析以及实验结果可以得出以下结论：1) SA开辟了求解组合优化问题的新途径，与其他局部搜索算法(如爬山算法)的最大区别在于，SA能够在迭代过程中接受更糟的解决方案。就是因为这个不同点，SA并不趋向于局部最小，而能够无限接近于全局最优解。2) 通过选择正确的人脸区域能够有效克服表情带来的影响，提高识别率。3)通过选择正确的分类器能够提高识别率。4)提出的改进方法对带表情人脸VS不带表情人脸的匹配获得高识别率，但是对带表情人脸VS带表情人脸的匹配无法获得良好的效果，仍需进一步加强对人脸表情处理方法的研究。