弹载合成孔径雷达(synthetic aperture radar, SAR)已成为近年来SAR成像领域的研究热点之一。弹载SAR导引头通过实时获取的SAR图像与弹上数据库中的基准图像进行匹配,再由几何关系解算导弹位置坐标,能够达到提高制导精度的目的[1]。由于导弹重量、体积的限制,及其作战运用的特殊性,其对SAR系统的重量、体积及成本等也提出了更高的要求。
调频连续波(frequency modulated continuous wave, FMCW)SAR与传统的脉冲式SAR相比,具有体积小、重量轻、成本低、功耗低等优势[2, 3]。接收端采用去调频(dechirp)处理体制,回波信号与参考信号进行混频,产生较小的差频带宽,能够降低对视频接收通道、后端A/D采集设备和信号处理速度的要求[4]。同时,FMCW雷达很大的时宽带宽积,使其难以被传统的侦察机截获,具有良好的低截获概率[5]。这些特点使其更适合应用于弹载平台[6, 7]。
通常导弹在攻击目标时,FMCW SAR工作在俯冲模式,即存在一定的径向速度及加速度[8]。在俯冲运动状态下,由于平台运动形式的复杂性,常规的FMCW SAR成像方法不能直接应用于俯冲弹载FMCW SAR成像中[9, 10, 11]。同时,由于弹载SAR对数据处理的实时性要求较高,在设计成像方法时,应在保证分辨率的基础上尽量减少成像处理步骤及运算量。文献[12]提出了一种俯冲运动状态下弹载FMCW SAR成像方法,重点对导弹径向速度及加速度引起的剩余二次相位误差进行补偿,解决了距离像散焦问题。但是,该方法仅对目标斜距表达式进行二阶近似,当成像分辨率较高,导弹斜距历程变化较大时,这种近似并不能满足成像需求。
针对弹载FMCW SAR俯冲运动状态下的特点,本文首先分析了弹载FMCW SAR成像几何关系,在时域完成距离走动校正之后,进一步地采用级数反演的方法推导了弹载FMCW SAR回波差频信号的精确方位多普勒频域表达式,通过对方位多普勒频域表达式进行分析,提出了一种弹载FMCW SAR俯冲成像方法。点目标及场景目标仿真实验验证了该方法的有效性。
1 弹载FMCW SAR几何模型
弹载FMCW SAR俯冲成像几何示意图如图 1所示,  为导弹的飞行轨迹,在地面的投影为X轴。设t=0时刻,导弹位于B点,高度为h。导弹沿X轴方向速度分量为vx,加速度为ax,沿Y轴方向的速度分量为vy,加速度为ay,θ0表示导弹在B点时的斜视角。
为导弹的飞行轨迹,在地面的投影为X轴。设t=0时刻,导弹位于B点,高度为h。导弹沿X轴方向速度分量为vx,加速度为ax,沿Y轴方向的速度分量为vy,加速度为ay,θ0表示导弹在B点时的斜视角。
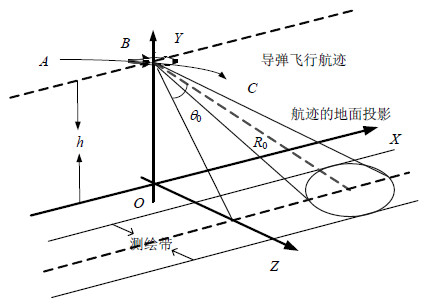 |
| 图1俯冲运动状态下弹载FMCW SAR成像几何模型 |
成像场景中一目标点的坐标为(X0,0,Z0),且X0可表示为X0=Xc+Xn,其中,Xc为场景中心点横坐标,Xn表示目标点方位向位置。由于FMCW信号是在一个脉冲持续时间内连续的发射信号,且脉冲持续时间较长,传统的脉冲式SAR所采用的“一步一停”工作模式不再适用,需考虑导弹飞行过程中与目标之间距离的脉内变化。因此,目标瞬时斜距应表示为:
| $ \begin{array}{l} R({t_{\rm{k}}},{t_{\rm{m}}}) = \left( {{{\left( {{X_0} - {v_x}({t_{\rm{k}}} + {t_{\rm{m}}}) - \frac{1}{2}{a_x}{{({t_{\rm{k}}} + {t_{\rm{m}}})}^2}} \right)}^2}} \right. + \\ \;\;\;\;\;{\left. {{{\left( {h + {v_y}({t_{\rm{k}}} + {t_{\rm{m}}}) + \frac{1}{2}{a_y}{{({t_{\rm{k}}} + {t_{\rm{m}}})}^2}} \right)}^2} + Z_0^2} \right)^{\frac{1}{2}}} \end{array} $ | (1) |
式中,tk表示快时间;tm表示慢时间。将式(1)在tk处展开为一阶泰勒级数[12]:
| $R({t_{\rm{k}}},{t_{\rm{m}}}) \approx R({t_{\rm{m}}}) + \alpha {t_{\rm{k}}}$ | (2) |
式中, $ R({t_{\rm{m}}}) = \sqrt {R_0^2 + {\alpha _1}{t_{\rm{m}}} + {\alpha _2}t_{\rm{m}}^2 + {\alpha _3}t_{\rm{m}}^{\rm{3}} + {\alpha _4}t_{\rm{m}}^{\rm{4}}} $, $ {\alpha _1} = - 2{X_0}{v_x} + 2h{v_y}$, $ {\alpha _2} = v_x^2 - {X_0}{a_x} + v_y^2 + h{a_y}$, $ {\alpha _3} = {v_y}{a_y} + {v_x}{a_x}$, $ {\alpha _4} = \frac{1}{4}a_y^2 + \frac{1}{4}a_x^2$, $ {R_0} = \sqrt {X_0^2 + {h^2} + Z_0^2} $, $\alpha = {\rm{d}}R\left( {{t_{\rm{k}}},{t_{\rm{m}}}} \right)/{\rm{d}}{t_{\rm{k}}}{|_{{t_{\rm{k}}}}} = 0$。
由R(tm)的表达式可以看出,导弹俯冲运动状态下运动形式较为复杂,根号内包含了关于慢时间tm的四次项,将R(tm)进一步展开为tm的幂级数,并且需保留到tm的四次项:
| $R({t_m}) \approx {R_0} + {\mu _1}{t_{\rm{m}}} + {\mu _2}t_{\rm{m}}^2 + {\mu _3}t_{\rm{m}}^3 + {\mu _4}t_{\rm{m}}^4$ | (3) |
式(3)中关于慢时间tm的一次项为线性距离走动项,在成像处理中,应首先对线性距离走动进行校正。为便于后续的处理,一次项系数可进一步表示为:
| ${\mu _1} = \frac{{{\alpha _1}}}{{2{R_0}}} = \frac{{ - {X_0}{v_x} + h{v_y}}}{{{R_{\rm{s}}} + {X_n}\sin {\theta _0}}} = - {v_x}\sin {\theta _0} + \frac{{{v_y}h}}{{{R_{\rm{s}}}}} + \rho {X_n} $ | (4) |
假设雷达发射FMCW信号,接收端经dechirp处理后,回波差频信号可表示为:
| $ \begin{array}{l} {s_{{\rm{if}}}}({t_{\rm{k}}},{t_{\rm{m}}}) = \exp \left( { - {\rm{j}}\left( {\frac{{4{\rm{\pi }}}}{c}\mu \left( {{t_{\rm{k}}} - \frac{{2{R_{{\rm{ref}}}}}}{c}} \right){R_\Delta }} \right)} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\exp \left( { - {\rm{j}}\left( {\frac{{4{\rm{\pi }}}}{\lambda }{R_\Delta } - \frac{{4{\rm{\pi }}\mu }}{{{c^2}}}R_\Delta ^2} \right)} \right) \end{array} $ | (5) |
| ${s_{{\rm{if}}}}(\Delta {K_{\rm{R}}},{t_{\rm{m}}}) = \exp ( - {\rm{j}}{K_{\rm{R}}}{R_\Delta }) \otimes \exp \left( { - {\rm{j}}\frac{{\Delta K_{\rm{R}}^2}}{{2b}}} \right)$ | (6) |
式中,${K_{\rm{R}}} = {K_{{\rm{Rc}}}} + \Delta {K_{\rm{R}}}({t_{\rm{k}}})$;$\Delta {K_{\rm{R}}} = \frac{{4{\rm{\pi }}\mu }}{c}\left( {{t_{\rm{k}}} - \frac{{2{R_{{\rm{ref}}}}}}{c}} \right)$;${K_{{\rm{Rc}}}} = \frac{{4{\rm{\pi }}{f_c}}}{c}$;$b = \frac{{8{\rm{\pi }}\mu }}{{{c^2}}}$;$ \otimes $为卷积符号;最后一个指数项为剩余视频相位(RVP)项,可在方位多普勒频域完成补偿[13]。
经RVP项补偿后,进一步构造距离走动补偿函数在时域对距离走动进行补偿,补偿函数为:
| ${H_{{\rm{walk}}}} = \exp ( - {\rm{j}}{K_{\rm{R}}}{L_{\rm{R}}}{t_{\rm{m}}})$ | (7) |
经距离走动校正后,回波差频信号可表示为:
| $ {s'_{{\rm{if}}}}(\Delta {K_{\rm{R}}},{t_{\rm{m}}}) = \exp ( - {\rm{j}}{K_{\rm{R}}}({R_\Delta } + {L_{\rm{R}}}{t_{\rm{m}}})) $ | (8) |
对式(8)进行方位向的傅里叶变换:
| $ \begin{array}{c} {S_{{\rm{if}}}}(\Delta {K_{\rm{R}}},{f_a}) = \int_{{\rm{ }} - \infty }^{{\rm{ }} + \infty } {{{s'}_{{\rm{if}}}}(\Delta {K_{\rm{R}}},{t_{\rm{m}}}) \cdot \exp ( - {\rm{j}}2{\rm{\pi }}{f_a}{t_{\rm{m}}}){\rm{d}}{t_{\rm{m}}}} = \\ \int_{{\rm{ }} - \infty }^{{\rm{ }} + \infty } {\exp ( - {\rm{j}}2{\rm{\pi }}{f_a}{t_{\rm{m}}})} \times \\ \exp ( - {\rm{j}}{K_{\rm{R}}}(R({t_{\rm{k}}},{t_{\rm{m}}}) - {R_{{\rm{ref}}}} + {L_{\rm{R}}}{t_{\rm{m}}})){\rm{d}}{t_{\rm{m}}} \end{array} $ | (9) |
作变量代换$t = {t_{\rm{k}}} + {t_{\rm{m}}}$,则上式可进一步表示为:
| $ \begin{array}{c} {S_{{\rm{if}}}}(\Delta {K_{\rm{R}}},{f_a}) = \int_{{\rm{ }} - \infty }^{{\rm{ }} + \infty } {\exp ( - {\rm{j}}2{\rm{\pi }}{f_a}(t - {t_{\rm{k}}}))} \times \\ \exp ( - {\rm{j}}{K_{\rm{R}}}(R(t) - {R_{{\rm{ref}}}} + {L_{\rm{R}}}(t - {t_{\rm{k}}}))){\rm{d}}t = \\ \exp ({\rm{j}}({K_{\rm{R}}}{L_{\rm{R}}}{t_{\rm{k}}} + 2\pi {f_a}{t_{\rm{k}}})) \times \\ \int_{ - \infty }^{ + \infty } {\exp ( - {\rm{j}}2{\rm{\pi }}{f_a}t)} \exp ( - {\rm{j}}{K_{\rm{R}}}(R(t) - {R_{{\rm{ref}}}} + {L_{\rm{R}}}t)){\rm{d}}t \end{array} $ | (10) |
| $ \begin{array}{c} {S_{{\rm{if}}}}(\Delta {K_R},{f_a}) = \exp ({\rm{j}}({K_{\rm{R}}}{L_{\rm{R}}}{t_{\rm{k}}} + 2{\rm{\pi }}{f_a}{t_{\rm{k}}})) \times \\ \int_{{\rm{ }} - \infty }^{{\rm{ }} + \infty } {\exp ( - {\rm{j}}2{\rm{\pi }}{f_a}{t_{\rm{m}}})} \exp ( - {\rm{j}}{K_{\rm{R}}}(R({t_{\rm{m}}}) - {R_{{\rm{ref}}}} + {L_{\rm{R}}}{t_{\rm{m}}})){\rm{d}}{t_{\rm{m}}} \end{array} $ | (11) |
| $ \frac{{{\rm{d}}( - {K_{\rm{R}}}(R({t_{\rm{m}}}) - {R_{{\rm{ref}}}} + {L_{\rm{R}}}{t_{\rm{m}}}))}}{{{\rm{d}}{t_{\rm{m}}}}} - 2{\rm{\pi }}{f_a} = 0 $ | (12) |
| $ - {\mu _1}' - 2{\mu _2}t_{\rm{m}}^* - 3{\mu _3}t_{\rm{m}}^{*2} - 4{\mu _4}t_{\rm{m}}^{*3} = \frac{{2\pi {f_a}}}{{{K_R}}}$ | (13) |
| $\begin{array}{l} t_{\rm{m}}^{\rm{*}}({f_a}) = - \frac{{{\beta _1}}}{{{K_{\rm{R}}}}}\left( {{f_a} + \frac{{{{\mu '}_1}{K_R}}}{{2{\rm{\pi }}}}} \right) - \frac{{{\beta _2}}}{{K_{\rm{R}}^2}}{\left( {{f_a} + \frac{{{{\mu '}_1}{K_R}}}{{2{\rm{\pi }}}}} \right)^2} - \\ \;\;\;\;\;\;\;\frac{{{\beta _3}}}{{K_{\rm{R}}^3}}{\left( {{f_a} + \frac{{{{\mu '}_1}{K_R}}}{{2{\rm{\pi }}}}} \right)^3} - \frac{{{\beta _4}}}{{K_{\rm{R}}^4}}{\left( {{f_a} + \frac{{{{\mu '}_1}{K_R}}}{{2{\rm{\pi }}}}} \right)^4} \end{array}$ | (14) |
将式(14)代入式(11),可得回波差频信号的方位多普勒域表达式为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;{S_{{\rm{if}}}}(\Delta {K_{\rm{R}}},{f_a}) = \exp ({\rm{j}}\phi (\Delta {K_{\rm{R}}},{f_a})) \times \\ \exp ({\rm{j}}({K_{{\rm{Rc}}}}{L_{\rm{R}}}{t_{\rm{k}}} + 2\pi {f_a}{t_{\rm{k}}})){\rm{ }}\exp ({\rm{j}}\Delta {K_{\rm{R}}}{L_{\rm{R}}}{t_{\rm{k}}}) \end{array} $ | (15) |
| $ \begin{array}{l} \phi (\Delta {K_{\rm{R}}},{f_a}) = - {K_{\rm{R}}}({R_0} - {R_{{\rm{ref}}}}) + \frac{{{\rm{\pi }}{\beta _1}}}{{{K_{\rm{R}}}}}{\left( {{f_a} + \frac{{{{\mu '}_1}{K_R}}}{{2{\rm{\pi }}}}} \right)^2} + \\ \;\;\frac{{{\rm{2\pi }}{\beta _2}}}{{3K_{\rm{R}}^2}}{\left( {{f_a} + \frac{{{{\mu '}_1}{K_R}}}{{2{\rm{\pi }}}}} \right)^3} + \frac{{{\rm{\pi }}{\beta _3}}}{{2K_{\rm{R}}^3}}{\left( {{f_a} + \frac{{{{\mu '}_1}{K_R}}}{{2{\rm{\pi }}}}} \right)^4} \end{array} $ | (16) |
式(15)中后两个指数项是俯冲下降段弹载FMCW SAR所特有的,分别为导弹连续运动引起的多普勒频移项和剩余二次相位项。在方位多普勒频域构造补偿函数对多普勒频移和剩余二次相位进行补偿,补偿函数分别为:
| ${H_{\rm{D}}} = \exp ({\rm{j}}({K_{{\rm{Rc}}}}{L_{\rm{R}}}{t_{\rm{k}}} + 2{\rm{\pi }}{f_a}{t_{\rm{k}}}))$ | (17) |
| ${H_{{\rm{DD}}}} = \exp ({\rm{j}}\Delta {K_{\rm{R}}}{L_{\rm{R}}}{t_{\rm{k}}})$ | (18) |
下面对式(15)的相位$\phi ({t_{\rm{k}}},{f_a})$进行分析,将相位$\phi ({t_{\rm{k}}},{f_a})$在$\Delta {K_{\rm{R}}} = 0$处作泰勒级数展开:
| $ \begin{array}{c} \phi (\Delta {K_{\rm{R}}},{f_a}) = - {K_{\rm{R}}}({R_s} + {X_n}\sin {\theta _0} - {R_{{\rm{ref}}}}) + 2{\rm{\pi }}\eta {f_a} + \\ \left( {\frac{{{\rm{\pi }}{\beta _1}}}{{{K_{{\rm{Rc}}}}}} - \frac{{{\rm{\pi }}{\beta _1}}}{{K_{{\rm{Rc}}}^2}}\Delta {K_{\rm{R}}} + \frac{{{\rm{\pi }}{\beta _1}}}{{K_{{\rm{Rc}}}^3}}\Delta K_{\rm{R}}^2} \right)f_a^2 + \\ \left( {\frac{{2{\rm{\pi }}{\beta _2}}}{{3K_{{\rm{Rc}}}^2}} - \frac{{4{\rm{\pi }}{\beta _2}}}{{3K_{{\rm{Rc}}}^{\rm{3}}}}\Delta {K_R} + \frac{{2{\rm{\pi }}{\beta _2}}}{{K_{{\rm{Rc}}}^{\rm{4}}}}\Delta K_{\rm{R}}^{\rm{2}}} \right)f_a^3 + \\ \left( {\frac{{{\rm{\pi }}{\beta _3}}}{{2K_{{\rm{Rc}}}^{\rm{3}}}} - \frac{{3{\rm{\pi }}{\beta _3}}}{{2K_{{\rm{Rc}}}^{\rm{4}}}}\Delta {K_{\rm{R}}} + \frac{{3{\rm{\pi }}{\beta _3}}}{{K_{{\rm{Rc}}}^{\rm{5}}}}\Delta K_{\rm{R}}^{\rm{2}}} \right)f_a^4 \end{array} $ | (19) |
由此,回波差频信号方位多普勒频域表达式可写为:
| $ \begin{array}{c} {S_{{\rm{if}}}}(\Delta {K_{\rm{R}}},{f_a}) = \exp ( - {\rm{j}}{K_{\rm{R}}}({R_0} - {R_{{\rm{ref}}}})) \times \\ \exp \left( {{\rm{j}}\left( {2{\rm{\pi }}\eta {f_a} + \frac{{{\rm{\pi }}{\beta _1}f_a^2}}{{{K_{{\rm{Rc}}}}}}} \right)} \right) \times \\ {\rm{exp}}\left( {{\rm{j}}\left( {\frac{{2{\rm{\pi }}{\beta _2}f_a^3}}{{3K_{{\rm{Rc}}}^2}} + \frac{{{\rm{\pi }}{\beta _3}f_a^4}}{{2K_{{\rm{Rc}}}^{\rm{3}}}}} \right)} \right) \times \\ {\rm{exp}}\left( {{\rm{j}}\left( {\frac{{{\rm{\pi }}{\beta _1}f_a^2}}{{K_{{\rm{Rc}}}^2}} - \frac{{4{\rm{\pi }}{\beta _2}f_a^3}}{{3K_{{\rm{Rc}}}^{\rm{3}}}} - \frac{{3{\rm{\pi }}{\beta _3}f_a^4}}{{2K_{{\rm{Rc}}}^{\rm{4}}}}} \right)\Delta {K_{\rm{R}}}} \right) \times \\ {\rm{exp}}\left( {{\rm{j}}\left( {\frac{{{\rm{\pi }}{\beta _1}f_a^2}}{{K_{{\rm{Rc}}}^3}} + \frac{{2{\rm{\pi }}{\beta _2}f_a^3}}{{K_{{\rm{Rc}}}^{\rm{4}}}} + \frac{{3{\rm{\pi }}{\beta _3}f_a^4}}{{K_{{\rm{Rc}}}^{\rm{5}}}}} \right)\Delta K_{\rm{R}}^{\rm{2}}} \right) \end{array} $ | (20) |
1) 方位调制补偿函数:
| ${H_{{\rm{FM}}}} = \exp \left( { - {\rm{j}}\left( {\frac{{2{\rm{\pi }}{\beta _2}}}{{3K_{{\rm{Rc}}}^2}}f_a^3 + \frac{{{\rm{\pi }}{\beta _3}}}{{2K_{{\rm{Rc}}}^{\rm{3}}}}f_a^4} \right)} \right)$ | (21) |
2) 距离徙动校正函数:
| ${H_{{\rm{RMC}}}} = \exp \left( { - {\rm{j}}\left( {\frac{{{\rm{\pi }}{\beta _1}f_a^2}}{{K_{{\rm{Rc}}}^2}} - \frac{{4{\rm{\pi }}{\beta _2}f_a^3}}{{3K_{{\rm{Rc}}}^{\rm{3}}}} - \frac{{3{\rm{\pi }}{\beta _3}f_a^4}}{{2K_{{\rm{Rc}}}^{\rm{4}}}}} \right)\Delta {K_{\rm{R}}}} \right)$ | (22) |
3) 二次距离压缩函数:
| ${H_{{\rm{SRC}}}} = \exp \left( { - {\rm{j}}\left( {\frac{{{\rm{\pi }}{\beta _1}f_a^2}}{{K_{{\rm{Rc}}}^3}} + \frac{{2{\rm{\pi }}{\beta _2}f_a^3}}{{K_{{\rm{Rc}}}^{\rm{4}}}} + \frac{{3{\rm{\pi }}{\beta _3}f_a^4}}{{K_{{\rm{Rc}}}^{\rm{5}}}}} \right)\Delta K_{\rm{R}}^{\rm{2}}} \right)$ | (23) |
完成上述距离徙动校正和二维去耦两步补偿后,对回波差频信号作快时间的傅里叶变换,进行距离压缩,然后在距离—多普勒域进行方位脉压,方位脉压函数为:
| ${H_{{\rm{AREF}}}} = \exp \left( { - {\rm{j}}\frac{{{\rm{\pi }}{\beta _1}}}{{{K_{{\rm{Rc}}}}}}f_a^2} \right)$ | (24) |
将式(24)和完成距离压缩的信号相乘,并进行方位向傅里叶逆变换,即完成了方位向压缩,经几何形变校正处理后,最终获得理想的FMCW SAR二维图像。整个算法处理流程如图 2所示。
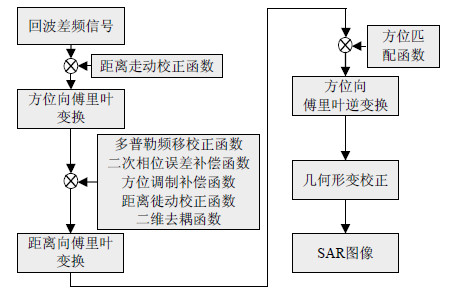 |
| 图2成像处理流程图 |
与文献[12]相比,本文通过构造不同的补偿函数来实现更高精度的成像,却并没有增加额外的运算量。
3 仿真分析与验证导弹各项运动参数为:飞行高度h=10 km,水平飞行速度vx=1 000 m/s,加速度ax=-30 m/s2,径向速度vv=-200 m/s,加速度av=-30 m/s2。弹载FMCW SAR雷达载频为35 GHz(波长为0.0086 m),脉冲持续时间0.2 ms,带宽为300 MHz,采样频率1.2 MHz,作用距离为25 km,场景宽度200 m,合成孔径长度约为350 m。
在上述参数配置情况下,不同近似程度的斜距误差如图 3所示。由图 3的对比可以看出,在一个合成孔径时间内,对斜距进行二阶近似的误差较大,最大误差达到了0.005 m,超过了波长的1/4。显然,对斜距进行二阶近似时不满足成像要求。而对斜距进行三阶和四阶近似时,最大误差都远小于波长的1/4,能够满足成像的需求。对于仿真中给出的参数,要想得到聚焦良好的图像,至少要对斜距进行三阶近似。
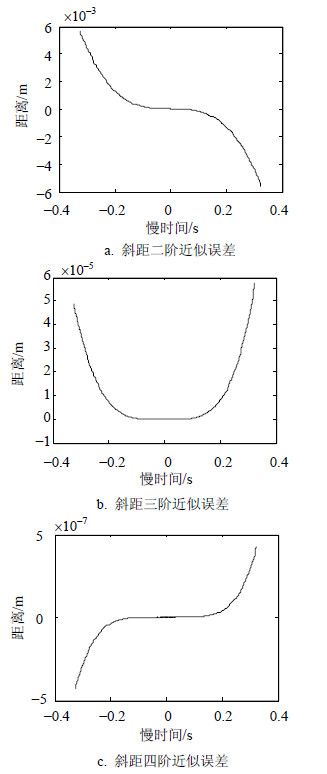 |
| 图3斜距误差分析 |
点目标仿真实验对文献[12]采用的斜距二阶近似成像方法与本文采用斜距四阶近似成像方法的成像结果进行对比验证。坐标分别为(10, 19.9) km,(10, 20) km,(10, 20.1) km的3个点A、B、C的成像结果如图 4所示。图 4a为采用斜距二阶近似方法3个点目标等高线图,图 4b为本文方法3个目标点的等高线图,图 4c为点目标的方位向剖面图对比。以点B为例,本文方法获得的点B方位向峰值旁瓣比(PSLR)和积分旁瓣比(ISLR)分别为-13.23 dB和-9.71 dB,文献[12]所采用的斜距二阶近似获得的PSLR和ISLR分别为-7.30 dB和-6.18 dB。可以看出,采用斜距二阶近似时,点目标聚焦效果较差,且方位像主瓣展宽和旁瓣电平升高,而采用斜距四阶近似所得的点目标成像结果,方位像的聚焦效果得到了较大的改善。表 1给出了本文方法的3个点成像质量评估结果,可见本文方法在方位向分辨率为0.3m的情况下仍能获得较好的成像结果。
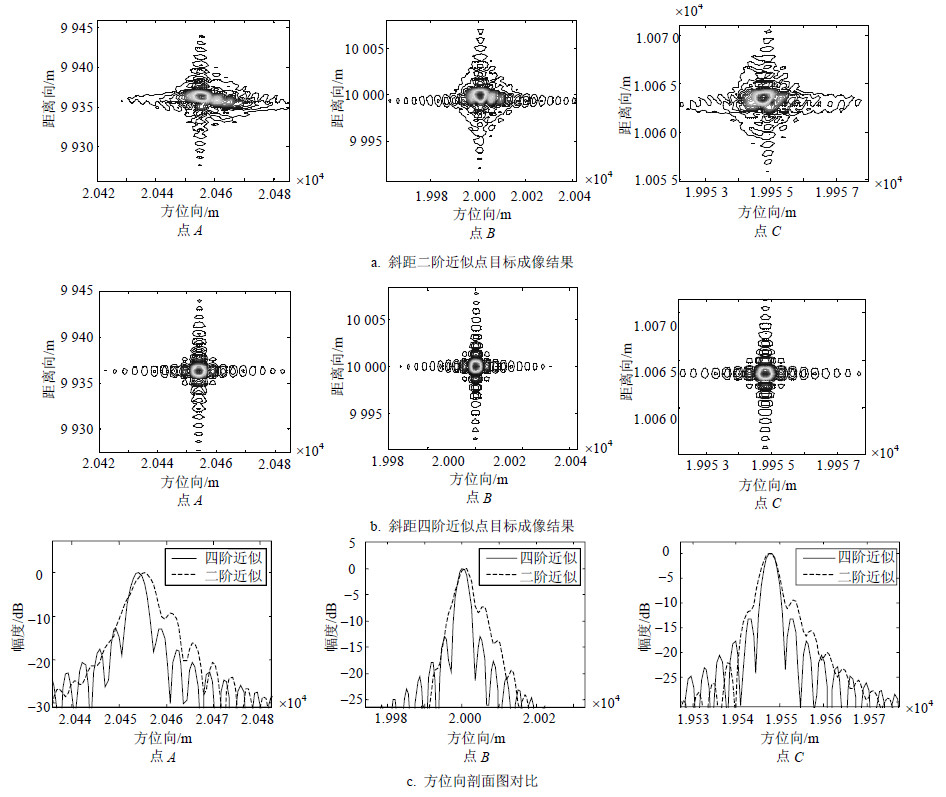 |
| 图4点目标成像结果对比 |
| 表1 成像质量 |
图 5为仿真场景目标成像结果对比,仿真参数与点目标仿真参数一致,仿真场景大小为256×256像素点。其中图 5a为采用斜距二阶近似场景目标成像结果,图 5b为采用本文方法场景目标成像结果。进一步分别对图 5中方框区域进行放大对比,对比结果如图 6所示。可以看出,本文方法与采用斜距二阶近似的成像方法相比能够更好地改善成像质量,目标的聚焦效果更好。
 |
| 图5局部放大成像结果对比 |
FMCW SAR由于其自身的优越性,必将在精确制导领域受到越来越广泛的关注。本文对弹载FMCW SAR俯冲成像方法展开研究,在建立斜距高阶近似的基础上,推导分析了回波差频信号精确方位多普勒频域表达式,并提出了相应的成像方法。该成像方法不涉及插值操作,且步骤简单,具有较高的运算效率,能够为FMCW SAR系统应用于精确制导领域提供一定的参考。
| [1] | 周鹏,熊涛,周松,等.一种新的弹载SAR高分辨成像方法[J].电子与信息学报, 2011, 33(3): 622-627. ZHOU Peng, XIONG Tao, ZHOU Song, et al. A novel high resolution imaging method for the missile-borne SAR[J]. Journal of Electronics and Information Technology, 2011, 33(3): 622-627. |
| [2] | META A, HOOGEBOOM P, LIGTHART L P. Signal processing for FMCW SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3519-3532. |
| [3] | LIU Y, DENG Y, WANG R, et al. Efficient and precise frequency-modulated continuous wave synthetic aperture radar raw signal simulation approach for extended scenes[J]. IET Radar Sonar Navig, 2012, 6(9): 858-866. |
| [4] | STOVE A G. Linear FMCW radar techniques[J]. IEE Proc Radar Sonar Navig, 1992, 139(5): 343-350. |
| [5] | ADVE R. Bistatic FMCW SAR signal model and imaging approach[J]. IEEE Transactions on Aerospace and Electronic Systems. 2013, 49(3): 2017-2028. |
| [6] | EDRICH M. Ultra-light weight synthetic aperture radar based on a 35GHz FMCW sensor concept and online raw data transmission[J]. IEE Proc Radar Sonar Navig, 2006, 153(2): 129-134. |
| [7] | WANG R, LUO Yun-hua, DENG Yun-kai, et al. Motion compensation for high-resolution automobile FMCW SAR[J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1157-1161. |
| [8] | 肖忠源,徐华平,李春升.基于俯冲模型的频域距离走动校正NLCS-SAR成像算法[J].电子与信息学报, 2013, 35(5): 1090-1096. XIAO Zhong-yuan, XU Hua-ping, LI Chun-sheng. NLCS-SAR imaging algorithm with range-walk correction in frequency domain based on dive model[J]. Journal of Electronics and Information Technology, 2013, 35(5): 1090-1096. |
| [9] | 梁毅,郭亮,邢孟道,等.一种斜视FMCW SAR的等效正侧视处理方法[J].电子学报, 2009, 37(6): 1159-1164. LIANG Yi, GUO Liang, XING Meng-dao, et al. An equivalent side-looking method for squint FMCW SAR[J]. Acta Electronica Sinica, 2009, 37(6): 1159-1164. |
| [10] | EVAN C Z, DAVID G L. Theory and application of motion compensation for LFM-CW SAR[J]. IEEE Transactionon Geoscience and Remote Sensing, 2009, 46(10): 2990-2998. |
| [11] | 张双喜,李军,张磊,等.基于级数反演的斜视FMCW SAR成像算法研究[J].电子学报, 2013, 41(3): 532-538. ZHANG Shuang-xi, LI Jun, ZHANG Lei, et al. Frequency modulated continuous wave squint synthetic aperture radar imaging algorithm based on series reversion[J]. Acta Electronica Sinica, 2013, 41(3): 532-538. |
| [12] | 周松,周鹏,张磊,等.调频连续波弹载SAR成像方法[J].系统工程与电子技术, 2011, 33(10): 2203-2209. ZHOU Song, ZHOU Peng, ZHANG Lei, et al. Imaging of missile-borne SAR based on FMCW[J]. Systems Engineering and Electronics, 2011, 33(10): 2203-2209. |
| [13] | 保铮,邢孟道,王彤.雷达成像技术[M].北京:电子工业出版社, 2005. BAO Zheng, XING Meng-dao, WANG Tong. Radar Imaging technique[M]. Beijing: Publishing House of Electronics Industry, 2005. |
| [14] | 周鹏,周松,熊涛,等.基于级数反演的弹载SAR下降段CZT成像算法[J].电子与信息学报, 2010, 32(12): 2861-2867. ZHOU Peng, ZHOU Song, XIONG Tao, et al. A chirp-Z transform imaging algorithm for missile-borne SAR with diving maneuver based on the method of series reversion[J]. Journal of Electronics and Information Technology, 2010, 32(12): 2861-2867. |
| [15] | 易予生,张林让,刘楠,等.基于级数反演的俯冲加速运动状态弹载SAR成像算法[J].系统工程与电子技术, 2009, 31(12): 2863-2866. YI Yu-sheng, ZHANG Lin-rang, LIU Nan, et al. Imaging algorithm for missile-borne SAR with diving acceleration based on series reversion[J]. Systems Engineering and Electronics, 2009, 31(12): 2863-2866. |
 2015, Vol. 44
2015, Vol. 44
