2. 电子科技大学生命科学与技术学院 成都 610054;
3. 西南交通大学生命科学与工程学院 成都 610031
2. School of Life Science and Technology, University of Electronic Science and Technology of China Chengdu 610054;
3. School of Life and Science Engineering, Southwest Jiaotong Univerity Chengdu 610031
儿童注意缺陷与多动症(attention deficit/ hyperactivity disorder, ADHD)是一种常见的神经性发育性障碍,通常表现为注意力不集中,多动或者二者联合的症状[1]。据统计学龄期的儿童发病率高达5%左右,ADHD的研究已成为世界的一个公共卫生问题[1, 2],引起了人们广泛的关注。目前,对ADHD的诊断和治疗都有较大的难度,缺乏客观的指标。模式识别的方法越来越广泛地应用于ADHD的研究中[3, 4],基于不同的功能磁共振数据特征参数被提取(如功能连接、低频振幅、不同模板下提取的脑区平均时间序列等)用于ADHD的分类。然而,基于这些特征的分类结果并不是很理想,2011年,在美国1000 Functional Connectomes Project项目组组织的全球范围的ADHD分类大赛(‘The ADHD200 Global Competition’)中,基于这些特征参数,21个参赛团队中最高的分类准确率只有61.3% (195个测试样本中119个分类正确)[4, 5]。
小波分析作为一种非常重要的信号时频分析手段,具有良好的局部化性质,可以聚焦到信号的任意细节水平,近年来在磁共振信号处理中的应用越来越广泛[6]。多种基于小波变换的特征提取的方法被用于构建分类特征参数,如求取小波系数平均值、绝对平局值、能量值等。其中小波系数能量值作为分类参数具有重要的意义[6, 7]。
功能磁共振成像(functional magnetic resonance imaging, fMRI)是一种无创的被广泛应用于测量大脑活动的工具。功能磁共振数据的信噪比低、数据量大,但是文献[8]认为传统的分类算法仍然可以对这些数据进行分类,特别是SVM (support vector machine)具有小样本学习和较好的泛化能力,在fMRI数据分类中得到了青睐。本文选取的功能磁共振数据来源于ADHD分类大赛,该数据量大,而且是多中心数据。50名ADHD儿童和65名健康儿童的静息态磁共振信号被用于研究。本文利用小波变换实现对信号的多尺度分解和构建小波系数能量值特征参数,并结合SVM分类器进行分类。最后找到能够有效区分ADHD病人与正常儿童的相关生物标记,为实际临床诊断提供有价值的参考。
1 实验数据及预处理 1.1 数据来源本文研究的静息态功能磁共振数据来自ADHD-200竞赛网北京中心数据集数据。总共有194名儿童,其中正常儿童114人,女孩46人,男孩68人。平均年龄11岁;ADHD儿童80人,女孩10人,男孩70人,平均年龄12岁,所有的儿童都没有精神分裂、情感障碍、精神发育迟滞、神经系统以及发育障碍疾病,且均无特殊家族遗传性疾病史。
1.2 数据预处理对所有静息态fMRI数据采用SPM8软件包进行预处理,主要包括时间校正、头动校正、空间标准化(3mm × 3mm × 3mm)以及8 mm高斯核平滑。其中头部平动大于2 mm并且转动大于2°和空间标准化匹配不完整的被试被排除,最终有50名ADHD儿童和65名正常儿童的静息态磁共振数据用于进一步的处理。
根据自动解剖标定(automated anatomical labeling, AAL) 模板,配准后的静息态功能MRI数据被分割为116个感兴趣区域(78个皮层区域、12个皮下区域和26个小脑区域)。对每一个被试考虑90脑区为感兴趣区域。首先提取90个脑区每个区域的平均时间序列。为了消除整理噪声的影响,本文对这些时间序列进行带通滤波(0.01~0.08 Hz),而且回归了6个头动参数、白质信号、脑脊液信号以及它们的一阶导数,这个过程主要是去除不太可能参与神经元特定区域相关性的变量[7, 8]。由于目前对于是否回归全脑平均信号存在较大的争议,本文没有进行全脑信号回归处理。
2 相关基本理论 2.1 小波变换 2.1.1 基本原理设函数$\psi \left( t \right) \in {L^2}\left( R \right)$满足容许条件:
| ${C_\psi } = \int_{ - \infty }^{ + \infty } {\frac{{{{\left| {\hat \psi (\omega )} \right|}^2}}}{{{{\left| \omega \right|}^{}}}}{\rm{d}}\omega < \infty } $ | (1) |
| ${\psi _{a,b}}(t) = {\left| a \right|^{1/2}}\psi \left( {\frac{{t - b}}{a}} \right){\rm{ }}b \in R,a \in R,a \ne 0$ | (2) |
假如时间序列信号为f(t),则f(t)的小波变换定义为:
| ${W_\psi }f(a,b) = {\left| a \right|^{1/2}}\int_R {(t)} \bar \psi \left( {\frac{{t - b}}{a}} \right){\rm{d}}t$ | (3) |
小波变换的本质就是利用这一组基函数对信号进行分解,从而实现对信号的时频分析。在实际数据处理中可供选择的小波基一般有Daubechies (dbN)系列、Symlet (symN)系列、Mexican小波以及Morlet小波等。这些小波都具有一定紧支撑性、对称性和平滑性的正交小波[11]。
2.1.2 BOLD一维信号的小波分解一维信号进行离散小波分解,分别得到信号的近似成份和细节成分,即高频部分和低频部分,而低频部分通常包含了信号的主要信息。实际信号处理中要对信号进行多尺度小波分解,该特性可以更精确的获得信号的深层信息。本文选择对血氧依赖水平(blood oxygenation level dependent, BOLD)信号进行3层分解,主要是因为磁共振信号的频率较低(0~0.25 Hz),并且为了降低分类特征维度。图 1给出了BOLD信号一维小波分解的具体流程[7]。A1、A2表示为信号小波分解的低频近似成份;D1、D2表示为信号小波分解的高频细节成份。
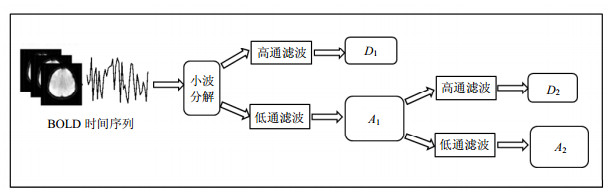 |
| 图1 小波分解示意图 |
小波函数具有多样性,在磁共振时间序列中,选择不同的小波基处理同一数据,可能会得到不同的结果,因此寻找某一BOLD时间序列处理的最优小波基十分必要。
本文介绍一种最优小波基选取方法,其判断的准则是根据Mallat算法对原始信号f1仅作单尺度小波分解与重构处理[11, 12],然后计算重构信号f2与原始信号f3之间的误差。误差计算公式为:
| $\left\| {{f_1} - {f_2}} \right\| = \sqrt {\sum\limits_{i = 1}^N {{{({f_{1i}} - {f_{2i}})}^2}} } $ |
下面以一个BOLD信号在不同小波基下分解与重构的误差进行分析为例,来说明最优小波基的选取。其中db和sym系列小波分解和重构之后的误差如表 1和表 2所示。
| 表1 db系列小波分解重构之后的误差 |
| 表2 sym系列小波分解重构之后的误差 |
通过表 1与表 2发现,db1小波基分解重构的误差最低,因此本文在处理BOLD信号中将选择db1作为小波基。图 2是选用db1小波对一个BOLD信号进行小波变换与重构的结果。由图 2可以看出,原始信号和重构信号只有微小的误差。
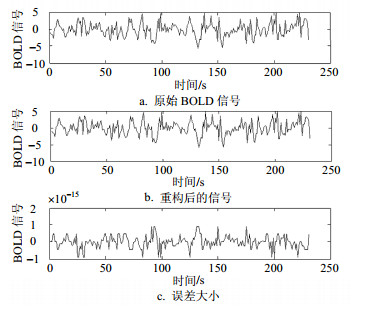 |
| 图2 db1小波分解与重构效果图 |
对于n个m维线性不可分样本有:
| $({x_1},{y_1}), \cdot \cdot \cdot ,({x_n},{y_n}) \in {R^m} \times \left\{ { - 1,1} \right\}$ | (4) |
在高维空间中构造的最优超平面满足:
| ${y_i}[\omega \cdot \phi ({x_i}) + b] \ge 1\begin{array}{*{20}{c}} {} \end{array}{\rm{ }}i = 1,2, \cdot \cdot \cdot ,n$ | (5) |
将该问题转化为二次规划问题:
| $\min J(\omega ,\xi ) = \frac{1}{2}{\left\| \omega \right\|^2} + C\sum\limits_{i = 1}^n {{\xi _i}} $ | (6) |
| $Q(a) = \sum\limits_{i = 1}^N {{a_i}} - \frac{1}{2}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{a_i}{a_j}{y_i}{y_j}K({x_i},{x_j})} } $ | (7) |
| $\sum\limits_{j = 1}^N {{a_i}{y_i} = 0{\rm{ }}{a_i}} \ge 0{\rm{ }}i = 1,2, \cdot \cdot \cdot ,N$ | (8) |
| $D(x) = {\mathop{\rm sgn}} (\sum\limits_{i = 1}^n {a_i^*} {y_i}(x{x_i}) + \omega _0^*)$ | (9) |
1) 线性核为$K({x_i},{x_j}) = < {x_i},{x_j} > $;
2) 多项式核为$K({x_i},{x_j}) = {( < {x_i},{x_j} > + c)^p}c \ge 0$, P是自然数;
3) 高斯核(径向基RBF)为$K({x_i},{x_j}) = $$\exp \left( {\frac{{ - {{\left\| {{x_i} - {x_j}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)\sigma > 0$;
4) Sigmoid核为$K({x_i},{x_j}) = \tanh (\gamma x_i^{\rm{T}}{x_j} + r)$。
3 ADHD病人静息态磁共振BOLD信号特征提取与分类方法 3.1 能量表征及特征参数提取信号经小波变换后可以得到很多的描述信号模式的特征,获取各种候选特征子集为进一步的分类做好准备。文献[4]介绍了以小波变换的结果进行特征表示的各种常用方法。其中能量作为特征的方法被广泛的应用。
设${E_{jk}} = {\left| {{D_j}(k)} \right|^2}$为信号$f(t)$在第$j$尺度$k$点的小波能量,那么${E_j} = \sum\limits_{k = 1}^N {{E_{jk}}} $就为第j尺度下$k = 1,2, \cdots ,N$个采样点的信号能量和,其中${D_j}(k)$为BOLD信号经小波变换后第j尺度下k各数据[13, 15]。
大量磁共振信号研究表明,人脑活动主要与固有的低频振荡(0.01~0.08 Hz)有关。本文中预处理的数据已经经过滤波处理,因此着重考虑经小波分解后各频率段信号能量作为分类特征对ADHD病人进行分类。根据文献[13, 14],基于小波变换的静息态BOLD信号特征提取的算法如下:
1) 利用AAL模板提取经过预处理后的90个脑区的平均时间序列信号;
2) 选用db1最优小波基对提取的平均时间序列信号进行3层小波分解,分别获得低频信号成份CA3和3个高频信号成份CD3,CD2,CD1;
3) 提取各尺度小波系数,计算小波系数能量值,构造用于分类的特征向量为:
| $T = [E(C{A_3}),E(C{D_3}),E(C{D_2}),E(C{D_1})]$ |
4) 对特征向量进行归一化,总的信号能量记做${E_0}$,则:${E_0} = E(C{A_3}) + E(C{D_3}) + E(C{D_2}) + E(C{D_1})$,因此归一化后的特征向量为:
| $\begin{array}{c} \bar T = [E(C{A_3})/{E_0},E(C{D_3})/{E_0},\\ E(C{D_2})/{E_0},E(C{D_1})/{E_0}] \end{array}$ |
5) 用SVM分类器对ADHD病人和正常人进行分类,并进行决策和获得分类权重显著高的脑区。
图 3给出了基于小波变换特征提取与SVM进行分类的算法框图。
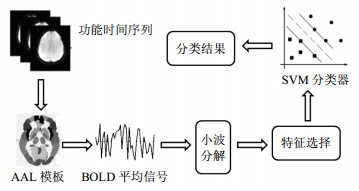 |
| 图3 BOLD时间序列经小波变换后进行特征提取和SVM分类的处理框图 |
本文采用了较大的样本量,用留一法来评估分类器的性能。利用准确率(accuracy, ACC)、敏感性(sensitivity, SEN)和特异性(specificity, SPE)这些指标来量化分类器的性能。各项指标计算方法如下[4, 10]:
| ${\rm{ACC = }}\frac{{{\rm{TP + TN}}}}{{{\rm{TP + TN + FP + FN}}}}$ |
| ${\rm{SEN = }}\frac{{{\rm{TP}}}}{{{\rm{TP + FN}}}}$ |
| ${\rm{SPE = }}\frac{{{\rm{TN}}}}{{{\rm{TN + FP}}}}$ |
| $P = \frac{{\sum\limits_{i = 1}^m {\left| {\left\{ {{\rm{ACC}}(\hat S) \ge ACC(S)} \right\} + 1} \right|} }}{{m + 1}}$ |
小波多尺度分解可以得到各个尺度频段上的信号特征,因此将不同尺度上信号的能量值作为分类的特征向量是可行的[12]。本文选择了SVM作为分类器,使用了LIBSVM工具包,惩罚参数c为默认值(c=1)。在评估分类器的性能方面,使用的是嵌入式留一法交叉验证,这种方法可以对真实的泛化能力进行相对无偏的估计[10]。最优SVM模型和最优特征子集由内部交叉验证获得,然后用于对测试集样本进行测试[10]。另外,核函数对分类器的分类效果也有显著的影响,本文分别讨论了线性核与高斯核对分类结果的影响,表 3给出了分类性能结果、AUC (p=0.025)值及方法比较,图 4给出了基于线性核对应的ROC曲线及曲线下面积。获得的平均准确率为62.7%,这个结果好于ADHD-200 全球竞赛中冠军队基于图像特征的61.3%的分类结果。因此,基于小波分解以信号的能量作为特征的方法是有效的。
| 表3 以信号能量作为特征的线性和非线性分类器性能比较 |
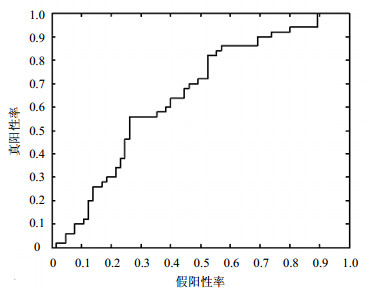 |
| 图4 基于信号能量作为特征的分类ROC曲线 |
不同的区域的信号特征在分类的过程中表现出不同的分类权重,基于权重的大小可以帮助我们初步推断那些脑区可能在疾病中扮演重要的角色。通常,如果一些脑区的权重大于所有区域权重的均值加上一倍的标准差,就把这些区域看作是有显著高的权重[16]。图 5显示了基于这个判别标准下13个脑区拥有显著高的分类权重,并给出了相应脑区的位置分布。左侧为脑区的标准化权重降序排列图,黑线表示为权重为均值加一倍标准差的分界线;右侧为权重显著高的脑区的位置分布,节点的大小代表了权重的大小。这些脑区主要是:左侧背外侧上回、左侧眶部额上回、左侧额中回、右侧眶部额中回、左侧岛盖部额下回、右侧眶部额下回、右侧中央沟盖、左右眶内额上回、左侧后扣带回、左侧距状裂周围皮层、右侧豆状壳核、右侧丘脑。
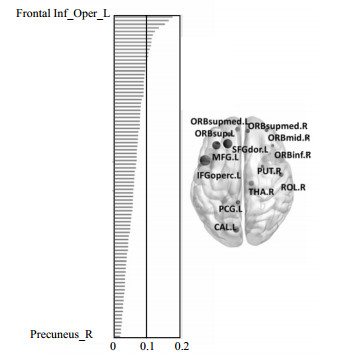 |
| 图5 基于SVM分类的90个脑区分类权重示意图 |
本文发现权重较高的脑区主要在额顶区域,表明ADHD病人相对于正常人来说额顶区域的BOLD信号能量存在异常,与之前的研究结论相一致[17, 18]。
5 结束语本文提取了大尺度功能时间序列平均信号,通过小波多尺度分解获取了大脑信号的深层信息特性。通过计算信号的内在小波系数能量值来构造了分类特征向量,并利用SVM分类器来进行分类。该分类器的分类准确率虽然只有62.7%,但是优于ADHD-200全球竞赛第一名的分类结果[4],且从信号能量分布的角度,这有助于对ADHD病人的影像学诊断及其机制的理解。本文发现13个脑区有显著的分类权重,这些脑区的BOLD信号能量的差异可能成为区分ADHD病人与健康人的重要的生物标记。另外也发现小波变换在对功能磁共振信号分解与特征提取上是一种有效的方法,以后将进一步探讨如何提高小波变换在功能影像学分类中的准确率。
| [1] | POLANCZK G, DE LIMA M S, HORTA B L, et al. The worldwide prevalence of ADHD: a systematic review and metaregression analysis[J]. Am J Psychiatry, 2007, 164(6): 942-948. |
| [2] | SELLERS R, MAUGHAN B, PICKLES A, et al. Trends in parent and teacher rated emotional, conduct and ADHD problems and their impact in prepubertal children in Great Britain: 1999-2008[J]. Journal of Child Psychology and Psychiatry, 2015, 56(1): 49-57. |
| [3] | ANURADHA J, RAMACHANDRAN V, ARULALAN K V, et al. Diagnosis of ADHD using SVM algorithm[C]// Proceedings of the Third Annual ACM Bangalore Conference. [S.l.]: ACM, 2010. |
| [4] | GUO X, AN X, KUANG D, et al. ADHD-200 Classification based on social network Method[C]//Intelligent Computing in Bioinformatics. Taiyuan, China: Springer International Publishing, 2014: 233-240. |
| [5] | 李长斌. 基于脑活动网络特征的ADHD分类研究[D]. 北 京: 北京交通大学, 2014. LI Chang-bin. Research on classification of ADHD based on the characteristic in brain activity-network[D]. Beijing: Beijing Jiaotong University, 2014. |
| [6] | AMIN H U, MALIK A S, AHMAD R F, et al. Feature extraction and classification for EEG signals using wavelet transform and machine learning techniques[J]. Australasian Physical & Engineering Sciences in Medicine, 2015, 38(1): 139-149. |
| [7] | 张晓文, 杨熠普, 许晓鸣. 基于小波变换的特征构造与选 择[J]. 计算机工程与应用, 2003, 19(19): 25-28. ZHANG Xiao-wen, YANG Yu-pu, XU Xiao-ming. Wavelet based feature representation[J]. Computer Engineering and Applications, 2003, 19(19): 25-28. |
| [8] | MITCHELL T M. Learning to decode cognitive states from brain images[J]. Machine Learning, 2004, 57(1-2): 145-175. |
| [9] | WEI Liao. Altered functional connectivity and small-world in mesial temporal lobe epilepsy[J]. PLoS One, 2010, 5(1): e8525. |
| [10] | 刘风. 基于磁共振成像的多变量模式分析方法学研究[D]. 成都: 电子科技大学, 2014. LIU Feng. MRI-based multivariate pattern analysis methodologies and applications[D]. Chengdu: University of Electronic Science and Technology of China, 2014. |
| [11] | 孙延奎. 小波分析及其应用[M]. 北京: 机械工业出版社, 2005. SUN Yan-kui. Wavelet analysis and its application[M]. Beijing: China Machine Press, 2005. |
| [12] | 成谢锋, 杨贺. 5种小波在心音信号处理中的分析与比较[J]. 南京邮电大学学报, 2015, 35(2): 39-46. CHENG Xie-feng, YANG He. Analysis and comparison of five kinds of wavelet in processing heart sound signal[J]. Journal of Nanjing University of Posts and Telecommunications, 2015, 35(2): 39-46. |
| [13] | JIAG Y E,LIN Y P. Error Estimation of INS ground alignment through observability analysis[J]. IEEE Transactions on Aerospace and Electronic Sstems, 1992, 28(1): 92-97. |
| [14] | 肖汉光, 蔡从中. 特征向量的归一化比较性研究[J]. 计 算机工程与应用, 2009, 45(22): 117-119. XIAO Han-guang, CAI Cong-zhong. Comparison study of normalization of feature vector[J]. Computer Engineering and Applications, 2009, 45(22): 117-119. |
| [15] | 张丽琼, 王炳和. 基于小波变换的脉象信号特征提取方 法[J]. 数据采集与处理, 2004, 19(3): 322-325. ZHANG Li-qiong, WANG Bin-he. Feature extraction methods for pulse signal based on wavelet transform[J]. Journal of Data Acquisition & Processing, 2004,19(3): 322-325. |
| [16] | TIAN L, WANG J. Hemisphere and gender-related differences in small-world brain networks: a resting-state functional MRI study[J]. NeuroImage, 2011, 54(1): 191-202. |
| [17] | VAIDYA C J, BUNGE S A, DUDUKOVIC N M, et al. Altered neural substrates of cognitive control in childhood ADHD: Evidence from functional magnetic resonance imaging[J]. Am J Psychiatry, 2005, 162(9): 1605-1613. |
| [18] | SOLANTO M V, MARKS D J, WASSERSTEIN J, et al. Efficacy of meta-cognitive therapy for adult ADHD[J]. The American Journal of Psychiatry, 2010, 167(8): 958-968. |
 2015, Vol. 44
2015, Vol. 44
