2. 盲信号处理国家重点实验室 成都 610041
2. National Key Laboratory on Blind Signals Processing Chengdu 610041
随着正交频分复用(OFDM)技术和频率复用技术的广泛应用,多载波信号同频干扰问题已成为一个不可忽视的问题。无论是第三代和第四代地面移动通信系统中邻近小区造成的同频干扰,还是卫星通信系统(如IPSTAR)中相邻卫星产生的同频干扰,都会严重影响通信系统的性能。为了解决该问题,需要实现多载波混叠信号分离,在这之前先要估计各路信号的调制参数及信道响应[1, 2, 3, 4, 5]。
目前,关于OFDM符号速率估计算法的研究是针对单个OFDM信号,如基于循环谱的方法[6]、基于循环自相关的方法[7]、基于小波变换方法[8]等;而混叠信号符号速率估计算法的研究主要是围绕单载波混叠信号展开的,如文献[9]中通过倍频实现BPSK、QPSK等单载波混叠信号符号速率估计;文献[10]利用四阶循环累积量的功率谱实现了双信号的码元速率估计,适合信号集为BPSK、QPSK和16QAM;文献[11, 12]通过循环谱实现BPSK、QPSK、8QAM混叠信号符号速率估计。
上述方法都不能直接应用于OFDM混叠信号,为此本文针对该问题展开研究,分析单个OFDM信号和两个OFDM混叠信号循环谱特性,比较两者之间存在的差异,并在此基础上提出了一种单通道OFDM混叠信号符号速率估计算法,它不仅可以同时估计两个OFDM信号的符号速率,且还具备检测接收信号是否为OFDM混叠信号的能力,为信号的后续处理提供支撑。
1 信号模型考虑单信道混合信号接收系统,接收机同时接收到两个OFDM信号,其接收信号模型可以写成:
| $ x(t) = {x_1}(t) + {x_2}(t) + n(t) $ | (1) |
| $ {x_i}(t) = {\mathop{\rm Re}\nolimits} \left\{ {{h_i}{{\rm{e}}^{{\rm{j}}(2{\rm{\pi }}{f_i}t + {\phi _i})}}\left\{ {\frac{1}{{{N_i}}}\sum\limits_{n = - \infty }^\infty {\sum\limits_{k = 0}^{{M_i} - 1} {\sum\limits_{m = 0}^{{N_i} - 1} {a_{_{m,n}}^i\exp ({\rm{j}}2{\rm{\pi }}m(k - {L_i})/{N_i})g(t - k{T_i} - n{M_i}T_s^i - t_0^i)} } } {\kern 1pt} } \right\}} \right\}{\kern 1pt} $ | (2) |
| $ {x_i}(t) = {\mathop{\rm Re}\nolimits} \left\{ {{h_i}{{\rm{e}}^{{\rm{j}}(2\pi {f_0}t + {\phi _i})}}\left\{ {\frac{1}{N}\sum\limits_{n{\rm{ = }} - \infty }^\infty {\sum\limits_{k{\rm{ = }}0}^{N - 1} {\sum\limits_{m{\rm{ = }}0}^{N - 1} {a_{_{m{\rm{,}}n}}^i\exp ({\rm{j}}2{\rm{\pi }}mk{\rm{/}}N{\rm{)}}g(t - k{T_i} - nNT_s^i - {t_i})} } } {\kern 1pt} } \right\}} \right\} $ | (3) |
本文研究基于该信号模型在没有任何先验信息的条件下对两路OFDM分量信号的符号速率(Ti)进行盲估计。下面分析混合前后信号循环谱特性的变化,探讨符号速率的盲估计方法。
2 符号速率估计方法 2.1 混叠信号的循环平稳特性根据信号及噪声的独立性,可以得到接收信号$x(t)$的均值${m_x}$为:
| $ {m_x} = {m_{{x_1}}} + {m_{{x_2}}} + {m_n}{\rm{ = }}0 $ | (4) |
接收信号$x(n)$的时变自相关函数定义为${m_{2x}}{\rm{(}}\tau {\rm{)}} = E\{ x(t){x^*}(t + \tau )\} $,其中上标“*”表示共轭运算,有:
| $ {m_{2x}}{\rm{(}}\tau {\rm{)}} = {m_{2{x_1}}}{\rm{(}}\tau {\rm{)}} + {m_{2{x_2}}}{\rm{(}}\tau {\rm{)}} + {m_{2n}}{\rm{(}}\tau {\rm{)}} $ | (5) |
又${m_{2n}}{\rm{ = }}0$,且由文献[6]知单个OFDM信号自相关函数为周期为Ti的周期函数,根据式(5)可知m2x为周期函数,其周期为Ti的最小公倍数Ts。根据循环平稳特性可知$x(t)$为循环平稳信号[7]。
结合循环谱密度函数定义和前面推导可知:
| $ \begin{array}{l} m_{2x}^\alpha (\tau ) = \frac{1}{{{T_s}}}\int_{{\rm{ - }}{T_s}{\rm{/}}2}^{{T_s}{\rm{/}}2} {{m_{2{x_1}}}(\tau )} {\rm{exp}}( - {\rm{j}}2{\rm{\pi }}\alpha t){\rm{d}}t{\rm{ + }}\\ \;\;\;\;\;\;\;\;\frac{1}{{{T_s}}}\int_{{\rm{ - }}{T_s}{\rm{/}}2}^{{T_s}{\rm{/}}2} {{m_{2{x_2}}}} {\rm{exp}}( - {\rm{j}}2{\rm{\pi }}\alpha t){\rm{d}}t \end{array} $ | (6) |
| $ m_{{x_i}}^{{\alpha _i}}(\tau ) = \frac{1}{{T_s^i}}\int_{{\rm{ - }}T_s^i{\rm{/}}2}^{T_s^i{\rm{/}}2} {{m_{2{x_i}}}} {\rm{exp}}( - {\rm{j}}2{\rm{\pi }}{\alpha _i}t){\rm{d}}t $ | (7) |
| $ \frac{1}{{{T_i}}}\int_{{\rm{ - }}{T_i}{\rm{/}}2}^{{T_i}{\rm{/}}2} {{m_{2{x_i}}}} {\rm{exp}}( - {\rm{j}}2{\rm{\pi }}{\alpha _i}t){\rm{d}}t{\rm{ = }}\frac{1}{{{T_s}}}\int_{{\rm{ - }}{T_s}{\rm{/}}2}^{{T_s}{\rm{/}}2} {{m_{2{x_i}}}} {\rm{exp}}( - {\rm{j}}2{\rm{\pi }}\alpha t){\rm{d}}t $ | (8) |
| $ m_x^\alpha {\rm{(}}\tau {\rm{) = }}m_{{x_1}}^{{\alpha _{\rm{1}}}}{\rm{(}}\tau {\rm{) + }}m_{{x_2}}^{{\alpha _{\rm{2}}}}{\rm{(}}\tau {\rm{)}} $ | (9) |
通过式(9)可推导出:
| $ S_x^\alpha (f){\rm{ = }}S_{{x_1}}^\alpha (f) + S_{{x_2}}^\alpha (f{\rm{) = }}S_{{x_1}}^{{\alpha _{\rm{1}}}}{\rm{(}}f{\rm{)}} + S_{{x_2}}^{{\alpha _{\rm{2}}}}{\rm{(}}f{\rm{)}} $ | (10) |
综上所述,混叠OFDM信号是一个循环平稳信号,其循环谱密度函数等于各个OFDM信号循环谱密度函数之和。
2.2 单个OFDM信号与混叠OFDM信号循环谱特性差异分析1) 单个OFDM信号循环谱特性。
由式(3)可得到单个OFDM信号的表示为:
| $ {x_i}(t){\rm{ = }}\frac{1}{2}{h_i}\left\{ {{r_i}{\rm{(}}t{\rm{)}}{{\rm{e}}^{{\rm{j}}(2{\rm{\pi }}{f_i}t + {\phi _i})}}{\rm{ + }}r_i^{\rm{*}}{\rm{(}}t{\rm{)}}{{\rm{e}}^{ - {\rm{j}}(2{\rm{\pi }}{f_i}t + {\phi _i})}}} \right\} $ | (11) |
| $ \begin{array}{*{20}{c}} {{r_i}{\rm{(}}t{\rm{) = }}}\\ {\frac{1}{N}\sum\limits_{n{\rm{ = - }}\infty }^\infty {\sum\limits_{k{\rm{ = }}0}^{N - 1} {\sum\limits_{m{\rm{ = }}0}^{N - 1} {a_{_{m{\rm{,}}n}}^i\exp {\rm{(j}}2{\rm{\pi }}mk{\rm{/}}N{\rm{)}}g(t - k{T_i} - nN{T_i} - t_{\rm{0}}^i)} } } } \end{array} $ | (12) |
由循环谱性质$(S_{xx}^\alpha ( - f){\rm{ = }}S_{xx}^\alpha {\rm{(}}f{\rm{),}}S_{xx}^{ - \alpha }(f){\rm{ = }}S_{xx}^\alpha {(f{\rm{)}}^{\rm{*}}})$和循环谱的定义[10]可推导出当${\alpha _i}{\rm{ = }}k{\rm{/}}T_s^i$时,${x_i}(t)$的循环谱密度函数为:
| $ S_{{x_i}}^{{\alpha _i}}(f{\rm{)}} = \frac{1}{4}\{ S_{{r_i}{r_i}}^{{\alpha _i}}(f - {f_i}){\rm{ + }}S_{{r_i}{r_i}}^{{\alpha _i}}(f{\rm{ + }}{f_i})\} $ | (13) |
| $ \begin{array}{*{20}{c}} {S_{{r_i}{r_i}}^{{\alpha _i}}{\rm{(}}f{\rm{)}} = }\\ {\frac{1}{{T_s^i}}{{\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}{\alpha _i}t_0^i}}\left\{ {\sum\limits_{m{\rm{ = }}0}^{N - 1} {{{\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}m\Delta ft_0^i}}G{\rm{(}}f - m\Delta {f_i}{\rm{ + }}{\alpha _i}{\rm{)}}{G^{\rm{*}}}{\rm{(}}f - m\Delta {f_i}{\rm{)}}} } \right\}} \end{array} $ | (14) |
| $ G(f{\rm{) = }}A\sin {\rm{(\pi }}fT_s^i{\rm{)/(\pi }}f{\rm{)}} $ | (15) |
当${\alpha _i} \ne k{\rm{/}}T_s^i$时,$S_{{x_i}}^{{\alpha _i}}{\rm{(}}f{\rm{) = 0}}$。
从式(14)和式(15)可知,$S_{{x_i}}^{{\alpha _i}}{\rm{(}}f{\rm{)}}$在f截面(即$S_{{x_i}}^{{\alpha _i}}{\rm{(}}{f_o}{\rm{)}}$,${f_o}$为任意值)是以等间隔$1{\rm{/}}{T_i}$切片,即$S_{{x_i}}^{{\alpha _i}}{\rm{(}}{f_o}{\rm{)}}$仅仅在${\alpha _i}{\rm{ = }}k{\rm{/}}{T_i}$(k为整数)时取值不为零。
下面讨论$S_{{x_i}}^{{\alpha _i}}{\rm{(}}f{\rm{)}}$在$f{\rm{ = }} - {f_i}$截面模的特性(文献[13]给出了基于循环谱的${f_i}$估计方法)。由式(15)可知$G{\rm{(}}f{\rm{)}}$的值随着f的增加急剧减小,因此$\left| {S_{{x_i}}^{{\alpha _i}}{\rm{(}} - {f_i}{\rm{)}}} \right|$可简化为:
| $ \left| {S_{{x_i}}^{{\alpha _i}}( - {f_i}{\rm{)}}} \right| \approx \left| {\frac{{h_i^2}}{{4T_s^i}}\left\{ {\sum\limits_{m{\rm{ = }}0}^{N - 1} {{{\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}m\Delta {f_i}{t_i}}}G(m\Delta {f_i} - {\alpha _i}){G^{\rm{*}}}{\rm{(}}m\Delta {f_i}{\rm{)}}} } \right\}} \right| $ | (16) |
回顾前面的讨论,可得:
| $ \frac{{{{{\rm{(}}ANT_s^i{\rm{)}}}^2}\sin {\rm{(\pi (}}m{\rm{/}}N - k{\rm{))}}}}{{{\rm{(\pi (}}m - kN{\rm{))}}\sin {\rm{(\pi (}}m{\rm{/}}N{\rm{)/(\pi }}m{\rm{)}}}}{\rm{ }} $ | (17) |
将式(17)代入式(16),可得:
| $ \begin{array}{*{20}{c}} {\left| {S_{{x_i}}^{{\alpha _i}}( - {f_i})} \right| \approx }\\ {\left| {\frac{{h_i^2}}{{4{T_i}}}{{{\rm{(}}AN{T_i}{\rm{)}}}^2}\left\{ {\sum\limits_{m{\rm{ = }}0}^{N - 1} {{{\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}m\Delta {f_i}{t_i}}}{{\sin }^2}{\rm{(\pi (}}m{\rm{/}}N{\rm{)/(}}{{\rm{\pi }}^2}m{\rm{(}}m - kN{\rm{))}}} } \right\}} \right|} \end{array} $ | (18) |
从式(18)可知,当$\left| k \right| \ge 1$时,$\left| {S_{{x_i}}^{{\alpha _i}}( - {f_i})} \right|$随着$\left| k \right|$的增加而减小,即$\left| {S_{{x_i}}^{{\alpha _i}}( - {f_i})} \right|$随着$\left| {{\alpha _i}} \right|$的增加而减小;当k=0时,$\left| {S_{{x_i}}^{{\alpha _i}}( - {f_i})} \right|$取得最大值。
综上所述,单个OFDM信号循环谱密度函数在$f{\rm{ = }} - {f_i}$截面以$1{\rm{/}}{T_i}$等间隔切片,其模在k=0时取得最大值,且随着$\left| k \right|$的增加该模值逐渐减小。
2) 混叠OFDM信号循环谱特性。
为了讨论方便,本文假设混叠信号载频${f_1}{\rm{ = }}{f_2}{\rm{ = }}{f_c}$,此时接收信号$x(t)$的循环谱密度函数在$f{\rm{ = }} - {f_c}$截面的模可表示为:
| $S_x^\alpha ( - {f_c}{\rm{)}} = S_{{x_1}}^\alpha ( - {f_c}{\rm{)}} + S_{{x_2}}^\alpha ( - {f_c}{\rm{)}} $ | (19) |
假设${M_1}{T_1}{\rm{ = }}{M_2}{T_2}{\rm{ = }}{T_s}$(不失一般性,假设${M_1}{\rm{ < }}{M_2}$)。当${\alpha _{\rm{0}}}{\rm{ = }}r{\rm{/}}{T_s}$,$r \in Z$时,存在以下4种情况:
① 如果任意${m_1}$、${m_{\rm{2}}} \in Z$,都不满足${m_1}{\rm{/}}{T_1}{\rm{ = }}r{\rm{/}}{T_s}$,${m_2}{\rm{/}}{T_2}{\rm{ = }}r{\rm{/}}{T_s}$,此时$S_{{x_1}}^{{\alpha _0}}( - {f_c}){\rm{ = 0}}$,$S_{{x_2}}^{{\alpha _0}}( - {f_c}){\rm{ = 0}}$;
② 当存在${m_{\rm{1}}} \in Z$满足${m_1}{\rm{/}}{T_1}{\rm{ = }}r{\rm{/}}{T_s}$,且对任意${m_{\rm{2}}} \in Z$都有${m_2}{\rm{/}}{T_2} \ne r{\rm{/}}{T_s}$时,$S_{{x_1}}^{{\alpha _0}}( - {f_c}){\rm{ = }}S_{{x_1}}^{{m_1}{\rm{/}}{T_1}}( - {f_c})$,$S_{{x_2}}^{{\alpha _0}}( - {f_c}){\rm{ = 0}}$,${m_1}{\rm{ = }}r{\rm{/}}{M_1}$;
③ 当存在${m_{\rm{2}}} \in Z$满足${m_2}{\rm{/}}{T_2}{\rm{ = }}r{\rm{/}}{T_s}$,且对任意${m_{\rm{1}}} \in Z$都存在${m_1}{\rm{/}}{T_1} \ne r{\rm{/}}{T_s}$时,$S_{{x_1}}^{{\alpha _0}}( - {f_c}){\rm{ = }}S_{{x_1}}^{{m_1}{\rm{/}}{T_1}}( - {f_c})$,$S_{{x_1}}^{{\alpha _0}}( - {f_c}{\rm{) = 0}}$,${m_2}{\rm{ = }}r{\rm{/}}{M_2}$;
④ 当存在${m_1}、{m_{\rm{2}}} \in Z$同时满足${m_1}{\rm{/}}{T_1}{\rm{ = }}r{\rm{/}}{T_s}$,${m_2}{\rm{/}}{T_2}{\rm{ = }}r{\rm{/}}{T_s}$,$S_{{x_1}}^{{\alpha _0}}( - {f_c}){\rm{ = }}S_{{x_1}}^{{m_1}{\rm{/}}{T_1}}( - {f_c})$,$S_{{x_2}}^{{\alpha _0}}( - {f_c}){\rm{ = }}S_{{x_2}}^{{m_2}{\rm{/}}{T_2}}( - {f_c}{\rm{)}}$ ${m_1}{\rm{ = }}r{\rm{/}}{M_1}$,${m_2}{\rm{ = }}r{\rm{/}}{M_2}$。
该结果与式(10)中结果一致。此时,可分为以下两种情况:
Ⅰ. $\bmod {\rm{(}}{M_2}{\rm{/}}{M_1}{\rm{)}} \ne 0$(mod表示取余数)。
此时,$S_x^\alpha ( - {f_c})$包含以上4种情况,此时$S_x^\alpha {\rm{(}}f{\rm{)}}$在$f{\rm{ = }} - {f_c}$截面上脉冲分别在${m_1}{\rm{/}}{T_1}$和${m_2}{\rm{/}}{T_2}$位置处交替出现。与单个OFDM信号相比,混叠信号$S_x^\alpha ( - {f_c})$不再是等间隔切片。
Ⅱ. $\bmod {\rm{(}}{M_{\rm{2}}}{\rm{/}}{M_{\rm{1}}}{\rm{) = }}0$,即${T_1}{\rm{ = }}L{T_2}$,L为整数。
此时,$S_x^\alpha {\rm{(}} - {f_c}{\rm{)}}$只包含上述①、②、④3种情况。情况④中${m_1}{\rm{ = }}L{m_{\rm{2}}}$,${m_{\rm{2}}}{\rm{ = }}1,2, \cdots $,满足前面的讨论,可将情况④中$S_x^{{\alpha _0}}( - {f_c})$进一步简化为:
| $ S_x^{{\alpha _0}}( - {f_0}{\rm{)}} \approx \frac{{{{{\rm{(}}AN{\rm{)}}}^2}{T_1}}}{{4{m_1}}}{\rm{[}}{( - {\rm{1)}}^{{m_1}}}h_1^2{\rm{ + }}{( - {\rm{1)}}^{{m_2}}}h_2^2{\rm{]}} $ | (20) |
当m1和m2同为偶数或同为奇数时,可知:
| $ \left| {S_x^{r{\rm{/}}{T_s}}( - {f_c}{\rm{)}}} \right| \approx \frac{{{{{\rm{(}}AN{\rm{)}}}^2}{T_2}}}{{4{m_2}}}{\rm{[}}h_1^2{\rm{ + }}h_2^2{\rm{]}} $ | (21) |
| $ \left| {S_x^{{\rm{(}}r - 1{\rm{)/}}{T_s}}( - {f_c}{\rm{)}}} \right| \approx \frac{{{{(AN)}^2}L{T_2}}}{{4(L{m_2} - 1)}}h_1^2 $ | (22) |
由式(20)和式(22)容易得到:当$h_1^2{\rm{ < }}h_2^2{\rm{(}}L{m_2} - 1{\rm{)}}$时,$\left| {S_x^{r{\rm{/}}{T_s}}( - {f_c}{\rm{)}}} \right|{\rm{ > }}S_x^{{\rm{(}}r - 1{\rm{)/}}{T_s}}( - {f_c})$。
同理可知,当m1和m2一个为偶数,另一个为奇数时,且$h_1^2{\rm{ < }}h_2^2{\rm{(}}L{m_2} + 1{\rm{)}}$时,$\left| {S_x^{r{\rm{/}}{T_s}}( - {f_c}{\rm{)}}} \right|{\rm{ < }}S_x^{{\rm{(}}r{\rm{ + }}1{\rm{)/}}{T_s}}( - {f_c}{\rm{)}}$。
又${m_{\rm{2}}} \ge 1$,因此只要满足以下要求,混叠信号循环谱$\left| {S_x^\alpha ( - {f_c}{\rm{)}}} \right|$的递减特性将被改变,有:
| $ h_1^2{\rm{/}}h_2^2{\rm{ < }}L - 1 $ | (23) |
当满足式(23),接收方可通过能量跳变识别混叠信号,并提取各个信号的符号速率信息。式(23)中所示的条件是充分条件,非必要条件,实际中对L-1。
综上所述,当混叠OFDM信号符号速率不满足整数倍关系时,其循环谱在$f{\rm{ = }} - {f_0}$截面切片间隔不再满足等间隔特性;当混叠OFDM信号符号速率满足整数倍关系时,并且混叠信号的衰减幅度与L(符号速率之间的倍数)满足式(23),其循环谱在$f{\rm{ = }} - {f_0}$截面不再满足递减特性,切片幅度将出现跳变。接收方可以通过检测信号循环谱在$f{\rm{ = }} - {f_0}$截面切片是否慢等间隔特性和递减特性来判定该信号是否是混叠信号,并提出对应的符号速率。
3 实验仿真本文在高斯白噪声环境下对上述方法性能进行验证,仿真过程中采用Wimax协议产生OFDM信号。两个OFDM信号混叠,其载频${f_c}{\rm{ = 10 MHz}}$,子载波数为256,循环前缀长度为16,循环谱用FAM方法计算。
1) $\bmod {\rm{(}}{M_2}{\rm{/}}{M_1}{\rm{) = }}0$,即混叠OFDM信号符号速率满足整数倍关系。
仿真条件:信号S1的符号速率为1 Mb/s,信号S2的符号速率为4 Mb/s,信号幅度比$h_1^2{\rm{/}}h_2^2{\rm{ = }}1$。
信噪比为10 dB时,单信号谱密度函数$f{\rm{ = }} - {f_c}$截面特性如图 1所示。
 |
| 图1 信号S1、S2循环谱$f{\rm{ = }} - {f_c}$截面 |
图 1中信号S1和S2脉冲分别出现在$\alpha {\rm{ = 4}} \times {\rm{1}}{{\rm{0}}^6}r$和$\alpha {\rm{ = 1}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}r$处,脉冲幅度在$\alpha {\rm{ = }}0$两侧依次递减。该结果验证了OFDM单信号循环谱在$f{\rm{ = }} - {f_c}$截面的等间隔切片和随着$\left| k \right|$的增加一次递减的特性。此时混叠信号的循环谱在$f{\rm{ = }} - {f_c}$截面特性如图 2所示。
 |
| 图2 混叠信号循环谱$f{\rm{ = }} - {f_c}$截面 |
图 2在$\alpha {\rm{ = 4}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}r$出现能量跳变,该结果显示由于干扰OFDM信号的存在,改变了单个OFDM信号循环谱在$f{\rm{ = }} - {f_c}$截面脉冲幅度递减特性,验证了上一节$\bmod {\rm{(}}{M_2}{\rm{/}}{M_1}{\rm{)}} \ne 0$且满足幅度必要求条件下的分析结果。
该仿真条件下OFDM信号符号速率估计性能曲线如图 3所示。图 3显示了单信号和混叠信号的估计误差,单信号通过循环谱估计符号速率的精度高于10-6;信噪比低于3 dB时,混叠信号的估计性能急剧下降,无法完整提取到两个信号的符号速率信息,这是由于混叠信号之间的相互影响造成的。当信噪比高于3 dB时,估计性能较好(精度高于10-6)。
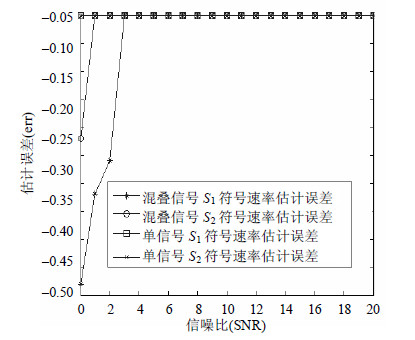 |
| 图3 符号速率估计误差 |
2) $\bmod {\rm{(}}{M_2}{\rm{/}}{M_1}{\rm{)}} \ne 0$,即混叠OFDM信号符号速率不满足整数倍关系。
仿真条件:信号S1的符号速率为$2.56{\rm{ Mb/s}}$,信号S2的符号速率为$4{\rm{ Mb/s}}$,信号幅度比$h_1^2{\rm{/}}h_2^2{\rm{ = }}1$。
信噪比为10 dB时,单信号谱密度函数$f{\rm{ = }} - {f_c}$截面特性如图 4所示。
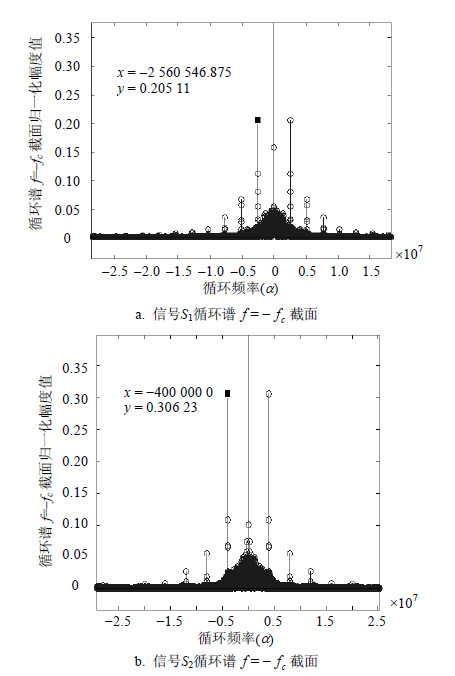 |
| 图4 信号S1、S2循环谱$f{\rm{ = }} - {f_c}$截面 |
图 4同样验证了OFDM单信号的等间隔和递减特性。此时混叠信号的循环谱在$f{\rm{ = }} - {f_c}$截面特性如图 5所示。
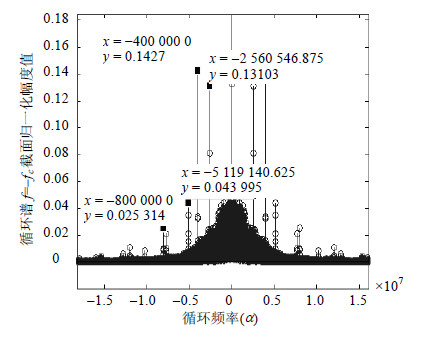 |
| 图5 混叠信号循环谱$f{\rm{ = }} - {f_c}$截面 |
从图 5可知此时混叠信号的脉冲在$\alpha {\rm{ = 4}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}r$和$\alpha \approx {\rm{2}}{\rm{.56}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}r$处交替出现,脉冲间间隔不再是等间距,即当$\bmod {\rm{(}}{M_2}{\rm{/}}{M_1}{\rm{)}} \ne 0$,混叠信号在$f{\rm{ = }} - {f_c}$截面等间隔切片特性再存在,同样与上一节分析结果一致。
该仿真条件下OFDM信号符号速率估计性能曲线如图 6所示。
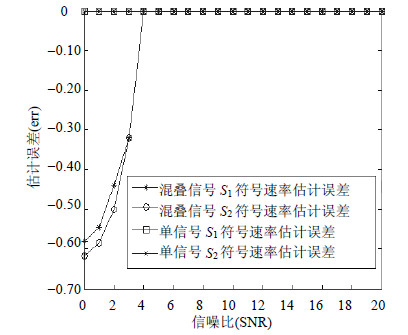 |
| 图6 符号速率估计误差 |
图 6显示在信噪比低于5 dB时混叠信号符号速率估计误差很大,从仿真结果知此时循环谱并未包含任何信号的符号速率信息,混叠条件其估计性能比1)中结果差,这是由于此时循环谱中切片间隔变小,相互影响增大导致的,当信噪比大于5 dB时,符号速率的估精度高(大于10-6)。
3) $h_1^2{\rm{/}}h_2^2$对符号速率估计性能的影响。
仿真条件:信号S1的符号速率为$1{\rm{ Mb/s}}$,信号S2的符号速率为$4{\rm{ Mb/s}}$,${\rm{SNR = }}15{\rm{ dB}}$,此时$L{\rm{ = }}4$。
当$h_1^2{\rm{/}}h_2^2$=5,混叠信号的循环谱在$f{\rm{ = }} - {f_c}$截面特性如图 7所示。
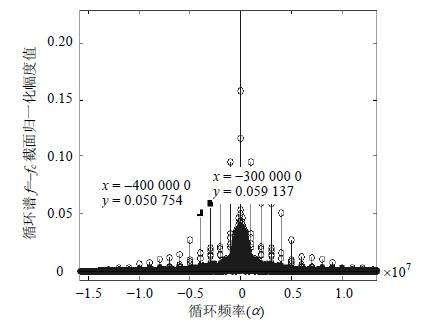 |
| 图7 混叠信号循环谱$f{\rm{ = }} - {f_c}$截面 |
从图 7中可以看到,此时循环谱$f{\rm{ = }} - {f_c}$截面在S2的循环频率处(图中$\alpha {\rm{ = 4}} \times {\rm{1}}{{\rm{0}}^{\rm{6}}}r$)并未出现能量跳变,此时采用能量跳变的方法不能够实现混叠信号检测。
$h_1^2{\rm{/}}h_2^2$变化对混叠信号检测性能影响的曲线如图 8所示。当$h_1^2{\rm{/}}h_2^2 < 0.3$或$h_1^2{\rm{/}}h < 4.5$时,通过循环谱$f{\rm{ = }} - {f_c}$截面能量跳变已无法识别信号是否存在混叠。当$h_1^2{\rm{/}}h_2^2 < 0.3$,其中一个信号在循环谱$f{\rm{ = }} - {f_c}$截面的脉冲值已完全被另一信号淹没;当$h_1^2{\rm{/}}h_2^2 < 4.5$,无法满足能量跳变的条件。该仿真结果验证了能量跳变检测方法所需的条件。
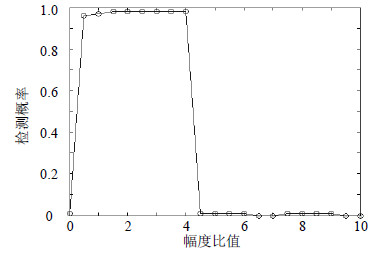 |
| 图8 OFDM信号的识别概率曲线 |
本文针对同频OFDM混叠信号符号速率盲估计问题,提出一种基于信号循环平稳特性的识别方法。分析比较混叠信号和单信号在循环谱上存在的差异,利用这些差异提出了一种通过循环谱在$f{\rm{ = }} - {f_c}$截面切片(脉冲)是否等间隔和是否存在能量跳变来实现混叠信号的识别和符号速率信息的提取,并分析了应用能量条件检测所需的条件。最后通过实验仿真验证了检测方法的有效性和可行性,以及混叠信号幅度差异对检测性能的影响。该方法在混叠信号具有较小频偏时依然有效,当频偏较大时需要进一步研究。
| [1] | 毛欣, 徐慨, 刘杰. 盲信号分离技术现状与发展动态[J]. 通信技术, 2013, 46(8): 24-26. MAO Xin, XU Kai, LIU Jie. Present situation and development of blind signal separation technology[J]. Communications Technology, 2013, 46(8): 24-26. |
| [2] | 路威, 张邦宁, 陆溪. 基于MPSO粒子滤波的单通道扰信盲分离算法[J]. 解放军理工大学学报, 2013, 14(6): 591-596. LU Wei, ZHANG Bang-ning, LU Xi. Single-channel blind separation of communication signal and interference based on MPSO particle filtering[J]. Journal of PLA University of Science and Technology, 2013, 14(6): 591-596. |
| [3] | SHILONG T, HUI Z, NA G. Single-channel blind separation of two QPSK signals using per-survivor processing[C]// Conference on Circuits and Systems, APCCAS 2008 IEEE Asia Pacific. Macao: IEEE Press, 2008. |
| [4] | 赵文红, 王巍. 求解单通道盲分离问题的一种新方法[J]. 计算机科学, 2013, 40(6A): 61-63. ZHAO Wen-hong, WANG Wei. Novel Algorithm for single channel blind separation[J]. Computer Science, 2013, 40(6A): 61-63. |
| [5] | 栾海妍, 江桦, 刘小宝. 利用粒子滤波与支持向量机的数字混合信号单通道盲分离[J]. 应用科学学报, 2011, 29(2): 195-202. LUAN Hai-yan, JIANG Hua, LIU Xiao-bao. Single channel blind source separation of digital mixtures using particle filtering and support vector machine[J]. Journal of Applied Sciences-Electronics and Information Engineering, 2011, 29(2): 195-202. |
| [6] | QISHAN H, QICHONG P. Spectral correlation analysis of OFDM signals[C]// Conference on Information & Communication Technology, 2006, ICICT'06 4th International. Cairo: IEEE Press, 2006. |
| [7] | 蒋清平,杨士中,张天骐. 低信噪比 OFDM 信号符号周期盲估计[J]. 计算机应用, 2010, 30(6): 1463-1465. JIANG Qing-ping, YANG Shi-zhong, ZHANG Tian-qi. Symbol duration blind estimation of OFDM signals with low SNR[J]. Journal of Computer Applications, 2010, 30(6): 1463-1465. |
| [8] | 李彦栓. OFDM信号调制识别与参数估计研究[D]. 西安: 西安电子科技大学, 2012. LI Yan-shuan. Research on the modulation identification and parameter estimation of OFDM signal[D]. Xi'an: Xi'dian University, 2012. |
| [9] | 万坚, 涂世龙. 通信混合信号盲分离理论与技术[M]. 北京: 国防工业出版社, 2012. WAN Jian, TU Shi-long. Theory and technology on blind source separation of communication signal[M]. Beijing: National Defense Industry Press, 2012. |
| [10] | 郭黎利, 李旷代, 石荣, 等.单通道时频重叠双信号的码速率估计方法[J]. 电子信息对抗技术, 2009, 24(1): 34-37. GUO Li-li, LI Kuang-dai, SHI Rong, et al.Method for symbol rate estimation of single-channel time-frequency overlapped two-signals[J]. Electronic Information Warfare Technology, 2009, 24(1): 34-37. |
| [11] | 吴量. 单通道时频混叠信号调制识别与参数估计研究与实现[D]. 郑州: 解放军信息工程大学, 2012. WU Liang. Research on the modulation classification and parameter estimation for single-channel time-frequency overlapped signal and system implementation[D]. Zhengzhou: PLA Information Engineering University, 2012. |
| [12] | 王青红, 彭华, 张金成. 一种基于循环谱的共信道多信号调制参数估计方法[J]. 信号处理, 2011, 27(8): 1153-1159. WANG Qing-hong, PENG Hua, ZHANG Jin-cheng. A method for modulation parameters estimation of co-channel multi-signals based on cyclic spectrum[J]. Signal Processing, 2011, 27(8): 1153-1159. |
| [13] | 于岩, 张旭洲, 李洪义. 一种基于单切面循环谱的MPSK信号的载频的快速估计法[J]. 舰船电子工程, 2013, 33(3): 81-82. YU Yan, ZHANG Xu-zhou, LI Hong-yi. A fast algorithm of carrier frequency based on single profiled SCD for MPSK signals[J]. Ship Electronic Engineering, 2013, 33(3): 81-82. |
| [14] | 何继爱, 裴承全, 浦阳阳. 信号分析与处理的方法研究[J]. 无线通信技术, 2012, 3(2): 12-15. HE Ji-ai, PEI Cheng-quan, PU Yang-yang. Research on signal analysis and processing method[J]. Wireless Communications Technology, 2012, 3(2): 12-15. |
 2015, Vol. 44
2015, Vol. 44
