近年来,地磁导航技术获得了快速的发展,用于导航的地磁信号较为稳定,并且利用地磁场信号本身具有的无源性特点,与其他方式的有源导航相比较而言,地磁导航方法具有明显的优势[1]。如当需要进行导航的主体处于大桥下或者楼宇环境中,仍然可以利用地磁信号进行导航,避免其他导航方式如GPS信号被屏蔽掉的缺点。地磁导航的实质是利用地磁图特征与实时测量到的某些地磁特征信息进行匹配导航的过程[2]。
地磁导航在预定需要导航的区域先测量地磁信号,然后通过插值方法构成地磁图序列,当载体再经过这些预定的区域时,将实测的地磁信号与地磁基准图进行匹配,得出实际位置。由于地磁场的信号比较弱,干扰磁场在地磁测量研究中就显得比较重要[3]。要使匹配结果准确,地磁信号的准确获得是前提,而地磁信号的准确获得取决于传感器的灵敏度准确性以及地磁数据的后续处理算法。传统的地磁导航没有对地磁场特征信息进行多尺度与深层次的分析,而是直接采用相关的数据处理方法对基准地磁图和实测的地磁数据进行匹配,因此有可能导致匹配失准甚至失败[4]。地磁场信号是具有多尺度特征的数据,能够细致地刻画各种细节信息,小波分析方法具有良好的时域和频域优点,可以对信号进行不同尺度的特征提取与分析[5]。使用精度较高的地磁传感器如磁通门获得了地磁信号后,主要对后续数据进行处理。以往的数据处理方法如小波强制降噪将分解后的高频系数全部置为零,这将丢掉部分有用的地磁信息,而小波阈值降噪可以更大限度地获得有用的地磁特征信号,但小波阈值降噪涉及到小波基及阈值的选取问题,目前二者的选取方法大多依靠经验。基于EMD的经验模态分解方法可以有效的克服上述缺点,获得较好的地磁匹配效果。
1 基本原理 1.1 阈值降噪设含有噪声干扰的信号为:
| $ x(k)=f(k)+n(k) $ | (1) |
式中,x(k)为包含噪声的信号;f(k)为真实信号;n(k)为高斯白噪声信号。可以根据小波变换的线性性质对信号进行线性变换,对包含噪声的信号作离散小波变换[6]后得到小波分解系数 ${{d}_{jk}}$。${{d}_{jk}}$由两部分组成,分别是有用信号f(k)对应的小波系数 ${{d}_{y}}(j,k)$与噪声信号n(k)对应的小波系数 $ {{d}_{n}}(j,k)$。小波阈值降噪的主要思路是:对于分解后的系数${{d}_{jk}}$,当其值小于某个阈值时,认为该系数来源于噪声信号,予以忽略;当值大于某个数值时,认为该系数来源于有用信号。有用信号的小波系数有两种处理方法,一是硬阈值方法,即直接将系数${{d}_{jk}}$保留;二是软阈值方法,将系数按照某一原则向零收缩。根据处理后的新小波系数再进行信号重构,可获得去噪后的信号。
1.2 经验模态分解经验模态分解(EMD)[7]是希尔伯特黄变换(HHT)[8]中的一项重要技术,利用EMD的分解方法可以把信号分解成一系列本征模态函数[9]。文献[8]定义了符合两个条件的固有模态函数(IMF):在整个数据序列中,极值点的个数与过零点的个数相等或者相差1;信号上由局部极大值与局部极小值构成的包络线的均值为零[9]。
具体的步骤为,对于信号x(t),先找出它的极大值点,然后利用数学中的三次样条函数进行插值得到上包络线 ${{x}_{\max }}(t)$,同理得到下包络线 ${{x}_{\min }}(t)$。求出这两条包络线的均值 ${{m}_{1}}(t)$,用信号x(t)减去 ${{m}_{1}}(t)$得到 ${{h}_{1}}(t)$[9],即:
| $ {{h}_{1}}(t)=x(t)-{{m}_{1}}(t) $ | (2) |
通常,它并不满足IMF的两个条件,则将 ${{h}_{1}}(t) $看作原信号,重复之前的操作处理步骤得到第k次处理后的 $ {{h}_{k}}(t)$。对于具体求算多少次,需要设定一个终止准则,将两个连续的处理结果之差的标准差SD数值作为处理的终止依据。当 $ {{h}_{k}}(t) $满足终止准则,则为第一阶IMF,记为 $ {{c}_{1}}(t)$,从 $ x(t) $中去掉也就是减去 $ {{c}_{1}}(t)$得到残差 $ {{r}_{1}}(t) $。再把$ {{r}_{1}}(t) $看作新的信号重复上述过程,直到得到了n组残差${{r}_{n}}(t)$。如果此时符合以下条件之一: $ {{r}_{n}}(t) $与 $ {{c}_{n}}(t)$其中之一小于预定的误差;或者 $ {{r}_{n}}(t) $残差成为单调函数,此时就终止模态分解处理过程。到此为止,原始信号 $ x(t) $由n阶IMF分量和残差 $ {{r}_{n}}(t) $构成[10],即:
| $ x(t)=\sum\limits_{i=1}^{n}{{{c}_{i}}(t)+{{r}_{n}}(t)} $ | (3) |
小波阈值处理方法首先需要对小波基和阈值进行选取与设定,但是目前的处理方法中,关于二者的选取与设定通常依靠经验,并没有定量判断的选择准则。EMD分解不需要提前选定分解信号用的基函数,它是根据信号自身的尺度特征,自适应地产生合适的模态函数IMF,并且这些IMF分量有从高频到低频逐次分布的特点[11]。根据以往的经验,噪声分布在信号的高频部分,使用EMD分解出的系数符合从高频到低频依次分布的特点,所以可以通过观察的方法直接将高频系数舍弃。但如前文所说,直接舍弃全部高频系数将丢失掉有用的信号信息,这将直接导致重构信号失准。为避免这种情况发生,可以将小波阈值处理方法运用在EMD分解后的高频系数部分,这样小波阈值处理方法只是作用于信号的高频部分而不是作用于整个信号,EMD处理方法与小波阈值处理方法相互补充,可以更好去噪,从而提取有用的特征信号。
1.4 小波强制降噪与小波阈值降噪小波分解可以将地磁信息分为近似和细节信息,通过增大尺度不断对前一尺度的近似信息进行小波分解。通过信息在各尺度下的变换所实现的信息综合,可以发现信号的特征并使用不同的尺度对细节信息进行更为深层次的描述[12]。对地磁信息 ${{Y}_{n}}$进行分解,得到:
| $ {{Y}_{n}}={{A}_{1}}+(D_{1}^{h}+D_{1}^{v}+D_{1}^{d})={{A}_{s}}+\sum\limits_{s=1}^{S}{(D_{s}^{h}+D_{s}^{v}+S_{s}^{d})} $ | (4) |
近似信息 $ {{A}_{s}} $为初始信息 $ {{Y}_{n}} $在尺度S下的低频信息,是对初始信息 ${{Y}_{n}}$的重要特征的描述;而细节信息 $ D_{s}^{h} $、 $ D_{s}^{v} $、 $ D_{s}^{d} $为初始信息 ${{Y}_{n}}$在尺度S下的有关水平、垂直和对角的高频信息,是对初始信息 $ {{Y}_{n}} $的细节特征所进行的深层次的描述。小波分解结构如图 1所示。其中小波强制去噪与小波阈值去噪的主要差别是:在事先确定的某一尺度的条件下,小波强制降噪方法忽略全部高频信息,仅对低频系数进行重构[13];小波阈值去噪是在一定的规则下对高、低频系数都进行相应的处理后,再进行重构。
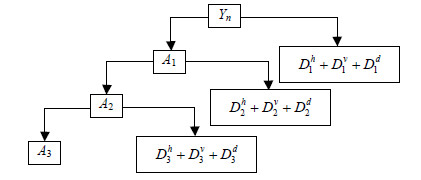 |
| 图1小波分解结构图 |
数据衡量有很多指标,如期望、方差、均方差等,对于地磁数据的匹配结果,应是对所有待匹配点的统一衡量,即所有匹配后的点与真实的航迹点之间的衡量[14],所以数据衡量指标为:
| $ R=\frac{1}{N}\sum\limits_{i=1}^{N}{\sqrt{{{({{Y}_{ix}}-{{F}_{ix}})}^{2}}+{{({{Y}_{iy}}-{{F}_{iy}})}^{2}}}} $ | (5) |
式中, $ {{Y}_{ix}}$和 $ {{Y}_{iy}} $分别为实测的地磁数据经过重构匹配后,其数据点序列 $ {{Y}_{i}} $的经度和纬度值; $ {{F}_{ix}} $和 $ {{F}_{iy}} $分别为真实航迹点序列 $ {{F}_{i}} $的经度和纬度值,由GPS测量得到;R为实测地磁数据经过匹配后的位置与真实航迹点的平均距离,用来衡量匹配后的点序列与真实航迹点序列之间的差异,其值越大,说明匹配误差越大,所以R值称为匹配误差。当R达到最小值时,匹配后的点序列与真实航迹点序列最为接近,或者说匹配后的点序列的经纬度值与真实航迹点的经纬度值最为接近。
2 车载实验验证实验选取地点为北京奥体森林公园附近的路段,车载实验行车路线具体分为两部分,一为闭合行车路线采集地磁数据,通过插值后构成相应的地磁基准图,为地磁匹配提供依据与前提;二为在闭合车载路线中选取一个路径进行实时地磁数据采集,该段路径用于匹配。闭合行车路径为科荟南路-北辰东路-大屯路-天辰西路;具体的待匹配路径选为大屯北路-湖景东路。
2.1 基于EMD的阈值滤波在地磁原始数据中的作用对比本文使用磁通门与陀螺仪组合进行地磁匹配实验,其中磁通门采集地磁信号,陀螺仪采集车的角速度,通过航位推算得到航向角后进行地磁匹配。
磁通门采集的车载实验中的待匹配路径的地磁场总强度,实测数据与经EMD滤波后的数据分别如图 2与图 3所示,图 2为原始测量地磁数据图,图 3为经过EMD小波阈值降噪处理的地磁数据。从图中可以清晰地看出,经过EMD小波阈值降噪后,数据少了很多毛刺与尖峰,信号中的高频噪声明显减少。
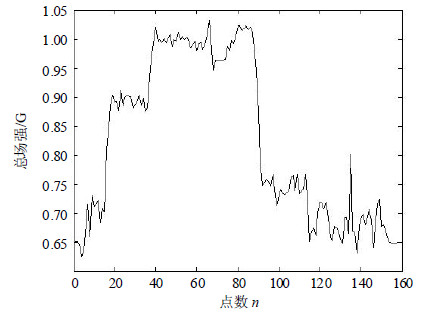 |
| 图2原始测量地磁场强度图 |
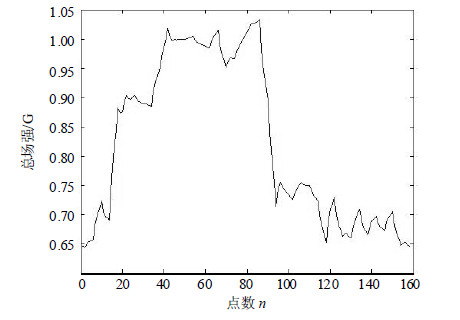 |
| 图3经EMD小波阈值降噪后的地磁场强度图 |
闭合行车路线采集的数据插值后构成地磁基准图,将中间的一条选定的路径作为待匹配路径。首先,对磁通门采集的闭合路径与待匹配路径的地磁场强度的实测数据分别进行小波强制降噪、小波阈值降噪及基于EMD的阈值滤波处理;其次,将3种处理后的闭合路径地磁数据与实测的闭合路径地磁数据均进行插值构成地磁图,插值方法选用Matlab软件中自带的griddata函数,该插值法适用于对离散不规则的多点数据进行插值运算,且更能满足地磁匹配导航的实际情况的要求;最后,将插值后的地磁图分别对应待匹配路径处理后的数据进行匹配,匹配算法选用近年来已成熟运用于地磁匹配方面的ICCP算法[15, 16],匹配后根据式(5)计算匹配误差。上述步骤完成后将3种匹配结果计算出来的匹配误差分别与根据没有处理的实测数据的匹配结果计算的匹配误差进行比较,比较结果如表 1所示。从表 1可知,原始测量数据的匹配误差为4.331 5,经EMD阈值降噪处理后的匹配误差为1.873 9,匹配误差降低了56.74%,可以看出该方法运用在组合导航中取得了较好的效果。
| 表1 不同方法在车辆匹配导航中的结果对比 |
为了更直观地进行比较,将使用原始数据、小波强制降噪后的数据、小波阈值降噪后的数据以及EMD阈值滤波后的匹配结果如图 4~图 7所示。
 |
| 图4地磁测量原始数据匹配结果 |
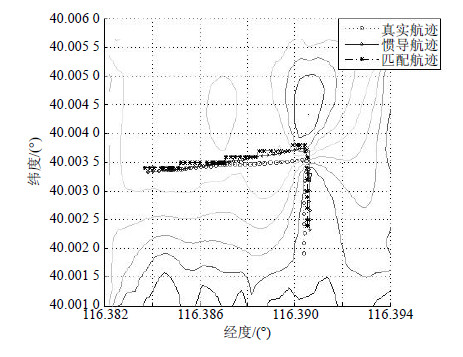 |
| 图5小波强制降噪后的地磁数据匹配结果 |
 |
| 图6小波阈值降噪后的地磁数据匹配结果 |
 |
| 图7基于EMD的阈值降噪后的地磁数据匹配结果 |
通过比较匹配结果图可以得出,3种处理方法中,基于EMD的阈值滤波匹配结果最好,匹配航迹与真实航迹十分接近,大大提高了地磁匹配精度,实验结果说明基于EMD的阈值滤波在地磁匹配中取得了较好的效果。
3 结 论基于EMD的经验模态滤波方法根据信号自身的特点进行分解得到基函数,将包含噪声的高频分量采用小波阈值降噪处理,再与不含噪声的低频分量一起重构原信号,克服了将小波阈值降噪作用于整个信号的缺陷。经过对车载实验中实测的地磁场强度进行小波强制降噪、小波阈值降噪、基于EMD经验模态阈值滤波处理后的数据与实测的地磁数据分别运用griddata函数插值构成地磁图,将待匹配路径运用ICCP算法进行地磁匹配实验,得到实验结果说明小波强制降噪、小波阈值降噪、基于EMD的经验模态滤波方法对于陀螺与磁通门组合的车辆导航地磁匹配都有一定的效果。其中经验模态滤波方法在车载实验中将地磁相对匹配误差降低了56.74%,匹配效果最好。实验结果表明,对实测的地磁场数据运用EMD阈值滤波方法,使地磁数据经过分解、滤波、重构后,地磁的细节特征凸显,解决了地磁测量易受软硬磁干扰导致匹配精度较低甚至匹配失败的问题,有效地提高了地磁匹配导航的精度。
| [1] | 郭才发, 胡正东, 张士峰, 等. 地磁导航综述[J]. 宇航学报, 2009, 30(4): 1314-1318. GUO Cai-fa, HU Zheng-dong, ZHANG Shi-feng, et al. Geomagnetic navigation summary[J]. Journal of Astronautics, 2009, 30(4): 1314-1318. |
| [2] | 李兴城, 张慧心, 张双彪. 地磁导航技术的发展现状[J].飞航导弹, 2013(10) : 80-83. LI Xing-cheng, ZHANG Hui-xin, ZHANG Shuang-biao. The development status of geomagnetic navigation technology[J]. Winged Missiles Journal, 2013(10): 80-83. |
| [3] | 傅慷, 余杰, 钱富. 地磁导航的相关技术研究[J]. 船电技术, 2013, 33(4): 31-33. FU Kang, YU Jie, QIAN Fu. Study on geomagnetic navigation[J]. Marine Electric, 2013, 33(4): 31-33. |
| [4] | 周军, 葛致磊, 施归国, 等. 地磁导航发展与关键技术[J].宇航学报, 2009, 29(5): 1467-1470. ZHOU Jun, GE Zhi-lei, SHI Gui-guo, et al. Key technique and development for geomagnetic navigation[J]. Journal of Astronautics, 2009, 29(5): 1467-1470. |
| [5] | 乔玉坤, 王仕成, 张金生, 等. 小波软阈值降噪的地磁匹配导航仿真研究[J]. 兵工学报, 2011, 32(9): 1083-1087. QIAO Yu-kun, WANG Shi-cheng, ZHANG Jin-sheng, et al. Simulation research on geomagnetic matching navigation based on soft-threshold wavelet denoising method[J]. Acta Armamentarii, 2011, 32(9): 1083-1087. |
| [6] | SANCHEZ E N, PEREZ J P, MARTINEZ M, et al. Chaos stabilization: an inverse optimal control approach[J]. Latin Amer ApplRes IntJ, 2002, 32: 111-114. |
| [7] | CHEN G, DONG X. On feedback control of chaotic continuous-time system[J]. IEEE Trans CAS, Part I, 1993, 40(10): 591-601. |
| [8] | 张晓楠, 曾庆山, 万红. 基于改进小波去噪和EMD方法的轴承故障诊断[J]. 测控技术, 2014, 33(1): 23-26, 30. ZHANG Xiao-nan, ZENG Qing-shan, WAN Hong. Bearing fault diagnosis based on improved wavelet denoising and EMD method[J]. Measurement&Control Technology, 2014, 33(1): 23-26, 30. |
| [9] | 李振兴, 徐洪洲. 基于经验模态分解的小波阈值降噪方法研究[J]. 计算机仿真, 2009, 26(9): 325-337. LI Zhen-xing, XU Hong-zhou. A wavelet threshold de-noising algorithm based on empirical mode decomposition [J]. Computer Simulation, 2009, 26(9): 325-337. |
| [10] | 张敏, 王喜珍, 腾云田, 等. 基于EMD小波阈值滤波的地磁数据去噪分析[J]. 地磁地震观测与研究, 2012, 33(3): 171-172. ZHANG Min, WANG Xi-zhen, TENG Yun-tian, et al. Analysis of wavelet threshold filtering bases on empirical mode decomposition to denoise the geomagnetic data[J]. Seismological and Geomagnetic Observation and Research, 2012, 33(3): 171-172. |
| [11] | 张小清, 张文祥, 刘建霞, 等. 基于EMD和小波阈值滤波降噪的MATLAB仿真[J]. 网络安全技术与应用, 2013(8): 42-43. ZHANG Xiao-qing, ZHANG Wen-xiang, LIU Jian-xia, et al[J]. The MATLAB simulation for empirical mode decomposition and wavelet threshold filtering denoising[J]. Network Security Technology and Applyment, 2013(8): 42-43. |
| [12] | 陈炜. 基于等值线约束的ICCP地磁匹配算法研究[D]. 北京: 北京科技大学, 2014. CHEN Wei. Research of the geomagnetic match algorithm based of contour constraint and ICCP[D]. Beijing: University of Science and Technology Beijing, 2014. |
| [13] | 邢西淳, 邵辉成, 毛娟, 等. 小波变换在地磁数据分析中的应用[J]. 地震地磁观测与研究, 2005, 26(2): 38-41. XING Xi-chun, SHAO Hui-cheng, MAO Juan, et al. Wavelet transform used in geomagnetic data analysis[J]. Seismological and Geomagnetic Observation and Research, 2005, 26(2): 38-41. |
| [14] | 乔玉坤, 张金生, 孙渊, 等. 采用强制降噪和多尺度融合的地磁导航方法[J]. 宇航学报, 2011, 32(1): 53-59. QIAO Yu-kun, ZHANG Jin-sheng, SUN Yuan, et al. A method for geomagnetic matching navigation based on forced de-noising and multi-scale fusion[J]. Journal of Astronautics, 2011, 32(1): 53-59. |
| [15] | 李豫泽, 石志勇, 杨云涛, 等. 基于ICCP算法的地磁匹配定位方法[J]. 现代电子技术, 2008 (20): 122-124. LI Yu-ze, SHI Zhi-yong, YANG Yun-tao, et al. Geomagnetic localization based on ICCP algorithm[J]. Xiandai Dianzi Jishu, 2008(20): 122-124. |
| [16] | 白文平, 王志刚. ICCP重力匹配辅助导航算法研究及改进[J]. 计算机仿真, 2013, 30(6): 15-18. BAI Wen-ping, WANG Zhi-gang. Researching and improving of ICCP algorithm for gravity aided inertial navigation[J]. Computer Simulation, 2013, 30(6): 15-18. |
 2015, Vol. 44
2015, Vol. 44
