秘密分享技术由文献[1, 2]提出,这是一种能更加有效地保障秘密信息安全性的技术。利用秘密分享技术可将秘密信息分解成n个部分,每个部分称作一个子秘密或份额,同时建立特定的规则,即只有满足一定条件(将所有这些条件的集合称作访问结构)的多个份额才能共同恢复出原始秘密信息,因此,秘密分享技术具有非常高的安全性。以一个(k, n)门限秘密分享方案为例(其中k和n均为正整数,且2≤k≤n),即使攻击者截获了一定数目(不多于k)的份额,也不能恢复出原始秘密甚至不能得到关于该秘密的任何信息;当相当数量的子秘密(不多于k个)毁坏或丢失(自然灾害或人为破坏等因素),也不会对秘密的恢复造成任何影响。该技术最初应用于密钥信息的安全保存,将密钥以秘密分享方式分发给多人管理,可以解决密钥管理中的密钥泄漏和遗失问题,提高系统的安全性和稳健性,同时还能够防止权力滥用等问题。秘密分享技术自产生以来就受到了信息安全领域学者们的高度重视,并在过去的30余年间得到了迅速的发展,多种构造秘密分享系统的方案被陆续提出,包括拉格朗日插值多项式方案、多维空间矢量方案、中国剩余定理方案、椭圆曲线方案、矩阵投影方案、编码方案和量子理论方案等[1, 2, 3, 4, 5, 6, 7]。
文献[8]提出的基于拉格朗日插值多项式的门限秘密分享方案以其理论成熟、构造简单和可应用领域广等特点,是目前使用范围最广的秘密分享构造方案。而近年来,随着信息技术的不断进步,对秘密分享的研究和应用也从最初的安全保存文本格式的密钥扩展到了信息安全的诸多领域,例如图像秘密分享、音频秘密分享、视频秘密分享、网络文件传输和分布式文件安全管理等[8, 9, 10, 11, 12, 13, 14, 15, 16, 17]。目前,已有不少基于文献[8]的方案,即使用拉格朗日插值多项式方法构建的应用于多个领域的秘密分享方案被相继提出[9, 10, 11]。但是这些方案在实用化过程中却面临一个很大的障碍,即拉格朗日插值方法的计算复杂度非常高,这对于普通的秘密分享应用(如传统小数量的文本格式密钥分享)影响不大,但是面对大量需要进行秘密分享运算的数据时就会使得整个系统运行速度变得缓慢甚至不可接受。在此背景下,一些学者开始使用编码(主要是删除码)来构建秘密分享方案,在基于编码的秘密分享方案中,份额产生大体可对应编码中码字生成的过程,而秘密重构则可大体对应于编码中的译码过程。其中最具代表性的为文献[14],该文献采用有限域上代数几何编码的方法设计出实用的秘密分享方案,将运算的时间复杂度大大降低。基于此思想,以图像和音频为秘密信息的(k,n)门限秘密分享系统被构造并实现[8, 14, 15, 16, 17]。但是经过分析发现,此类方案(也包括以往几乎所有(k,n)门限的秘密分享方案)在秘密重构过程中仅用到了最低需求的k个份额来进行计算,即使当在秘密重构过程中有k+t个可用份额(t为正整数),系统也只是选取其中的k个份额,而剩余的t个份额并不参与运算而被丢弃。以网络文件多路传输为例,发送端使用秘密分享手段将信息分拆成7个部分,对每个部分使用不同的链路进行传输,设定只需要其中任意4个部分就能够重构原始信息,而假设接收端每次平均能够收到6个链路传输来的正确信息时,问题就出现了:平均每次传输多余门限值的2个信息部分使用了网络带宽,也被正确的传送到了接收端,但是却由于信息重构方法的限制而被白白浪费掉了。因此,充分利用所有的可用份额,将多于门限值的份额用在提高信息重构的运算效率上以提升系统的整体性能是本文研究的目标。基于此,本文在文献[14]方案的基础上提出了一种新的秘密重构方法。
1 相关工作令s表示需要同时进行分享操作的秘密数量,为正整数;L表示单个秘密信息中数据的数量,其单位根据运算的有限域来确定;P表示参与运算信息中的某个确定位置坐标;(k,n)表示秘密分享方案的门限结构参数,其中k和n均为正整数,且满足条件$2\le k\le n$。
此外,所有运算均在有限域$\text{GF}({{2}^{m}})$(m为正整数)上进行,其取值视具体应用场合而定。为了所描述的方案具有普适性,本文认为多个秘密可以同时被分享,即$s\ge 1$,假设s个秘密为${{S}_{1}},{{S}_{2}},\cdots ,{{S}_{s}},s\le k$,且每个秘密所含的信息量相同。
基于编码的秘密分享方案中,份额产生可归纳为6个步骤:
1) 根据(k,n)门限,在有限域$\text{GF}({{2}^{m}})$上构造出矩阵${{\mathbf{G}}_{(n+s)\times k}}$及${{\mathbf{H}}_{(n+s)\times (n+s-k)}}$。构造的具体方法在文献[14]中有非常详细的步骤说明及证明,亦可参考文献[8, 15]相关章节的描述,本文不再赘述。
2) 根据假设,已知s个秘密${{S}_{1}},{{S}_{2}},\cdots ,{{S}_{s}}$,再任意选取$k-s$个和秘密具有相同信息量的数据,则此时共有k个信息,记作${{V}_{1}},{{V}_{2}},\cdots ,{{V}_{k}}$。
3) 根据一定规则(可以是顺序也可以按照某种原则非顺序),从s个秘密信息中确定一取值点P,对上述每一个${{V}_{i}}$取出其在位置P处的数据值${{a}_{i}},{{a}_{i}}\in \text{GF}({{2}^{m}})$,构成一个由k个数值组成的序列${{({{a}_{1}},{{a}_{2}},\cdots ,{{a}_{k}})}^{\text{T}}}$,记作信息矢${{\alpha }_{k\times 1}}$。
4) 使用步骤1)中构造的矩阵${{\mathbf{G}}_{(n+s)\times k}}$对步骤3)中确定的信息矢${{\alpha }_{k\times 1}}$进行编码,得到码字${{\mathbf{\beta }}_{(n+s)\times 1}}$,${{\beta }_{(n+s)\times 1}}={{G}_{(n+s)\times k}}{{\alpha }_{k\times 1}}$。上述编码运算均在有限域中$\text{GF}({{2}^{m}})$进行。由于${{\mathbf{G}}_{(n+s)\times k}}$是系统码的生成矩阵,故码字$\beta $的前k个分量与$\alpha $完全相同,即$\mathbf{\beta }=({{a}_{1}},{{a}_{2}},\cdots ,{{a}_{k}},{{b}_{k+1}},{{b}_{k+2}},\cdots ,{{b}_{k+((n+s)-k)}})$。
5) 将信息矢${{\alpha }_{k\times 1}}$前s个元素销毁,并将其余n个值${{a}_{s+1}},{{a}_{s+2}},\cdots ,{{a}_{k}},{{b}_{k+1}},{{b}_{k+2}},\cdots ,{{b}_{k+((n+s)-k)}}$中的${{b}_{k+1}},{{b}_{k+2}},$ $\cdots ,{{b}_{k+((n+s)-k)}}$作为$n+s-k$个份额的一部分。
6) 按指定顺序遍历L个位置P,重复上述过程即可得到$n+s-k$个份额,连同步骤2)中选取的$k-s$个信息,得到全部n个份额。
当聚集≥k个份额时,就可以对秘密进行重构。其具体步骤为:
1) 原始的份额记作${{D}_{1}},{{D}_{2}},\cdots ,{{D}_{n}}$,将任意份额${{D}_{j}}$的采样点数值记为${{b}_{1,P}},{{b}_{2,P}},\cdots ,{{b}_{n+s,P}}$,${{b}_{i,P}}\in \text{GF}({{2}^{m}})$$i=1,2,\cdots ,$$n+s$。按照份额产生的顺序坐标位置统一排序,取当前坐标位置P,按以下步骤在P处恢复s个秘密${{V}_{1}},{{V}_{2}},\cdots ,{{V}_{s}}$在对应位置的数据值。
2) 将s个秘密和n个份额在P处对应的数据值分别记为${{b}_{1,P}},{{b}_{2,P}},\cdots ,{{b}_{n+s,P}}$,${{b}_{i,P}}\in \text{GF}({{2}^{m}})$,$i=1,2,\cdots ,$ n+s。令${{\mathbf{\beta }}_{(n+s)\times 1}}={{({{b}_{1,P}},{{b}_{2,P}},\cdots ,{{b}_{n+s,P}})}^{\text{T}}}$,其中有k个数值${{b}_{i,P}}$已知,$i=1,2\cdots ,k$,而其余$n+s-k$个数值未知。因为${{\mathbf{\beta }}_{(n+s)\times 1}}={{\mathbf{G}}_{(n+s)\times k}}{{\mathbf{\alpha }}_{k\times 1}}$,且矩阵${{\mathbf{H}}_{(n+s)\times (n+s-k)}}$的诸列向量正交于矩阵${{\mathbf{G}}_{(n+s)\times k}}$中诸列向量张成的线性子空间,因此有下列等式成立:$\mathbf{H}_{(n+s)\times (n+s-k)}^{\text{T}}{{\mathbf{\beta }}_{(n+s)\times 1}}={{\mathbf{\theta }}_{(n+s-k)\times 1}}$。由此得到方程组:
| $\left. \begin{matrix} {{b}_{1,P}} & + & {{b}_{2,P}} & + & \cdots & + & {{b}_{n+s,P}} & = & 0 \\ {{a}_{1}}{{b}_{1,P}} & + & {{a}_{2}}{{b}_{2,P}} & + & \cdots & + & {{a}_{n+s}}{{b}_{n+s,P}} & = & 0 \\ \vdots & {} & \vdots & {} & \vdots & {} & \vdots & = & \vdots \\ a_{1}^{n+s-k-1}{{b}_{1,P}} & + & a_{2}^{n+s-k-1}{{b}_{2,P}} & + & \cdots & + & a_{n+s}^{n+s-k-1}{{b}_{n+s,P}} & = & 0 \\ \end{matrix} \right\}$ | (1) |
由于其中k个数值${{b}_{i,P}}$为已知($i=1,2,\cdots ,k$),将它们代入式(1),可得到:
| ${{\mathbf{A}}_{(n+s-k)(n+s-k)}}\mathbf{\gamma }=\mathbf{\eta }$ | (2) |
3) 根据份额产生时的规则,遍历位置$P=1,2,\cdots ,L$,重复步骤2),即可重构出最初s个秘密信息。
2 新的秘密重构方法基于编码的秘密分享方案中,份额生成时主要使用的是有限域上的矩阵乘法,因此在实现时可以采用缩小运算有限域等手段和技巧提高计算效率(相关内容文献[8]中已有详细的论述),而在秘密重构计算时主要使用的方法为有限域上的矩阵求逆运算,算法复杂度高且不能应用份额生成时的效率优化方法。因此,无论是从算法的复杂度还是从实际效果而言,秘密重构花费的时间要远远大于份额产生的时间。但是在秘密重构的过程中,如果可用的份额数量超过k个,在实际运算时也只是利用到了其中的k个,多余门限值的份额将被闲置和浪费。
与文献[8, 14, 15, 16, 17]相似,在本文秘密重构方法中所有运算使用的有限域仍然采用比特矩阵构建的有限域,除了理论体系成熟、运算效率高、代码实现便捷等优点,选用此类有限域的重要原因是该有限域中每个元素的加法逆元是该元素本身,即相同元素的和为该有限域中的零元素,这一特性也是本文方法的正确性保障。
n个份额记作${{D}_{1}},{{D}_{2}},\cdots ,{{D}_{n}}$,假设在秘密重构时存在t个份额可用,其中不等式${{D}_{i}},{{D}_{i+1}},\cdots ,{{D}_{i+t-1}}$成立,否则秘密无法重构。为了表述方便,不妨将这t个份额记作${{D}_{j}},{{D}_{j+1}},\cdots ,{{D}_{j+n-t-1}}$,而将另外不可用的$n-t$个份额记作${{D}_{j}},{{D}_{j+1}},\cdots ,{{D}_{j+n-t-1}}$,特别说明的是,此处份额下标和份额本身的顺序编号无严格的对应意义,仅表示在秘密重构时的t个可用份额和$n-t$个未知份额。此外,仍然假设有s个秘密需要重构,用${{a}_{1}},{{a}_{2}},\cdots ,{{a}_{s}}$分别表示s个秘密在某个特定位置P上的数值。
方法的具体步骤为:
1) 按照份额本身的顺序编号对所有份额进行排序,并将其置于${{a}_{1}},{{a}_{2}}\cdots ,{{a}_{s}}$之后,形成一个具有$s+n$个元素的向量,记作X,用来对应一致校验矩阵H的各个列。
2) 将向量X中的各个元素进行分类,将已知元素和未知元素分别集中放置于向量X的左边和右边,记作$X=\{d|y\}$,其中d表示全部的已知元素,而y表示全部的未知元素,而${{a}_{1}},{{a}_{2}}\cdots ,{{a}_{s}}$也包含其中。
3) 根据X中的各个元素与矩阵H各列的位置对
应关系,将矩阵H中的各列也相应地重新排列后记作$H=\{A|B\}$,其中子矩阵A的各列对应子向量d的各个元素,而子矩阵B的各列则对应子向量y的各个元素。
4) 假设子矩阵B共有m列(m一定小于等于门限值k,否则秘密无法重构),找出矩阵B中任意一组线性无关的m行,形成矩阵$\bar{B}$。
5) 将矩阵A与矩阵$\bar{B}$中各行与在矩阵B中有相同行编号的各行抽取出来,形成子矩阵$\bar{A}$。
6) 计算$y=\bar{B}\bar{A}d$,可得s个秘密在在位置P处的数值${{a}_{1}},{{a}_{2}},\cdots ,{{a}_{s}}$。
根据份额产生时的规则,遍历位置$P=1,2,\cdots ,L$,重复步骤6),即可重构出最初s个秘密信息。
3 分析与对比首先证明新方法的正确性。
证明:在基于编码的秘密分享方案中,所有的秘密数据均作为编码运算中原始数据的一部分,因此,在前面步骤1)中的向量X可以认为是编码后产生的码字。如前所述,矩阵H可以认定为有限域上的校验矩阵(其具体构造及证明过程内容较多,详细请参考文献[14]),因此等式$HX=0$一定成立。按照前文所述,向量X的元素和矩阵H的列向量都重新进行了排序,并分别记作$X=\{d|y\}$和$H=\{A|B\}$。由矩阵及分块矩阵运算规则可得下列等式成立:$Ad+By=0$;整个运算体系使用的有限域具有元素为自身加法逆元的特性,因此可得等式$Ad=By$成立。而$\bar{B}$和$\bar{A}$分别为矩阵B和A的子矩阵,且具有行对应关系,因而有等式$\bar{A}d=\bar{B}y$成立。而$\bar{B}$同时又是矩阵H的子矩阵,所以$\bar{B}$一定可逆。所以,新的方法可以正确重构出秘密信息。证毕。
基于编码的秘密分享方案中,文献[14]给出了具有代表性的秘密重构方法,该方法也是当前基于编码秘密分享的最常用方法,而本文则提出了一种新的秘密重构方法。两种秘密重构方法均使用到了有限域上的矩阵求逆运算(整个秘密重构过程中计算量最大的操作),而最大的区别在于对份额的利用上,文献[14]中的方法在秘密重构时无论有多少个可用份额,均假定可用份额数量为k,即从可用份额中任意选用其中的k个(满足门限条件),新的方法则利用了在秘密重构时全部的已知份额,且在秘密重构时可利用的份额越多,需要进行求逆运算的矩阵规模就越小,从而减少秘密重构的整体计算量。
由于字节是大多计算机运算的实际最小单位,为了便于计算量统计,因而在不失一般性的前提下假设所有运算的有限域为$\text{GF}({{2}^{8}})$,在秘密重构时获得的可用份额数量等概率随机取自k到n,其中$0 < k\le n < {{2}^{8}}$。前面所述的两种方法对于每一个秘密中某特定位置数据进行计算的时间复杂度对比如图 1所示。而使用本文方法在对秘密进行重构时,运算量将随着已知份额数量的增大而不断降低;由前面算法描述不难看出,有限域上的矩阵求逆运算为整个秘密重构过程的最大工作量部分,而新方法的核心即通过份额数量的增加有效减少求逆运算的工作量。图 2中分别以(2,5)、(3,8)、(5,9)和(9,17)门限结构为例说明了使用新方法恢复秘密中某个特定位置数据时,随着可用份额增多后求逆计算量的下降情况。
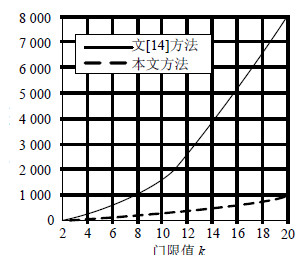 |
| 图1 平均计算复杂度对比 |
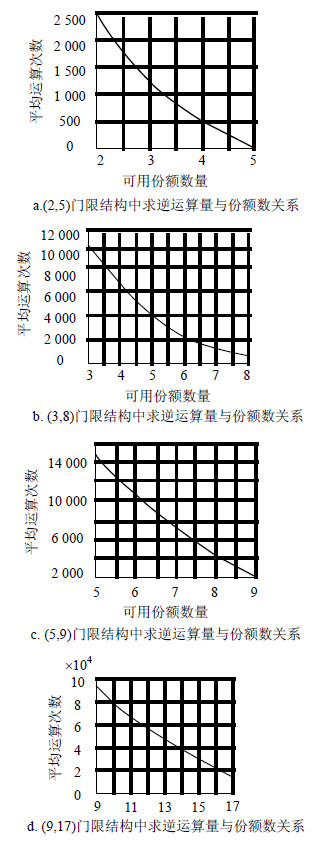 |
| 图2 本文方法的求逆运算总量与份额数量关系 |
基于编码理论的秘密分享方案现在已经广泛的应用于信息安全的诸多领域,如图像秘密分享、音频秘密分享、分布式文件安全管理以及P2P文件传输等。针对当前已有的方案,本文提出了一种新的秘密重构方法,该方法能充分利用所有的可用份额来减少运算量,而经过试验及分析表明新的方法大大降低了秘密重构的计算复杂度,这对于网络中的多路传输系统等相关应用尤为重要。此外,该方法并不改变当前主流方案的核心思想,因此现有系统能非常便捷的将本方法嵌入到已有的实用系统中,也具有一定的现实意义。
| [1] | SHAMIR A. How to share a secret[J]. Communications of the ACM, 1979, 22(11): 612-613. |
| [2] | BLAKLEY G. Safeguarding cryptographic keys[C]//Proceedings of the National Computer Conference. New York, USA: Wiley, 1979. |
| [3] | ASMUTH C, BLOOM J. A modular approach to key safeguarding[J]. IEEE Transactions on Information Theory, 1983, 29(2): 208-210. |
| [4] | CHEN H, LING S, XIANG C P. Access sturctures of elliptic secret sharing schemes[J]. IEEE Transaction on Information Theory, 2008, 54(2): 850-852. |
| [5] | YANG Y G, WEN Q Y, ZHU F C. An efficient two-step quantum key distribution protocol with orthogonal product states[J]. Chinese Physics, 2007, 16(4): 910-914. |
| [6] | MCELIECE R J, SARWATE D V. On sharing secrets and reed-solomon codes[J]. Communications of the ACM, 1981(9): 583-584. |
| [7] | LI Bai. A reliable (k,n) image secret sharing seheme. dependable, autonomic and secure computing[C]//2nd IEEE International Symposium on Dependable, Autonomic and Secure Computing. Indianapolis, USA: Hans-Andrea Loeliger, 2006. |
| [8] | 唐聃. 图像秘密分享技术研究[D]. 北京: 中国科学院, 2010. TANG Dan. Research on secret image sharing scheme[D]. Beijing: Chinese Academy of Sciences, 2010. |
| [9] | THIEN C C, LIN J C. Secret image sharing[J]. Computer & Graphic, 2002, 26(5): 765-770. |
| [10] | MOL J J D, POUWELSE J A, EPEMA D H J, et al. Free-riding, fairness, and firewalls in P2P file-sharing in peer-to-peer computing[C]//Eighth International Conference on P2P. Aachen, Germany: [s.n.], 2008. |
| [11] | LEIN H, LIN Chang-lu. Asynchronous secret reconstruction and its application to the threshold cryptography[J]. International Journal of Communications, Network and System Sciences, 2014, 7(1): 22-29. |
| [12] | MASSEY J L. Minimal codewords and secret sharing[C]//Proceedings of the Joint Swedish-Russian International Workshop on Information Theory. Sweden: Willy, 1993. |
| [13] | BLAKLEY G R, KABATIANSKI G A. Ideal perfect threshold schemes and MDS codes[C]//Proceedings of the International Symposium on Information Theory. Washington, USA: Springer, 1995. |
| [14] | 王晓京, 方佳嘉, 蔡红亮, 等. 视图的秘密分享及其代 数编码方法[J]. 计算机应用, 2012, 32(3): 669-678. WANG Xiao-jing, FANG Jia-jia, CAI Hong-liang, et al. Secret image sharing and its algebraic coding method[J]. Journal of Computer Applications, 2012, 32(3): 669-678. |
| [15] | 王一丁. 音频秘密分享技术研究[D]. 北京: 中国科学院, 2011. WANG Yi-ding. Research on secret audio sharing scheme[D]. Beijing: Chinese Academy of Sciences, 2011. |
| [16] | 方佳嘉. 感官信息秘密分享技术及其应用研究[D]. 北京: 中国科学院, 2012. FANG Jia-jia. Research on sensory information secret sharing and its applications[D]. Beijing: Chinese Academy of Sciences, 2012. |
| [17] | 唐聃, 王晓京. 基于编码理论的图像秘密分享技术研究[J]. 计算机应用与软件, 2013, 30(9): 141-146. TANG Dan, WANG Xiao-jing. Research on secret sharing of image based on coding theory[J]. Computer Applications and Software, 2013, 30(9): 141-146. |
 2016, Vol. 45
2016, Vol. 45
