2. 电子科技大学通信与信息工程学院 成都 611731
2. School of Communication and Information Engineering, University of Electronic Science and Technology of China Chengdu 611731
随着无线网络的飞速发展以及无线设备的大量使用,无线通信中的安全问题引起了人们的广泛关注。由于无线通信的广播特性,很容易受到窃听、消息篡改、节点冒充等攻击。为了实现信息的可靠性、完整性和认证性,必须在通信之前实现密钥的安全分配。一方面,由于无线设备往往是电池供能,且计算能力较弱,这使得现有的基于传统密码学方法的密钥分配协议(现有的密钥分配协议通常采用可信第三方体系或者公钥体系,如常用的Diffie- Hellman协议[1],其特点是计算量大、能耗高)面临着巨大的挑战。另一方面,随着计算机的高速发展以及云计算[2]等新领域的兴起,敌手可获取的计算能力不断提高,这也使得基于计算安全的密钥分配算法不再满足人们对安全的需求。因此,寻求一种计算量小、能耗低且安全性高的密钥分配协议已显得尤为重要。
1 基于物理层的密钥分配协议概述目前,基于物理层的密钥分配协议[3-10]是解决无线安全中上述难题的可行方法之一。该方法利用通信双方的无线信道特征[3],通过测量刻画信道多径效应的物理量(如信道增益、相位平移、接收信号强度等)产生密钥。这些信道特征包括:1)无线信道的时变性:由于多径效应使得信道衰落随着时间而随机变化,且具有较强的随机性;2)无线信道的空变性:在不同空间位置两个链接的终端的无线信道是独立的;3)无线信道的自反性:无线信道的多径特征(如信道增益、相位平移、时延等)在链路的两个方向都是相关的、一致的。基于上述观察,发现在无线通信中存在自然的“随机源”(无线信道的物理特征:信道增益、相位平移、时延等)用于密钥提取,且利用这种随机源能够帮实现信息论安全。
现存的基于物理层的密钥提取方案存在着诸多限制,如密钥率低、密钥熵值低、依赖节点或者环境的移动性。目前最高的密钥生成效率只有40 bits/s[7],达到这一效率要求节点的移动性,且在协议双方还造成了4%的比特错误。造成这一现象的原因是现存的协议依赖信道变化,即如果信道不发生变化就不能产生新的密钥。在静止的环境中信道变化是非常缓慢的,这就使得这些协议不能应用在静止的环境中。根据分析[5],在静止的环境中窃听者可以判断出密钥信息,这使得密钥的安全性得不到保障。文献[11]引入了一种信道独立的物理层方法来提高信道的变化率。该协议的安全性是基于OFDM系统的数据传输的统计特性实现的,所以该协议并不适用于其他通信系统。
为了解决这一问题,文献[12]提出了通过两根天线改变信道的随机性来提高密钥速率。该协议同时假设敌手也是多天线的,且对敌手天线的数量没有限制。本文中通过实验数据分析指出,对于多天线的敌手,该协议是安全的。但作者并没有证明该协议是信息论安全的。那么该协议是否能在信息论安全的前提下提高密钥生成效率呢?
本文从信息论的角度出发,通过理论证明:文献[12]所提出协议在多天线敌手的前提下,协议中通过改变信道的随机性并不能增加密钥的信息熵。因此,该协议不能实现信息论安全的同时提高密钥生成效率的理论上界。故该协议不是信息论安全的。
2 基于虚拟信道的密钥生成协议 2.1 系统模型无线通信中,合法用户Alice和Bob在敌手Eve窃听信道的情况下,要实现安全对称密钥的分发来达到安全通信。本文假设Eve知道合法用户间的通信协议,且可以对接收到的信号所在的信道进行信道测量[13];同时假设Alice具有两根天线,Bob有一根天线,而Eve具有多根天线,如图 1[12]所示,将天线按顺序1, 2, …, k编号。假设通信方式为窄带通信,其结果可以自然地推广到宽带通信。还假设通信信道是相互关联的,即前向信道(从Alice到Bob)和反向信道(从Bob到Alice)的信道增益在相干时间内是相等的。记
 |
| 图1 系统模型 |
信道探测方式:当发送方Alice发送已知探测包x[m],Alice用
| ${y_{{\rm{AB}}}}[m] = (\sqrt \alpha {{\rm{e}}^{{\rm{j}}\theta {{\kern 1pt} _1}}}{h_{{\kern 1pt} 13}} + \sqrt {1 - \alpha } {{\rm{e}}^{{\rm{j}}{\theta _{{\kern 1pt} 2}}}}{h_{{\kern 1pt} 23}})x[m] + {\omega _{{\rm{AB}}}}$ | (1) |
式中,
为了简化模型,本文只考虑小尺度衰落,没有考虑路径长度对协议的影响,但结论同样适用于大尺度衰落。
同时,敌手Eve的第k根天线所接收到的信号可表示为:
| $ {y_{{\rm{A}}{{\rm{E}}^{{\kern 1pt} k}}}}[m] = (\sqrt \alpha {{\rm{e}}^{{\rm{j}}\theta {{\kern 1pt} _1}}}h{{\kern 1pt} _{1k}} + \sqrt {1 - \alpha } {{\rm{e}}^{{\rm{j}}\theta {{\kern 1pt} _2}}}{h_{{\kern 1pt} 2k}})x[m] + {\omega _{{\rm{A}}{{\rm{E}}^{{\kern 1pt} k}}}} $ | (2) |
式中,
从式(1)可以得出,Alice的两根天线到Bob合成的信道增益可以表示为:
| $ {\mathit{\boldsymbol{h}}_{{\rm{AB}}}} = \sqrt \alpha {{\rm{e}}^{{\rm{j}}{\theta _1}}}{h_{13}}{\rm{ + }}\sqrt {1 - \alpha } {{\rm{e}}^{{\rm{j}}{\theta _2}}}{h_{23}} $ | (3) |
称
关于基于虚拟信道的密钥生成协议的详细阐述,请参考文献[12]。该协议主要包括虚拟信道测量和测量值的量化两个阶段。
虚拟信道测量阶段:首先,Alice确定L组三维向量
| ${\mathit{\boldsymbol{h}}_{{\rm{AB}}}} = [{h_{{\rm{AB}}}}(1),{h_{{\rm{AB}}}}(2), \cdots \;,{h_{{\rm{AB}}}}(L)]$ | (4) |
其次,对每一组
| $ \mathit{\boldsymbol{h}}_{{\rm{AB}}}^* = [h_{{\rm{AB}}}^*(1),h_{{\rm{AB}}}^*(2), \cdots \;,h_{{\rm{AB}}}^*(L)] $ | (5) |
测量值的量化阶段:记
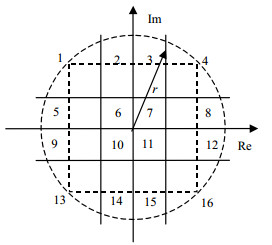 |
| 图2 量化区域的划分 |
在信息论中,信息熵刻画了一个随机变量的不确定程度。记
| $ H(X) = \int_S {f(X)} \log f(x){\rm{d}}x $ |
式中,
传统的密码学的安全性都是基于某一个计算假设,称之为计算安全,如常用公钥密码体系RSA,其安全性是基于“大整数的因式分解是NP问题”。计算安全的弱点包括:1)假设敌手的计算能力是有限的。当敌手的计算能力在假设的范围内,系统是安全的;当敌手的计算能力高于假设,则系统将不再安全。2)计算安全的安全性验证是基于复杂性理论,而一个问题的复杂度是由最极端的情况决定的,即存在这样的情况:虽然问题的复杂度很高,但对于该问题的某些情况甚至很大一部分情况的复杂度却是比较低的。3)随着“云计算”的不断发展,人们所拥有计算能力也在不断提高,这对计算安全的系统是一个巨大的挑战。4)量子计算的飞速发展,使得基于量子计算模型的量子计算机逐步成为可能。大量研究证明在图灵机模型下许多NP问题在量子计算模型下具有快速算法。
如果一个密码体系从信息论的角度是安全的,称之为信息论安全[14]。信息论安全的密码体系假设敌手具有无限计算能力,也称之为无条件安全。显然,信息论安全是比计算安全更强的安全定义。
定义1 称随机变量
文献[15]给出了基于物理层安全的密钥分配协议的生成密钥率的理论上界。这里的密钥率指的是单位时间内生成密钥的比特数。该上界可表示为:在给定敌手Eve已知信息的条件下,Alice和Bob在单位时间内的所得到的信息的条件互信息。
如果将传统的基于多天线的物理层的密钥分配协议[16]应用到本文中的通信模型(即Alice两根天线,Bob一根天线),容易证明其理论上界为:
| $ \frac{1}{{{T_{\rm{C}}}}}[H({h_{13}}) + H({h_{23}})] $ |
式中,
当敌手Eve的天线数目大于等于
下面的定理是本文的主要结论。
定理1 当敌手的天线数大于
| ${R_M} \leqslant \frac{1}{{{T_{\rm{C}}}}}[H({h_{13}}) + H({h_{23}})]$ | (6) |
式中,
| $ {R_M} \leqslant \frac{1}{{{T_{\rm{C}}}}}\ln 2{\rm{ \mathsf{ π} e}}\sigma _{13}^{}\sigma _{23} $ |
证明:不妨假设Eve有两根天线,即
| $ {R_M} = \frac{1}{{{T_{\rm{C}}}}}{\rm{I}}(\mathit{\boldsymbol{h}}_{{\rm{AB}}}^{}{\rm{,}}{\kern 1pt} \mathit{\boldsymbol{h}}_{{\rm{AB}}}^*{\rm{|View(Eve)}}) $ | (7) |
式中,View(Eve)表示Eve所能得到的所有信息。
对于每一个对于
| $ h_{{\rm{AB}}}^*(l) = {h_{{\rm{AB}}}}(l) = {h_{13}}a(l) + {h_{23}}b(l) $ |
令:
故式(7)可改写成:
| $\begin{gathered} \;{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{{T_{\rm{C}}}}}H{\rm{(}}\mathit{\boldsymbol{h}}_{{\rm{AB}}}^{}{\rm{|View(Eve)) - }}H{\rm{(}}\mathit{\boldsymbol{h}}_{{\rm{AB}}}^{}|\mathit{\boldsymbol{h}}_{{\rm{AB}}}^{\rm{*}}{\rm{View(Eve))}} = \\ \frac{1}{{{T_{\rm{C}}}}}H{\rm{(}}\mathit{\boldsymbol{h}}_{{\rm{AB}}}^{}{\rm{|View(Eve))}} \\ \end{gathered} $ | (8) |
同样的,Eve可以利用监听到的信号集(如等式(3)所示)采用相同的信道评估方法计算出如下结果:
| $\left\{ \begin{gathered} h_{{\rm{A}}{{\rm{E}}^4}}^{}(l) = {h_{14}}a(l) + {h_{24}}b(l) \hfill \\ h_{{\rm{A}}{{\rm{E}}^5}}^{}(l) = {h_{15}}a(l) + {h_{25}}b(l) \hfill \\ \end{gathered} \right.{\kern 1pt} $ | (9) |
在静态的环境下(此时,相干时间
解线性方程组(9)可得到:
| $\left\{ \begin{gathered} a(l) = \frac{{{h_{25}}h_{{\rm{A}}{{\rm{E}}^4}}^{}(l) - {h_{24}}h_{{\rm{A}}{{\rm{E}}^5}}^{}(l)}}{{{h_{14}}{h_{25}} - {h_{15}}{h_{24}}}} \hfill \\ b(l) = \frac{{{h_{15}}h_{{\rm{A}}{{\rm{E}}^4}}^{}(l) - {h_{14}}h_{{\rm{A}}{{\rm{E}}^5}}^{}(l)}}{{{h_{15}}{h_{24}} - {h_{14}}{h_{25}}}} \hfill \\ \end{gathered} \right.{\kern 1pt} $ | (10) |
故可将等式(8)改写为:
| $ \begin{gathered} \;\frac{1}{{{T_{\rm{C}}}}}H{\rm{(}}\mathit{\boldsymbol{h}}_{{\rm{AB}}}^{}{\rm{|View(Eve))}} = \\ \frac{1}{{{T_{\rm{C}}}}}H{\rm{(}}\mathit{\boldsymbol{h}}_{{\rm{AB}}}^{}{\rm{|View(Eve),\{ }}a(l){\rm{\} }}_{l{\rm{ = 1}}}^L{\rm{,\{ }}b{\rm{(}}l{\rm{)\} }}_{l{\rm{ = 1}}}^L{\rm{)}} \leqslant \\ \frac{1}{{{T_{\rm{C}}}}}H{\rm{(}}\mathit{\boldsymbol{h}}_{{\rm{AB}}}^{}{\rm{|\{ }}a(l){\rm{\} }}_{l{\rm{ = 1}}}^L{\rm{,\{ }}b{\rm{(}}l{\rm{)\} }}_{l{\rm{ = 1}}}^L{\rm{)}} = \\ \frac{1}{{{T_{\rm{C}}}}}H{\rm{(}}\{ {h_{13}}a(l) + {h_{23}}b(l)\} _{l{\rm{ = 1}}}^L{\rm{|\{ }}a(l){\rm{\} }}_{l{\rm{ = 1}}}^L{\rm{,\{ }}b{\rm{(}}l{\rm{)\} }}_{l{\rm{ = 1}}}^L{\rm{)}} \leqslant \\ \frac{1}{{{T_{\rm{C}}}}}H{\rm{(}}\{ {h_{13}},{h_{23}}{\rm{|\{ }}a(l){\rm{\} }}_{l{\rm{ = 1}}}^L{\rm{,\{ }}b{\rm{(}}l{\rm{)\} }}_{l{\rm{ = 1}}}^L{\rm{) = }} \\ \frac{1}{{{T_{\rm{C}}}}}{\rm{[}}H{\rm{(}}{h_{13}}) + H({h_{23}}{\rm{)]}} \\ \end{gathered} $ |
其中,最后一个等式成立的原因是序列
如果
| $\begin{gathered} \ \ \ {R_M} \leqslant \frac{1}{{{T_{\rm{C}}}}}{\rm{[}}H{\rm{(}}{h_{13}}) + H({h_{23}}{\rm{)] = }} \\ \frac{1}{{{T_{\rm{C}}}}}\left[ {\frac{1}{2}\ln 2{\rm{ \mathsf{ π} e}}\sigma _{13}^2 + \frac{1}{2}\ln 2{\rm{ \mathsf{ π} e}}\sigma _{23}^2} \right]{\rm{ = }} \\ \frac{1}{{{T_{\rm{C}}}}}\ln 2{\rm{ \mathsf{ π} e}}\sigma _{13}^{}\sigma _{23}^{}\quad \quad \quad \quad \quad \\ \end{gathered} $ |
证毕。
上述定理说明在多天线敌手的场景下,利用虚拟信道来实现信息论安全的密钥分配在理论上不能增加密钥的生成效率。进一步,基于虚拟信道的密钥分配协议所产生的密钥只用到了Alice和Bob间的两个信道的信道增益的熵(不确定性),而随机向量组
在基于物理层的密钥分配的研究领域中,如何针对多天线的敌手(特别是天线大于密钥协商方的时候)实现信息论安全的高效密钥分配一直是该领域的一个研究难点。本文从信息论的角度出发,发现文献[12]所提出的密钥分配协议并不是信息论安全的。今后,将对多天线敌手下的信息论安全的快速密钥分配协议的设计进行研究。
| [1] |
DIFFIE W, HELLMAN M. New directions in cryptography[J].
IEEE Transactions on Information Theory, 1976, 22(6): 644–654.
DOI:10.1109/TIT.1976.1055638 |
| [2] |
ARMBRUST M, FOX A, GRIFFITH R, et al. A view of cloud computing[J].
Communications of the ACM, 2010, 53(4): 50–58.
|
| [3] |
AZIMI-SADIADI B, KIAYIAS A, MERCADO A, et al. Robust key generation from signal envelopes in wireless networks[C]//Proceedings of ACM CCS. [S. l]: ACM, 2007: 401-410.
|
| [4] |
MATHUR S, TRAPPE W, MANDAYAM N, et al. Radio-telepathy: Extracting a secret key from an unauthenticated wireless channel[C]//Proceedings of ACM Mobicom. [S. l]: ACM, 2008: 128-139.
|
| [5] |
JANA S, PREMNATH S N, CLARK M, et al. On the effectiveness of secret key extraction from wireless signal strength in real environments[C]//Proceedings of ACM Mobicom. [S. l. ]: ACM, 2009: 321-332.
|
| [6] |
PATWARI N, CROFT J, JANA S, et al. High-rate uncorrelated bit extraction for shared secret key generation from channel measurements[J].
IEEE Transactions on Wireless Communication, 2010, 9(1): 17–30.
|
| [7] |
CROFT J, PATWARI N, KASERA S K. Robust uncorrelated bit extraction methodologies for wireless sensors[C]// Proceedings of ACM/IEEE ICNP. [S. l. ]: [s. n. ], 2010: 70-81.
|
| [8] |
CHEN D J, QIN Z, MAO X F, et al. SmokeGrenade: an efficient key generation protocol with artificial interference[J].
IEEE Transactions on Information Forensics & Security, 2013, 8(11): 1731–1745.
|
| [9] |
WANG Q, SU H, REN K, et al. Fast and scalable secret key generation exploiting channel phase randomness in wireless networks[C]//Proceedings of IEEE INFOCOM. [S. l. ]: IEEE, 2011: 1422-1430.
|
| [10] |
CHEN D J, MAO X F, QIN Z, et al. SmokeGrenade: a key generation protocol with artificial interference in wireless networks[C]//Proceedings of IEEE MASS. [S. l. ]: IEEE, 2013: 200-208.
|
| [11] |
GOLLAKOTA S, KATABI D. Physical layer wireless security made fast and channel independent[C]// Proceedings of IEEE INFOCOM. [S. l. ]: IEEE, 2011: 1125-1133.
|
| [12] |
HUANG P, WANG X. Fast secret key generation in static wireless networks: A virtual channel approach[C]// Proceedings of IEEE INFOCOM. [S. l]: IEEE, 2013: 2292-2300.
|
| [13] |
TUGNAIT J K, TONG L, DING Z. Single-user channel estimation and equalization[J].
IEEE journal of Signal Processing Magazine, 2000, 17(3): 16–28.
|
| [14] |
LIANG Y, POOR H V. Information theoretic security[J].
Foundations and Trends in Communications and Information Theory, 2009, 5(4-5): 355–580.
|
| [15] |
AHLSWEDE R, CSISZAR I. Common randomness in information theory and cryptography, part Ⅰ: Secret sharing[J].
IEEE Transactions on Information Theory, 1993, 39(4): 1121–1132.
|
| [16] |
ZENG K, WU D, CHAN A, et al. Exploiting multiple antenna diversity for shared secret key generation in wireless networks[C]//Proceedings of IEEE INFOCOM. [S. l. ]: IEEE, 2010: 1-9.
|
 2015, Vol. 44
2015, Vol. 44
