2. 电子科技大学数学科学学院 成都 611731;
3. 电子科技大学物理电子学院 成都 610054
2. School of Mathematical Sciences, University of Electronic Science and Technology of China Chengdu 611731;
3. School of Physical Electronics, University of Electronic Science and Technology of China Chengdu 610054
渗流是统计物理学和概率论中的基本概念之一,网络渗流一直被认为是非平衡相变的基础性模型[1]。文献[2]于1957年引入了渗流概念,用于描述流体在无序多孔介质中的流动行为。1959~1961年间,文献[3-4]提出了随机网络演化模型(ER模型):模型开始于
研究ER渗流模型的渗流过程具有重要的理论意义:其一,其相变过程可以通过数学方法得到论证,这就为用数学和统计物理方法研究自然界中广泛存在的相变现象提供了理论基础,对理解各种推广模型有着指导作用;其二,对真实系统来说,ER模型不可能都适合,但对它的研究可能成为研究复杂系统的切入点。同时,研究网络中最大分支尺度随边密度的变化规律也具有重要的实际意义:它可以作为解释很多真实系统连通性突变的理想模型,如多孔岩石[1]、电阻网络[5]、森林火灾[6],甚至社会网络[1, 7]等。特别地,如果把网络进化过程中的“添边连杆”考虑为传播疾病的接触方式,那么网络中最大连通分支的出现意味着该疾病疫情的传播[8]。因此,各种类型的随机图模型及其相变问题得到了广泛的研究[9-13]。研究的关键问题是:1)不同相变模型之间的关系;2)随机图模型相变的主要特征及其普适性问题。
2007年,文献[10]引进了一个很广泛的随机网络模型族。文中对模型族中的每个模型M,存在描述网络中最大分支的连续函数
Achlioptas过程是一个竞争过程[14],在该过程下可以构造许多竞争规则。这些规则又可分为有界尺度规则与无界尺度规则两大类。
有界尺度规则指连边选择仅仅依赖于两条候选边
文献[12]中提出的BF规则模型为典型的有界尺度规则。在BF规则模型中,开始于
对于无界尺度规则,则很难利用数学理论去解释,典型的无界尺度规则有PR乘积规则[14]和SR和规则,并且在两个规则下都可以得到“爆炸渗流”现象。在PR乘积规则中,系统开始于
 |
| 图1 PR规则下连边选择示意图[14] |
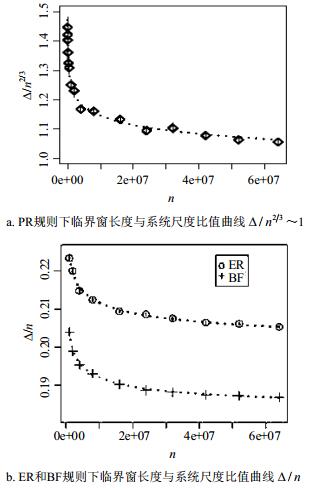 |
| 图2 不同加边规则下临界窗长度与系统尺度比值关系曲线[14] |
在爆炸渗流模型构建中,一些学者将连边的选取限制到具有共同顶点的边,这样候选边涉及3个及以上的分支,这类模型叫作局部分支聚集模型。文献[15]提出了两种局部分支聚集模型,即:邻接边模型(AE)和三角形规则模型(TR)。
AE是最简单的局部分支聚集模型,该规则仍然属于抑制大分支生长的模型,但其对大分支的抑制作用较SR和规则与PR乘积规则更弱。
局部分支聚集模型的优点在于可以用数学方程描述进化过程,也就是可以建立进化过程中的微分方程,并通过Euler方法对微分方程数值求解来粗略地获得相变点位置,这样的局部过程似乎可以为分析不连续渗流提供帮助。
文献[15]通过数值试验发现,AE规则下,对
在大量关于随机网络爆炸渗流研究展开的同时,无标度网络上的爆炸渗流也得到了广泛的关注[17-19]。文献[17-18]几乎同时研究了在网络结构高度异质的无标度网络上的渗流现象[19]。文献[17]研究了PR规则在无标度网络上的爆炸渗流,他们根据CL(Chung and Lu)模型[20]以及PR规则得到了控制参数为
文献[18]则用另一种规则构造了度分布指数为
前面提到的模型共同特点是在
在系统中随机选取一条边,如果接受它不会引起最大分支的生长或新的最大分支的形成,那么该边被添加到系统中;否则,该边被接受的概率
| ${q_1} = \min \left\{ {1,\exp \left[ { - \alpha {{\left( {\frac{{S - \bar S}}{{\bar S}}} \right)}^2}} \right]} \right\}$ | (1) |
式中,
文献[21]提出从系统中随机选出一条边,按照概率
| ${q_2} = \exp \left[ { - \alpha {{\left( {\frac{{S - \overline S }}{{\overline S }}} \right)}^2}} \right]$ | (2) |
接受该边。其中,
BFW模型是网络渗流研究中非常典型的模型之一,它由文献[22]在2004年提出。通过引入阶段数
| $g(k) = \alpha + {(2k)^{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}$ | (3) |
式中,
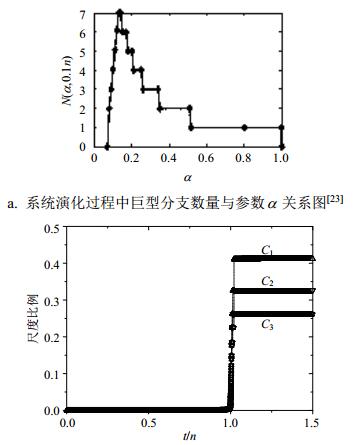 |
|
图3
不同参数 |
文献[24]又将筛边比例控制函数的收敛速度参数化,引进参数
| $g(k) = \frac{1}{2} + {(2k)^\beta }$ | (4) |
并且基于“临界窗”概念[14]和随机图渗流相变强弱不连续性与最大连通分支增长方式之间的关系[28],考察了参数
此外,文献[25]研究了BFW渗流模型在超临界区域内的渗流演化现象,并且发现存在参数临界点
BFW模型的巨大连通分支性质对研究网络模块结构的形成过程,网络结构探测[29]等方面均有重要的作用。此外,多重巨大连通分支的发现在疾病传播学、高分子聚合、通信网络等方面也有一定的应用前景[27]。
算法1 BFW模型算法
1) 初始化
系统
2) 添边过程
每次从系统中随机选取一条候选边
① 置
② 如果
③ 否则,如果
以上对于Achlioptas过程下的爆炸渗流模型及研究结果的介绍主要基于无穷维随机网络结构。同时,相关学者对有限维网络结构下的“爆炸渗流”也进行了大量的研究并取得了丰富的研究成果[21, 30-34, 36-38, 46, 65]。文献[31]首先将“乘积规则”引入到二维正方形网格的随机渗流模型中,同样得到了爆炸渗流现象;文献[35]对“乘积规则”的非局部效应与不连续相变的关系进行了研究;文献[37, 71]提出了广义Achlioptas过程,并给出了在广义连续渗流和不连续渗流相变参数区间。文献[38]等对二维和三维网格上的非限制性BFW模型以及高维(二维至七维)限制性BFW模型的渗流相变问题进行了深入的研究。
文献[39-41]重点关注和讨论了网络渗流中的三相点问题,三相点是指网络渗流变化过程中某个参数的变化导致渗流相变由不连续相变转换为连续相变的分界点,三相点问题的研究一直以来是统计物理学和数学领域有趣但又具有挑战性的问题之一。文献[39]提出了一个混合模型,通过调节控制参量来控制渗流相变类型,控制参量的变化使得渗流由“爆炸渗流”到经典渗流类型转换,并通过准确的数值模拟找到了非平衡三相点;文献[40]在ER模型和二维网格的“k-核”渗流里发现了三相点的存在性;另外,文献[41]也通过构造混合模型,并利用数值模拟和理论分析找到了经典渗流和爆炸渗流转换的三相点。
文献[42]通过扩展局域竞争机制提出了获取强不连续渗流模型,而且在系统进化过程中得到了多个稳定巨分支的共存现象。
而文献[43]将Achlioptas过程扩展到有向网络中,并研究了有向网络中的的爆炸渗流现象,得到PR乘积规则在有向网络中的渗流相变类型介于经典渗流类型和爆炸渗流之间,并称之为“弱爆炸渗流”。
文献[44-46]采用了不同的数值模拟方法对不同网络上的爆炸渗流现象进行了相应的研究,并指出爆炸渗流是一种奇异渗流,虽然序参量具有不连续特征,但是包括尺度分布在内的其他特征物理量却具有幂律标度行为[44],因此爆炸渗流相变既不是标准的不连续相变,又与常规随机渗流表现出的连续相变处于不同的普适类[45]。进一步,文献[46]指出:爆炸渗流相变其实为连续渗流相变。文献[47]研究了二维网格上乘积规则下的点渗流,并指出了其渗流相变为不连续的。文献[48]给出了AP规则下,爆炸渗流相变发生的必要条件。文献[50]在研究Achlioptas过程下的渗流相变过程中提出了“火药桶”的概念,并且指出,“火药桶”内的节点数在热力学极限下为
此外,文献[57]通过研究网络最大特征根在AP过程下的变化情况来研究信息或物质的传播效率,他们发现在具有爆炸渗流相变的演化过程下,信息或物质的传播效率明显降低。
2 爆炸渗流类型虽然Achlioptas过程下的随机网络渗流展现出“爆炸渗流”现象,并且其渗流相变类型也被认为是一阶相变,但是人们对其不连续性的验证主要停留在数值模拟上,而并没有建立严格的数学理论分析。然而Achlioptas过程下的随机图模型、二维网格模型、无标度网络模型及其他相似的爆炸性渗流模型下的序参量及其他特征物理量仍具有连续相变的幂律标度行为[15, 17-18, 21, 47-48],这与“爆炸渗流”的不连续相变结论相矛盾,从而引起了学者们对“爆炸渗流”相变到底是不连续的一阶相变还是连续的二阶相变问题的广泛的讨论与研究。
2010年,文献[58]指出“爆炸渗流”相变其实是连续的。其首先构造了一个的简单的渗流模型(CDGM模型),模型中,首先从系统中随机选择一对分支
文献[58]首先通过数值实验方法指出CDGM模型渗流变换符合连续相变特征,但是要说明渗流相变的连续性必须要在无限系统下经过严格的数学证明,文献[58]在无限系统下通过建立在
2011年,文献[59]指出爆炸渗流相变是连续的,但具有不寻常的有限尺度行为。通过使用有限尺度标度理论,对PR乘积规则,二维网格(2d),邻接边规则(AE)及CDGM规则的临界行为进行了广泛的数值实验和理论分析,并发现这4种规则下的渗流的确具有连续性,但它们每一个都处在不同的普适类中,并且均显示出不寻常的有限尺度行为,具有一个非解析的标度函数。
文献[60]进一步验证了乘积规则下的渗流相变为连续相变,但是随机图上的“爆炸渗流”相变连续性问题的研究和讨论仍然以数值模拟为主,理论分析具有相当的局限性或建立在较强的假设之上。
2011年,文献[61]解决了“爆炸渗流”相变连续性问题。尽管AP过程在一定系统规模下确实能够展示爆炸渗流,但该过程的确有连续的相变。文献[62]把渗流过程分成AP过程、混合l-顶点规则(ML)及一般的l-顶点规则(GL)3类。同时,考虑两种不同形式的连续性:首次连通性连续(fc)与全局连通性连续(gc)。通过较为严格的分析,得到上面3类过程均是fc连续的,同时,AP过程与ML规则还是gc连续的。文献[62]研究最终指出两点:1)任意一个基于选择一个固定数量的随机顶点的规则给出连续渗流变换;2)爆炸渗流是连续的。
一切竞争添边规则下的渗流相变都是连续的吗?文献[61]已经证明,对于3种类型的渗流过程,在相变点处展示的变换是连续的,且AP与ML过程是全局连续的。但是,他们没有对GL过程在相变点之后的情况说明什么。
2012年,文献[63]构造了一个所谓的推广三角形规则。通过广泛的数值实验和现象分析,得到的结论是:1)首次变换的连续性并不意味连续发散性的存在;2)极大连通集团可以通过多个小的连通集团来涌现,但多不连续跳跃仍然出现;3)序参量可以出现无限层次的不连续跳跃。推广的三角形规则为“竞争渗流总是连续的”论断提供了一个反例。
此外,文献[28]在研究不连续相变的微观机制的过程中提出了“强不连续”和“弱不连续”的概念。他们指出,在渗流演化过程中,由单条连边引起的最大连通分支尺度变化与系统尺度比值在热力学极限下为一非零常数,那么该渗流模相变为“强不连续”相变,否则为弱不连续相变,即
| $\mathop {\lim }\limits_{N \to \infty } \frac{{\Delta {C_{\max }}}}{N}>0$ | (5) |
则为“强不连续”相变。
由于随机网络只是欧式晶格上的平均场描述,而对于整个欧式空间上的“爆炸渗流”相变问题却没有一个统一的判定框架和理论基础,虽然对欧式空间上的EP问题已经有了相应的研究,并且数值结果表明其为不连续渗流[14],但是由于缺乏分析结果,欧式空间上的“爆炸渗流”相变阶数还不能确定。基于此,文献[64]引入了一个随机渗流模型,该模型中通过候选边竞争机制抑制连通分支之间的合并,并且通过启发式论点表明热力学极限下如果
为了进一步理解爆炸渗流性质对空间维数的依赖关系,在二维与三维网格上,文献[65]对在文献[34]中提出的6个不同模型的割边数(割点数)
文献[58]指出,爆炸渗流实际上是连续的,但是具有不寻常的渗流分支尺度分布的较小临界指数。文献[66]通过进一步的研究,提出了一个有效的基于分支尺度分布的进化方程的数值解,结合其幂律渐进的方法,发现了一系列典型爆炸渗流模型的相变是二阶相变的特征,且以较高的精度获得了每个模型的临界指数、振幅与临界点。
对于不同类型的代表性爆炸渗流模型,文献[67]提出了一个关于爆炸渗流相变的严格的标度理论,该理论提供了一系列完整的标度函数和临界指数。理论指出了与连续性问题相关的序参量与敏感度,解释了变换的连续性质和变换的不寻常特性。文献[72]则通过建立微分方程,并且寻找相应方程解的存在性来判定AP规则相变是否连续。
从目前情况看,关于爆炸渗流类型,有3种观点:1)爆炸渗流是非连续的,并且大多数学者是这样认为的;2)爆炸渗流是连续的,但具有不寻常的有限尺度行为;3)爆炸渗流是一种混合相变,既具有连续性特征,又具有许多不连续性特征,有着十分丰富的临界行为。值得指出的是在爆炸渗流是否连续性渗流的问题研究中,我国相关领域的学者[23-27, 38, 42-44, 68-71]也取得了重要的进展。
3 爆炸渗流的应用网络的爆炸渗流现象反映的是一种突发事件。突发事件在自然、科学和人类社会中是司空见惯的,在某些场合下需要创造条件使系统产生突变,而在另外的场合下又需要抑制突变。近几年来,有部分学者结合真实世界网络研究爆炸渗流,发现了Achlioptas渗流过程和一些真实网络进化过程十分类似,从而开启了网络爆炸渗流的应用研究。
2010年,文献[75]研究了人类蛋白质同源性网络拓扑(H-PHN)进化过程中的爆炸渗流现象,通过真实数据和同源蛋白质网络的生物学演化特征,首先在一定蛋白质规模上建模了网络,然后通过研究指出:蛋白质同源性网络的进化机制能够通过生长迟缓的分支来描述,也就是这些分支一直保持缓慢生长,直到过程的最后状态,当添加少量边时,会导致这些分支的迅速合并而产生巨型分支。所以他们指出,通过分叉复制事件而形成的H-PHN拓扑的进化过程可能发生在突然的几步中,这与在一阶相变中看到的情形一致。
2011年,文献[7]把爆炸渗流用于好几个真实网络的分析中。他们选择了移动电话网络(MPC),大型的论文合著网络(CA)和小型的论文合著网络(SCA)。通过研究,他们指出:1)当把爆炸渗流规则用到实证社会网络时,Achlioptas过程能够引起爆炸渗流变换;2)使用修改的最小化分支和规则(MC),即把连杆添加过程中的连杆比较数目设置为参数,如
文献[7]的研究实际上关注了两个问题:1)是否真实网络的拓扑特征在网络爆炸渗流中扮演了一个十分重要的角色?这些特征包括高聚集性、度相关性、社区结构和加权拓扑等;2)是否可以通过跟踪网络渗流过程本身,对网络结构认识带来一些重要信息?他们研究的结果得到了令人兴奋的结论。
从孤立系统出发,按照Achliopts过程下的某种添加边规则可以产生爆炸渗流,那么,一个真实系统由于受到随机失灵或恶意攻击后,系统中最大连通分支是否也会随着时间的变化而产生爆炸性突变呢?2010年,文献[79]以2003年9月28日发生在意大利电力网与信息网络间的级联失效为背景,对耦合基础设施的级联失效过程展开研究,提出了级联失效模型。借助于随机图度分布的母函数方法,提出了分析级联失效相变过程的数学框架,获取了相变点的解析计算方法。同时,如果两个耦合的网络均为随机图,在给出的耦合方式下,得到了相变渗流为爆炸渗流。类似于上面模型的方法,文献[80-81]提出了部分耦合的两个网络模型,得到两个依存网络间的耦合强度对相变类型产生重大影响,减小耦合强度,可以使渗流相变由一阶相变过度到联系相变。两个相互耦合的网络之间的边可以是依赖边也可以是连接边。一个更现实的两个耦合网络系统既有依赖边又有连接边。利用渗流理论,文献[82]发现了一个丰富和不寻常的混合相变现象,既有连续相变也有不连续相变。这种混合相变主要表现在系统首先出现了一级的跳变(不连续),随后又缓慢的变为零(连续)。文献[83-84]研究了相依边的长度及地理位置限制等对网络级联失效过程的影响,研究结果表明在某种条件下表现的更为脆弱。文献[85]研究给出了相互依赖网络级联失效过程中巨分支存在变化缓慢平台的原因。
4 回顾与展望本文对近年来国内外关于网络爆炸渗流的研究作了比较全面的综述。网络演化过程中的爆炸渗流现象是一惊人的发现。该发现丰富了传统的渗流理论,将为物理学、网络科学等的相变理论的研究提供新的视野、新的方法以及新的手段。同时,研究网络爆炸渗流现象,揭示其产生机理,发现其丰富的临界行为等又将对复杂网络控制、鲁棒性设计、动力学行为的研究等提供广阔的前景。
爆炸渗流的发现到研究虽然只有短短的几年,但却获得了许多不同凡响的成果,单在Science,Nature,PRL三大刊物上发表的相关论文就有数十篇。但是,爆炸渗流研究仍然面临许多挑战性工作[86-87],例如,1)目前采用的研究方法仍然以数值模拟为主,这必然受到规模效应的巨大约束,能否开发有效的爆炸渗流数学物理研究方法,将是一个长期的艰巨任务;2)爆炸渗流类型的争议目前仍然没有定论,到底爆炸渗流现象与传统的相变理论有何联系仍然值得进一步探索;3) Achlioptas过程下还会产生哪些奇特现象,这些现象对应什么样的真实物理过程,值得进一步探索;4)爆炸渗流与真实网络的联系研究还需要进一步深入,等等。
| [1] |
STAUFFER D, AHARONY A.
Introduction to percolation theory[M]. London: Taylor & Francis, 1994.
|
| [2] |
BROADBENT S R, HAMMERSLY J M. Percolation processes I. Crystals and Mazes[J].
Proceedings of the Cambridge Philosophical Society, 1957, 53(3): 629–641.
DOI:10.1017/S0305004100032680 |
| [3] |
ERDŐS P, RÉNYI A. On the evolution of random graphs[J].
Publ Math Inst Hungar Acad Sci, 1960, 5(1): 17–61.
|
| [4] |
ERDŐS P, RÉNYI A. On the evolution of random graphs II[J].
Bull Inst Int Stat, 1961, 38(4): 343–347.
|
| [5] |
DE ARCANGELIS L, REDNER L, CONIGLIO A. Anomalous voltage distribution of random resistor networks and a new model for the backbone at the percolation threshold[J].
Phys Rev B, 1985, 31(7): 4725–4727.
|
| [6] |
HENLEY C L. Statics of a "self-organized" percolation model[J].
Phys Rev Lett, 1993, 71(1): 2741–2744.
|
| [7] |
PAN R K, KIVELA M, SARAMAKI J, et al. Using explosive percolation in analysis of real-world networks[J].
Phys Rev E, 2011, 83(4): 046112.
DOI:10.1103/PhysRevE.83.046112 |
| [8] |
MOORE C, NEWMAN M E J. Epidemics and percolation in small-world networks[J].
Phys Rev E, 2000, 61(5): 5678–5682.
DOI:10.1103/PhysRevE.61.5678 |
| [9] |
GILBERT E N. Random graphs[J].
Ann Math Statist, 1959, 30(4): 1141–1144.
DOI:10.1214/aoms/1177706098 |
| [10] |
BOLLOBÁS B, JANSON S, RIORDAN O. The phase transition in inhomogeneous random graphs[J].
Random Structures & Algorithms, 2007, 31(1): 3–122.
|
| [11] |
YANG Y, WANG J H. Network observability transitions[J].
Phys Rev Lett, 2012, 109(25): 258701.
|
| [12] |
BOHMAN T, FRIEZE A. Avoiding a giant component[J].
Random Structures & Algorithms, 2001, 19(1): 75–85.
|
| [13] |
SPENCER J, WORMALD N. Birth control for giants[J].
Combinatorica, 2007, 27(5): 587–628.
|
| [14] |
ACHLIOPTAS D, D'SOUZA R M, SPENCER J. Explosive percolation in random networks[J].
Science, 2009, 323(5920): 1453–1555.
DOI:10.1126/science.1167782 |
| [15] |
D'SOUZA R M, MITZENMACHER M. Local cluster aggregation models of explosive percolation[J].
Phys Rev Lett, 2010, 104(19): 195702.
|
| [16] |
CHO Y S, KAHNG B, KIM D. Cluster aggregation model for discontinuous percolation transition[J].
Phys Rev E, 2010, 81(3): 030103.
DOI:10.1103/PhysRevE.81.030103 |
| [17] |
CHO Y S, KIM J S, PARK J, et al. Percolation transitions in scale-free networks under the Achlioptas process[J].
Phys Rev Lett, 2009, 103(13): 135702.
DOI:10.1103/PhysRevLett.103.135702 |
| [18] |
RADICCHI F, FORTUNATO S. Explosive percolation in scale-free networks[J].
Phys Rev Lett, 2009, 103(16): 168701.
DOI:10.1103/PhysRevLett.103.168701 |
| [19] |
GOMEZ-GARDENES J, GOMEZ S, ARENAS A, et al. Explosive synchronization transitions in scale-free networks[J].
Phys Rev Lett, 2011, 106(12): 128701.
DOI:10.1103/PhysRevLett.106.128701 |
| [20] |
CHUNG F, LU L. Connected components in random graphs with given expected degree sequences[J].
Annals of Combinatorics, 2002, 6(2): 125–145.
DOI:10.1007/PL00012580 |
| [21] |
ARAÚJO N A M, HERRMANN H J. Explosive percolation via control of the largest cluster[J].
Phys Rev Lett, 2010, 105(3): 035701.
DOI:10.1103/PhysRevLett.105.035701 |
| [22] |
BOHMAN T, FRIEZE A, WORMALD N C. Avoidance of a giant component in half the edge set of a random graph[J].
Random Structures and Algorithms, 2004, 25(4): 432–449.
DOI:10.1002/(ISSN)1098-2418 |
| [23] |
CHEN W, D'SOUZA R M. Explosive percolation with multiple giant components[J].
Phys Rev Lett, 2011, 106(11): 115701.
|
| [24] |
CHEN W, ZHENG Z, D'SOUZA R M. Deriving an underlying mechanism for discontinuous percolation[J].
EPL, 2012, 100(6): 66006.
DOI:10.1209/0295-5075/100/66006 |
| [25] |
CHEN W, NAGLER J, CHENG X, et al. Phase transitions in supercritical explosive percolation[J].
Phys Rev E, 2013, 87(5): 052130.
|
| [26] |
CHEN W, CHENG X Q, ZHENG Z M, et al. Unstable supercritical discontinuous percolation transitions[J].
Phys Rev E, 2013, 88(4): 042152.
DOI:10.1103/PhysRevE.88.042152 |
| [27] |
CHEN W.
Explosive percolation in random networks[M]. Berlin Heidelberg: Springer, 2014: 1-8.
|
| [28] |
NAGLER J, LEVINA A, TIMME M. Impact of single links in competitive percolation[J].
Nature Physics, 2011, 7(3): 265–270.
|
| [29] |
ASZTALOS A, TOROCZKAI Z. Network discovery by generalized random walks[J].
EPL, 2010, 92(5): 50008.
|
| [30] |
SCHRENK K J, ARAÚJO N A M, HERRMANN H J. Gaussian model of explosive percolation in three and higher dimensions[J].
Phys Rev E, 2011, 84(4): 041136.
|
| [31] |
ZIFF R M. Scaling behavior of explosive percolation on the square lattice[J].
Phys Rev E, 2010, 82(5): 051105.
|
| [32] |
CHAE H, YOOK S H, KIM Y. Explosive percolation on the Bethe lattice[J].
Phys Rev E, 2012, 85(5): 051118.
DOI:10.1103/PhysRevE.85.051118 |
| [33] |
CHOI W, YOOK S H, KIM Y. Bond-site duality and nature of the explosive-percolation phase transition on a two-dimensional lattice[J].
Phys Rev E, 2012, 86(5): 051126.
|
| [34] |
BASTAS N, KOSMIDIS K, ARGYRAKIS P. Explosive site percolation and finite-size hysteresis[J].
Phys Rev E, 2011, 84(6): 066112.
|
| [35] |
REIS S D S, MOREIRA A A, ANDRADE JR J S. Non-local product rules for percolation[J].
Phys Rev E, 2011, 85(4): 041112.
|
| [36] |
LONGONE P, CENTRES P M, RAMIREZ-PASTOR A J. Percolation of aligned rigid rods on two-dimensional square lattices[J].
Phys Rev E, 2012, 85(1): 011108.
DOI:10.1103/PhysRevE.85.011108 |
| [37] |
LIU M X, FAN J F, LI L S, et al. Continuous percolation phase transitions of two-dimensional lattice networks under a generalized Achlioptas process[J].
Eur Phys J B, 2012, 85(4): 132.
DOI:10.1140/epjb/e2012-20872-1 |
| [38] |
SCHRENK K J, FELDER A, DEFLORIN S, et al. Bohman-frieze-wormald model on the lattice, yielding a discontinuous percolation transition[J].
Phys Rev E, 2012, 85(3): 031103.
DOI:10.1103/PhysRevE.85.031103 |
| [39] |
ARAÚJO N A M, ANDRADE JR J S, ZIFF R M, et al. Tricritical point in explosive percolation[J].
Phys Rev Lett, 2011, 106(9): 095703.
|
| [40] |
CELLAI D, LAWLOR A, DAWSON K A, et al. Tricritical point in heterogeneous k-core percolation[J].
Phys Rev Lett, 2011, 107(17): 175703.
|
| [41] |
JIA X, HONG J S, YANG H C, et al. Characteristics of phase transitions via intervention in random networks[J].
Chin Phys B, 2014, 23(7): 076401.
|
| [42] |
HU J Q, YANG H C, YANG Y M. Two typical discontinuous transitions observed in generalized Achlioptas percolation process[J].
Chin Phys Lett, 2014, 31(7): 078901.
|
| [43] |
SQUIRES S, SYTWU K, ALCALA D, et al. Weakly explosive percolation in directed networks[J].
Phys Rev E, 2013, 87(5): 052127.
|
| [44] |
RADICCHI F, FORTUNATO S. Explosive percolation: A numerical analysis[J].
Phys Rev E, 2010, 81(3): 036110.
DOI:10.1103/PhysRevE.81.036110 |
| [45] |
LI Y, TANG G, SONG L J. Numerical simulations of the phase transition property of the explosive percolation model on Erdős-Rényi random network[J].
Acta Phys Sin, 2013, 62(4): 046401.
|
| [46] |
FORTUNATO S, RADICCHI F. Explosive percolation in graphs[C]//Journal of Physics: Conference Series. [S. l. ]: IOP, 2011, 297(1): 012009.
http://iopscience.iop.org/1742-6596/297/1/012009/ |
| [47] |
CHOI W, YOOK S H, KIM Y. Explosive site percolation with a product rule[J].
Phys Rev E, 2011, 84(2): 02010.
|
| [48] |
CHO Y S, KAHNG B. Suppression effect on explosive percolation[J].
Phys Rev Lett, 2011, 107(27): 275703.
DOI:10.1103/PhysRevLett.107.275703 |
| [49] |
MANNA S S, CHATTERJEE A. A new route to explosive percolation[J].
Physica A: Statistical Mechanics and its Applications, 2011, 390(2): 177–182.
DOI:10.1016/j.physa.2010.10.009 |
| [50] |
FRIEDMAN E J, LANDSBERG A S. Construction and analysis of random networks with explosive percolation[J].
Phys Rev Lett, 2009, 103(25): 255701.
|
| [51] |
MOREIRA A A, OLIVEIRA E A, REIS S D S, et al. Hamiltonian approach for explosive percolation[J].
Phys Rev E, 2010, 81(4): 040101.
|
| [52] |
LEE S B, KIM J S. Absorbing phase transitions in diluted conserved threshold transfer process[J].
Phys Rev E, 2013, 87(3): 032117.
|
| [53] |
LI J, OSTLING M. Corrected finite-size scaling in percolation[J].
Phys Rev E, 2012, 86(4): 040105.
|
| [54] |
ZIFF M. Getting the jump on explosive percolation[J].
Science, 2013, 339(6124): 1159–1160.
DOI:10.1126/science.1235032 |
| [55] |
RIORDAN O, WARNKE L. Achlioptas processes can be nonconvergent[EB/OL]. (2012-7-26). http://arxiv-web3.library.cornell.edu/abs/1111.6177v1.
|
| [56] |
HOOYBERGHS H, SCHAEYBROECK B V. Criterion for explosive percolation transitions on complex networks[J].
Phys Rev E, 2011, 83(3): 032101.
|
| [57] |
CHUNG N N, CHEW L Y, LAI C H. Spectral analysis on explosive percolation[J].
EPL, 2013, 101(6): 66003.
DOI:10.1209/0295-5075/101/66003 |
| [58] |
DA COSTA R A, DOROGOVTSEV S N, GOLTSEV A V, et al. Explosive percolation transition is actually continuous[J].
Phys Rev Lett, 2010, 105(25): 255701.
DOI:10.1103/PhysRevLett.105.255701 |
| [59] |
GRASSBERGER P, CHRISTERNSEN C, BIZHANI B, et al. Explosive percolation is continuous, but with unusual finite size behavior[J].
Phys Rev Lett, 2011, 106(22): 225701.
DOI:10.1103/PhysRevLett.106.225701 |
| [60] |
LEE H K, KIM B J, PARK H. Continuity of the explosive percolation transition[J].
Phys Rev E, 2011, 84(2): 020101.
|
| [61] |
RIORDAN O, WARNKE L. Explosive percolation is continuous[J].
Science, 2011, 333(6040): 322–324.
DOI:10.1126/science.1206241 |
| [62] |
RIORDAN O, WARNKE L. Achlioptas process phase transitions are continuous[J].
The Annals of Applied Probability, 2012, 22(4): 1450–1464.
DOI:10.1214/11-AAP798 |
| [63] |
NAGLER J, TIESSEN T, GUTCH H W. Continuous percolation with discontinuities[J].
Phys Rev X, 2012, 2(3): 031009.
|
| [64] |
CHO Y S, HWANG S, HERRMANN H J, et al. Avoiding a spanning cluster in percolation models[J].
Science, 2013, 339(6124): 1185–1187.
|
| [65] |
CHOI W, CHAE H, YOOK S H, et al. Dimensional dependence of phase transitions in explosive percolation[J].
Phys Rev E, 2014, 90(2): 022123.
|
| [66] |
DA COSTA R A, DOROGOVTSEV S N, GOLTSEV A V, et al. Critical exponents of the explosive percolation transition[J].
Phys Rev E, 2014, 89(4): 042148.
DOI:10.1103/PhysRevE.89.042148 |
| [67] |
DA COSTA R A, DOROGOVTSEV S N, GOLTSEV A V, et al. Solution of the explosive percolation quest: scaling functions and critical exponents[J].
Phys Rev E, 2014, 90(2): 022145.
DOI:10.1103/PhysRevE.90.022145 |
| [68] |
YANG Z, WEI W. Formation mechanism and size features of multiple giant clusters in generic percolation processes[J].
Phys Rev E, 2012, 86(5): 051103.
|
| [69] |
QIAN J H, HAN D D, MA Y G. Criticality and continuity of explosive site percolation in random networks[J].
EPL, 2012, 100(4): 48006.
DOI:10.1209/0295-5075/100/48006 |
| [70] |
TIAN L, SHI D N. The nature of explosive percolation phase transition[J].
Phys Lett A, 2012, 376(4): 286–289.
DOI:10.1016/j.physleta.2011.11.039 |
| [71] |
FAN J, LIU M, LI L, et al. Continuous percolation phase transitions of random networks under a generalized Achlioptas process[J].
Phys Rev E, 2012, 85(6): 061110.
DOI:10.1103/PhysRevE.85.061110 |
| [72] |
RIORDAN O, WARNKE L. Convergence of Achlioptas processes via differential equations with unique solutions [EB/OL]. (2013-6-27). http://arxiv.org/abs/1111.6179.
|
| [73] |
PANAGIOTOU K, SPÖHEL R, STEGER A, et al. Explosive percolation in Erdős-Rényi-like random graph processes[J].
Electronic Notes in Discrete Mathematics, 2011, 38(3): 699–704.
|
| [74] |
ANDRADE JR J S, HERRMANN H J, MOREIRA A A, et al. Transport on exploding percolation clusters[J].
Phys Rev E, 2011, 83(3): 031133.
DOI:10.1103/PhysRevE.83.031133 |
| [75] |
ROZENFELD H D, GALLOS L K, MAKSE H A. Explosive percolation in the human protein homology network[J].
Eur Phys J B, 2010, 75(3): 305–310.
|
| [76] |
BIZHANI G, PACZUSKI M, GRASSBERGER P. Discontinuous percolation transitions in epidemic processes, surface depinning in random media, and Hamiltonian random graphs[J].
Phys Rev E, 2012, 86(1): 011128.
DOI:10.1103/PhysRevE.86.011128 |
| [77] |
KIM Y, YUN Y, YOOK S H. Explosive percolation in a nanotube-based system[J].
Phys Rev E, 2010, 82(6): 061105.
|
| [78] |
JOVANOVIC B, BULDYREV S V, HAVLIN S, et al. Punctuated equilibrium and "history-dependent" percolation[J].
Phys Rev E, 1994, 50(4): 2403–2406.
|
| [79] |
BULDYREV S V, PARSHANI R, PAUL G, et al. Catastrophic cascade of failures in interdependent networks[J].
Nature, 2010, 464(7291): 1025–1028.
DOI:10.1038/nature08932 |
| [80] |
PARSHANI R, BULDYREV S V, HAVLIN S. Critical effect of dependency groups on the function of networks[J].
Proceedings of the National Academy of Sciences, 2011, 108(3): 1007–1010.
DOI:10.1073/pnas.1008404108 |
| [81] |
SON S W, GRASSBERGER P, PACZUSKI M. Percolation transitions are not always sharpened by making networks interdependent[J].
Phys Rev Lett, 2011, 107(19): 195702.
|
| [82] |
HU Y Q, KSHERIM B, COHEN R, et al. Percolation in interdependent and interconnected networks: abrupt change from second to first order transition[J].
Phys Rev E, 2011, 84(6): 066116.
DOI:10.1103/PhysRevE.84.066116 |
| [83] |
LI W, BASHAN A, BULDYREV S V, et al. Cascading failures in interdependent lattice networks: the critical role of the length of dependency links[J].
Phys Rev Lett, 2012, 108(22): 228702.
DOI:10.1103/PhysRevLett.108.228702 |
| [84] |
BASHAN A, BEREZIN Y, BULDYREV S V, et al. The extreme vulnerability of interdependent spatially embedded networks[J].
Nature Physics, 2013, 9(10): 667–672.
|
| [85] |
ZHOU D, BASHAN A, COHEN R, et al. Simultaneous first and second-order percolation transitions in interdependent networks[J].
Phys Rev E, 2014, 90(1): 012803.
DOI:10.1103/PhysRevE.90.012803 |
| [86] |
ARAÚJO N A M, GRASSBERGER P, KAHNG B, et al. Recent advances and open challenges in percolation[J].
The European Physical Journal Special Topics, 2014, 223(11): 2307–2321.
DOI:10.1140/epjst/e2014-02266-y |
| [87] |
BASTAS N, GIAZITZIDIS P, MARAGAKIS M, et al. Explosive percolation: unusual transitions of a simple model[J].
Physica A: Statistical Mechanics and its Applications, 2014, 407: 54–65.
DOI:10.1016/j.physa.2014.03.085 |
 2015, Vol. 44
2015, Vol. 44
