2. 河北联合大学基因组学与计算生物学中心 河北 唐山 063000
2. Center for Genomics and Computational Biology, Hebei United University Tangshan Hebei 063000
启动子通常定义为转录起始位点(transcription start site, TSS)上游邻近的功能区域。细菌的σ启动子分为两大家族,一类在进化上与大肠杆菌管家因子σ70相似,另一类在结构上与可变因子σ54同源。σ54因子能够形成关闭的启动子复合物,但不能自发进行转录,聚合酶依赖于另外的转录因子和附加的增强子结合蛋白来开始RNA合成[1]。许多不同的细菌使用依赖于σ54启动子的转录来控制许多环境响应进程,如趋化性传感器的表达和运动性器官的装配[2]。σ54启动子主要控制一些辅助的进程,包括甲苯和二甲苯的降解、二羧酸的输送、菌毛蛋白的合成、氮固定、氢摄取、鞭毛组装、精氨酸分解、藻蛋白酸盐生成、鼠李糖脂生成、乙偶姻分解、甘露糖摄取和脯氨酸亚氨基肽酶激活[3]。
σ70和σ54启动子具有丰富的序列多样性,σ70启动子在转录起始位点上游-10和-35位置均有保守区域[4],而σ54启动子的保守区域则分布在转录起始位点上游的-12和-24位置[3]。目前关于-12/-24区域的编译和分析是重要的研究方向,因此准确识别σ54启动子对研究并探索σ54启动子功能和调控有重要的作用。基于分子生物学实验的方法分析和鉴定启动子是进行启动子研究的主要途径。然而,实验方法费时、费钱,且效率低下。随着对启动子的序列特征以及结构功能的逐步认识,利用生物信息学方法,通过计算来预测基因启动子的相关信息获得越来越多的应用。
目前对于原核基因组中启动子的预测方法主要有隐马尔可夫模型(HMM)[5]、人工神经网络(ANN)[6]、支持向量机(SVM)[7]等算法。然而,这些算法主要应用于σ70启动子的预测,由于各大数据库中实验证实的σ54启动子序列较少,对σ54启动子的生物信息学研究尚处于起步阶段。
因此,本文在搜集足够的σ54启动子序列的基础上,对σ54启动子的序列位点保守性进行了分析,进而使用位置评分函数对该类启动子进行分类预测。Jackknife验证显示,基于位置打分函数的模型能够获得82.0%总体预测精度。该模型为进一步进行理论和实验研究σ54启动子提供帮助,位置权重矩阵也将会在更多关于生物序列的分析中得到运用。
1 材料与方法 1.1 数据库的建立大肠杆菌σ54启动子序列数据集来源于RegulonDB数据库[8]和文献[3],从RegulonDB中获取了92条σ54启动子序列,从文献[4]得到了76条σ54启动子序列,每条序列长81 bp(-60…+20,TSS作为0位置)。非启动子序列在大肠杆菌全基因组序列中的编码区和汇聚(convergent, CON)非编码区(两侧基因的转录末端位于该非编码区)选取[9]。为了避免正负集序列数目相差过大,本文随机选取84条编码区和84条CON非编码区序列作为非启动子数据集,每条序列长度也为81 bp。
1.2 保守性算法为了提取每段序列中最具有代表性的特征,本文计算任意一位点l处的保守性值为:
| $ {M_n}(l) = \sum\nolimits_i {{{[{p_i}(l) - 1/{4^n}]}^2}/(1/{4^n})} $ | (1) |
式中,n代表使用n联体进行保守性分析;pi(l)代表在位点l处第i种n联体片段出现的概率,对于n联体共有4n种片段。易证,保守性值Mn(l)服从卡方分布。
1.3 位置权重矩阵对于标准样本集,定义位置权重矩阵为P=(Pxl)M×L,其中M为n联体的种类数,L为序列的长度,Pxl代表某种n联体x在l位置出现的概率,即Pxl=nxl/N,N为样品集中序列的总数。然而在计算过程中,某种片段可能出现概率为0的情况,进而导致后续计算公式没有意义。因此在计算过程中引入了伪计数
| $ {p_{xi}} = ({n_{xi}} + {p_0}\sqrt N )/(N + \sqrt N ) $ | (2) |
式中,p0为背景频率,对于n联体,其背景频率为1/4n。
根据位置权重矩阵,定义位置关联评分函数为:
| $ {F_p} = \sum\nolimits_i^n {\ln ({p_{xi}}/{p_0})} $ | (3) |
不同的序列将对应不同的Fp值,因此用Fp值的大小来评估一条序列与标准样本集中启动子序列的相似程度,Fp值越大,则这条序列是启动子序列的可能性越高。
1.4 精确度评价本文使用下列参数来评价算法的预测性能:敏感性(Sn),特异性(Sp),准确度(ACC)。
| $ \rm{Sn = TP/(TP + FN)} $ | (4) |
| $ \rm{Sp = TN/(TN + FP)} $ | (5) |
| $ \rm{ACC = (TN + TN)/(TN + FN + TN + FP)} $ | (6) |
式中,TP代表正确预测的启动子数目;FP代表非启动子被预测为启动子的数目;FN代表启动子被预测为非启动子的数目;TN代表正确预测的非启动子数目。
2 结果与讨论利用Mn(l)对168条大肠杆菌的σ54启动子进行保守性分析,发现其保守位点与σ70启动子具有很大的差异。σ54启动子的保守位点在-24和-12区域,如图 1a所示。便于比较,σ70启动子的保守性曲线如图 1b所示。
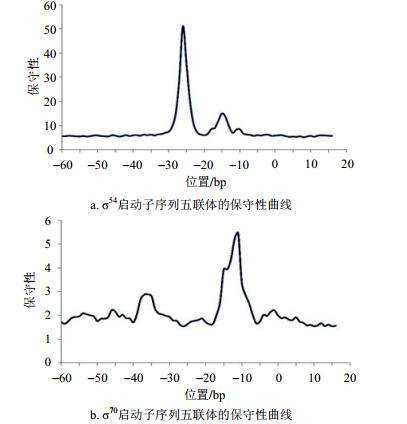 |
| 图1 五联体的曲线 |
图 1描述了五联体的保守性曲线。由图可以发现,σ54启动子两个主要峰值在-24区域和-12区域,而σ70启动子两个主要峰值在-35区域和-10区域。本文也研究了σ54启动子单碱基到4联体的保守性,发现随着从单体到五联体的变化,多联体的种类数也以指数形式增长,其Mn(l)~L曲线的光滑程度也逐渐增加,然而峰值的位置没有变。基于以上分析可知,图中描述的保守区域即为之前文献中报道的-24和-12区域[3]。
本文使用MEME[10]来分析大肠杆菌的σ54启动子的保守基序,获得的结果如图 2所示,其中横坐标代表启动子序列位点,纵坐标代表信息熵。正如先前文献报道的一样,在-24元件和-12元件周围找到了最保守的区域。在-24元件附近找到了5个高度保守的核苷酸,其序列为TGGCA。在-12元件附近同样找到了3个高度保守的核苷酸,其序列为TGC。另外还找到了一些保守性稍弱的核苷酸,综合的正则表达式为[CT]TGGCA[CT][GA][AGC][ACTG][TA] [CTA]TTGC[AT][TA]。
 |
| 图2 σ54启动子序列-24元件和-12元件的基序 |
通过对n联体的保守型分析,根据每个位点的Mn(l)值的大小为标准,选取特征位点,利用位置评分函数进行预测。首先,选取最大Mn(l)值的位点的n联体(n=1, 2, 3, 4, 5),以启动子和非启动子分别构建两个位置权重矩阵,使用Jackknife检验方法,对于每一条序列,分别利用两个位置权重矩阵对其打分,测试样本在哪一个矩阵中获得的分值较高,就属于哪一类别;其次,选取最大和次大Mn(l)值的位点,利用Jackknife检验进行模型精度评估;如此循环,直到所有位点都被选入,比较所有预测模型获得的预测精度,选择能够获得精度最高的位点的n联体作为构建最终预测模型的参数。联体n和位点数k两个参数需要调整。表 1列出了不同联体获得的最佳预测结果。
| 表1 位置评分函数对σ54启动子预测结果 |
由表 1可以看出,随着联体数目的增加,Sn有着明显的增加,而Sp先增加后减少。这种现象表明在不同联体预测过程中,敏感性的增加所付出的代价是特异性的降低。为了达到一个平衡状态,本文选取总体精度最高的三联体作为预测模型,17个最优位点分别为-31,-29,-28,-27,-26,-25,-24,-23,-22,-19,-16,-15,-14,-13,-12,-11,-10。该模型能够很好地平衡各个预测评价指标,使模型是最优的。
3 结束语本文通过使用位置权重矩阵对大肠杆菌σ54启动子进行了预测,根据结果显示,引入多联体和伪计数能够对启动子序列有更好的识别。碱基的短程关联是所有物种基因组的共性,特别是紧邻与次紧邻关联。本文使用三联体模式作为参数,不仅考虑了碱基的构成,还考虑了位置的关联特性。伪计数的引入是为了排除碱基频率计数时,由样本带来偏差所造成的影响,伪计数的大小与计数的标准偏差成正比。由于伪计数是一种根据先验概率对矩阵中每个位点碱基频率的估计,因此在矩阵中不会出现零,避免了求对数时可能会遇到的困难。使用Jackknife交叉检验对启动子预测算法进行评价,预测模型准确率和特异性都达到了80%。该模型的开发为进一步研究σ54启动子提供了理论工具。
| [1] |
MORETT E, SEGOVIA L. The sigma 54 bacterial enhancer-binding protein family: mechanism of action and phylogenetic relationship of their functional domains[J].
J Bacteriol, 1993, 175(19): 6067–6074.
DOI:10.1128/jb.175.19.6067-6074.1993 |
| [2] |
BERNARDO L M, JOHANSSON l, SKARFSTAD E, et al. Sigma54-promoter discrimination and regulation by ppGpp and DksA[J].
J Biol Chem, 2009, 284(2): 828–838.
DOI:10.1074/jbc.M807707200 |
| [3] |
BARRIOS H, VALDERRAMA B, MORETT E. Compilation and analysis of sigma(54)-dependent promoter sequences[J].
Nucleic Acids Res, 1999, 27(22): 4305–4313.
DOI:10.1093/nar/27.22.4305 |
| [4] |
LI Q Z, LIN H. The recognition and prediction of sigma70 promoters in Escherichia coli K-12[J].
J Theor Biol, 2006, 242(1): 135–141.
DOI:10.1016/j.jtbi.2006.02.007 |
| [5] |
LIN J C. Prediction of prokaryotic promoters based on prediction of transcriptional units[J].
Acta Biochim Biophys Sin, 2003, 35(4): 317–324.
|
| [6] |
DEMELER B, ZHOU G W. Neural network optimization for E coli promoter prediction[J].
Nucleic Acids Res, 1991, 19(7): 1593–1599.
DOI:10.1093/nar/19.7.1593 |
| [7] |
GORDON L, CHERVONENKIS A Y, GAMMERMAN A J, et al. Sequence alignment kernel for recognition of promoter regions[J].
Bioinformatics, 2003, 19(15): 1964–1971.
DOI:10.1093/bioinformatics/btg265 |
| [8] |
SALGADO H, PERALTA-GIL M, GAMA-CASTRO S, et al. RegulonDB v8.0: Omics data sets, evolutionary conservation, regulatory phrases, cross-validated gold standards and more[J].
Nucleic Acids Res, 2013, 41: D203–D213.
DOI:10.1093/nar/gks1201 |
| [9] |
BLATTNER F R, PLUNKETT G R D, BLOCH C A, et al. The complete genome sequence of escherichia coli K-12[J].
Science, 1997, 277: 1453–1462.
DOI:10.1126/science.277.5331.1453 |
| [10] |
BAILEY T L, ELKAN C. Fitting a mixture model by expectation maximization to discover motifs in biopolymers[J].
Proc Int Conf Intell Syst Mol Biol, 1994, 2: 28–36.
|
 2015, Vol. 44
2015, Vol. 44
