2. 中国科学院研究生院 北京 海淀区 100190
2. Graduate School, Chinese Academy of Sciences Haidian Beijing 100190
组织电阻抗(电导率)对反映病理和生理变化具有重要的临床价值,目前有多个国家竞相开展了电阻抗成像研究。国内外学者主要尝试通过两种途径发展电阻抗成像:1)利用其功能分辨率的临床潜在优势将电阻抗成像推向实用,研究利用电阻抗进行监护的方法[1];2)研究与超声、核磁共振等相结合的混合成像方法,解决空间分辨率不高的问题[2-3]。磁声成像方法(MAT)[4-6]和磁声电成像(MAET)[7-9]是两种典型的电阻抗成像和超声相结合的成像方法,融合了电阻抗成像技术和超声扫描成像技术,兼具无创、对比度好、灵敏度高以及空间分辨率高等优点。MAT和MAET两种成像方法互为反模式,MAT利用注入电流(或感应电流)和静磁场激励生物组织产生洛伦兹力振动形成超声波,提取超声信号重建成像体的电导率分布;MAET利用超声波和静磁场产生洛伦兹力,激励生物组织检测电信号重构电阻抗图像。从电工学角度可见,MAT依据的是电动机原理,而MAET依据的则是发电机原理。相比MAET,MAT在国际上是前沿和热点研究方向,研究人员在数学物理模型[10-11]、声电激励与信号转换实验[12]、信息检测与图象重建方法[13]等方面开展了相应的研究工作。
MAET可以看成MAT的反模式,该方法起步较晚,它的具体原理是将一束超声波注入成像体,成像体中的局部离子随超声波的传播而振动,振动的离子在静磁场作用下受到洛伦兹力作用而引起电荷分离,在成像体内形成局部电场,通过贴放在成像体上的接收电极或与成像体非接触的接收线圈检测电信号重构电阻抗图像。MAET作为一种新型的电阻抗成像与超声成像相结合的技术,与传统的电阻抗成像技术相比,具有4方面的优点。
1) 激励方面。磁声电成像采用超声探头遍历置于静磁场中的被测目标体。不同于传统电阻抗的整区激励方式,借助互易定理,利用超声离子振动速度和静磁场信息,分区获取电流密度;而传统的成像方法则是在重建过程中才对目标体进行区域分解,利用的是整体电流密度信息。
2) 测量方面。理论上将仅采用一对接收电极即可实现空间分布区域的电导率重建,这是传统电阻抗成像方法无法做到的。
3) 图像重建方面。磁声电成像方法理论上可以采用超声声速编码技术,精确获取目标体的空间信息,采用超声聚焦技术可以有效地控制图像横向分辨率。
4) 多场耦合方面。磁声电成像采用超声激励与磁场耦合产生的电场作为激励源,结合了电磁探测对比度高和超声成像分辨率高的优点,便于与传统超声成像技术联合使用,有利于信息互补,做出更准确的诊断。
综上所述,磁声电成像是一种有望获得高质量图像的生物电磁成像方法。目前国内外对磁声电的研究还处于起步阶段,尚没有完善的理论模型和系统实验。本文在基于互易定理的理论研究基础上,实现二维模型电流密度和电导率分布的重建图像,同时对超声探头焦斑大小和扫描步长对重建图像质量的影响进行分析。
1 电磁场正逆问题分析 1.1 电磁场正问题研究设电极在成像体a、b处测得的MAET电压差为
| $ {U_{ab}} = \int_V {{\mathit{\boldsymbol{J}}_{ab}} \cdot (\mathit{\boldsymbol{v}} \times {\mathit{\boldsymbol{B}}_0}){\rm{d}}V} $ | (1) |
利用式(1)获得了测量电极a、b处检测到的MAET表面电压信号的定量求解公式。
如式(1)所示,MAET电磁场正问题可以分为两组:1)已知局部电场源为
第一组正问题的几何模型如图 1所示,为厚度可忽略的二维成像体,置于静磁场
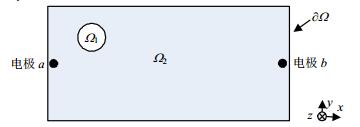 |
| 图1 二维成像体示意图 |
局部电场源激发的电场为库仑电场,感应电场非常小可忽略,采用电准静态近似,并引入标量电位
| $ \nabla \cdot (\sigma \nabla u) = \nabla \cdot (\sigma \mathit{\boldsymbol{v}} \times {\mathit{\boldsymbol{B}}_0}) $ | (2) |
在局部电场源外的区域中(记为
| $ \nabla \cdot (\sigma \nabla u) = 0 $ | (3) |
边界条件为:
| $ {\left. {\sigma \frac{{\partial u}}{{\partial n}}} \right|_{\partial \mathit{\Omega} }} = 0 $ | (4) |
由式(2)~式(4)通过数值求解,可以计算出成像体内的电压分布,进一步可计算出电极a、b的电势差
| $ \nabla \cdot (\sigma \nabla u) = \delta (\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{r}}_a}) - \delta (\mathit{\boldsymbol{r}} - {\mathit{\boldsymbol{r}}_b}) $ | (5) |
式中,
边界条件为:
| $ \sigma {\left. {\frac{{\partial u}}{{\partial n}}} \right|_{\partial \mathit{\Omega} }} = 0 $ | (6) |
式(5)和式(6)即为单位电流注入成像体所满足的电磁场边值问题。
1.2 电磁场逆问题研究由式(1)可以看出,MAET重建可以分为两个步骤:1)重建电流密度
| $ {\left. {{{\bar J}_{ab}}} \right|_x} = \frac{{{U_{ab}}}}{{\bar v{B_0}ds}} $ | (7) |
式中,
| $ \begin{array}{l} Q(\mathit{\boldsymbol{\sigma }}) = \sum\limits_{i = 1}^n {\int_{{\mathit{\Omega} _\iota }} {{{\left| {{\mathit{\boldsymbol{J}}^M}(\mathit{\boldsymbol{r}}) - \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{r}})} \right|}^2}} } {\rm{d}}\mathit{\Omega} \\ = \sum\limits_{i = 1}^n {\int_{{\mathit{\Omega} _\iota }} {{{\left| {{\mathit{\boldsymbol{J}}^M}(\mathit{\boldsymbol{r}}) + {\sigma _i}\nabla \mathit{\boldsymbol{U}}} \right|}^2}} {\rm{d}}\mathit{\Omega} } \end{array} $ | (8) |
式中,
| $ \begin{array}{l} Q(\mathit{\boldsymbol{\sigma }}) = \sum\limits_{i = 1}^n {\int_{{\mathit{\Omega} _i}} {({\mathit{\boldsymbol{J}}^M}(\mathit{\boldsymbol{r}}) + {\sigma _i}\nabla \mathit{\boldsymbol{U}}) \cdot ({\mathit{\boldsymbol{J}}^M}(\mathit{\boldsymbol{r}}) + {\sigma _i}\nabla \mathit{\boldsymbol{U}})} } {\rm{ d}}\mathit{\mathit{\Omega} } \\ = \sum\limits_{i = 1}^n {\int_{{\mathit{\Omega} _i}} {({\mathit{\boldsymbol{J}}^M} \cdot {\mathit{\boldsymbol{J}}^M} + 2{\sigma _i}{\mathit{\boldsymbol{J}}^M} \cdot \nabla \mathit{\boldsymbol{U}} + \sigma _i^2\nabla \mathit{\boldsymbol{U}} \cdot \nabla \mathit{\boldsymbol{U}})} } {\rm{d}}\mathit{\mathit{\Omega} } \end{array} $ | (9) |
采用最小二乘法对式(9)的目标函数极小化,有:
| $ \begin{array}{l} \frac{{\partial Q(\sigma )}}{{\partial {\sigma _i}}} = 2\int_{{\mathit{\Omega} _i}} {({\mathit{\boldsymbol{J}}^M} \cdot \nabla \mathit{\boldsymbol{U}} + {\sigma _i}\nabla \mathit{\boldsymbol{U}} \cdot \nabla \mathit{\boldsymbol{U}})} {\rm{d}}\mathit{\Omega} = 0\\ i = 1,2, \cdots ,n \end{array} $ | (10) |
因此有:
| $ {\sigma _i} = \frac{{ - \int_{{\mathit{\Omega} _i}} {{\mathit{\boldsymbol{J}}^M} \cdot \nabla \mathit{\boldsymbol{U}}} {\rm{ d}}\mathit{\Omega} }}{{\int_{{\mathit{\Omega} _i}} {\nabla \mathit{\boldsymbol{U}} \cdot \nabla \mathit{\boldsymbol{U}}} {\rm{ }}2{\rm{d}}\mathit{\Omega} }}\;\;\;\;i = 1,2, \cdots ,n $ | (11) |
给定样品初始电导率,通过重复迭代,便可以达到预先给定的精度值,求出电导率分布。
2 电流密度和电导率重建首先验证电流密度重建和电导率重建的可行性,设计铜片扫描实验,铜片几何尺寸如图 2所示,尺寸为6 cm×10 cm×1 mm,中间两侧切除的部分尺寸为2 cm×3 cm。
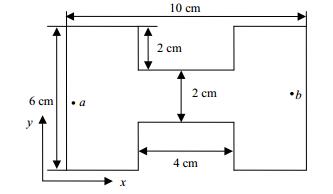 |
| 图2 重建仿真几何模型 |
通过图 2所述模型,根据式(7)可以计算出各扫描区域内电流密度分布的
 |
| 图3 重建的电导率分布图 |
在验证了重建算法的基础上,建立如图 4所示的几何模型,其几何尺寸如图 4所示。设背景区域
首先设扫描步径为
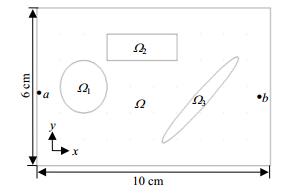 |
| 图4 重建几何模型 |
 |
| 图5 重建的电流密度和电导率分布图 |
图 5a、图 5b和图 5c所示分别为重建的
为了论证焦斑大小对图像分辨力的影响,仍采用图 4所示模型,扫描步径设为
 |
| 图6 焦斑大小不同时重建结果细节图 |
 |
| 图7 扫描路径不同时重建出来的图像细节图 |
不改变焦斑大小,改变扫描步径,考查扫描步径对重建图像质量的影响。设焦斑直径为
在基于互易定理的理论研究基础上,本文实现二维模型电流密度分布的重建图像和电导率的图像重建。同时对超声探头焦斑大小和扫描步长对重建图像质量的影响进行定性的分析。综合以上的仿真结果,重建的电流密度图像和电导率图像较好地显示了被测样本形状,区别出不同的电导率。由以上的仿真实验可以得出:1)通过本文的仿真方法,重建图像理论上的横向分辨率由超声探头的焦斑大小决定,焦斑越小横向分辨率越高;纵向分辨率也可以成为轴向分辨率由超声脉冲宽度和超声波在样本中的声波传输速度的乘积决定。2)扫描步径减小,即扫描次数增多,有助于改善成像质量;但当扫描步径小到一定程度后,对图像质量的影响不再明显。
| [1] |
董秀珍. 生物电阻抗成像研究的现状与挑战[J].
中国生物医学工程学报, 2008, 27(5): 641–649.
DONG Xiu-zhen. Recent progress and challenges in the study of bio-impedance imaging[J]. Chinese Jonrnal of Biomedical Engineering, 2008, 27(5): 641–649. |
| [2] |
ROTH B J, BASSER P J, WIKSWO J P. A theoretical model for magneto-acoustic imaging of bioelectric currents[J].
IEEE Transactions on Biomedical Engineering, 1994, 41(8): 723–728.
DOI:10.1109/TBME.1994.6492304 |
| [3] |
XU Y, HE B. Magnetoacoustic tomography with magnetic induction(MAT-MI)[J].
Physics in Medicine and Biology, 2005, 50: 5175–5187.
DOI:10.1088/0031-9155/50/21/015 |
| [4] |
HAIDER S, HRBER A, XU Y. Magneto-acousto-electrical tomography: a potential method for imaging current density and electrical impedance[J].
Physiological Measurement, 2008, 29(6): 41–50.
DOI:10.1088/0967-3334/29/6/S04 |
| [5] |
RENZHIGLOVA E, IVANTSIV V, XU Y. Difference frequency magneto-acousto-electrical tomography (DF- MAET): Application of ultrasound-induced radiation force to imaging electrical current density[J].
IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57(11): 2391–2402.
DOI:10.1109/TUFFC.2010.1707 |
| [6] |
LIU Guo-qiang, WANG Hao. Reconstruction method of magnetoacoustic tomography with magnetic induction (MAT-MI)[C]//IFMBE Proceedings. Berlin, Heidelbeg: Springer, 2007.
|
| [7] |
LIU Guo-qiang, HUANGN Xin, XIA Hui. Magnetoacoustic tomography with applied current[J].
Chinese Science Bulletin, 2013, 58(30): 3600–3606.
DOI:10.1007/s11434-013-5964-2 |
| [8] |
XU Y, HAIDER S. Magneto-acousto-electrical tomography: a new imaging modality for electrical impedance[C]// IFMBE Proceedings. Berlin, Heidelbeg: Springer, 2007, 17: 292-295.
|
| [9] |
夏慧, 刘国强, 黄欣, 等. 基于互易定理的二维磁声电成像系统[J].
电工技术学报, 2013, 28(7): 163–168.
XIA Hui, LIU Guo-qiang, Huang Xin, et al. 2D magneto -acousto-electrical tomography system based on reciprocity theorem[J]. Transactions of China Electrotechnical Society, 2013, 28(7): 163–168. |
| [10] |
XIA Hui, LIU Guo-qiang. Experimental study of Magneto-acousto-electrical tomography[C]//2011 2nd International Conference on Mechanic Automation and Control Engineering. Hohhot: IEEE, 2011.
|
| [11] |
XIA R M, LI X. Reconstruction of vectorial acoustic sources in time-domain tomography[J].
IEEE Transactions on Medical Imaging, 2009, 28(5): 669–675.
DOI:10.1109/TMI.2008.2008972 |
| [12] |
黄欣, 刘国强, 夏慧. 感应式磁声成像的脉冲磁场研究[J].
电工技术学报, 2013, 28(2): 67–72.
HUANG Xin, LIU Guo-qiang, XIA Hui. Study of plused magnetic field used in magnetioacoustic tomography with magnetic induction[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 67–72. |
| [13] |
ZENG X P, LIU G Q, XIA H, et al. Steady state electromagnetic analysis of the forward problem for Magneto-acoustic tomography[C]//The 2nd International Conference on Information Science and Engineering. Hangzhou, China: IEEE, 2010.
|
| [14] |
刘国强.
医学电磁成像[M]. 北京: 科学出版社, 2006.
LIU Guo-qiang. Medical electromagnetic imaging[M]. Bei jing: Science Press, 2006. |
 2015, Vol. 44
2015, Vol. 44
