2. 江苏物联网研究发展中心 江苏 无锡 214135
2. Jiangsu R & D Center for Internet of Things Wuxi Jiangsu 214135
遥感图像融合是图像融合的一个重要分支,针对全色光图像与多光谱图像的融合始终是遥感图像处理领域的研究热点。随着传感器技术的飞速发展,许多在轨卫星,如SPOT、IKONOS、QuickBird等能够同时提供高分辨率全色光图像与多光谱图像。通常,多光谱图像包含多个波段,具有较高的光谱分辨率,但其空间分辨率相比于单波段全色光图像较低。图像融合技术就是利用高分辨率全色光图像去提高多光谱图像的空间分辨率。通过融合得到的具有高空间分辨率的多光谱图像可用于诸如谷歌地球、城市规划、高精度地物分类等众多领域。
新型WorldView-2(WV-2)星载图像代表了下一代超高分辨率遥感图像的发展趋势,同时也对现有的图像融合方法提出了挑战[1-2]。为了突破输入波段数量的限制,文献[3]提出了一种基于超球面彩色变换(hyperspherical color sharpening, HCS)的融合方法,将WV-2所有8波段多光谱数据一次性地从原始空间转换到超球面彩色空间进行处理。尽管该方法已成为ERDAS IMAGINE 2011商业软件的模块,但是其融合结果仍会出现明显的光谱失真。文献[4]提出一种带有可调参数(adjustable pan-sharpening, APS)的图像融合方法,以处理包含WV-2在内的多种高分辨率遥感图像。APS方法通过分析不同星载传感器强度分量匹配关系,利用两个可调参数整合了传统的色度-强度-保和度(intensity-hue-saturation, HIS)、Bravery变换(Bravery transform, BT)以及光滑调制滤波(smoothing-filter-based intensity modulation, SFIM)融合方法,实现了在5种融合模式中的切换。文献[5]利用WV-2多光谱数据地物分类的先验信息设计了一种基于广义HIS(generalized HIS, GIHS)变换的融合方法,然而地物分类精度对融合质量的影响并未展开讨论。
本文针对WV-2传感器各波段的光谱响应特点,提出了一种基于对应分析的融合新方法。利用多光谱和全色光波段间的相对光谱响应关系构造出合适的低分辨率全色光图像,进而提取出原始全色光图像的空间细节信息,并注入至对应分析变换的成分空间中,最终得到高质量的融合结果。
1 WorldView-2遥感图像2009年10月8日发射升空的WV-2卫星能够同时提供8波段多光谱图像(Band1=Coastal、Band2= Blue、Band3=Green、Band4=Yellow、Band5=Red、Band6=RedEdge、Band7=NIR1、Band8=NIR2)和单波段全色光图像(panchromatic,PAN)。多光谱传感器的光谱覆盖范围为400~1 050 nm,空间分辨率为1.84 m;全色光传感器光谱范围为450~800 nm,空间分辨率为0.46 m。其相对光谱响应如图 1所示。
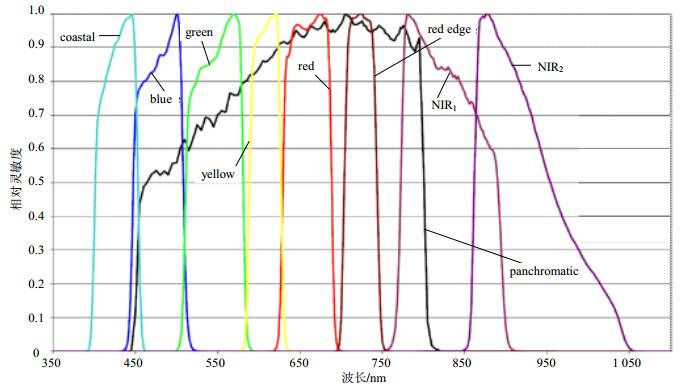 |
| 图1 WV-2传感器相对光谱响应 |
与QuickBird、IKONOS、GeoEye-1等高分辨率遥感图像相比较:1) WV-2数据包含的多光谱波段划分更细、通道数更多;2)全色光波段的光谱覆盖范围变窄;3)多光谱与全色光波段光谱响应之间的匹配发生了明显的变化,特别是Band1和Band8基本上在PAN波段光谱响应之外。正是这些新特点给遥感图像融合研究带来了新的挑战,现有的许多融合方法并不适合于WV-2遥感图像,若直接套用,则会出现严重的光谱和空间信息失真现象。
2 对应分析变换对应分析(correspondence analysis, CA)是近年来发展起来的一种多元相依变量统计分析技术,通过分析由定性变量构成的数据列联表来揭示同一变量的各个类别之间的差异,以及不同变量各个类别之间的对应关系。若数据列联表中的元素是同源的且非负,那么也可以用对应分析方法对其分析[6]。针对多光谱遥感图像,可以利用
首先,将列联表中每个元素
| ${x_{ij}} = \sqrt {{x_{ + + }}} \frac{{{p_{ij}} - {p_{i + }}{p_{ + j}}}}{{\sqrt {{p_{i + }}{p_{ + j}}} }}$ | (1) |
若使用
| $\mathit{\boldsymbol{Q}} = [{q_{ij}}] = \left[ {\frac{{{p_{ij}} - {p_{i + }}{p_{ + j}}}}{{\sqrt {{p_{i + }}{p_{ + j}}} }}} \right]$ | (2) |
其特征向量矩阵为:
| $\mathit{\boldsymbol{U}} = {\mathit{\boldsymbol{Q}}^{\bf{T}}}\mathit{\boldsymbol{Q}}$ | (3) |
这样,利用特征向量矩阵
| ${\mathit{\boldsymbol{Y}}} = {{\mathit{\boldsymbol{U}}}^\bf{T}}{\mathit{\boldsymbol{X}}}$ | (4) |
其反变换为:
| ${\mathit{\boldsymbol{X}}} = {({{\mathit{\boldsymbol{U}}}^\bf{T}})^{ - 1}}{\mathit{\boldsymbol{Y}}}$ | (5) |
一个好的融合方法在提高多光谱图像空间分辨率的同时,还应该尽可能地保持多光谱图像的原始光谱信息。本文针对WV-2遥感图像提出了一种基于对应分析的融合方法,将输入波段数扩展至任意多个,其融合框架如图 2所示。
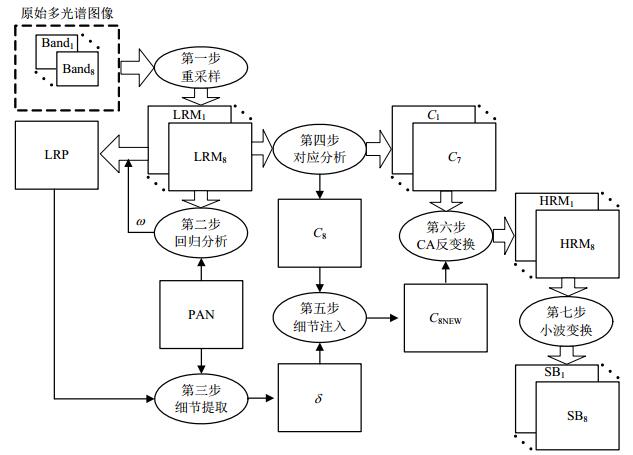 |
| 图2 融合框架图 |
由图 2可知,该融合方法分以下7步实施。
1) 将8波段多光谱图像(Band1, Band2,
2) 利用多元线性回归方法预测多光谱图像与全色光图像间的关系。理论上可以假设全色光图像PAN与高分辨率多光谱图像HRM满足线性关系,即
考虑到WV-2数据中全色光图像与多光谱图像的Band 1和Band 8的光谱响应几乎没有重叠(如图 1所示),因此本文只选择LRM2, LRM3,
| ${\rm PAN} = \sum\limits_{i = 2}^7 {{\omega _i}{\rm LR}{{\rm M}_i}} + b$ | (6) |
3) 全色光图像的空间细节提取。利用式(6)计算得到的权系数ωi及偏置b可进一步构造出低分辨率的全色光图像,即:
| ${\rm LRP} = \sum\limits_{i = 2}^7 {{\omega _i}{\rm LR}{{\rm M}_i}} + b$ | (7) |
构造出的LRP与LRM在空间分辨率上是相同的,可以通过原始全色光图像与构造出的低分辨率全色光图像的比值来获取空间细节信息,即:
| $\delta = {\rm PAN}/{\rm LRP}$ | (8) |
4) 光谱图像的对应分析变换。利用重采样的多光谱数据构造输入矩阵:
| ${\mathit{\boldsymbol{X}}_{{{\rm IN}}}} = [{\rm LR}{{\rm M}_{\rm 1}},{\rm LR}{{\rm M}_{\rm 2}}, \cdots ,{\rm LR}{{\rm M}_{\rm 8}}]$ | (9) |
按照对应分析变换式(1)~式(4)将输入矩阵XIN变换到成分空间,得到成分空间[C1, C2,
5) 空间细节的注入。由于空间细节图像
| ${C_8}_{{{\rm NEW}}} = \delta {C_{\rm 8}}$ | (10) |
6) CA反变换。用C8NEW替换C8,再按照式(5)对新成分空间[C1, C2,
7) 小波变换。重采样多光谱图像由于采用最近邻插值会产生方块或锯齿效应,特别是在轮廓和边缘部分较为明显,因此可以引入冗余小波变换方法去除步骤6)得到的高分辨率多光谱图像(HRM1, HRM2,
WV-2实验数据集包含空间分辨率为2.0 m的8波段多光谱图像和0.5 m的全色光图像,原始尺寸1600×1600像素,场景是2011年4月拍摄的澳大利亚悉尼港区域,其RGB彩色合成图像(Band 5-3-2)如图 3所示。多光谱图像与全色光图像已经过配准。为了验证本文方法的有效性和先进性,先后与文献[4]的APS方法、文献[3]的HCS方法以及文献[8]的IAWP方法的实验结果进行对比,并采用相关系数(correlation coefficient, CC)、空间相关系数(spatial CC, SCC)、相对全局维数综合误差(relative global dimensional synthesis error, ERGAS)以及光谱角映射(spectral angle mapper, SAM)4种常用客观评价指标对各方法的融合结果进行客观评价[9-12]。为方便显示,图 4给出了400×400像素的子场景。融合实验的硬件环境为Intel CPU 3.10 GHz,4 GB内存,64 bit Windows 7操作系统;编程环境为ENVI 4.1/IDL 6.1。
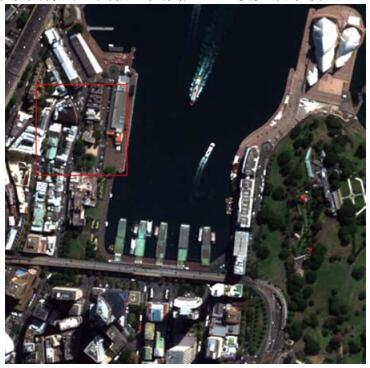 |
| 图3 原始多光谱RGB图像 |
 |
| 图4 400×400像素子场景及其融合结果 |
由图 4可知,该子场景包含地物内容较丰富,有植被、建筑物、车辆、道路等。4种方法的融合结果与原始多光谱图像(图 4a)相比,其空间分辨率均有不同程度地提高。本文方法与APS方法在空间分辨率提升方面效果显著,图像的清晰程度基本能与全色光图像(图 4b)保持一致。但APS方法在光谱保持方面却略显不足,特别是在绿色植被区域将原有的深绿色扭曲为浅黄绿色,出现了色彩失真。
HCS方法的空间分辨率提高不够,并且在高亮度的白色屋顶部分出现了明显的光谱失真。IAWP方法尽管其光谱保持能力较强,但细节信息注入不够,导致图像的空间信息失真严重,视觉效果较差。
4种融合方法的客观评价结果如表 1所示。从表中可以看出,IAWP方法的CC数值说明其光谱保持能力强,但是SCC评价最差说明其空间分辨率增强效果最差。APS方法的SCC评价最高,但是其ERGAS、SAM和CC数值说明该方法的光谱保持能力以及总体质量不是最优。本文方法在ERGAS和SAM数值优势明显,SCC评价非常接近APS方法,说明本文方法在空间分辨率提高和光谱信息保持方面达到了更好的平衡,融合结果的整体质量最好,主观评价与客观分析结果能够达到一致。
| 表1 4种融合方法的客观评价结果 |
针对新型高分辨率WorldView-2遥感图像,本文从传感器各波段光谱响应特点入手,有选择性地利用多光谱图像构造低分辨率全色光图像,进一步提取出原始全色光图像的空间信息并将其注入至多光谱图像的成分空间中,经对应分析反变换,再利用冗余小波变换去除各波段的块效应得到最终融合结果。融合实验对几种方法进行验证,实验结果的主观评价和客观分析表明,本文提出的新方法相比于其他几种融合方法在提高空间分辨率和保持光谱信息方面能够达到更好的平衡。
| [1] |
AGUILAR M A, SALDANA M M, AGUILAR F J. GeoEye-1 and WorldView-2 pansharpened imagery for object-back classification in urban environments[J].
International Journal of Remote Sensing, 2013, 34(7): 2583–2606.
DOI:10.1080/01431161.2012.747018 |
| [2] |
LONGBOTHAM N, CHAAPEL C, BLEILER L, et al. Very high resolution multiangle urban classification analysis[J].
IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1155–1170.
DOI:10.1109/TGRS.2011.2165548 |
| [3] |
PADWICK C, DESKEVICH M, PACIFICI F, et al. WorldView-2 pan-sharpening[C]//Proceedings of the Annual Conference on ASPRS. San Diego, California: [s. n. ], 2010.
http://www.mendeley.com/catalog/worldview2-pansharpening/ |
| [4] |
TU T, HSU C, TU P, et al. An adjustable pan-sharpening approach for IKONOS/QuickBird/GeoEye-1/WorldView-2 imagery[J].
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2012, 5(1): 125–134.
DOI:10.1109/JSTARS.2011.2181827 |
| [5] |
JI M, CHEN W, WANG W. Improving spectral fidelity of WorldView-2 image fusion via a constrained generalized intensity-hue-saturation model with localized weight structure through land cover classification[J].
Journal of Applied Remote Sensing, 2012, 6(1): 123–129.
|
| [6] |
CAKIR H I, KHORRAM S, NELSON S. Correspondence analysis for detection land cover change[J].
Remote Sensing of Environment, 2006, 102(3): 306–317.
|
| [7] |
LI X, HE M Y, ROUX M. Multifocus image fusion based on redundant wavelet transform[J].
IET Image Processing, 2010, 4(4): 283–293.
DOI:10.1049/iet-ipr.2008.0259 |
| [8] |
KIM Y, LEE C, HAN D, et al. Improved additive-wavelet image fusion[J].
IEEE Geoscience and Remote Sensing Letters, 2011, 8(2): 263–267.
DOI:10.1109/LGRS.2010.2067192 |
| [9] |
KALPOMA K A, KAWANO K, KUDOH J. IKONOS image fusion process using steepest descent method with bi-linear interpolation[J].
International Journal of Remote Sensing, 2013, 34(2): 505–518.
DOI:10.1080/01431161.2012.712233 |
| [10] |
MARCELLO J, MEDINA A, EUGENIO F. Evaluation of spatial and spectral effectiveness of pixel-level fusion techniques[J].
IEEE Geoscience and Remote Sensing Letters, 2013, 10(3): 432–436.
DOI:10.1109/LGRS.2012.2207944 |
| [11] |
ALPARONE L, WALD L, CHANUSSOT J, et al. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest[J].
IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(10): 3012–3021.
DOI:10.1109/TGRS.2007.904923 |
| [12] |
LUO B, KHAN M M, BIENVENU T, et al. Decision-based fusion for pansharpening of remote sensing images[J].
IEEE Geoscience and Remote Sensing Letters, 2013, 10(1): 19–23.
DOI:10.1109/LGRS.2012.2189933 |
 2015, Vol. 44
2015, Vol. 44
