2. 西安通信学院信息服务系 西安 710106;
3. 西安电子科技大学综合业务网国家重点实验室 西安 710071
2. Department of Information Service, Xi'an Communication College Xi'an 710106;
3. State Key Laboratory of Integrated Service Networks, Xidian University Xi'an 710071
为了满足无线网络在吞吐量、传输速率和分集增益等方面的需求,3GPP启动的LTE-Advanced研究项目将协同多点传输(CoMP)和中继技术作为其基本支撑技术[1-2]。基于中继技术的协作通信通过减少发射机和接收机间的传输距离,从而抵抗多径衰落,获得更高的数据传输速率、增加无线信道容量并扩展网络覆盖范围[3],进一步改善无线网络的通信质量。鉴于无线中继技术可为移动通信网络带来上述诸多好处,目前已经成为IMT-Advanced标准的候选技术[4]。
文献[5]提出了网络编码理论,允许网络中间节点进行编码操作,充分利用已有网络资源进行更加有效的数据传输,进一步证明了基于网络编码的多播传输速率可以达到网络流量的理论上限值。鉴于无线网络具有广播特性,网络节点发送的信息可以被其传输范围内的所有节点接收,目前已有很多文献研究无线网络中的网络编码技术。文献[6]基于网络编码技术和物理层广播特性,将无线网络全向传输特性和网络编码技术相结合,提出一种无线网络的分布式传输方案,可以提高无线网络信息交换的吞吐量。在大规模网络中,传统中继方式降低了频谱的有效性,文献[7]提出了自适应网络编码合作传输协议,将瞬时网络图映射为信道编码图。物理层网络编码是一种新的基于电磁波的网络编码方法,利用同时到达电磁波的叠加特性进行伽罗华域网络编码[8],不同于数字比特流上的straightforward网络编码算法,中继节点将接收到的已调电磁波在不解调的情况下,直接进行编码(加和)操作,提高网络吞吐量,减少信息传输时间。文献[9]已将物理层网络编码应用到蜂窝网络上下行传输的联合设计中。为进一步提高网络吞吐量,文献[10-11]提出了复数域网络编码,与伽罗华域网络编码相比,复数域网络编码不仅能获得更好的网络吞吐量性能,还可获得完全分集增益,且不受信噪比以及所采用调制方式的限制。
考虑移动终端处于无线蜂窝小区的边界附近,由于无线信道衰落以及基站发送功率的限制,边界附近的终端用户无法可靠地接收基站信息,为此本文考虑在蜂窝小区内设置中继站点,并给出一种基于复数域网络编码的下行传输方案。对本文方案的符号错误概率(symbol error probability,SEP)性能进行仿真发现,随着中继节点数目的增加其SEP相应地减少,当无线网络具有4个中继节点时,该方案可获得较好的SEP性能。对本文方案进行理论分析表明,比传统中继传输方案能获得更高的网络吞吐量,消耗更少的传输时隙。
1 复数域网络编码方案采用复数域网络编码的信息传输模型[10-11],具有
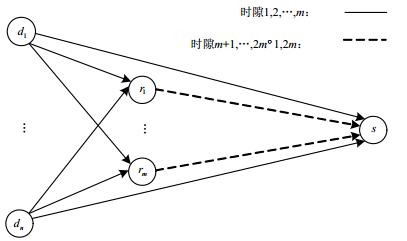 |
| 图1 基于复数域网络编码的协作传输模型 |
| ${y_{d{r_j}}}(t) = \mathit{\boldsymbol{\theta }}_d^{{\rm T}}{\mathit{\boldsymbol{H}}_{d{r_j}}}\mathit{\boldsymbol{x}}(t) + {n_{d{r_j}}}(t) = \sum\limits_{i = 1}^n {{\theta _i}{h_{{d_i}{r_j}}}{x_i}(t)} + {n_{d{r_j}}}(t)$ | (1) |
| ${y_{ds}}(t) = \mathit{\boldsymbol{\theta }}_d^{{\rm T}}{\mathit{\boldsymbol{H}}_{ds}}\mathit{\boldsymbol{x}}(t) + {n_{ds}}(t) = \sum\limits_{i = 1}^n {{\theta _i}{h_{{d_i}s}}{x_i}(t)} + {n_{ds}}(t)$ | (2) |
式中,
在时隙
| $\begin{array}{c} {\hat {\mathit{\boldsymbol{x}}}_j}(t) = \arg \mathop {\min }\limits_{x(t)} {\left\| {{y_{d{r_j}}}(t) - \mathit{\boldsymbol{\theta }}_d^{\rm{T}}{\mathit{\boldsymbol{H}}_{d{r_j}}}\mathit{\boldsymbol{x}}(t)} \right\|^2}{\rm{ = }}\\ \arg \mathop {\min }\limits_{x(t)} {\left\| {{y_{d{r_j}}}(t) - \sum\limits_{i = 1}^n {{\theta _i}{h_{{d_i}{r_j}}}{x_i}(t)} } \right\|^2} \end{array}$ | (3) |
经过
| ${y_{{r_j}s}} = \sqrt {{\alpha _j}} {h_{{r_j}s}}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{\hat x}}_j} + {n_{{r_j}s}}\;\;\;\;j = 1,2, \cdots ,m$ | (4) |
式中,复数域编码系数
| $\begin{array}{c} {{\hat x}_s} = \arg \mathop {\min }\limits_{x'} \left\{ {\sum\limits_{t = 1}^m {{{\left\| {{y_{ds}}(t) - \mathit{\boldsymbol{\theta }}_d^{\rm{T}}{\mathit{\boldsymbol{H}}_{ds}}\mathit{\boldsymbol{x}}(t)} \right\|}^2}} } \right. + \\ \left. {\sum\limits_{j = 1}^m {{{\left\| {{y_{{r_j}s}} - \sqrt {{\alpha _j}} {h_{{r_j}s}}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{x'}}} \right\|}^2}} } \right\} = \\{\rm{ }}\arg \mathop {\min }\limits_{x'} \left\{ {\sum\limits_{t = 1}^m {{{\left\| {{y_{ds}}(t) - \sum\limits_{i = 1}^n {{\theta _i}{h_{{d_i}s}}{x_i}(t)} } \right\|}^2}} } \right. + \\ \left. {{\kern 1pt} \sum\limits_{j = 1}^m {{{\left\| {{y_{{r_j}s}} - \sqrt {{\alpha _j}} {h_{{r_j}s}}{\mathit{\boldsymbol{\theta }}^{\rm{T}}}\mathit{\boldsymbol{x'}}} \right\|}^2}} } \right\} \end{array}$ | (5) |
式中,
图 2所示的蜂窝小区具有3个中继
 |
| 图2 (1, 3, 2)无线中继网络示意图 |
考虑采用中继节点
 |
| 图3 (1, 3, 2)无线中继网络下行信息传输的时隙分配图 |
| ${y_{s{r_1}}} = {h_{s{r_1}}}{x_1} + {n_{s{r_1}}}$ | (6) |
| ${y_{s{r_2}}} = {h_{s{r_2}}}{x_1} + {n_{s{r_2}}}$ | (7) |
| ${y_{s{r_3}}} = {h_{s{r_3}}}{x_1} + {n_{s{r_3}}}$ | (8) |
式中,
| ${\hat x_{1j}} = \arg \mathop {\min }\limits_x {\left\| {{y_{s{r_j}}} - {h_{s{r_j}}}x} \right\|^2}~~~~~j = 1,2,3$ | (9) |
时隙2和时隙3的信息传输过程同时隙1,经过3个时隙,中继节点
| ${c_j} = {\theta} _{1j}{\hat x}_{1j} + {\theta _{2j}}{\hat x_{2j}} + {\theta _{3j}}{\hat x_{3j}} = {\mathit{\boldsymbol{\theta}}} _j^{{\rm T}}{\hat{ {\mathit{\boldsymbol{x}}}}_j}~~~j = 1,2,3$ | (10) |
式中,编码系数向量
在时隙4,中继节点
| $\begin{array}{c} {\rm{ }}{y_{r{d_j}}} = {\rm{ }}\sqrt {{\alpha _1}} {\theta _1}{h_{{r_1}{d_j}}}{c_1} + \sqrt {{\alpha _2}} {\theta _2}{h_{{r_2}{d_j}}}{c_2} + \\ \sqrt {{\alpha _3}} {\theta _3}{h_{{r_3}{d_j}}}{c_3} + {n_{r{d_j}}} = \\ {\rm{ }}\sqrt {{\alpha _1}} {\theta _1}{h_{{r_1}{d_j}}}\mathit{\boldsymbol{\theta }}_1^{\rm{T}}{{\mathit{\boldsymbol{\hat x}}}_1} + \sqrt {{\alpha _2}} {\theta _2}{h_{{r_2}{d_j}}}\mathit{\boldsymbol{\theta }}_2^{\rm{T}}{{\mathit{\boldsymbol{\hat x}}}_2} + \\ \sqrt {{\alpha _3}} {\theta _3}{h_{{r_3}{d_j}}}\mathit{\boldsymbol{\theta }}_3^{\rm{T}}{{\mathit{\boldsymbol{\hat x}}}_3} + {n_{r{d_j}}} = \\ \sum\limits_{i = 1}^3 {\sqrt {{\alpha _i}} {\theta _i}{h_{{r_i}{d_j}}}\mathit{\boldsymbol{\theta }}_i^{\rm{T}}{{\mathit{\boldsymbol{\hat x}}}_i}} + {n_{r{d_j}}} \end{array}$ | (11) |
式中,
| $\begin{array}{c} {{\mathit{\boldsymbol{\hat x}}}_{{d_j}}} = \arg \mathop {\min }\limits_x \left\| {{y_{r{d_j}}} - (\sqrt {{\alpha _1}} {\theta _1}{h_{{r_1}{d_j}}}{c_1} + } \right.\\ {\left. {\sqrt {{\alpha _2}} {\theta _2}{h_{{r_2}{d_j}}}{c_2} + \sqrt {{\alpha _3}} {\theta _3}{h_{{r_3}{d_j}}}{c_3})} \right\|^2} = \\ {\rm{ }}\arg \mathop {\min }\limits_x \left\| {{y_{r{d_j}}} - (\sqrt {{\alpha _1}} {\theta _1}{h_{{r_1}{d_j}}}\mathit{\boldsymbol{\theta }}_1^{\rm{T}}\mathit{\boldsymbol{x}} + } \right.\\ {\left. {\sqrt {{\alpha _2}} {\theta _2}{h_{{r_2}{d_j}}}\mathit{\boldsymbol{\theta }}_2^{\rm{T}}\mathit{\boldsymbol{x}} + \sqrt {{\alpha _3}} {\theta _3}{h_{{r_3}{d_j}}}\mathit{\boldsymbol{\theta }}_3^{\rm{T}}\mathit{\boldsymbol{x}})} \right\|^2} = \\ \arg \mathop {\min }\limits_x {\left\| {{y_{r{d_j}}} - \sum\limits_{i = 1}^3 {\sqrt {{\alpha _i}} {\theta _i}{h_{{r_i}{d_j}}}\mathit{\boldsymbol{\theta }}_i^{\rm{T}}\mathit{\boldsymbol{x}}} } \right\|^2} \end{array}$ | (12) |
对上述(1, 3, 2)无线中继网络中基于复数域网络编码的下行信息传输过程进行分析,基站
将基于复数域网络编码下行传输方案从(1, 3, 2)无线中继网络推广到具有
 |
| 图4 (1, m, n)无线中继网络下行信息传输的时隙分配图 |
| ${y_{s{r_j}}} = {h_{s{r_j}}}{x_i} + {n_{s{r_j}}}$ | (13) |
式中,
| ${\hat x_{ij}} = \arg \mathop {\min }\limits_x {\left\| {{y_{s{r_j}}} - {h_{s{r_j}}}x} \right\|^2}$ | (14) |
| ${c_j} = {\theta _{1j}}{\hat x_{1j}} + {\theta _{2j}}{\hat x_{2j}} + \cdots + {\theta _{mj}}{\hat x_{mj}} = \mathit{\boldsymbol{\theta }}_j^{\rm{T}}{\mathit{\boldsymbol{\hat x}}_j}$ | (15) |
在时隙
| $\begin{array}{c} {y_{r{d_j}}} = {\rm{ }}\sqrt {{\alpha _1}} {\theta _1}{h_{{r_1}{d_j}}}{c_1} + \sqrt {{\alpha _2}} {\theta _2}{h_{{r_2}{d_j}}}{c_2} + \cdots + \\ \sqrt {{\alpha _m}} {\theta _m}{h_{{r_m}{d_j}}}{c_m} + {n_{r{d_j}}} = \\ \sqrt {{\alpha _1}} {\theta _1}{h_{{r_1}{d_j}}}\mathit{\boldsymbol{\theta }}_1^{\rm{T}}{{\mathit{\boldsymbol{\hat x}}}_1} + \sqrt {{\alpha _2}} {\theta _2}{h_{{r_2}{d_j}}}\mathit{\boldsymbol{\theta }}_2^{\rm{T}}{{\mathit{\boldsymbol{\hat x}}}_2} + \cdots + \\ \sqrt {{\alpha _m}} {\theta _m}{h_{{r_m}{d_j}}}\mathit{\boldsymbol{\theta }}_m^{\rm{T}}{{\mathit{\boldsymbol{\hat x}}}_m} + {n_{r{d_j}}} = \\ \sum\limits_{i = 1}^m {\sqrt {{\alpha _i}} {\theta _i}{h_{{r_i}{d_j}}}\mathit{\boldsymbol{\theta }}_i^{\rm{T}}{{\mathit{\boldsymbol{\hat x}}}_i}} + {n_{r{d_j}}} \end{array} $ | (16) |
式中,
| $\begin{array}{c} {{\mathit{\boldsymbol{\hat x}}}_{{d_j}}} = \arg \mathop {\min }\limits_x \left\| {{y_{r{d_j}}} - ({\rm{ }}\sqrt {{\alpha _1}} {\theta _1}{h_{{r_1}{d_j}}}{c_1} + \sqrt {{\alpha _2}} {\theta _2}{h_{{r_2}{d_j}}}{c_2} + } \right. \cdots + \\ {\left. {\sqrt {{\alpha _m}} {\theta _m}{h_{{r_m}{d_j}}}{c_m})} \right\|^2} = \arg \mathop {\min }\limits_x \left\| {{y_{r{d_j}}} - (\sqrt {{\alpha _1}} {\theta _1}{h_{{r_1}{d_j}}}\mathit{\boldsymbol{\theta }}_1^{\rm{T}}\mathit{\boldsymbol{x}} + } \right.\\ {\left. {\sqrt {{\alpha _2}} {\theta _2}{h_{{r_2}{d_j}}}\mathit{\boldsymbol{\theta }}_2^{\rm{T}}\mathit{\boldsymbol{x}} + \cdots + \sqrt {{\alpha _m}} {\theta _m}{h_{{r_m}{d_j}}}\mathit{\boldsymbol{\theta }}_m^{\rm{T}}\mathit{\boldsymbol{x}})} \right\|^2} = \\ \arg \mathop {\min }\limits_x {\left\| {{y_{r{d_j}}} - \sum\limits_{i = 1}^m {\sqrt {{\alpha _i}} {\theta _i}{h_{{r_i}{d_j}}}\mathit{\boldsymbol{\theta }}_i^{\rm{T}}\mathit{\boldsymbol{x}}} } \right\|^2} \end{array}$ | (17) |
(1, m, n)无线中继网络采用基于复数域网络编码的下行传输方案,基站
无线中继网络中用户节点在基站
 |
| 图5 传统中继转发下行传输方案的时隙分配图 |
| $\begin{gathered} {y_{r{d_j}}} = \sqrt {{\alpha _1}} {h_{{r_1}{d_j}}}{{\hat x}_1} + \sqrt {{\alpha _2}} {h_{{r_2}{d_j}}}{{\hat x}_2} + \cdots + \\ \sqrt {{\alpha _m}} {h_{{r_m}{d_j}}}{{\hat x}_m} + {n_{r{d_j}}} = \sum\limits_{i = 1}^m {\sqrt {{\alpha _i}} {h_{{r_i}{d_j}}}} {{\hat x}_i} + {n_{r{d_j}}} \\ \end{gathered} $ | (18) |
采用最大似然检测,用户节点
| $\begin{gathered} {{\hat x}_{{d_j}}} = \arg \mathop {\min }\limits_{x \in A} \left\| {{y_{r{d_j}}} - \left( {\sqrt {{\alpha _1}} {h_{{r_1}{d_j}}}x + \sqrt {{\alpha _2}} {h_{{r_2}{d_j}}}x + \cdots + } \right.} \right. \\ {\left. {\left. {\sqrt {{\alpha _m}} {h_{{r_m}{d_j}}}x} \right)} \right\|^2} = \arg \mathop {\min }\limits_{x \in A} {\left\| {{y_{r{d_j}}} - \sum\limits_{i = 1}^m {\sqrt {{\alpha _i}} {h_{{r_i}{d_j}}}} x} \right\|^2} \\ \end{gathered} $ | (19) |
基于传统中继转发的下行信息传输方案中,基站
通过对上述方案的网络吞吐量性能进行分析,当无线中继网络存在单一中继节点时,基于复数域网络编码的下行信息传输方案获得与传统中继转发方案相同的网络吞吐量1/2符号/时隙;当中继节点数
采用C++语言进行仿真实验,对不同SNR下基于复数域网络编码下行传输方案的SEP进行比较。仿真过程中采用性能最好的BPSK调制。
基于复数域网络编码下行传输方案的SEP仿真结果如图 6所示。从SEP曲线可以看出,无线中继网络具有
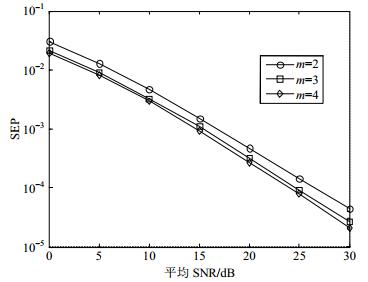 |
| 图6 基于复数域网络编码下行传输方案的SEP |
 |
|
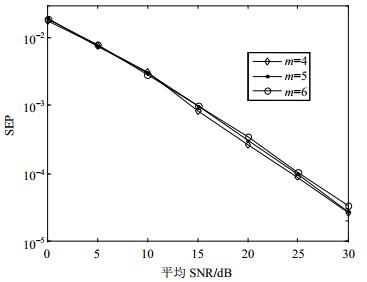
图7
具有 |
当中继节点数
在仿真过程中,中继节点上得到的复数域编码符号
无线中继网络采用传统中继传输方案的SEP仿真结果如图 8所示。当中继节点数
 |
| 图8 传统中继传输方案的SEP |
由于无线信道衰落以及基站发送功率的限制,蜂窝小区边界处的移动终端无法可靠地接收基站信息,考虑在蜂窝小区内设置中继站点,提出一种基于复数域网络编码的下行传输方案。该方案的SEP明显低于传统中继转发方案,且该方案将获得更高的信息传输速率和网络吞吐量。需要指出,由于提出的下行传输方案里中继节点需进行复数域网络编码,而且用户节点需对复数域编码符号进行最大似然检测,相对于传统中继转发方案,中继节点和用户节点执行的复杂度略高,消耗的时间也比传统方案略多。
本文研究得到了西安市科技计划项目(CXY1340(4))的支持,在此表示感谢。
| [1] |
SAWAHASHI M, KISHIYAMA Y, MORIMOTO A, et al. Coordinated multipoint transmission/reception techniques for LTE-advanced[J].
IEEE Wireless Communications, 2010, 17(3): 26–34.
DOI:10.1109/MWC.2010.5490976 |
| [2] |
TEYEB O, FREDERIKSEN F, PHAN V V, et al. User multiplexing in relay enhanced LTE-advanced networks[C]// 2010 IEEE 71st Vehicular Technology Conference (VTC 2010-Spring). Taipei, China: IEEE Press, 2010: 1-5.
http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=5493983 |
| [3] |
LANEMAN J N, WORNELL G W. Distributed space- time-coded protocols for exploiting cooperative diversity in wireless networks[J].
IEEE Trans on Information Theory, 2003, 49(10): 2415–2425.
DOI:10.1109/TIT.2003.817829 |
| [4] |
YANG Y, HU H, XU J, et al. Relay technologies for WiMAX and LTE-Advanced mobile systems[J].
IEEE Communications Magazine, 2009, 47(10): 100–105.
DOI:10.1109/MCOM.2009.5273815 |
| [5] |
AHLSWEDE R, CAI N, LI S Y R, et al. Network information flow[J].
IEEE Trans on Information Theory, 2000, 46(4): 1204–1216.
DOI:10.1109/18.850663 |
| [6] |
WU Y, CHOU P A, KUNG S Y. Information exchange in wireless networks with network coding and physical-layer broadcast[C]//Proceedings of the 2005 Conference on Information Sciences and Systems. Baltimore: IEEE Press, 2005.
https://www.researchgate.net/publication/228701799_Information_exchange_in_wireless_networks_with_network_coding_and_physical-layer_broadcast |
| [7] |
BAO X, LI J. Adaptive network coded cooperation (ANCC) for wireless relay networks: matching code-on-graph with network-on-graph[J].
IEEE Transactions on Wireless Communications, 2008, 7(2): 574–583.
DOI:10.1109/TWC.2008.060439 |
| [8] |
ZHANG S, LIEW S C, LAM P. On the synchronization of physical-layer network coding[C]//Proceedings of the 2006 IEEE Information Theory Workshop. Chengdu: IEEE Press, 2006: 404-408.
http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=4119328 |
| [9] |
ZHIGUO D, KRIKIDIS I, THOMPSON J, et al. Physical layer network coding and precoding for the two-way relay channel in cellular systems[J].
IEEE Transactions on Signal Processing, 2011, 59(2): 696–712.
DOI:10.1109/TSP.2010.2081985 |
| [10] |
WANG T, GIANNAKIS G B. Complex field network coding for multiuser cooperative communications[J].
IEEE Journal on Selected Areas in Communications, 2008, 26(3): 561–571.
DOI:10.1109/JSAC.2008.4481380 |
| [11] |
WANG T, GIANNAKIS G B. High-throughput cooperative communications with complex field network coding[C]// The 41st Annual Conference on Information Sciences and Systems. Baltimore, USA: IEEE Press, 2007: 253-258.
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4298309 |
| [12] |
XIN Y, WANG Z, GIANNAKIS G B. Space-time diversity systems based on unitary constellation-rotating precoders [C]//IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP '01). Salt Lake City, UT: IEEE Press, 2001: 2429-2432.
http://doi.ieeecomputersociety.org/10.1109/ICASSP.2001.940491 |
| [13] |
VISHWANATH R, BHATNAGAR M R. Optimum linear constellation precoding for space time wireless systems[J].
Wireless Personal Communications, 2007, 40(4): 511–521.
DOI:10.1007/s11277-006-9118-6 |
| [14] |
BERNARD S.
Digital communications: fundamentals and applications[M]. 2nd ed. New Jersey: Prentice Hall PTR, 2001.
|
 2015, Vol. 44
2015, Vol. 44
