2. 电子科技大学电子工程学院 成都 611731
2. School of Electronic Engineering, University of Electronic Science and Technology of China Chengdu 611731
遥感卫星上不同类型的传感器能生成地面不同类型的观测图像,通常有全色图像(pan-chormatic image)和多光谱图像(multispectral image)两类。全色图像每个像素包含传感器能观测到的整个光谱中的辐射信息,拥有高空间分辨率;多光谱图像则能提供不同光谱子带内的辐射信息,拥有高光谱分辨率。在应用中,往往期望能使用同时具有高空间分辨率和高光谱分辨率的图像,有必要研究全色图像与多光谱图像的遥感图像融合方法(简称遥感图像融合方法)。
遥感图像融合方法的研究已经持续了几十年。在早期的研究中,融合图像是按一定的权值做加权平均,如Brovery变换[1],这类方法简单,易实现,但融合图像质量低,很多边缘等信息出现模糊。人们逐渐认识到光谱信息的重要性,提出了以IHS变换(intensity, hue, saturation)[2]、PCA(principle component analysis)[3]等方法为代表、能有效地保持光谱信息的融合方法。这些方法中,多光谱图像的亮度分量或主分量完全被全色图像替代,导致融合图像中光谱信息被过度抑制。而基于多尺度变换的方法无需将整个分量进行替换,更灵活地保留空间和光谱信息。常用的变换包括离散小波变换[3]、解析小波变换[4]、双树复数小波变换(dual tree complex wavelet transform,DT CWT)[5-6]、Curvelet变换[7-8]等;且这些方法往往和IHS或PCA结合起来。
剪切波变换是近年来被提出且逐渐成熟起来,能高效表示多维数据的超小波变换。传统的多尺度方法缺乏对具有方向性特征高效表示的能力。而在各种具有对方向表达能力的超小波变换中,剪切波是唯一同时拥有以下优点的变换:只有一个或有限个产生函数集,能几乎最优地表示高维数据,连续和离散数据处理方式相同,空域紧支实现等。当前,剪切波有频域实现和空域实现两类离散实现。频域实现具有更高的频域局部特性,而空域实现则具有更高的空域局部特性。自然图像中边缘等重要信息往往具有空域局部性,且视觉系统直接通过空域获取信息,因此本文选用空域实现——紧支剪切波变换[9-10](compactly supported shearlet transform,CSST)作为融合方法的变换。传统的CSST采用了移变的离散小波变换(discrete wavelet transform,DWT),会降低融合图像质量。目前已提出了一些基于剪切波的图像融合方法。文献[11]提出了基于频域实现剪切波的遥感图像融合方法,性能优于Curvelet变换。文献[12-13]讨论了基于CSST的多焦距图像融合方法,但没有考虑移变性的影响,也没采取措施消除移变性。文献[14]提出结合IHS和剪切波变换的遥感图像融合方法,但没说明到底采用哪种剪切波变换。
本文首先分析移变性对融合算法性能的影响,进而提出采用双树结构来消除CSST的移变性,称为双树紧支剪切波变换(dual tree compactly supported shearlet transform,DT CSST)。最后提出基于DT CSST和IHS或PCA结合的遥感图像融合方法。
1 双树紧支剪切波变换剪切波是复合伸缩小波的一种[15],前期研究表明其空域实现相对频域实现失真更少,但传统空域实现是移变的。首先通过仿真来说明移变性对图像融合方法性能的影响,再通过双树结构改进CSST,本文称改进后的变换为双树紧支剪切波变换(DT CSST)。
图 1a、1b是两幅仿真源图像,分别用plot和mesh方式显示。图 1a是明亮而细的环位于黑色背景中央;图 1b是暗淡而粗的环位于黑色背景中央。仿真源图像通过通用融合框架(将在2.1节介绍)融合的图像,融合准则是取系数幅值较大者。图 1c、图 1d是融合图像:图 1c是基于移变的DWT的融合结果,图 1d是基于(几乎)移不变的DT CWT的融合结果。无论是从plot还是从mesh图都能看出,左边融合图像圆环的顶部出现波浪起伏,而右边环顶端是平的。这些起伏是由变换移变性引起的。因为移变性使得同样的信号在不同位置以不同的方式“投影”到各层系数中,即不同位置的相同信号其分解系数不同,且差别明显。这样的差别很难通过融合准则予以区分(实验发现,即使更换其他的融合准则,也不能完全消除移变性带来的影响),最终导致融合图像出现波浪状的起伏(失真),在背景部分同样存在失真,本质上是圆环部分信号的能量泄露到背景中。
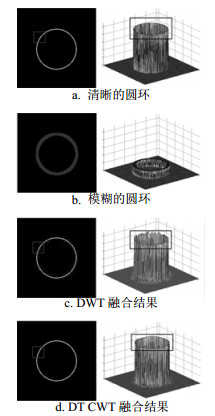 |
| 图1 DWT和DT CWT重建图像 |
文献[9]提出了紧支剪切波CSST的构造方法,分为两个步骤:1)分别在水平和垂直锥上做shear操作;2)各向异小波变换(anisotropic DWT,ADWT)。双树复数小波变换[16-17],通过两组独立且构成希尔伯特变换对的尺度和小波滤波器对信号进行分解,分别模拟复数小波变换的实部和虚部。两组滤波器能分别独立重建信号,但变换系数的模值是(几乎)移不变的。为消除CSST的移变性,本文采用DT CWT替代ADWT。
本文采用文献[16-17]中DWT移变性和DT CWT移不变性的方法来展示CSST和DT CSST的区别。图 2a表示所有系数重建图像,白色的圆位于黑色背景中央,与仿真源图像一致。图 2b表示单独由低频系数重建的图像;图 2c~图 2g分别表示仅由5层高频系数单独重建的图像,每个分图从上至下依次是DT CSST垂直锥、CSST垂直锥、DT CSST水平锥和CSST水平锥在某方向上的重建图像。CSST和DT CSST都能重构输入图像,消除移变性的DT CSST低频和每层高频系数的重构图像非常平滑,而CSST的低频和每层高频图像重构图像不平滑。这反映出DT CSST是移不变的而CSST是移变的,即本文的方法能有效地抑制CSST的移变性。
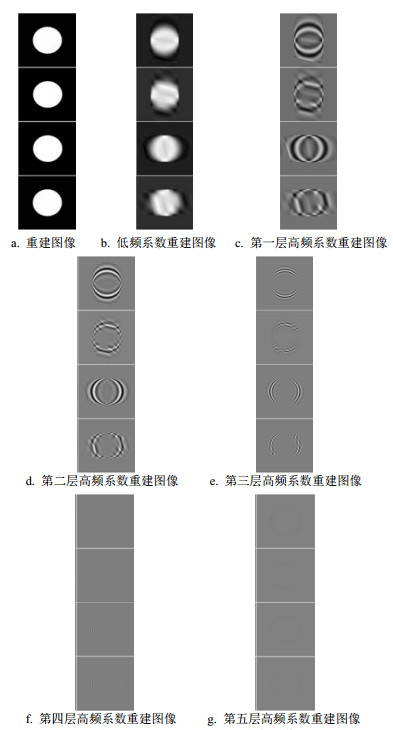 |
| 图2 CSST和DT CSST重建图像 |
本文首先介绍基于DT CSST的通用融合框架(general image fusion,GIF),如图 3所示。A、B分别表示输入的源图像,通过DT CSST正变换,输出系数CA、CB,在按一定的融合准则进行融合后得到融合系数,用CF表示,通过DT CSST逆变换后输出为融合图像,用F表示。融合准则公式为:
| $ \left\{ \begin{align} &{{C}_{\text{FL}}}={\text{mean}}({{C}_{\text{AL}}}+{{C}_{\text{BL}}}) \\ &{{C}_{\text{FH}}}={{C}_{\text{AH}}} \\ \end{align} \right. $ | (1) |
 |
| 图3 通用融合框架 |
式中,mean表示求取均值;下标L表示低频;下标H表示高频。
IHS变换中I表示亮度,H表示色度,S表示饱和度,是颜色空间的一种表示,与常用的RGB(红绿蓝)可表示为:
| $ \begin{align} & \left( \begin{matrix} I \\ {{v}_{1}} \\ {{v}_{2}} \\ \end{matrix} \right)=\left( \begin{matrix} \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & \frac{-2}{\sqrt{6}} \\ \frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{2}} & 0 \\ \end{matrix} \right)\left( \begin{matrix} R \\ G \\ B \\ \end{matrix} \right) \\ & \left( \begin{matrix} R \\ G \\ B \\ \end{matrix} \right)=\left( \begin{matrix} \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} & \frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{3}} & \frac{1}{\sqrt{6}} & \frac{-1}{\sqrt{2}} \\ \frac{1}{\sqrt{3}} & \frac{-2}{\sqrt{6}} & 0 \\ \end{matrix} \right)\left( \begin{matrix} I \\ {{v}_{1}} \\ {{v}_{2}} \\ \end{matrix} \right) \\ & H={{\tan }^{-1}}\left( \frac{{{v}_{\rm{2}}}}{{{v}_{\rm{1}}}} \right), \ \ S=\sqrt{v_{1}^{2}+v_{2}^{2}} \\ \end{align} $ | (2) |
式中,v1、v2是中间变量。
PCA(primary component analysis)变换是一种分析、简化数据集的技术。主成分分析经常用于减少数据集的维数,同时保持数据集中的对方差贡献最大的特征。这是通过保留低阶主成分,忽略高阶主成分做到的。这样低阶成分能够保留住数据的最重要信息。通常情况下,该运算可以看作能揭露数据的内部结构,更好地分析解译数据的变量的方法。如果一个多元数据集能够在一个高维坐标系中被完整表示,那么通过PCA变换,就能得到一幅低维度的图像,这幅图像即为高维空间数据在低维空间上的“投影”,虽然信息上有一定的损失,但能降低数据的维数,节省存储和通信资源。
PCA与IHS在遥感融合算法中最大区别是IHS只能处理3分量多光谱图像,而PCA能处理任意多分量的光谱图像。本文提出的融合具体步骤如图 4所示,多光谱图像RGB分量缩放到与全色图一样尺寸,再进行正IHS或PCA变换,得到的亮度分量或第一分量在图中表示为C1,全色图像参考C1的直方图进行直方图均衡(histogram equilibrium,HE),再通过通用融合框架进行图像融合,得到的结果与其余分量做逆IHS或逆PCA变换,形成最终融合图像。
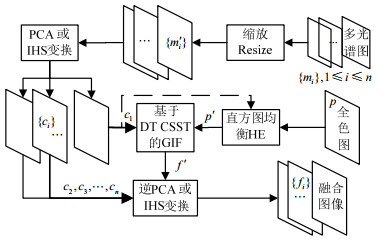 |
| 图4 本文方法步骤 |
融合图像的质量通过两类评价指标来表示,一类是空间一致性指标,包括互信息量MI,如QAB|F[18]、Q0[19];另一类是光谱一致性指标,包括RASE、ERGAS和Q3[2]。
QAB|F衡量了融合图像从源图像中提取的边缘信息,取值(0, 1),QAB|F越接近1,说明从源中得到的信息越多。
| $ {{Q}_{0}}=\frac{4{{\sigma }_{xy}}\bar{x}\bar{y}}{({{{\bar{x}}}^{2}}+{{{\bar{y}}}^{2}})(\sigma _{x}^{2}+\sigma _{y}^{2})}=\frac{{{\sigma }_{xy}}}{{{\sigma }_{x}}{{\sigma }_{y}}}\frac{2\bar{x}\bar{y}}{{{{\bar{x}}}^{2}}+{{{\bar{y}}}^{2}}}\frac{2{{\sigma }_{x}}{{\sigma }_{y}}}{\sigma _{x}^{2}+\sigma _{y}^{2}} $ | (3) |
式中,x和y代表输入图像;x和y是x和y的均值;
RASE为:
| $ \rm{RASE}=\frac{100}{\mathit{M}}\sqrt{\frac{1}{\mathit{N}}\sum\limits_{\mathit{i}=1}^{\mathit{N}}{\rm{RMS}{{\rm{E}}^{2}}({{\mathit{S}}_{\mathit{i}}})}} $ | (4) |
式中,M是N个分量图像(Si)辐射强度的均值;RMSE代表均方根误差,
ERGAS表示所有维上的合成误差,有:
| $ {\text{ERGAS}}=100\frac{h}{l}\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}{\frac{{\text{RMS}}{{\text{E}}^{2}}({{S}_{i}})}{M_{i}^{2}}}} $ | (5) |
式中,h是全色图的分辨率;l是多光谱图的分辨率;Mi是每个分量的辐射均值。RASE和ERGAS越小,代表光谱一致性越高。
源多光谱图像的3个分量分别用a1、b1和c1表示,融合结果的3个分量用a2、b2和c2表示,而源多光谱图像和融合图像可用
| $ {{Q}_{3}}=\frac{\left| {{\sigma }_{{{z}_{1}}{{z}_{2}}}} \right|}{{{\sigma }_{{{z}_{1}}}}{{\sigma }_{{{z}_{2}}}}}\frac{2{{\sigma }_{{{z}_{1}}}}{{\sigma }_{{{z}_{2}}}}}{\sigma _{{{z}_{1}}}^{2}+\sigma _{{{z}_{2}}}^{2}}\frac{2\left| {{{\bar{z}}}_{1}} \right|\left| {{{\bar{z}}}_{2}} \right|}{{{\left| {{{\bar{z}}}_{1}} \right|}^{2}}+{{\left| {{{\bar{z}}}_{2}} \right|}^{2}}} $ | (6) |
Q3本质上是Q0的向量版,其各个参数定义与Q0一致,当Z1与Z2相等时,取最大值1。
3 实验和分析实验采用3组卫星数据作为源数据,对本文方法和其对比方法进行验证:第一、二组是IKONOS卫星数据,分别如图 5、图 6所示;第三组是QuickBird卫星数据,如图 7所示。IKONOS全色图的空间分辨率为1 m,多光谱图像的空间分辨率为4 m,QuickBird则分别为0.6 m和2.4 m。全色图像尺寸为512×512,多光谱图像尺寸为128×128,源图像由图 5a、图 5b及图 7a、图 7b表示,多光谱图像已缩放至与全色图一样尺寸。图 5c、图 5d及图 7c、图 7d为本文提出的DT CSST+IHS和DT CSST+PCA的最终融合图像。其余为对比方法的最终融合图像。图 5e、图 6e、图 7e为Curvelet + IHS,图 5f、图 6f、图 7f为DT CWT + IHS,图 5g、图 6g、图 7g为à trous wavelet + IHS,图 5h、图 6h、图 7h为à trous shearlet + IHS,图 5i、图 6i、图 7i为Curvelet + PCA,图 5j、图 6j、图 7j为DT CWT + PCA,图 5k、图 6k、图 7k为à trous wavelet + PCA,图 5l、图 6l、图 7l为à trous shearlet + PCA。观察各个融合图像,除DWT外,结果非常相近。说明本文的方法与对比方法一样,都能有效地完成遥感图像融合的任务,但单纯通过观察融合图像的视觉效果很难分辨方法性能的优劣。
 |
| 图5 第一组数据的源图像和融合结果 |
 |
| 图6 第二组数据的源图像和融合结果 |
 |
| 图7 第三组数据的源图像和融合结果 |
由于篇幅的限制,本文只给出第一组数据基于IHS变换部分(尺度参数2至4)的性能指标。通过表 1、表 2,可看出空间一致性和光谱一致性实际上是一组互斥的指标,提高空间一致性往往会导致光谱一致性的下降,反之亦然;而在所有的方法中没有一种方法能在空间一致性高于其余方法的同时,使得光谱一致性也高于其他方法,即单纯观察性能指标的数值仍然无法有效地衡量不同算法性能的好坏。但是将空间一致性指标和光谱一致性指标作为两个坐标轴,将每个点连起来,就能看出端倪来。由于篇幅限制,图 8只给出了3组数据横坐标为MI、纵坐标为Q3和RASE的情况,三行图像依次为第一、第二和第三组数据的情况。通过图 8可以看出,基于DWT的方法与其他方法性能差别较大,曲线离的比较远,而本文的方法(黑色线条)在scale参数取2~6时位于图的最右端,即在同样的空间一致性性能时,本文的方法具有最高的光谱一致性,而在具有同样的光谱一致性时,本文的方法具有最好的空间一致性。尺度参数过高会导致运算量的增加,且融合图像含有过多的光谱信息,不可取。因此,本文的方法性能优于其他方法。
| 表1 IHS变换所有方法空间一致性指标 |
| 表2 IHS变换所有方法频谱一致性指标 |
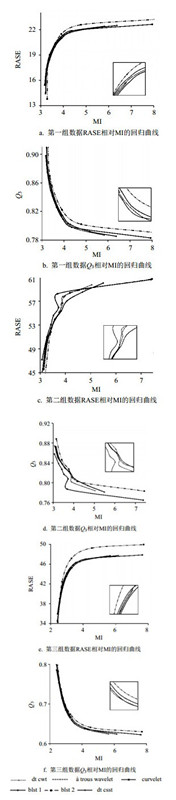 |
| 图8 3组数据IHS变换性能指标图 |
本文提出了基于双树紧支剪切波和IHS或PCA变换的遥感图像融合算法。双树紧支剪切波变换能有效地消除传统的紧支剪切波变换的移变性的缺点。将双树紧支剪切波与IHS或PCA相结合的遥感图像融合方法,能高效地完成遥感图像融合算法。通过IKONOS和QuickBird卫星图像数据进行融合,本文的方法优于基于DWT、DT CWT、Curvelet、à trous wavelet以及频域剪切波实现à trous剪切波的方法。
| [1] |
ELGHAZALI E S. Performance of quickbird image and lidar data fusion for 2d/3d city mapping[J].
Australian Journal of Basic and Applied S ciences, 2011, 5(11): 1588–1600.
|
| [2] |
CHOI M. A new intensity-hue-saturation fusion approach to image fusion with a tradeoff parameter[J].
IEEE Transactions on Geoscience and Remote Sensing, 2006, 44(6): 1672–1682.
DOI:10.1109/TGRS.2006.869923 |
| [3] |
GONZÁLEZ-AUDÍCANA M, SALETA J L, CATALAN R G, et al. Fusion of multispectral and panchromatic images using improved IHS and PCA mergers based on wavelet decomposition[J].
IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(6): 1291–1299.
DOI:10.1109/TGRS.2004.825593 |
| [4] |
NUNEZ J, Otazu X, Fors O, et al. Multiresolution-based image fusion with additive wavelet decomposition[J].
IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(3): 1201–1211.
|
| [5] |
IOANNIDOU S, KARATHANASSI V. Investigation of the dual-tree complex and shift-invariant discrete wavelet transforms on quickbird image fusion[J].
Geoscience and Remote Sensing Letters, 2007, 4(1): 166–170.
DOI:10.1109/LGRS.2006.887056 |
| [6] |
WANG P F, DU Y F, ZHOU H F, et al. A parallel fusion algorithm for remote sensing image based on complex wavelet transform[J].
Computer Engineering and Science, 2008, 30(3): 35–39.
|
| [7] |
Guo L, Dai M, Zhu M. Multifocus color image fusion based on quaternion curvelet transform[J].
Optics Express, 2012, 20(17): 18846–18860.
DOI:10.1364/OE.20.018846 |
| [8] |
ZHANG Q, GUO B L. Fusion of remote sensing images based on the second generation curvelet transform[J].
Optics and Precision Engineering, 2007, 7(15): 1131–1135.
|
| [9] |
LIM W Q. The discrete shearlet transform: a new directional transform and compactly supported shearlet frames[J].
IEEE Trans Image Process, 2010, 19(5): 1166–80.
DOI:10.1109/TIP.2010.2041410 |
| [10] |
Kutyniok G, LIM W Q. Compactly supported shearlets are optimally sparse[J].
Journal of Approximation Theory, 2011, 163(11): 1564–1589.
DOI:10.1016/j.jat.2011.06.005 |
| [11] |
Chai Y, He Y, Qu C. Remote sensing image fusion based on iterative discrete Shearlet transform[J].
Computer Engineering and Applications, 2011, 47(3): 174–176.
|
| [12] |
Miao Q, Shi C, Xu P, et al. A novel algorithm of image fusion using shearlets[J].
Optics Communications, 2011, 284(6): 1540–1547.
DOI:10.1016/j.optcom.2010.11.048 |
| [13] |
Miao Q, Shi C, Xu P, et al. Multi-focus image fusion algorithm based on shearlets[J].
Chinese Optics Letters, 2011, 9(4): 041001.
DOI:10.3788/COL |
| [14] |
DENG C, WANG S, CHEN X. Remote sensing images fusion algorithm based on shearlet transform[C]// Environmental Science and Information Application Technology. [S. l]: [s. n. ], 2009.
|
| [15] |
Easley G R, labate d. Critically sampled wavelets with composite dilations[J].
IEEE Image Processing, Transactions on, 2012, 21(2): 550–561.
DOI:10.1109/TIP.2011.2164415 |
| [16] |
KINGSBURY N. Complex wavelets for shift invariant analysis and filtering of signals[J].
Applied and Computational Harmonic Analysis, 2001(10): 234–253.
|
| [17] |
KINGSBURY N. Image processing with complex wavelets[J].
Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 1999(357): 2543–2560.
|
| [18] |
PETROVI V, XYDEAS C. On the effects of sensor noise in pixel-level image fusion performance[C]//Information Fusion, Proceedings of the Third International Conference. [S. l]: [s. n. ], 2000.
|
| [19] |
PIELLA G, HEIJMANS H. A new quality metric for image fusion[C]//Image Processing, 2003 International Conference. [S. l]: [s. n. ], 2003.
|
| [20] |
WANG Z, BOVIK A C. A universal image quality index[J].
Signal Processing Letters, IEEE, 2002(9): 81–84.
|
 2015, Vol. 44
2015, Vol. 44
