2. 电子科技大学能源科学与工程学院 成都 611731
2. School of Energy Science and Engineering, University of Electronic Science and Technology of China Chengdu 611731
机器人系统含有不同类型的不确定性因素[1],如参数不确定性(如机器人连杆质量、连杆长度等物理量未知)和外部干扰(如所处的作业环境干扰、摩擦、负载扰动等)。上述不确定性的存在可能会影响系统的控制精度,甚至引起系统不稳定,因此需要设计恰当的控制方案以保证系统的稳定性和位置跟踪性能。
在各种控制策略中,自适应控制是处理不确定性机器人系统的一种有效方法,它对结构已知而参数未知的对象具有很好的控制效果,因此在不确定性机器人系统的控制中得到了广泛的应用。这方面创始性的且最有影响力的是文献[2-4]的工作。近年来,又出现了一些关于机器人的新型自适应控制算法[5-6]。对于机器人位置轨迹的跟踪,文献[5]针对机器人模型中的动力学和运动学参数不确定性,提出了一种基于近似雅可比的自适应控制方法。文献[6]提出了一个自适应控制器以补偿机器人模型中的线性化和非线性参数不确定性。但是需要指出的是,自适应控制的本质基于动力学模型,它对非参数的不确定性,如外部干扰的抑制效果不是很理想。
干扰观测器可以弥补自适应控制的不足,对不可预测的或随机的外部干扰具有很好的抑制效果。非线性干扰观测器的控制方案也已经在机器人控制领域得到了广泛地应用[7-8]。文献[7]针对具有不确定干扰的两连杆机器人系统设计了一种非线性干扰观测器,通过选择合适的设计参数使干扰观测器的指数渐近稳定性可以得到保证,该干扰观测器可用于机器人系统中的摩擦补偿、独立关节控制、无传感器转矩控制以及故障诊断。文献[8]对文献[7]的工作进行了扩展,提出了一种可用于n连杆机器人系统的非线性干扰观测器。但上述这些已有的干扰观测器方法中都没有考虑机器人系统中可能含有的未知死区特性。
结合自适应控制器和干扰观测器的各自优点,本文设计了一种基于干扰观测器的自适应控制器,处理具有外部干扰、内部动力学参数不确定性以及未知死区特性的一类不确定机器人系统。其中,非线性干扰观测器对外部干扰进行估计和补偿,自适应控制器则处理内部不确定的动力学参数和未知的死区特性。
1 机器人系统非线性数学模型当考虑外部干扰时,n-自由度机器人的关节空间非线性动力学为[9]:
| $\mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) = \mathit{\boldsymbol{\tau }} + \mathit{\boldsymbol{d}}$ | (1) |
式中,
性质1[10] 惯量矩阵
性质2[10] 式(1)左边的项关于动力学参数向量
| $ \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) = \mathit{\boldsymbol{Y}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}},\mathit{\boldsymbol{\ddot q}})\mathit{\boldsymbol{\theta }} $ |
式中,
机器人系统式(1)除了受到外部干扰的影响,还可能受到内部动力学参数不确定性的影响。当系统中存在动力学参数不确定性时,利用性质2,式(1)的左边变为:
| $ \mathit{\boldsymbol{\hat M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{\hat C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{\hat G}}(\mathit{\boldsymbol{q}}) = \mathit{\boldsymbol{Y\hat \theta }} $ | (2) |
式中,
| $ {\tau _{_i}}(t) = {\rm{D}}{{\rm{Z}}_i}({v_i}(t)) =\\ \left\{ \begin{array}{l} {m_{{{\text{r}}_i}}}({v_i}(t) - {b_{{{\text{r}}_i}}})\;\;\;\;\;\;\;{\rm{if}}\quad {v_i}(t) \ge {b_{{{\text{r}}_i}}}\\ {\rm{0}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{if }}\quad {b_l} < {v_i}(t) < {b_{{{\text{r}}_i}}}\\ {m_{{{\text{l}}_i}}}({v_i}(t) - {b_{\text{l}}}_{_i})\;\;\;\;\;\;\;\;{\rm{if}}\quad {v_i}(t) \le {b_{{{\text{l}}_i}}} \end{array} \right. $ | (3) |
式中,
本文所设计的基于干扰观测器的自适应控制方案的结构如图 1所示。
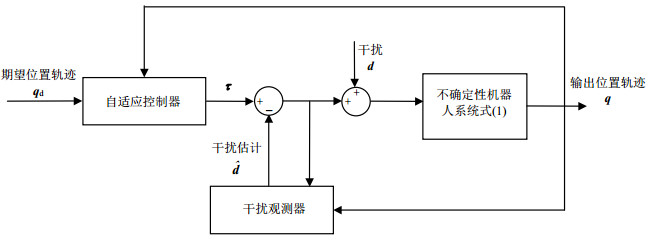 |
| 图1 不确定机器人系统基于干扰观测器的自适应控制框图 |
图 1中,非线性干扰观测器对外部干扰
本文在文献[7]工作基础上,对受到外部干扰的机器人系统式(1)设计非线性干扰观测器为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\dot {\hat d}}} = - \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\hat d}} + \\ \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})[\mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) - \mathit{\boldsymbol{\tau }}] \end{array} $ | (4) |
式中,
将动力学方程式(1)代入上面的非线性干扰观测器式(4)中,则得到干扰观测误差的动力学为:
| $ \mathit{\boldsymbol{\dot {\hat d}}} = - \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\hat d}} + \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{d}} = \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\Delta \mathit{\boldsymbol{d}} $ | (5) |
式中,
| $ \Delta \mathit{\boldsymbol{\dot d}} + \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\Delta \mathit{\boldsymbol{d}} = 0 $ | (6) |
由干扰观测误差的动力学方程式(6)知,如果
采用干扰观测器对外部干扰进行估计后,可以设计自适应控制器对内部不确定的动力学参数和未知死区进行处理。死区是一种典型的非线性特性,广泛存在于机器人系统中,尤其是机器人的关节处,会严重影响系统的跟踪精度。文献[12]针对一类具有死区的非线性系统提出了一种自适应控制方法以满足系统全局稳定性和期望的跟踪精度。本文在设计自适应控制器的过程中,对文献[12]的方法进行扩展,具体应用到机器人系统中,并且进一步考虑该机器人系统受外部干扰的情形。在式(1)的两边同时乘以
| $ \begin{array}{l} \mathit{\boldsymbol{\ddot q}} + {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) = \\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\tau }} + {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{d}} \end{array} $ | (7) |
式(7)又可以改写为:
| $ \mathit{\boldsymbol{\ddot q}} + {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{\theta }}_1} + {\mathit{\boldsymbol{Y}}_2}{\mathit{\boldsymbol{\theta }}_2} = {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\tau }} + {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{d}} $ | (8) |
式中,
| $ {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{\theta }}_1} = {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}}\;\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_2}{\mathit{\boldsymbol{\theta }}_2} = {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}})} \end{array} $ |
对于死区模型式(3),可以改写成如下形式[12]:
| ${\tau _i}(t) = {\rm{D}}{{\rm{Z}}_i}({v_i}(t)) = {m_{\rm e}}{v_i}(t) + {\rm{d}}{{\rm{z}}_i}({v_i}(t))$ | (9) |
式中,
| $ {\rm{d}}{{\rm{z}}_i}({v_i}(t)) = \left\{ \begin{array}{l} - {m_{\rm{e}}}{b_{{{\rm{r}}_i}}}\;\;\;\;\;\;{\rm{if}}\;\;\;\;{v_i}(t)\geqslant{b_{{{\rm{r}}_i}}}\\ - {m_{\rm{e}}}{v_i}(t)\;\;\;{\rm{if}}\;\;\;\;{b_{{{\rm{l}}_i}}} < {v_i}(t) < {b_{{{\rm{r}}_i}}}\\ - {m_{\rm{e}}}{b_{{{\rm{l}}_i}}}\;\;\;\;\;\;{\rm{if}}\;\;\;\;{v_i}(t)\leqslant{b_{{{\rm{l}}_i}}} \end{array} \right. $ |
设
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\ddot q}} + {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{\theta }}_1} + {\mathit{\boldsymbol{Y}}_2}{\mathit{\boldsymbol{\theta }}_2}{\rm{ = }}\\ {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}}){\mathit{m}_{\rm{e}}}\mathit{\boldsymbol{v}}(\mathit{t}) + {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}}){\rm{dz}}(\mathit{\boldsymbol{v}}(\mathit{t})) + {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{d}} \end{array} $ | (10) |
其中,
| $ \ \ \ \ \ \ \ \ \ \ \mathit{\boldsymbol{v}}(t) = {[{v_1}(t),{v_2}(t),...,{v_n}(t)]^{\rm{T}}}\\ {\rm{dz}}(\mathit{\boldsymbol{v}}(t)) = {[{\rm{d}}{{\rm{z}}_1}({v_1}(t)),{\rm{d}}{{\rm{z}}_2}({v_2}(t)), \cdots ,{\rm{d}}{{\rm{z}}_n}({v_n}(t))]^{\rm{T}}} $ |
对于机器人系统式(1),此时可选择其状态变量为
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\int {\Delta \mathit{\boldsymbol{x}}(t){\rm{d}}t} + \Delta \mathit{\boldsymbol{\dot q}} $ | (11) |
式中,
| $\mathit{\boldsymbol{\dot s }}= \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \Delta \mathit{\boldsymbol{x}} + \mathit{\boldsymbol{\ddot q}} - {\mathit{\boldsymbol{\ddot q}}_{\rm d}}$ | (12) |
再将式(10)代入式(12)得:
| $ \mathit{\boldsymbol{\dot s }} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \Delta \mathit{\boldsymbol{x}}(t) - {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{\theta}} _1} - {\mathit{\boldsymbol{Y}}_2}{\mathit{\boldsymbol{\theta}} _2}{\rm{ + }}{\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}}){m_{\rm e}}\mathit{\boldsymbol{v}}(t){\rm{ + }}\\ \ \ \ \ {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}}){\rm{dz}}({\bf{v}}(t)){\rm{ + }}{\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{d}} - {\mathit{\boldsymbol{\ddot q}}_{\rm d}} $ | (13) |
在引入控制律之前,还需要定义以下一些变量:
| $\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{s}}^\prime } = \mathit{\boldsymbol{s}} - \varepsilon {\rm{sat}}\left( {\frac{\mathit{\boldsymbol{s}}}{\varepsilon }} \right)}\\ {\phi {\rm{ = }}\frac{1}{{{m_{\text{e}}}}},\;\;\;\;\mathit{\boldsymbol{\theta }}{\rm{ = }}\frac{1}{{{m_{\text{e}}}}}{{[{\mathit{\boldsymbol{\theta }}_1},{\mathit{\boldsymbol{\theta }}_2}]}^{\rm{T}}}}\\ {\mathit{\boldsymbol{E}}{\rm{ = }}\mathit{\boldsymbol{\ddot q}}{}_{\text{d}} - \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\Delta \mathit{\boldsymbol{x,}}\;\;\;\mathit{\boldsymbol{Y}}{\rm{ = }}\frac{1}{{{m_{\text{e}}}}}[{\mathit{\boldsymbol{Y}}_1},{\mathit{\boldsymbol{Y}}_2}]}\\ {{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{Y}}}{\rm{ = }}(\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}}))\mathit{\boldsymbol{Y}},{\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{E}}}{\rm{ = }}(\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}}))\mathit{\boldsymbol{E}}} \end{array} $ |
式中,
控制律为:
| $ \mathit{\boldsymbol{v}}(t) = - \mathit{\boldsymbol{Ks}} + \hat \phi \mathit{\boldsymbol{E}} + \mathit{\boldsymbol{Y\hat \theta }} - {\mathit{\boldsymbol{K}}^*}{\rm{sat}}\left( {\frac{\mathit{\boldsymbol{s}}}{\varepsilon }} \right) - \mathit{\boldsymbol{\hat d}} - {\mathit{\boldsymbol{F}}^{ - 1}}(\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot {\hat d}}} $ | (14) |
式中,
动力学参数自适应律为:
| $\mathit{\boldsymbol{\hat \theta }} = - \mathit{\boldsymbol{\varGamma}} \mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{Y}}}^{\rm{T}}\mathit{\boldsymbol{s}}'$ | (15) |
死区参数自适应律为:
| $\hat \phi = - \eta \mathit{\boldsymbol{W}}_{\mathit{\boldsymbol{E}}}^{\rm{T}}\mathit{\boldsymbol{s}}'$ | (16) |
式中,
将式(14)代入式(13),并利用干扰观测误差的动力学式(5),得到机器人系统的闭环方程为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\dot s}} = - \mathit{\boldsymbol{E}} - {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{\theta }}_1} - {\mathit{\boldsymbol{Y}}_\mathit{\boldsymbol{2}}}{\mathit{\boldsymbol{\theta }}_2} + {\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}}){m_{\text{e}}}{\rm{ + }}\\ \left[ { - \mathit{\boldsymbol{Ks}} + \hat \phi \mathit{\boldsymbol{E}} + \mathit{\boldsymbol{Y\hat \theta }} - {\mathit{\boldsymbol{K}}^*}{\rm{sat}}\left( {\frac{\mathit{\boldsymbol{s}}}{\varepsilon }} \right)} \right]{\rm{ + }}{\mathit{\boldsymbol{M}}^{ - 1}}(\mathit{\boldsymbol{q}}){\rm{dz}}(\mathit{\boldsymbol{v}}(t)) \end{array} $ | (17) |
定理1 考虑非线性机器人系统式(1)同时受外部干扰、部动力学参数不确定性、未知死区特性的影响,如果通过干扰观测器式(4)、自适应控制器式(14)~式(16)进行控制,则信号
证明:考虑如下李亚普诺夫函数:
| $V = \frac{1}{{2{m_{\rm e}}}}{\mathit{\boldsymbol{s}}'^{\rm{T}}}\mathit{\boldsymbol{Ms}}' + \frac{1}{2}\Delta {\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}\Delta \mathit{\boldsymbol{\theta }} + \frac{1}{{2\eta }}\Delta {\phi ^2}$ | (18) |
式中,
| $ \dot V = \frac{1}{{{m_{\rm e}}}}{\mathit{\boldsymbol{s}}'^{\rm{T}}}\mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\dot s }} + \Delta {\mathit{\boldsymbol{\theta }} ^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}\mathit{\boldsymbol{\dot {\hat \theta}}} + \frac{1}{\eta }\Delta \phi \dot {\hat \phi} + \frac{1}{{2{m_{\rm e}}}}{\mathit{\boldsymbol{s}}'^{\rm{T}}}\mathit{\boldsymbol{\dot Ms}}' $ | (19) |
再将式(15)~式(17)代入式(19)得:
| $ \dot V = - {\mathit{\boldsymbol{s}}'^{\rm{T}}}\mathit{\boldsymbol{Ks}} - {\mathit{\boldsymbol{s}}'^{\rm{T}}}(t){\mathit{\boldsymbol{K}}^*}{\rm{sat}}\left( {\frac{\mathit{\boldsymbol{s}}}{\varepsilon }} \right) + {\mathit{\boldsymbol{s}}'^{\rm{T}}}\frac{{{\rm{dz}}(\mathit{\boldsymbol{v}}(t))}}{{{m_e}}}{\rm{ + }}\\ \ \ \ \ \ \ \ \ \ \frac{1}{{2{m_{\rm e}}}}{\mathit{\boldsymbol{s}}'^{\rm{T}}}\mathit{\boldsymbol{\dot M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{s}}' $ | (20) |
再根据
| $ \begin{array}{l} \dot V(t) = - {{\mathit{\boldsymbol{s'}}}^{\rm{T}}}\mathit{\boldsymbol{Ks'}} - {{\mathit{\boldsymbol{s'}}}^{\rm{T}}}(\mathit{\boldsymbol{K}}\varepsilon + {\mathit{\boldsymbol{K}}^*}){\rm{sat}}\left( {\frac{\mathit{\boldsymbol{s}}}{\varepsilon }} \right){\rm{ + }}{{\mathit{\boldsymbol{s'}}}^{\rm{T}}}\frac{{{\rm{dz}}(\mathit{\boldsymbol{v}}(t))}}{{{m_{\text{e}}}}} + \\ \;\;\;\;\;\;\frac{1}{{2{m_{\text{e}}}}}{{\mathit{\boldsymbol{s'}}}^{\rm{T}}}\mathit{\boldsymbol{\dot M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{s'}} \le - {{\mathit{\boldsymbol{s'}}}^{\rm{T}}}\mathit{\boldsymbol{Ks'}} - {\rm{ei}}{{\rm{g}}_{\min }}(\mathit{\boldsymbol{K}}\varepsilon ).\left\| {{{\mathit{\boldsymbol{s'}}}^{\rm{T}}}} \right\| - \\ \;\;\;\;\;\;\;\;\;\left[ {{\rm{ei}}{{\rm{g}}_{\min }}({\mathit{\boldsymbol{K}}^*}) - \frac{{\left\| {{\rm{dz}}(\mathit{\boldsymbol{v}}(t))} \right\|}}{{{m_{\text{e}}}}} - \frac{{\left\| {\mathit{\boldsymbol{\dot M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{s'}}} \right\|}}{{2{m_{\text{e}}}}}} \right] \cdot \left\| {{{\mathit{\boldsymbol{s'}}}^{\rm{T}}}} \right\| \end{array} $ | (21) |
由于
| $\dot V \leqslant - {\mathit{\boldsymbol{s}}'^{\rm{T}}}\mathit{\boldsymbol{Ks}}' \leqslant 0$ | (22) |
因此
| $ {\rm{ei}}{{\rm{g}}_{\min }}(\mathit{\boldsymbol{K}}){\mathit{\boldsymbol{s}}'^{\rm{T}}}\mathit{\boldsymbol{s}}' \leqslant \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{s}}'^{\rm{T}}}\mathit{\boldsymbol{s}}' \leqslant - \dot V $ | (23) |
对式(23)两边同时积分可以得到:
| $\begin{gathered} {\rm{ei}}{{\rm{g}}_{\min }}(\mathit{\boldsymbol{K}})\int_{{\rm{ }}0}^{{\rm{ }}t} {{{\left\| {\mathit{\boldsymbol{s}}'} \right\|}^2}} {\rm{d}}t \leqslant - \int_{{\rm{ }}0}^{{\rm{ }}t} {\dot V} {\rm{d}}t = \\ \ \ \ \ \ V(0) - V(t) \leqslant V(0) < \infty \\ \end{gathered} $ | (24) |
因此,
把设计的基于干扰观测器的自适应控制方法在1-DOF单连杆的机器人系统中进行仿真,结构如图 2所示[14]。
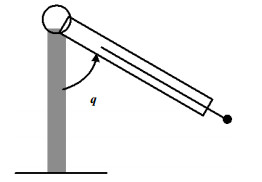 |
| 图2 单连杆机器人结构 |
该机器人的转动惯量为
在仿真过程中,还将本文所设计的基于干扰观测器的自适应控制器的效果与无干扰观测器的自适应控制效果进行了比较,无干扰观测器的自适应控制器为:
| $\mathit{\boldsymbol{v}}(t) = - \mathit{\boldsymbol{Ks}} + \hat \phi \mathit{\boldsymbol{E}} + \mathit{\boldsymbol{Y\hat \theta}} - {\mathit{\boldsymbol{K}}^*}{\rm{sat}}\left( {\frac{\mathit{\boldsymbol{s}}}{\varepsilon }} \right)$ | (25) |
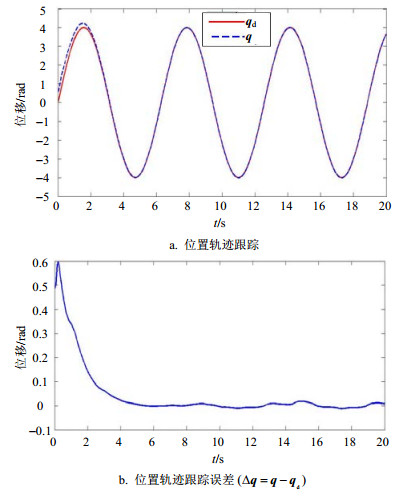 |
| 图3 无干扰观测器的自适应控制效果 |
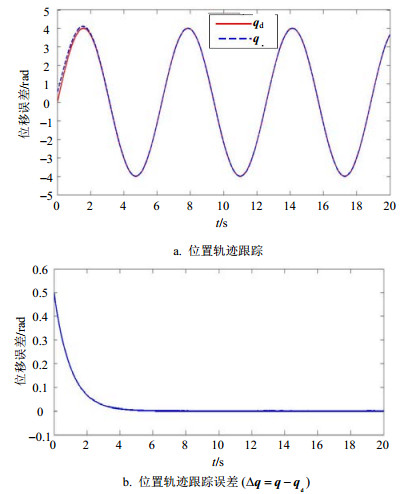 |
| 图4 基于干扰观测器的自适应控制效果 |
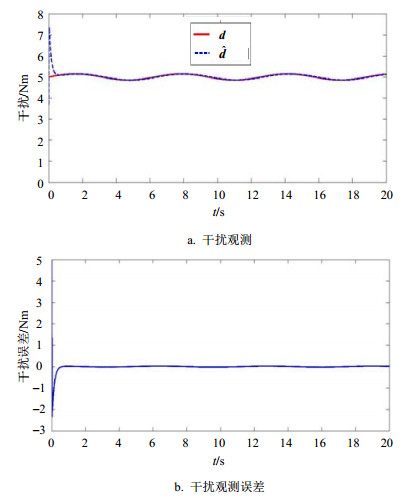 |
| 图5 干扰观测器效果 |
从图 4可以看到,采用本文所设计的基于干扰观测器的自适应控制器,机器人的位置
本文针对同时受到外部干扰、内部动力学参数不确定性和未知死区特性的遥操作系统,提出了一种基于干扰观测器的自适应控制方案。所设计方法的有效性通过数学推导和数值仿真得到证明和验证。在此基础上,如何考虑其他更为复杂的非线性因素如齿隙、磁滞等,从而系统地形成一套不确定性机器人系统基于干扰观测器的自适应控制算法将作为下一步的研究内容。
| [1] |
刘金琨.
机器人控制系统的设计与MATLAB仿真[M]. 北京: 清华大学出版社, 2008.
LIU Jin-kun. Design and MATLAB simulations of robotic control systems[M]. Beijing: Tsinghua University Press, 2008. |
| [2] |
CRAIG J J, HSU P, SASTRY S S. Adaptive control of mechanical manipulators[J].
The International Journal of Robotics Research, 1987, 6(2): 16–28.
DOI:10.1177/027836498700600202 |
| [3] |
SLOTINE J J E, LI W. On the adaptive control of robot manipulators[J].
The International Journal of Robotics Research, 1987, 6(3): 49–59.
|
| [4] |
SPONG M W, ORTEGA R. On adaptive inverse dynamics control of rigid robots[J].
IEEE Transactions on Automatic Control, 1990, 35(1): 92–95.
DOI:10.1109/9.45152 |
| [5] |
CHEAH C C, LIU C, SLOTINE J J E. Adaptive tracking control for robots with unknown kinematic and dynamic properties[J].
The International Journal of Robotics Research, 2006, 25(3): 283–296.
DOI:10.1177/0278364906063830 |
| [6] |
HUNG N V Q, TUAN H D, NARIKIYO T, et al. Adaptive control for nonlinearly parameterized uncertainties in robot[J].
IEEE transactions on control systems technology, 2008, 16(3): 458–468.
DOI:10.1109/TCST.2007.903088 |
| [7] |
CHEN W H, BALANCE D J, GAWTHROP P J, et al. A nonlinear disturbance observer for robotic manipulators[J].
IEEE Transactions on Industrial Electronics, 2000, 47(4): 932–938.
DOI:10.1109/41.857974 |
| [8] |
NIKOOBIN A, HAGHIGHI R. Lyapunov-based nonlinear disturbance observer for serial n-link robot manipulators[J].
IEEE Transactions on Industrial Electronics, 2009, 55(2-3): 135–153.
|
| [9] |
刘霞, 黄琦, 陈勇. 不确定遥操作系统带干扰观测器的自适应控制[J].
控制理论与应用, 2012, 29(5): 681–687.
LIU Xia, HUANG Qi, CHEN Yong. Adaptive control of uncertain teleoperation systems with disturbance observer[J]. Control Theory & Applications, 2012, 29(5): 681–687. |
| [10] |
KELLY R, SANTIBANEZ V, LORIA A.
Control of robot manipulators in joint space[M]. Berlin, Germany: Springer, 2005.
|
| [11] |
TAO G, KOKOTOVIC P V.
Adaptive control of systems with actuator and sensor nonlinearities[M]. New York: Wiley, 1996.
|
| [12] |
WANG X, SU C, HONG H. Robust adaptive control of a class of nonlinear systems with unknown dead-zone[J].
Automatica, 2004, 40(3): 407–413.
DOI:10.1016/j.automatica.2003.10.021 |
| [13] |
SLOTINE J J E, LI W.
Applied Nonlinear Control[M]. Englewood Cliffs, USA: Prentice-Hall, 1991.
|
| [14] |
CRRADINI M L, ORLANDO G, PARLANGELI G. A VSC approach for the robust stabilization of nonlinear plants with uncertain nonsmooth actuator nonlinearities-a unified framework[J].
IEEE Transactions on Automatic Control, 2004, 49(5): 807–812.
DOI:10.1109/TAC.2004.828324 |
 2015, Vol. 44
2015, Vol. 44
