近年来,非线性理论在电路与系统的研究中获得了广泛的应用。电力电子电路中的开关变换器是非线性变结构控制系统,具有复杂的非线性行为,如倍周期分岔、Hopf分岔、Flip分岔、边界碰撞分岔等多种通向混沌的分岔道路、次谐波振荡、降频和低频波动现象等[1-8]。
峰值电流控制因其优良的性能在工业界得到了广泛的应用。文献[9]研究了采用斜坡补偿改善开关变换器稳定性的机理。文献[10]得到了Boost变换器轨道状态发生转移时的分界线方程,通过引入适当的斜坡补偿实现系统的混沌镇定控制。文献[11]在反馈电路中引入斜坡补偿使开关变换器的工作模式从断续导电模式转移到连续导电模式,实现了系统工作模式的转移,避免弱混沌强阵发现象的出现。文献[12]系统地研究了二阶变换器斜坡补偿的混沌镇定控制和工作模式转移的动力学机理。
本文对峰值电流控制的同步开关Boost变换器进行了深入的研究,为了研究电感电流的放电斜率对系统稳定性的影响,在反馈回路中不加斜坡补偿电流,通过改变受控电压源的强度来改变电感电流的放电斜率,从而改变同步开关Boost变换器电感电流的分岔和混沌状态,实现周期轨道的移动。
1 峰值电流控制同步开关Boost变换器峰值电流控制同步开关Boost变换器的原理图如图 1所示。该电路采用同步开关管进行控制,二极管被MOSFET代替(高端开关),主开关管是低端开关。图中E为输入电压,Q1、Q2分别为高端开关管、低端开关管,L为电感,C为滤波电容,R为负载电阻。iL为电感L上流过的电流,vo为负载电阻R两端的电压,Vs为受控电压源。当时钟脉冲CLK开始工作时,低端开关管Q2导通,高端开关管Q1关断,电感电流iL线性上升,当电感电流iL增加至参考电流Iref时,比较器复位触发器,低端开关管Q2关断,高端开关管Q1导通,电感电流iL近似线性下降,直至下一个时钟脉冲开始时,低端开关管Q2再次导通,高端开关管Q1再次关断。
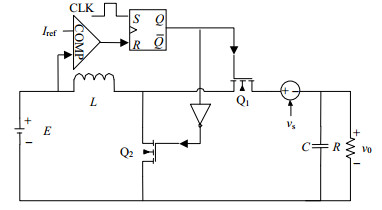 |
| 图1 峰值电流控制同步开关Boost变换器 |
基于峰值电流控制同步开关Boost变换器的工作原理,系统工作于CCM模式,电路存在两种工作状态,即低端开关管导通电感电流上升阶段和低端开关管关断电感电流下降阶段。同步开关Boost变换器的状态方程为:
| $\mathit{\boldsymbol{\dot{x}}} = {\mathit{\boldsymbol{A}}_1}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{B}}_1}E$ | (1) |
| $\mathit{\boldsymbol{\dot{x}}} = {\mathit{\boldsymbol{A}}_2}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{B}}_2}E - G{V_{\rm{s}}}$ | (2) |
式中,
| $ {\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} 0&0 \\ 0&{ - 1/RC} \end{array}} \right]\\ {\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} 0&{ - 1/L} \\ {1/C}&{ - 1/RC} \end{array}} \right]\\ {\mathit{\boldsymbol{B}}_1} = {\mathit{\boldsymbol{B}}_2} = \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {1/L} \\ 0 \end{array}} \right] $ |
由式(2)可知,
| $\left\{ \begin{array}{l} {i_{n + 1}} = {{\rm{e}}^{\alpha {t_n}^\prime }}({C_1}\sin (\omega {t_n}^\prime ) + {C_2}\cos (\omega {t_n}^\prime )) + \frac{E}{R} - \frac{{{V_{\rm{s}}}}}{R} \\ {v_{n + 1}} = E - {V_{\rm{s}}} + L{{\rm{e}}^{\alpha {t_n}^\prime }}[({C_2} - \omega {C_1})\cos (\omega {t_n}^\prime ) + \\ \quad \quad \;({C_1} + \omega {C_2})\sin (\omega {t_n}^\prime )] \end{array}\right.$ | (3) |
式中
当同步开关Boost变换器的时钟周期足够小时,则开关管的导通时间tn趋近于零。在此情况下,式(3)中的非线性项
系统在稳定点X的判定式[13]为:
| $\Delta {x_{n + 1}} = \sum\limits_{k = 1}^\infty {{{\left. {\left( {\frac{1}{{k!}}\frac{{{\partial ^k}f(x)}}{{\partial {x^k}}}} \right)} \right|}_{x = X}}(} \Delta {x_n}{)^k}$ | (4) |
式中,
当系统的扰动Δxn很小时,式(4)中的高阶项很小,可以忽略不计,可得系统的稳定性判据为:
| $ \left| {\frac{{\partial {i_{n + 1}}}}{{\partial {i_n}}}} \right| = {\left| {\frac{{\partial f(x)}}{{\partial x}}} \right|_{x = X}} = \left| { - \frac{{L({I_{{\rm{ref}}}} - E/R + {V_{\rm{s}}}/R)}}{{2RCE}}} \right| \leqslant 1 $ | (5) |
由式(5)可得系统在临界点处电感电流为:
| ${I_{{\rm{refs}}}} = - \frac{1}{R}{V_{\rm{s}}} + \frac{E}{R} + \frac{{2RCE}}{L}$ | (6) |
由式(6)可以反映出系统首次分岔点的电感电流值Irefs随着Vs的增大而减小,所以Vs的值越大,首次分岔点的Iref值越小,系统的稳定性越差。
3 数值仿真当同步开关Boost变换器的电路参数发生变化时,系统具有非常复杂的非线性动力学行为。当系统反馈回路中参考电流没有进行斜坡补偿时,变换器的电路参数分别为E=5 V,T=200 μs,L=1 mH,C=15 μF,R=20 Ω。以同步开关Boost变换器反馈回路中参考电流Iref为分岔参数,变换器电感电流的分岔图如图 2所示。当受控电压源Vs的值为0 V时,从图 2中可以发现,参考电流Iref在0.6~1.6 A之间变化时,系统经历分岔到混沌,在Iref=0.762 A时系统发生第一次倍周期分岔。当Iref=1.224 A时,系统发生周期3分岔。随着参考电流Iref的继续增大,系统发生周期6分岔,最后系统进入混沌态。
 |
| 图2 以参考电流Iref为分岔参数同步开关Boost变换器电感电流的分岔图 |
通过对比图 2中数值仿真的结果发现,加入受控电压源Vs前后,系统的稳定性发生了巨大的变化,在加入直流电压源Vs前参考电流Iref在0.6~0.762 A之间变化时系统是稳定的,系统处于周期1状态,但是在加入受控电压源Vs后系统的稳定性变差了,即参考电流Iref在0.689 A时就进入周期2状态,从李雅普诺夫稳定性理论可知,系统处于不稳定状态。同时,系统发生周期3分岔的分岔点也大大地提前了,即参考电流Iref=1.125 A时系统就进入周期3状态。因此同步开关Boost变换器加入受控电压源后比加入前提前结束周期1状态,进入分岔状态,从而验证了系统稳定性分析中式(6)所示的首次分岔点与受控电压源Vs强度之间的关系,说明通过改变受控电压源Vs的强度可以减小系统的稳态区域。
4 电路仿真和实验验证以一个峰值电流控制同步开关Boost变换器为例,在反馈回路中的参考电流Iref未加入斜坡补偿,在高端开关管后面串联一个受控电压源Vs,进行电路仿真和实验验证。根据前面的理论分析,通过改变受控电压源Vs的值来改变电感电流的放电斜率,使得系统的稳态范围变小,同时使系统提前进入混沌区域,影响系统的动力学特性。
峰值电流控制同步开关Boost变换器的电路参数采用上述数值仿真时选择的电路参数。图 3和图 4分别为参考电流Iref=0.713 A时同步开关Boost变换器的电路仿真结果和实验结果。对比图 3和图 4的结果可知,当受控电压源Vs为0 V时,系统工作于周期1状态。当受控电压源Vs为2 V时,电感电流的时域波形中出现了二次谐波振荡现象,开关管的驱动波形中出现两种频率信号,其相图中出现了二分环,表明系统工作于周期2状态。图 5和图 6分别为参考电流Iref=1.17 A时同步开关Boost变换器的电路仿真结果和实验结果。对比图 5和图 6的结果可知,当受控电压源Vs为0 V时,系统工作于周期2状态。当受控电压源Vs为2 V时,系统工作于周期3状态。所以,电路仿真和实验结果与基于系统离散模型所得到的数值仿真结果完全一致,从而验证了理论分析的正确性。在实际的电路中,由于功率开关管和二极管都存在导通电阻,会产生一定的电压降,这些电压降会严重影响系统的动力学特性。在实际电路稳定性设计和元器件选择时,要慎重考虑功率开关管或者二极管导通时的电压降对系统稳定性的影响,对于实际的电路设计具有重要的理论指导意义。
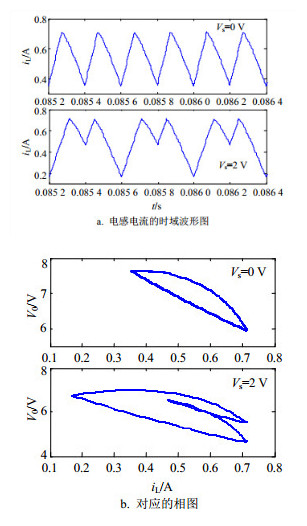 |
| 图3 当Iref =0.713 A时同步开关Boost变换器的电路仿真结果 |
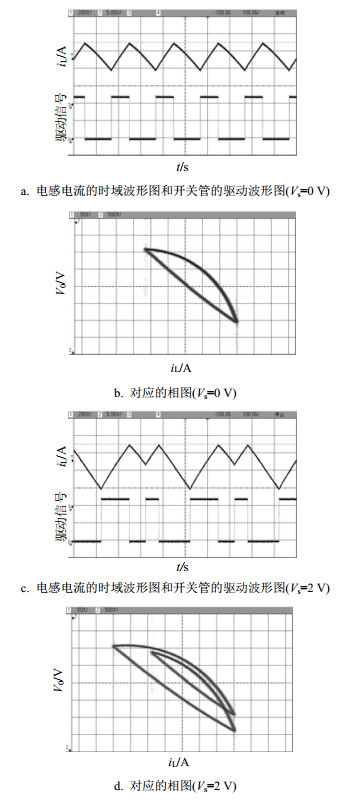 |
| 图4 当Iref =0.713 A时同步开关Boost变换器的实验结果 |
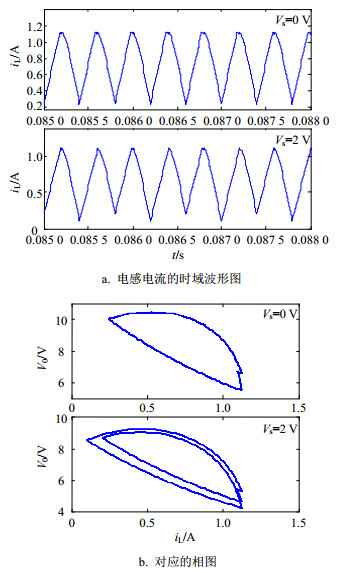 |
| 图5 当Iref=1.17 A时同步开关Boost变换器的电路仿真结果 |
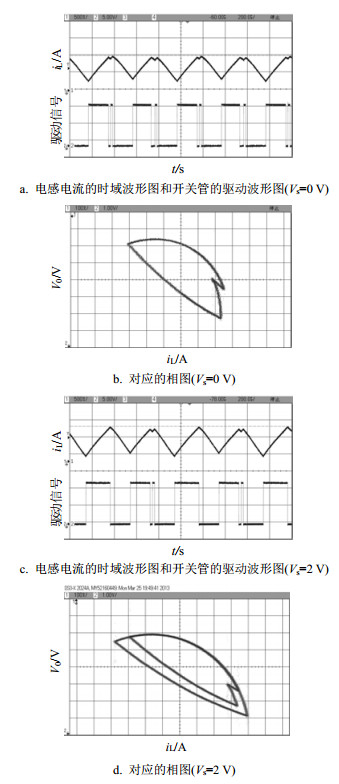 |
| 图6 当Iref=1.17 A时同步开关Boost变换器的实验结果 |
本文以峰值电流控制同步开关Boost变换器为研究对象,考虑反馈回路中未加入斜坡补偿,分析受控电压源对电感电流放电斜率的改变,进而影响系统动力学行为的机理。研究结果表明,在峰值电流控制同步开关Boost变换器中加入受控电压源可以改变电感电流的放电斜率,进而影响系统的稳定性,当增加受控电压源的值时,系统的稳定区域被大大地缩减了。所以在实际开关变换器的设计时要充分考虑功率开关管或者二极管上的压降对系统稳定性的影响,为工程人员提供理论依据,具有重要的实用价值。
| [1] |
GIAOURIS D, BANERJEE S, IMRAYED O, et al. Complex interaction between tori and onset of three-frequency quasi-periodicity in a current mode controlled Boost converter[J].
IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2012, 59(1): 207–214.
DOI:10.1109/TCSI.2011.2161371 |
| [2] |
BAO B, ZHOU G, XU J, et al. Unified classification of operation-state regions for switching converters with ramp compensation[J].
IEEE Transactions on Power Electronics, 2011, 26(7): 1968–1975.
DOI:10.1109/TPEL.2010.2098421 |
| [3] |
WANG J, BAO B, XU J, et al. Dynamical effects of equivalent series resistance of output capacitor in constant on-time controlled Buck converter[J].
IEEE Transactions on Industrial Electronics, 2013, 60(5): 1759–1768.
DOI:10.1109/TIE.2012.2190956 |
| [4] |
MANDAL K, BANERJEE S, CHAKRABORTY C, et al. Bifurcations in frequency controlled load resonant DC-DC converters[C]//2012 IEEE International Symposium on Circuits and Systems. [S. l. ]: IEEE, 2012: 1135-1138.
|
| [5] |
YESODHA V, KAVIPRIYA R, JOSHNA T S, et al. Analysis of chaos and bifurcation in DC-DC converter using matlab[C]//2013 International Conference on Circuits, Power and Computing Technologies. [S. l. ]: [s. n. ], 2013: 481-487.
|
| [6] |
MANDA K, BANERJEE S, CHAKRABORTY C. Symmetry-breaking bifurcation in load resonant DC-DC converters[C]//2011 IEEE International Symposium on Circuits and Systems. [S. l. ]: IEEE, 2011: 1327-1330.
|
| [7] |
MANDA K, BANERJEE S, CHAKRABORTY C. Symmetry-breaking bifurcation in series-parallel load resonant DC-DC converters[J].
IEEE Transactions on Circuits and Systems Ⅰ: Regular Papers, 2013, 60(3): 778–787.
DOI:10.1109/TCSI.2012.2209732 |
| [8] |
MORENO-FONT V, BENADERO L, EL-AROUDI A. Non-smooth bifurcations in a 1-D piecewise linear model of a single inductor two-output DC-DC switching converter[C]//2011 IEEE International Symposium on Circuits and Systems. [S. l. ]: IEEE, 2011: 2725-2728.
|
| [9] |
包伯成, 许建平, 刘中. 开关DC-DC变换器斜坡补偿的稳定性控制研究[J].
电子科技大学学报, 2008, 37(3): 397–400.
BAO Bo-cheng, XU Jian-ping, LIU Zhong. Study on stability control of ramp compensation for switched DC-DC converter[J]. Journal of University of Electronic Science and Technology of China, 2008, 37(3): 397–400. |
| [10] |
包伯成, 许建平, 刘中. 具有两个边界的Boost变换器分岔行为和斜坡补偿的镇定控制[J].
物理学报, 2009, 58(5): 2949–2956.
BAO Bo-cheng, XU Jian-ping, LIU Zhong. Bifurcation of Boost converter with two boundaries and its stability control by ramp compensation[J]. Acta Physica Sinica, 2009, 58(5): 2949–2956. DOI:10.7498/aps.58.2949 |
| [11] |
包伯成, 周国华, 许建平, 等. 斜坡补偿电流模式控制开关变换器的动力学建模与分析[J].
物理学报, 2010, 59(6): 3769–3777.
BAO Bo-cheng, ZHOU Guo-hua, XU Jian-ping, et al. Dynamical modeling and analysis of current mode controlled switching converter with ramp compensation[J]. Acta Physica Sinica, 2010, 59(6): 3769–3777. DOI:10.7498/aps.59.3769 |
| [12] |
杨平, 包伯成, 沙金, 等. 开关变换器斜坡补偿动力学机理研究[J].
物理学报, 2013, 62(1): 010504.
YANG Ping, BAO Bo-cheng, SHA Jin, et al. Dynamical mechanism of ramp compensation for switching converter[J]. Acta Physica Sinica, 2013, 62(1): 010504. |
| [13] |
张波, 曲颖. Buck DC/DC变换器分岔和混沌的精确离散模型及实验研究[J].
中国电机工程学报, 2003, 23(12): 99–103.
ZHANG Bo, QU Ying. Study on the experiment and the precise discrete model of bifurcation and chaos for buck DC/DC converter[J]. Proceedings of the CSEE, 2003, 23(12): 99–103. DOI:10.3321/j.issn:0258-8013.2003.12.020 |
 2015, Vol. 44
2015, Vol. 44
