2. 西南科技大学核废物与环境安全国防重点学科实验室 四川 绵阳 621010;
3. 西南科技大学信息工程学院 四川 绵阳 621010;
4. 西南科技大学特殊环境机器人技术四川省重点实验室 四川 绵阳 621010
2. Fundamental Science on Nuclear Wastes and Environmental Safety Laboratory, Southwest University of Science and Technology Mianyang Sichuan 621010;
3. School of Information and Engineering, Southwest University of Science and Technology Mianyang Sichuan 621010;
4. Robot Technology Used for Special Environment Key Laboratory of Sichuan Province, Southwest University of Science and Technology Mianyang Sichuan 621010
图像质量评价方法在视觉处理算法中扮演着重要角色,具有重要的应用价值。人是图像信号的最终接收者,最直观、最符合HVS的图像质量评价方法是主观测试评价,最常用的主观图像质量评价方法是平均意见打分(mean opinion score,MOS)方法。然而,该方法代价昂贵且费时,在实际图像处理应用中不太实用。主观图像质量评价方法的不足,促使研究人员在自动计算图像主观视觉质量的评价方法方面开展了大量研究工作[1-8]。
根据不同的图像质量评价方法,图像质量评价标准可分为两大类:基于HVS特性建模方法和图像信号驱动方法[1]。
基于HVS特性建模方法综合相关心理学属性和生理学知识,包括时间、空间、色彩空间分解、对比度敏感函数(contrast sensitivity function,CSF)、亮度自适应以及掩模效果等[1],采用系统建模方法,建立图像质量评价模型。近年来,许多基于HVS的图像质量评价方法[2-3]被提出,其中一些方法也考虑了最小可觉差(just noticeable distortion,JND)模型[4-5]。视觉心理学中的视觉模型被应用到基于HVS的图像质量评价方法中,效果较好。但该类评价方法计算量大,且视觉机理研究与实际工程建模不匹配[1],导致这类方法的应用有局限性。
近年来,基于信号驱动的图像质量评价方法受到广泛关注。该类评价方法基于图像信号的提取与分析,比如统计特征、结构、亮度失真等[6-8]。信号驱动方法不是为了图像质量评价而试图去建立复杂的HVS模型,而是重点关注如何表达图像特征以估计图像整体质量。该类方法通常也会考虑图像内容和失真分析的心理学效应。然而,虽然一些图像保真度模型能够反应图像质量的变化,但由于一些缺陷[1],该类评价方法并不能表达HVS的主观感受。例如,并不是每一个图像的变化都容易被觉察,也不一定导致失真。因此,信号驱动的图像质量评价方法需引入HVS特性来弥补这些不足,从而更加逼近人眼主观感受。
1 全变分模型变分方法已被广泛应用于图像处理和计算机视觉领域[9]。由文献[10]提出的TV模型是图像处理中最成功的偏微分方程(partial differential equation,PDE)模型之一。全变分可描述为:
| ${\rm{TV}}(u) = \int_{\mathit{\Omega } } {\left| {\nabla u} \right|} $ | (1) |
式中,
文献[9-10]表明,TV范数描述图像最合适。TV范数本质上是
本文提出的基于TV模型的PIQA方法,将重点考虑图像结构和图像封闭区域亮度变化。与其他图像质量评价方法相比,最大的区别是引入了TV模型来评价图像在空间域的结构变化,同时也考虑了图像中封闭区域的亮度变化。
2 基于全变分模型的图像质量评价 2.1 基于TV模型的图像质量评价框架通过HVS观测自然图像时,有许多因素影响图像质量。其中,有两种重要因素值得考虑:1)图像边缘结构信息;2)亮度信息[11]。基于此,本文提出一种新的基于TV模型的PIQA (TVPIQA)方法。
基于TV模型的图像质量评价框架如图 1所示。
| ${\rm{TVPIQA}} = \frac{{{\mu _1} + {\mu _2}}}{2}$ | (2) |
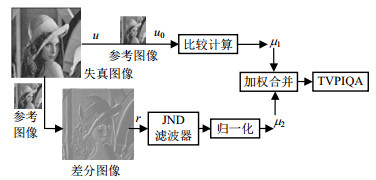 |
| 图1 基于TV模型的图像质量评价框架 |
由于TV范数适合描述图像的不连贯性,因此,图像结构信息的改变可由参考图像与失真图像之间全变分的改变量来衡量:
| ${\rm{T}}{{\rm{V}}_{{\rm{struct}}}} = {\left\| {{\rm{TV}}(u) - {\rm{TV}}({u_0})} \right\|_1}$ | (3) |
式中,
| ${\rm{TV}}(u) = \sum\limits_{(i,j) \in \mathit{\Omega } } {(\sqrt {{{({u_{i,j}} - {u_{i + 1,j}})}^2} + {{({u_{i,j}} - {u_{i,j + 1}})}^2}} )} $ | (4) |
式中,
虽然式(3)能很好地评价图像结构信息的改变,但计算结果没有归一化,不能作为衡量图像质量的评价标准。考虑
| ${\mu _1} = \frac{1}{N}\sum {\frac{{2\sqrt {{{({u_{i,j}} - {u_{i + 1,j}})}^2} + {{({u_{i,j}} - {u_{i,j + 1}})}^2}} \sqrt {{{({u_{0i,j}} - {u_{0i + 1,j}})}^2} + {{({u_{0i,j}} - {u_{0i,j + 1}})}^2}} + c}}{{{{({u_{i,j}} - {u_{i + 1,j}})}^2} + {{({u_{i,j}} - {u_{i,j + 1}})}^2} + {{({u_{0i,j}} - {u_{0i + 1,j}})}^2} + {{({u_{0i,j}} - {u_{0i,j + 1}})}^2} + c}}} $ | (5) |
式中,
差分图像
| ${E_r} = \frac{1}{N}\sum\limits_{(i,j) \in \mathit{\Omega } '} {r_{i,j}^2} $ | (6) |
式中,
| ${E'_r} = \frac{1}{N}\sum\limits_{(i,j) \in \mathit{\Omega } } {({r_{i,j}}{r_{i + 1,j}} + {r_{i,j}}{r_{i,j + 1}})} $ | (7) |
考虑到HVS对亮度的对比度而不是亮度的绝对值敏感,根据差分图像的平均亮度调整
| $ {E'_r} = \frac{1}{N}\sum\limits_{(i,j) \in \mathit{\Omega } } {(({r_{i,j}} - \bar r)({r_{i + 1,j}} - \bar r) + ({r_{i,j}} - \bar r)({r_{i,j + 1}} - \bar r))} $ | (8) |
式中,
为获得归一化的亮度改变量,需根据参考图像找到能量变化最大的差分图像。假设图像的能量是连续的,当图像中所有像素亮度值等于参考图像的平均亮度值时,相对于原始参考图像,图像亮度改变量最大。基于该假设,定义
| ${\mu _2} = 1 - \sqrt {\frac{{{{E'}_r}}}{{{{E'}_{{r_{\max }}}}}}} $ | (9) |
式中,
为验证TVPIQA方法的有效性,对比了目前7种主流的图像质量评价标准。其中,峰值信号噪声比(peak signal to noise ratio, PSNR)是一种广泛应用于图像处理领域的图像质量评价标准,也是一种有用的基准参照(Benchmark)。结构相似度测量指数(structural similarity index measurement, SSIM),多尺度结构相似度测量指数[12](multi-scale SSIM, MS-SSIM),小波视觉信号噪声比[13](wavelet-based visual signal to noise ratio, VSNR)和视觉信息保真度[14](visual information fidelity, VIF)等评价标准是目前公认的主流图像质量评价标准。基于信息内容权重的PSNR(information content weighted PSNR, IW-PSNR)和基于信息内容权重的SSIM(IW-SSIM)是公认的最受好评的图像质量评价标准。图像数据库采用公认的权威数据库(Cornell- A57[13],IVC[15]和TID2008[16])验证上述图像质量评价标准。
Cornell-A57数据库是由Cornell University创建,由54幅6种类型失真图像构成,失真主要包括量化失真、噪声和模糊。IVC数据库由10幅原始图像经过4种失真类型生成185幅失真图像,主要失真类型包括:1) JPEG压缩;2) JPEG2000压缩;3)局部自适应分辨率(local adaptive resolution,LAR)编码;4)模糊。TID2008图像数据库包括1 700幅失真图像,这些图像由25幅参考图像经过4种不同失真水平的17种失真函数生成。在实验对比中,未考虑TID2008中的对比度改变失真图像。
为衡量图像质量评价标准的优劣,利用评价标准与人眼主观感受评价的相关性来度量。实验中,采用线性相关系数(linear correlation coefficient,LCC)、斯皮尔曼等级相关系数(spearman’s rank correlation coefficient,SRCC)、肯德尔等级相关系数(kendall’s rank correlation coefficient,KRCC)来衡量图像质量评价标准与主观评分之间的相关性。
LCC评价了预测精度,反应了图像质量评价标准与主观评分之间的线性依赖,定义为:
| ${\rm{LCC}} = \frac{{\sum\limits_{i = 1}^N {({s_i} - \bar s)({o_i} - \bar o)} }}{{\sqrt {\sum\limits_{i = 1}^N {{{({s_i} - \bar s)}^2}} } \sqrt {\sum\limits_{i = 1}^N {{{({o_i} - \bar o)}^2}} } }}$ | (10) |
式中,
SRCC衡量了数据之间的单调性[17],定义为:
| ${\rm{SRCC}} = 1 - \frac{{6\sum\limits_{i = 1}^N {d_i^2} }}{{N({N^2} - 1)}}$ | (11) |
| ${d_i} = {R_{{s_i}}} - {R_{{o_i}}}$ | (12) |
式中,
KRCC也是一种非参秩相关统计模型,定义为:
| ${\rm{KRCC}} = \frac{{{N_c} - {N_d}}}{{N(N - 1)/2}}$ | (13) |
式中,
根据上述相关性度量标准,LCC、SRCC和KRCC值越大,越接近于1,表明测试的图像质量评价标准与实际主观评价结果相关性越好,即越能反应图像的主观视觉质量。
不同图像评价标准在Cornell-A57、IVC和TID2008数据库上的测试结果如图 2所示。可看出,本文提出的TVPIQA标准的平均性能优于其他图像评价标准。
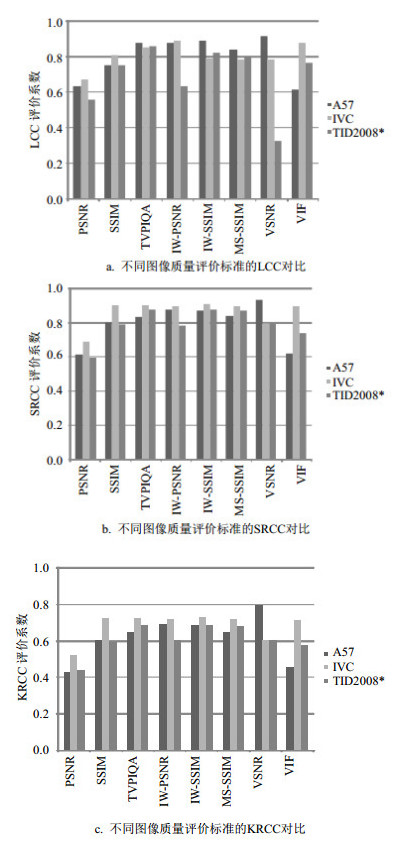 |
| 图2 不同图像评价标准在Cornell-A57,IVC和TID2008数据库上的测试结果 |
图像质量评价标准平均性能对比如表 1所示。表中给出了各个图像质量评价标准在Cornell-A57,IVC和TID2008图像数据库测试数据的LCC,SRCC和KRCC的平均值。各个相关系数平均值是以图像库大小为权重计算得到,Cornell-A57、IVC、TID2008图像库的数据权重分别为54、185、1600。
| 表1 图像质量评价标准平均性能对比 |
可看出,与其他图像质量评价标准相比,本文提出的TVPIQA标准具有较好的整体性能。值得注意的是,所提出的TVPIQA标准考虑了图像结构和能量信息,并且仅在图像空间域计算得到,不用进行变换等其他操作。
4 结论本文提出了一种基于全变分模型的空间域图像质量评价标准框架。设计的TVPIQA标准主要考虑了图像结构和亮度两种人眼视觉敏感因素,通过引入全变分模型来评价图像结构信息;同时,采用差分图像中封闭区域的能量来度量图像亮度信息的丢失程度。实验结果表明,与主观图像质量评价的相关性方面,本文提出的TVPIQA标准优于当前的主流图像质量评价标准,具有较好的综合性能。
| [1] |
LIN W, KUO C C. Perceptual visual quality metrics: a survey[J].
Journal of Visual Communication and Image Representation, 2011, 22(4): 297–312.
DOI:10.1016/j.jvcir.2011.01.005 |
| [2] |
DALY S. The visible difference predictor: an algorithm for the assessment of image fidelity[C]//Human Vision, Visual Processing, and Digital Display Ⅲ. SanJose, USA: SPIE, 1992.
|
| [3] |
FAUGERAS O D. Digital color image processing within the framework of a human visual model[J].
IEEE Trans. Acoust. Speech Signal Process, 1979, 27(4): 380–393.
DOI:10.1109/TASSP.1979.1163262 |
| [4] |
MA L, NGAN K N. Adaptive block-size transform based just noticeable difference profile for videos[C]// International Symposium on Circuits and Systems. Paris, France: IEEE, 2010.
|
| [5] |
LIN W, DONG L, XUE P. Visual distortion gauge based on discrimination of noticeable contrast changes[J].
IEEE Trans. Circuits Syst Video Technol, 2005, 5(7): 900–909.
|
| [6] |
WANG Z, BOVIK A C, SHEIKH H R, et al. Image quality assessment: from error visibility to structural similarity[J].
IEEE Trans Image Processing, 2004, 13(4): 600–612.
DOI:10.1109/TIP.2003.819861 |
| [7] |
WANG Z, LI Q. Information content weighting for perceptual image quality assessment[J].
IEEE Trans Image Processing, 2011, 20(5): 1185–1198.
DOI:10.1109/TIP.2010.2092435 |
| [8] |
AVCIBAS I, SANKUR B, SAYOOD K. Statistical evaluation of image quality measures[J].
Journal of Electronic Imaging, 2002, 11(2): 206–223.
DOI:10.1117/1.1455011 |
| [9] |
CHAN T F, SHEN J H, VESE L. Variational PDE models in image processing[J].
Notice of American Mathematical Society, 2003, 50(1): 14–26.
|
| [10] |
RUDIN L, OSHER S, FATEMI E. Nonlinear total variation based noise removal algorithms[J].
Physica D, 1992, 60: 259–268.
DOI:10.1016/0167-2789(92)90242-F |
| [11] |
NORTON T T, CORLISS D A, BAILEY J E. Psychophysical measurement of visual function[M]. [S. l. ]: Butterworth-Heinemann Press, 2002.
|
| [12] |
WANG Z, SIMONCELLI E P, BOVIK A C. Multi-scale structural similarity for image quality assessment[C]//IEEE Asilomar Conf. Signals, Syst. PacificGrove, USA: IEEE, 2003.
|
| [13] |
CHANDLER D M, HEMAMI S S. VSNR: a wavelet- based visual signal-to-noise ratio for natural images[J].
IEEE Transactions on Image Processing, 2007, 16(9): 2284–2298.
DOI:10.1109/TIP.2007.901820 |
| [14] |
SHEIKH H R, BOVIK A C. Image information and visual quality[J].
IEEE Trans Image Processing, 2006, 15(2): 430–444.
DOI:10.1109/TIP.2005.859378 |
| [15] |
NINASSI A, CALLET P, AUTRUSSEAU F. Pseudo no reference image quality metric using perceptual data hiding[C]//Human Vis Electron Imag. SanJose, USA: SPIE, 2006.
|
| [16] |
PONOMARENKO N, BATTISTI F, EGIAZARIAN K, et al. Metrics performance comparison for color image database[C]//4th International Workshop on Video Processing and Quality Metrics for Consumer Electronics. Scottsdale, USA: [s. n. ], 2009.
|
| [17] |
LARSON E C, CHANDLER D M. Most apparent distortion: Full-reference image quality assessment and the role of strategy[J].
Journal of Electronic Imaging, 2010, 19(1): 1–21.
|
 2015, Vol. 44
2015, Vol. 44
