2. 成都理工大学地球探测与信息技术教育部重点实验室 成都 610059
2. Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology Chengdu 610059
图像在采集或传输过程中不可避免地受到噪声污染,造成图像质量的退化。这样的图像不仅影响视觉效果,而且还阻碍了图像视频编码、识别、场景理解等计算机视觉应用。因此,图像去噪一直是图像处理中一个重要的研究课题。高效合理地去除噪声,同时保留图像原本的特性是去噪算法的关键。
针对图像去噪,研究人员提出大量的算法。这些算法主要在空间域或频率域上利用滤波技术重建图像。以Gaussian滤波去噪为主的算法平滑效果好,但是边缘轮廓以及图像结构遭到破坏;另一方面,以各向异性滤波去噪为主的算法具有较好的保边效果,但易引入阶梯人造特征。文献[1]提出了一种异于传统去噪算法的新方法——非局部均值(non-local means,NLM)去噪算法,利用局部图像块(patch)冗余结构信息,将图像中结构相似的像素采用加权平均来获得去噪估计值。由于图像块比单个像素更好地表达图像结构信息,在不损失图像细节的情况下表现出优良的去噪性能,故其性能优于其他的经典去噪算法。NLM虽然性能优越,但效率与参数需要进一步优化。近年,很多学者对NLM提出了改进方法,这些方法主要集中在以下方面:1)降低计算复杂度(K-SVD[2-3]、DCT[4]、Walsh-Hadamard投影[5]、主成分分析[6-7])。2)优化参数[8-12](平滑核参数、相似邻域的尺寸和搜索区域的大小),提高性能。3)以NLM思想为基础,融合其他算法以提升去噪性能[13-14]。
本文针对NLM算法存在的问题,提出以下改进:1)针对算法计算复杂度高的问题,在搜索窗口内可能有很多不相似的块,利用
一般加性噪声图像的去噪模型可表示为:
| $ v(n,m)=u(n,m)+\gamma (n,m) $ |
式中,n, m代表二维图像空间像素的坐标值;v(n, m)代表坐标为(n, m)的受噪声污染的图像像素值;u(n, m)代表无噪声污染的真实图像值;γ(n, m)代表高斯加性白噪声。对于一张大小N×M的二维图像v(n, m),在NLM去噪算法中,对u(n, m)的估计值定义为:
| $ u[f][n,m]=\sum\limits_{k=0}^{N-1}{\sum\limits_{l=0}^{M-1}{w}}[n,m;k,l]f[k,l] $ | (1) |
其中
| $ \begin{array}{l} w[n,m;k,l] = \frac{1}{{Z[n,m]}}{{\rm{e}}^{ - \frac{{\left\| {N[{{\mathit P}_{n,m}}] - N[{{\mathit P}_{k,l}}]} \right\|_{2,a}^2}}{h}}}\\ \;\;\;\;\;\;Z[n,m] = \sum\limits_{k = 0}^{N - 1} {\sum\limits_{l = 0}^{M - 1} {{{\rm e}^{ - \frac{{\left\| {N[{{\mathit P}_{n,m}}] - N[{{\mathit P}_{k,l}}]} \right\|_{2,a}^2}}{h}}}} } \end{array} $ |
式中,
对图像每个像素点进行
由于经典的NLM算法的去噪效果好,大量文献都希望通过降低计算复杂度来改进算法,以此达到推广应用的目的,其中降低度量像素间的相似性计算量是主要的改进方向。文献[2]提出利用K-SVD(singular value decomposition)分解技术降低维数从而减少计算量。文献[4]在离散余弦变换的低频系数子空间内度量像素间的相似性。文献[5]利用Walsh-Hadamard变换的快速运算和能量集中特性,通过投影到低维子空间进行度量像素点之间的相似性,减少高维计算。文献[6-7]通过主成分分析方法将图像块投影到低维子空间,并在该低维子空间中度量像素点之间的相似性。文献[15]利用图像块的均值和方差聚类图像块避免权值低的图像块的欧氏距离计算。这些方法主要是通过变换在子空间里度量相似性,减少计算时间,但同时会影响去噪效果。
本文的思路与文献[15]具有一定的相似,利用选择性计算欧氏距离降低运行时间。通过逐次消元法判定剔除相似性低的图像块。文献[15]需要计算图像块的均值和方差并聚类,本文的方法仅需简单的加法运算,从而大幅度地降低了计算量。
2.1 基于逐次消元法的加速策略逐次消元法[16]本质上是一种利用范数不等式淘汰冗余点的快速全局搜索算法,减少平均绝对差(mean absolute difference,MAD)和计算量,有效地降低算法复杂性,同时可以提供与全搜索算法相同的结果。逐次消元法在视频目标运动估计等应用中取得良好的效果。
X表示以(n,m)为中心的图像块像素灰度值的向量,Y(k, l)表示搜素窗口内的以(k, l)为中心的图像块像素灰度值的向量。首先考虑L1范数相似度度量方式应用不等式
根据L1范数与L2范数的边界定义可知,
| $ {G_{\rm{ \mathsf{ σ} }} } \times \frac{{\left| {\sum\limits_{i = - b}^{i < b} {\sum\limits_{j = - b}^{j < b} {I(n + i,m + j)} } - \sum\limits_{i = - b}^{i < b} {\sum\limits_{j = - b}^{j < b} {I(k + i,l + j)} } } \right|}}{{2b + 1}} \leqslant\\ \ \ \ {G_{\rm{ \mathsf{ σ} }} } \times \sqrt {\sum\limits_{i = - b}^{i < b} {\sum\limits_{j = - b}^{j < b} {{{(I(n + i,m + j) - I(k + i,l + j))}^2}} } } $ | (2) |
式(2)中的高斯加权计算可以忽略。在搜索窗口S中可能有很多不相似的图像块,在去噪估计时,这些图像块对应的像素分配的权重越小越好。由于NLM算法使用指数形式的权重函数,当不相似的图像块较多时,这些小的权重值总和将较大,这对去噪过程将产生不利影响。因此,本文的NLM算法不再用搜索窗口S中所有的像素点,而是在搜索窗口S中选取q个权值
| $ \frac{{\left| {{{\left\| \mathit{\boldsymbol{X}} \right\|}_1} - {{\left\| {\mathit{\boldsymbol{Y}}(i,j)} \right\|}_1}} \right|}}{{2b + 1}} \leqslant {\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{Y}}(k,l)} \right\|_2} $ | (3) |
如果式(3)满足,需要计算
为了比较当前像素点是否满足式(3),需要计算
| $ II(x,y) = \sum\limits_{x' < x,y' < y} {I(x',y')} $ | (4) |
式中,
临时变量
| $ X(x,y) = X(x,y - 1) + I(x,y) $ | (5) |
| $ II(x,y) = II(x - 1,y) + X(x,y) $ | (6) |
| $ SII(x,y) = II(x + i,y + j) - II(x + i,y) - II(x,y + j) + II(x,y) $ | (7) |
通过式(5)、式(6)对原图像每个像素一次访问便可计算出图像积分图,用式(7)可以快速计算出图 1中窗口
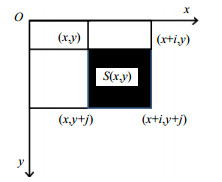 |
| 图1 计算窗口S(x, y)的积分示意图 |
积分图创建以后,只需要进行7次加法和1次除法运算,可以得出逐次消元法淘汰冗余点的条件。由于需要寻找前q个权值高的像素点,在极端情况下,如果每次检查点都满足式(3),那么采用逐次消元法并不能降低其计算量。为了减少该情况发生,在计算图像块间距离前,先对搜索窗口内所有图像块与以(n, m)点构成的图像块以均值为度量进行类聚,选出q个与(n, m)点均值最近的像素点,作为起始选择点。图像块的均值利用积分图可以在初始时一次性计算得到,因此,时间复杂度并不会增加太多。
2.2 动态搜索区域传统的NLM算法为了减少计算量,搜索范围由整个图像区域压缩到中心像素周围一定大小的区域
文献[18]提出以近似估计PatchGP为图像块之间相似性的NLM去噪,对边缘信息去噪效果好以及图像细节保留较完整,但对低频噪声去除不够理想,平滑区域易出现块状斑迹。由于PatchGP既可以反映图像相似结构,又能利用测地线距离找到同质信息。因此,本文根据PatchGP为线索搜寻同质信息来动态调整搜索窗口的方向与大小。
在图像I中的图像块c和d的PatchGP定义为:
| $ {D^{{\rm PatchGP}}}(\mathit{\boldsymbol{c}},\mathit{\boldsymbol{d}}) = \mathop {\min }\limits_\mathit{\Gamma } \sum\limits_{i = 1}^{{N_r} - 1} {\left\| {{N_I}(\mathit{\Gamma } ({p_{i + 1}})) - {N_I}(\mathit{\Gamma } ({p_i}))} \right\|} $ |
式中,
| $ {D^{{\rm PGP'}}}(\mathit{\boldsymbol{c}},\mathit{\boldsymbol{d}}) = \mathop {\min }\limits_\mathit{\Gamma } \sum\limits_{i = 1}^{{N_r} - 1} {\left\| {{N_I}(\mathit{\Gamma } ({p_i})) - {N_I}(\mathit{\boldsymbol{c}})} \right\|} $ | (8) |
| $ {C_{{\rm ratio}}} = \frac{{\sum\limits_{i = - r}^r {\sum\limits_{j = - r}^r {\mathit{\boldsymbol{I}}(i,j) \in {\rm NN}(q)} } }}{{(2r + 1) \times (2r + 1)}} $ | (9) |
式中,
图 2b所示为图 2a标准图像Barbara的手臂部分,图像块P与P1、P2、P3相比,P1、P3与P结构更相似。在搜索窗口S里,P3被漏掉,没有充分利用图像结构冗余的特点寻找到同质区域。采用以中心像素的S区域计算相似度,然后在S区域边缘像素和中心像素使用式(8)的
| $ \partial s_i^{\min } = \arg \min \left\{ {{D^{{\rm PGP'}}}(\mathit{\boldsymbol{c}},\partial {s_i}),{\rm{ }}{D^{{\rm PGP'}}}(\mathit{\boldsymbol{c}},\partial {s_i}) \ne \infty } \right\} $ | (10) |
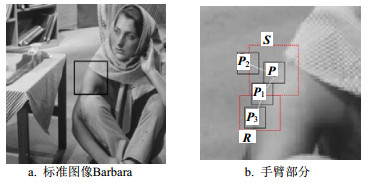 |
| 图2 PatchGP调整搜索范围 |
式中,
像素点I(n, m)的邻域搜索范围确定流程如下:
1) 初始化。以I(n, m)中心点的(2s+1)×(2s+1)搜索区域S;利用逐次消元法,计算区域S与中心像素点之间的相似度矩阵。
2) 用式(10)找到PatchGP最小的边缘点,以该边缘点为矩形边中心扩展大小为(2r+1)×(2r+1)的区域R,
3) 如果
4) 最终区域S为I(n, m)的邻域搜索范围,并得到与中心点的相似度。
3 实验结果与分析本文采用4个标准的图像Lena、Pepper、Barbara和Baboon,并加入多个取值的标准差σ的零均值高斯白噪声。在实验中,本文的方法分别与K-SVD- NLM[2]、DCT-NLM[4]、FM-PatchGP[18]、cNLM[19]和BM-3D[20]共5种基于块相似性的去噪算法从速度和性能两方面做定性比较与分析。其中,cNLM代表经典优化参数的NLM算法,DCT-NLM代表变换子空间去噪法、FM-PatchGP、K-SVD-NLM、BM-3D代表去噪性能最佳的方法。为了比较的公平,所有比较算法的搜索窗口和图像块大小参考文献[15]分别设置为21×21和7×7。本文的算法参数设置
为了验证本文的方法加速和自适应搜索范围的有效性,本文的算法和DCT-NLM均使用C++语言编程实现,cNLM和K-SVD-NLM源代码来自文献[19],FM-PatchGP和BM-3D源代码来自作者网站,测试环境为visual C++ 2008、Dell Inspiron、Core i3、2 GB内存。采用PSNR(peak signal-to-noise ratio)和SSIM(structural similarity index)两个指标对去噪结果进行定量比较。SSIM是一种以度量两幅图像间的结构性失真来评估图像质量评价度量的新指标,取值范围[0~1],其值越大越接近,当图像完全一致时,SSIM为1。
图 3和图 4所示分别为6种算法在
 |
| 图3 改进算法与K-SVD-NLM、DCT-NLM、FM-PatchGP、cNLM和BM-3D用PSNR指标的比较 |
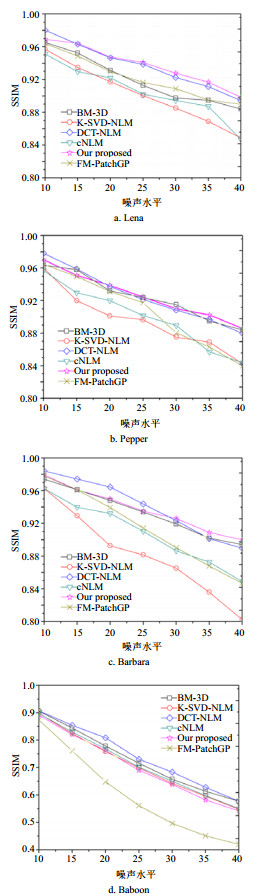 |
| 图4 改进算法与K-SVD-NLM、DCT-NLM、FM-PatchGP、cNLM和BM-3D用SSIM指标的比较 |
从PSNR、SSIM两个指标数值上可得,本文的算法都比cNLM算法有较大的提高。本文的算法虽然当
由于图 3d的测试图像Baboon存在细腻且不规则的纹理,本文的算法降低了自适应搜索区域能力,退化为较小固定搜索窗口的NLM且噪声干扰无法辨别,导致PSNR数值下降较快,性能略低于cNLM,但图 4d说明图像整体结构保留较好,同样由于不规则细腻的纹理导致PatchGP不够准确,FM-PatchGP的PSNR和SSIM值都下降较快。
图 5所示为Barbara图像部分细节原图以及6种算法去噪后的对比图(σ=25)。图 5a包含了左上角的平滑区域和头巾部分的纹理边缘区域。对比可见,除了FM-PatchGP,其他的5种算法都可以较好地保留图像的结构与细节。cNLM、K-SVD-NLM和BM-3D算法去噪结果的平滑区域部分不同程度出现明显的伪影。本文的算法将结构相似性和同质信息相结合动态调整搜索窗口,有效地去除了噪声干扰,较好地利用了图像冗余相似性,其边缘区更整齐,图像结构信息保留较完整。由于选取相似性最接近的q个像素点,对于平滑区域,该算法的去噪能力也明显强于cNLM,避免了伪影现象。与DCT-NLM算法相比,本文的算法对图像的边界细节纹理信息保留得稍好,图像细节更清晰。
 |
| 图5 6种算法去噪细节对比(σ=25) |
逐次消元法剔除相似性低的图像点和优化的搜索窗口都有效地降低了计算复杂度。表 1记录了本文的算法与K-SVD-NLM、DCT-NLM、FM-PatchGP、cNLM和BM-3D对本文测试的4幅图像的平均耗时比较。从表中可以看出,对于大小为128×128和256×256的图像,FM-PatchGP耗时最少,但其去噪性能较低以及图像细节丢失严重。对于大小为512×512和1 024×768的图像,由于本文的算法使用逐次消元法剔除像素点,图像越大,相似度低的像素点被丢弃得越多。该算法计算量增幅较小,与其他几种算法相比,具有良好的加速效果。
| 表1 本文的算法与比较算法不同图像大小的平均耗时比较 |
综上分析,从总体性能指标来看,本文的算法具有一定的优势。同时,该方法也存在如下两点不足:1)不太适应含有较多的细腻且不规则的纹理图像。2)从去噪指标和运行时间比较看,对于噪声σ<20和低于256×256大小的图像,该算法的整体性能略低于DCT-NLM算法。
4 结论NLM算法具有较好的去噪性能,但存在运行效率低的问题,本文利用L2范数的逐次消元法和积分图,有效地降低了像素间相似性计算强度,并根据图像空间相关性强的特点,提出一种基于Patch测地线距离寻找同质信息的自适应调整搜索窗口的方法。在实验中,本文的算法与当前性能最佳的5个基于图像块去噪算法相比,从PSNR、SSIM两个指标和运行时间比较上可知,该方法不但获得了较好的加速,而且去噪效果也有一定的提升。
| [1] |
BUADES A, COLL B, MOREL J M. A review of image denoising algorithms, with a new one[J].
Multiscale Modeling & Simulation, 2005, 4(2): 490–530.
|
| [2] |
ELAD M, AHARON M. Image denoising via sparse and redundant representations over learned dictionaries[J].
IEEE Transactions on Image Processing, 2006, 15(12): 3736–3745.
DOI:10.1109/TIP.2006.881969 |
| [3] |
ORCHARD J, EBRAHIMI M, WONG A. Efficient nonlocal-means denoising using the SVD[C]//Proceedings of IEEE International Conference on Image Processing. San Diego, California: IEEE Signal Processing Society, 2008: 1732-1735.
|
| [4] |
胡金蓉, 蒲亦非, 张意, 等. DCT子空间的非局部均值去噪算法[J].
计算机辅助设计与图形学学报, 2012, 24(1): 89–96.
HU Jin-rong, PU Yi-fei, ZHANG Yi, et al. Nonlocal-means denoising algorithm based on DCT subspace[J]. Journal of Computer-Aided Design & Computer Graphics, 2012, 24(1): 89–96. |
| [5] |
张志, 王润生. 基于Walsh-Hadamard投影的快速Nonlocal- means图像去噪[J].
宇航学报, 2011, 32(2): 380–387.
ZHANG Zhi, WANG Run-sheng. Fast nonlocal-means image denoising method based on Walsh-Hadamard Pro- jection[J]. Journal of Astronautics, 2011, 32(2): 380–387. |
| [6] |
TASDIZEN T. Principal components for nonlocal-means image denoising[C]//Proceedings of IEEE International Conference on Image Processing. San Diego, California: IEEE Signal Processing Society, 2008: 1728-1731.
|
| [7] |
ZHANG L, DONG W, ZHANG D, et al. Two-stage image denoising by principal component analysis with local pixel grouping[J].
Pattern Recognition, 2010(43): 1531–1549.
|
| [8] |
VAN DE VILLE D, KOCHER M. Nonlocal means with dimensionality reduction and SURE-based parameter selection[J].
IEEE Transactions on Image Processing, 2011, 20(9): 2683–2690.
DOI:10.1109/TIP.2011.2121083 |
| [9] |
VAN D E VILLE D, KOCHER M. SURE-based nonlocal-means[J].
Signal Processing Letters, 2009, 16(11): 973–976.
DOI:10.1109/LSP.2009.2027669 |
| [10] |
SALMON J. On two parameters for denoising with nonlocal-means[J].
Signal Processing Letters, 2010, 17(3): 269–272.
DOI:10.1109/LSP.2009.2038954 |
| [11] |
王志明, 张丽. 自适应的快速非局部图像去噪算法[J].
中国图象图形学报, 2009, 14(4): 669–675.
WANG Zhi-ming, ZHANG Li. Adaptive fast nonlocal image denoising algorithm[J]. Journal of Image and Graphics, 2009, 14(4): 669–675. DOI:10.11834/jig.20090416 |
| [12] |
LIU Y L, WANG J, CHEN X, et al. A robust and fast nonlocal-means algorithm for image denoising[J].
Journal of Computer Science and Technology, 2008, 23(2): 270–279.
DOI:10.1007/s11390-008-9129-8 |
| [13] |
FENG C S, MING L, WEI Z, et al. Edge preserving image denoising with a closed form solution[J].
Pattern Recognition, 2013, 46(3): 976–988.
DOI:10.1016/j.patcog.2012.08.014 |
| [14] |
CHEN Q, SUN Q, XIA D. Homogeneity similarity based image denoising[J].
Pattern Recognition, 2010, 43(12): 4089–4100.
DOI:10.1016/j.patcog.2010.07.002 |
| [15] |
MATHEW A T. Robust estimation approach for nonlocal-means denoising based on structurally similar patches[J].
International Journal of Open Problems in Computer Science and Mathematics, 2009, 2(2): 311–331.
|
| [16] |
WANG H S, MERSEREAU R M. Fast algorithms for the estimation of motion vectors[J].
IEEE Transactions on Image Processing, 1999, 8(3): 435–438.
DOI:10.1109/83.748899 |
| [17] |
VIOLA P, JONES M J. Robust real-time face detection[J].
International Journal of Computer Vision, 2004, 57(2): 137–154.
DOI:10.1023/B:VISI.0000013087.49260.fb |
| [18] |
CHEN X, KANG S B, YANG J, et al. Fast patch-based denoising using approximated patch geodesic paths[C]// IEEE Conference on Computer Vision and Pattern Recognition. Portland, OR: IEEE Signal Processing Society, 2013: 4321-4328.
|
| [19] |
DABOV K, FOI A, KATKOVNIK K O, et al. Image denoi- sing by sparse 3D transform domain collaborative filtering[J].
IEEE Transactions on Image Proscessing, 2007, 16(8): 2080–2095.
DOI:10.1109/TIP.2007.901238 |
| [20] |
WANG Z, BOVIK A C, SHEIKH E P. Image quality assessrment: Form error visibility to structural similarity[J].
IEEE Transactions on Image Proscessing, 2004, 13(4): 600–612.
DOI:10.1109/TIP.2003.819861 |
 2015, Vol. 44
2015, Vol. 44
