目标跟踪是计算机视觉领域的一个重要研究课题，其任务是模拟出运动物体在图像序列中的运动轨迹。粒子滤波算法^[1]使用一组带权粒子模拟目标状态的后验概率分布，在目标跟踪领域越来越受到人们的关注，尤其在解决非线性、非高斯的问题上。传统的粒子滤波算法采用若干维参数定义的简单几何图形表示跟踪结果，而现实中的物体往往具有复杂形状并伴有姿态、尺度变化等，难以被简单几何图形所描述。不精确的目标表示还会在目标更新阶段引入噪声像素，导致跟踪任务的失败。

许多算法尝试引入轮廓及分割技术实现动态跟踪任务。文献[2]基于形状演化以及相似性参数定义动态先验模型，并把其应用在粒子滤波框架中。在文献[3]提出的轮廓跟踪算法中，轮廓被参数化为椭圆，并使用隐马尔可夫模型估计当前轮廓状态。与以上参数化模型相比，水平集主动轮廓技术^[4-5]作为一种曲线的非参数表示法，能处理曲线的拓扑结构变化，应用广泛。在水平集模型中，轮廓线用高维函数的零水平集表示，并以高维函数的形式进行演化，直到最小化基于图像的能量函数。

水平集方法被用于跟踪技术^[6-7]。文献[8]提出一个概率框架，用于跟踪多个事先不可见的物体。利用观测图像数据计算目标位置、相对深度以及由水平集表示的目标形状的后验概率。文献[9]在贝叶斯框架中引入形状先验统计知识，以实现基于水平集的序列跟踪技术。文献[10]在粒子滤波框架中引入Mumford-Shah模型，在粒子滤波预测阶段，依据先前时刻的状态和观测数据，在各候选位置上执行水平集曲线演化。文献[11]在此基础上将算法改进为在更新阶段执行水平集演化，从而依据当前时刻的状态进行观测。然而这些算法使用的都是原始水平集演化模型，即仅依据图像信息而不考虑跟踪目标的因素，得到的跟踪结果依赖于初始曲线。文献[12]用区域增长的方法将目标与背景区域分割为片段，并在水平集框架中提出基于片段的跟踪方法。

1 粒子滤波器

粒子滤波算法^[1]是一种基于序列蒙特卡罗思想的估计过程，其实质是随机模拟序列的使用样本并在贝叶斯框架下完成在线学习。令$\mathit{\boldsymbol{x_k}} \in {{\bf{R}}^n}$表示状态向量，$\mathit{\boldsymbol{z_k}} \in {{\bf{R}}^m}$表示在$k$时刻可见的观测，并满足状态转移与观测方程：

${\mathit{\boldsymbol{x}}_{k + 1}} = {f_k}({\mathit{\boldsymbol{x}}_k}) + {\mathit{\boldsymbol{u}}_k}$

(1)

${\mathit{\boldsymbol{z}}_k} = {h_k}({\mathit{\boldsymbol{x}}_{\rm k}}) + {\mathit{\boldsymbol{v}}_k}$

(2)

式中，${\mathit{\boldsymbol{u}}_k}$表示已知概率分布${p_{u,k}}$的随机噪声；${\mathit{\boldsymbol{v}}_k}$表示已知概率分布${p_{v,k}}$的观测噪声。

已知初始状态分布${\pi _0}(\mathit{\boldsymbol{x}})$、状态转移核函数${K_k}({\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{x}}_{k + 1}}) = {p_{u,k}}({\mathit{\boldsymbol{x}}_{k + 1}} - {f_k}({\mathit{\boldsymbol{x}}_k}))$以及给定状态变量的观测似然${p_k}({\mathit{\boldsymbol{z}}_k}|{\mathit{\boldsymbol{x}}_k}) = {p_{v,k}}({\mathit{\boldsymbol{z}}_k} - {h_k}({\mathit{\boldsymbol{x}}_k}))$，每个离散时刻，在给定以往观测序列${\mathit{\boldsymbol{z}}_{1:k}} = \{ {\mathit{\boldsymbol{z}}_1},{\mathit{\boldsymbol{z}}_2}, \cdots ,{\mathit{\boldsymbol{z}}_k}\} $的情况下，产生一套粒子$\{ x_k^i\} _{i = 1}^N$用于估计未知状态${\mathit{\boldsymbol{x}}_k}$的后验分布$p({\mathit{\boldsymbol{x}}_k}|{\mathit{\boldsymbol{z}}_{0:k}})$。

2 粒子导向的主动轮廓跟踪算法 2.1 主动轮廓模型

传统的主动轮廓模型(Chan-Vese)意在寻找一个分段常值函数$u$来近似灰度图像$I$的强度分布：

$ u(x,y)=\left\{ \begin{align} &{{c}_{1}} \ \ \ \ \ \ {\text{若}}(x,y){\text{在分界线}}C{\text{内}} \\ &{{c}_{2}} \ \ \ \ \ \ {\text{若}}(x,y){\text{在分界线}}C{\text{外}} \\ \end{align} \right. $

(3)

式中，${c_1}$和${c_2}$表示依赖于分界线$C$的常数。用水平集函数$\mathit{\Phi } $的零水平集表示$C$，$C$内部、$\mathit{\Phi } $取正值，$C$外部、$\mathit{\Phi } $取负值。定义与水平集函数$\mathit{\Phi } $有关的能量泛函：

$\begin{gathered} {E_{{\rm{CV}}}}({c_1},{c_2},\mathit{\Phi } ) = \iint_\mathit{\Omega } {{{\left| {I(x,y) - {c_1}} \right|}^2}{\rm{H}}(\mathit{\Phi } (x,y)){\rm{d}}x{\rm{d}}y + } \\ \iint_\mathit{\Omega } {{{\left| {I(x,y) - {c_2}} \right|}^2}[1 - {\rm{H}}(\mathit{\Phi } (x,y))]{\rm{d}}x{\rm{d}}y} + \\ \iint_\mathit{\Omega } {{\rm{ \mathsf{ δ} } _0}(\mathit{\Phi } (x,y))|\nabla \mathit{\Phi } (x,y)|{\rm{d}}x{\rm{d}}y} \\ \end{gathered} $

(4)

式中，$\mathit{\Omega } $为图像域；H为Heaviside函数；${\rm{ \mathsf{ δ} } _0}$为Dirac函数。其中，$\iint_\mathit{\Omega } {{{\left| {I(x,y) - {c_1}} \right|}^2}{\rm{H}}(\mathit{\Phi } (x,y)){\rm{d}}x{\rm{d}}y}$和$\iint_\mathit{\Omega } {{{\left| {I(x,y) - {c_2}} \right|}^2}[1 - {\rm{H}}(\mathit{\Phi } (x,y))]{\rm{d}}x{\rm{d}}y}$为函数$u$与图像$I$的相似度；$\iint_\mathit{\Omega } {{\rm{ \mathsf{ δ} } _0}(\mathit{\Phi } (x,y))|\nabla \mathit{\Phi } (x,y)|{\rm{d}}x{\rm{d}}y}$为分界线$C$的长度，起到平滑分界线的作用。固定水平集函数$\mathit{\Phi } $，${c_1}$和${c_2}$分别极小化能量泛函${E_{{\rm{CV}}}}$，可得：

${c_1} = \frac{{\iint_\mathit{\Omega } {I(x,y){\rm{H}}(\mathit{\Phi } (x,y)){\rm{d}}x{\rm{d}}y}}}{{\iint_\mathit{\Omega } {{\rm{H}}(\mathit{\Phi } (x,y)){\rm{d}}x{\rm{d}}y}}}$

(5)

${c_2} = \frac{{\iint_\mathit{\Omega } {I(x,y)[1 - {\rm{H}}(\mathit{\Phi } (x,y))]{\rm{d}}x{\rm{d}}y}}}{{\iint_\mathit{\Omega } {[1 - {\rm{H}}(\mathit{\Phi } (x,y))]{\rm{d}}x{\rm{d}}y}}}$

(6)

从式(5)~(6)可知，${c_1}$和${c_2}$分别表示轮廓线$C$内部和外部的图像强度均值。最小化泛函${E_{{\rm{CV}}}}$时，函数$u$足够接近图像$I$，即具有平均图像强度的分段函数足够接近原始图像，因此函数$u$的定义使得水平集模型更倾向于分割出具有一致性强度的区域。然而现实的目标物体往往具有多种强度分布，传统水平集模型的演化原理则使其不能有效地收敛到多强度分布的目标区域^[10-11]。

2.2 粒子权重

基于粒子滤波的主动轮廓跟踪算法，将表示目标位置与区域的粒子视作状态$\mathit{\boldsymbol{X}}$，$k$时刻的图像${\mathit{\boldsymbol{I}}_k}$视作观测。预测阶段，算法在原有样本$\{ \mathit{\boldsymbol{X}}_{k - 1}^{(1)},\mathit{\boldsymbol{X}}_{k - 1}^{(2)},$ $ \cdots ,\mathit{\boldsymbol{X}}_{k - 1}^{(N)}\} $的基础上按照分布${K_{k - 1}}(\mathit{\boldsymbol{X}}_{k - 1}^{(i)},{\mathit{\boldsymbol{X}}_k})$采样得到新样本$\{ \mathit{\boldsymbol{X}}_k^{(1)},\mathit{\boldsymbol{X}}_k^{(2)}, \cdots ,\mathit{\boldsymbol{X}}_k^{(N)}\} $，其经验分布：

${p^N}({\mathit{\boldsymbol{X}}_k}|{\mathit{\boldsymbol{I}}_{0:k - 1}}) = \frac{1}{N}\sum\limits_{i = 1}^N {{{\rm{ \mathit{ δ}} } _{\mathit{\boldsymbol{X}}_k^{(i)}}}({\mathit{\boldsymbol{X}}_k})} $

(7)

式(7)即为给定$k - 1$时刻前所有观测情况下对状态${\mathit{\boldsymbol{X}}_k}$的条件概率分布估计。而后在更新阶段，每个粒子按照其与$k$时刻观测${\mathit{\boldsymbol{I}}_k}$的似然程度被赋权：

$w_k^{(i)} = \frac{{p({\mathit{\boldsymbol{I}}_k}|\mathit{\boldsymbol{X}}_k^{(i)})}}{{\sum\limits_{i = 1}^N {p({\mathit{\boldsymbol{I}}_k}|\mathit{\boldsymbol{X}}_k^{(i)})} }}$

(8)

在具体实现中，可使用任意粒子滤波器得到该带权粒子集合，而后在粒子空间中引入主动轮廓模型，并定义粒子导向的曲线演化方程，使其最终收敛到具有最多重要权重粒子的区域。

2.3 粒子空间下主动曲线演化

令$\mathit{\boldsymbol{C}}(s) = {[x(s) \ y(s)]^T}$，$s \in [0,1]$表示${{\bf{R}}^2}$空间中的一条闭合曲线。给定目标以往的轮廓线${C_{0:k - 1}}$，$k$时刻及以往所有观测${\mathit{\boldsymbol{I}}_{0:k}}$，以及当前时刻的带权粒子集合$\{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} _{i = 1}^N$，$k$时刻的轮廓线${C_k}$的概率模型可用贝叶斯公式建立：

$\begin{gathered} p({C_k}|\{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} _{i = 1}^N,{\mathit{\boldsymbol{I}}_{0:k}},{C_{0:k - 1}}) \propto \hfill \\ \underbrace {p(\{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} _{i = 1}^N|{C_k})}_{\rm particles}\underbrace {p({\mathit{\boldsymbol{I}}_k}|{C_k})}_{\rm edge}\underbrace {p({C_k}|{C_{0:k - 1}})}_{\rm prior} \hfill \\ \end{gathered} $

(9)

式中，$p(\{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} _{i = 1}^N|{C_k})$表示曲线${C_k}$对重要粒子的包罗程度；$p({\mathit{\boldsymbol{I}}_k}|{C_k})$表示曲线${C_k}$在目标边界上的概率；$p({C_k}|{C_{0:k - 1}})$表示轮廓线的先验概率，在此认为候选轮廓具有相同的先验概率。

令${\mathit{\Omega } ^ + }$和${\mathit{\Omega } ^ - }$分别表示曲线${C_k}$内部与外部的图像区域，${C_k}$将粒子集合划分为内外两个子集：

${O^ + } = \{ \{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} |\mathit{\boldsymbol{X}}_k^{(i)} \in {\Omega ^ + }\} $

(10)

${O^ - } = \{ \{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} |\mathit{\boldsymbol{X}}_k^{(i)} \in {\Omega ^ - }\} $

(11)

则式(8)中基于粒子集的概率模型可分解为：

$p(\{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} _{i = 1}^N|{C_k}) \propto p({O^ + }|{C_k})p({O^ - }|{C_k})$

(12)

其中：

$p({O^ + }|{C_k}) \propto \sum\limits_{\{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} \in {O^ + }} {w_k^{(i)}} $

(13)

$p({O^ - }|{C_k}) \propto 1 - \sum\limits_{\{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} \in {O^ - }} {w_k^{(i)}} $

(14)

式(13)和式(14)分别表示曲线内包罗重要样本及曲线外不泄露重要样本的程度。

为驱使轮廓线运动到目标边界，使用图像边缘指示函数：

$g(x,y) = \frac{1}{{1 + |\nabla {G_\sigma } * I(x,y){|^2}}}$

(15)

式中，${G_\sigma }$表示标准方差为$\sigma $的二维高斯滤波器。当坐标变量$(x,y)$位于图像边缘时，图像梯度的幅值$|\nabla {G_\sigma }*I(x,y)|$相对很大，$g(x,y)$的值趋近于0；相反，当$(x,y)$远离图像边缘时，$g(x,y)$的值趋近于1。则式(8)中目标边界概率模型可定义为：

$p({\mathit{\boldsymbol{I}}_k}|{C_k}) \propto \sum\limits_{{{[x \ y]}^{\rm{T}}} \in {C_k}} {g(x,y)} $

(16)

定义轮廓线的能量函数，使得最小化该能量函数等同于最大化概率：

$ \begin{align} & E(C)=\iint_{ {{O}^{+}}}{-w_{k}^{(i)}{\rm d}X}+\iint_{ {{O}^{-}}}{w_{k}^{(i)}{\rm d}X}+ \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \xi \int_{ C}{g(x,y)}{\rm d}x{\rm d}y+\mu \oint_{\mathit{C}}{\rm{d}\mathit{s}} \\ \end{align} $

(17)

使用水平集函数$\mathit{\Phi } $的零水平集表示曲线$C$，即$\mathit{\Phi } (x,y) = 0$当且仅当对某个$s \in [0,1]$有$\mathit{\boldsymbol{C}}(s) = {[x \ y]^{\rm{T}}}$。这里采用符号距离函数：

$ \mathit{\Phi }(x,y)=\left\{ \begin{align} & d((x,y),C)\begin{matrix} {} \\ \end{matrix}\ \ \ \ \ \ \ \ \ \ {\rm{if}}{{[x\ y]}^{\rm{T}}}\in {{\mathit{\Omega }}^{+}} \\ & 0\begin{matrix} {} \\ \end{matrix}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {\rm{if}}{{[x\ y]}^{\rm{T}}}\ {\rm{at}}\ C \\ & -d((x,y),C)\begin{matrix} {} \\ \end{matrix}\ \ \ \ \ {\rm{if}}{{[x\ y]}^{\rm{T}}}\in {{\mathit{\Omega }}^{-}} \\ \end{align} \right. $

(18)

则式(16)的关于水平集函数的形式为：

$\begin{gathered} E(\mathit{\Phi } ) = \iint_{{\rm{ }}O} { - w_k^{(i)}\operatorname{H} (\mathit{\Phi } (X)){\rm{d}}X} + \\ \iint_{{\rm{ }}O} {w_k^{(i)}[1 - \operatorname{H} (\mathit{\Phi } (X))]{\rm{d}}X} + \\ \iint_{{\rm{ }}\mathit{\Omega } } {{\rm{ \mathit{ δ} } _0}(\mathit{\Phi } (x,y))[\xi g(x,y) + \mu |\nabla \mathit{\Phi } (x,y)|]{\rm{d}}x{\rm{d}}y} \\ \end{gathered} $

(19)

依据$k$时刻的观测及粒子集合，对能量函数$E$执行梯度下降演化曲线：

${\hat C_k} = {\rm{evo}}({e_k},{\mathit{\boldsymbol{I}}_k},\{ \mathit{\boldsymbol{X}}_k^{(i)},w_k^{(i)}\} _{i = 1}^N) = e_k^{(M)}$

(20)

式中，${e_k}$表示演化过程中的轮廓线，在能量$E$减小最快的方向上经过$M$次迭代：

${e^{(\tau )}} = {e^{(\tau - 1)}} - {\eta ^{(\tau )}}{\nabla _e}E$

(21)

式中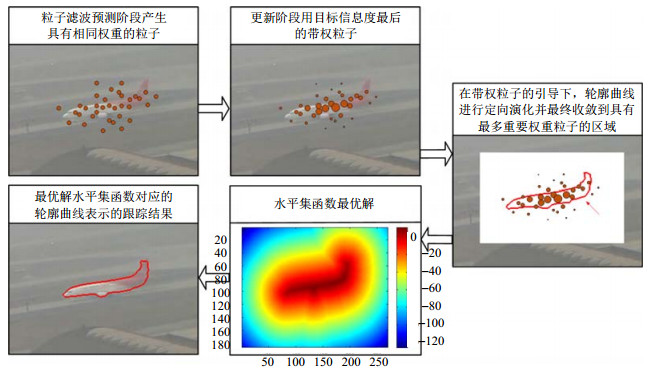，$\tau = 1,2, \cdots ,M$；${\rm{ }}{e^{(0)}} = {\hat C_{k - 1}}$。不同于基于原始的图像一致性原理的水平集模型，提出的方法在带权粒子的引领下进行定向演化，因而可以从较大范围的初始状态趋近目标，而不依赖初始曲线形态。以airport surveillance序列为例的跟踪流程图如图 1所示。

3 实验结果 3.1 目标检测与初始化

跟踪算法开始前需确定跟踪目标。通常可在第一帧中手动画出一个多边形来给出初始目标区域。本文采用针对运动飞机目标的自动检测与初始化方案。

采用背景建模方法与Haar特征对跟踪目标进行检测结果如图 2所示。首先采用基于空间局部二值模式的背景建模方法^[13]得到视频中的运动物体区域，即二值的背景减图像$B$。再根据飞机目标在运动方向上的对称性，在去噪后的运动物体区域上构建其各个角度的外接矩形，而后在这些外接矩形上使用Haar特征进行检测。

3.2 目标跟踪

得到目标初始区域后，在新的视频帧中可采用以往提出的任意一种粒子滤波算法来得到模拟目标分布的带权粒子集，从而应用提出的主动轮廓跟踪方法进行跟踪任务。在此采用基于表观和运动信息的粒子滤波器。首先对得到的初始目标区域进行表观建模，得到其RGB三通道的密度分布$q = {\{ {q^{(u)}}\} _{u = 1,2, \cdots ,m}}$，m=16为量化级数。而后，在后续的视频帧中采用前一时刻的跟踪结果作为初始目标区域，并在旧的粒子集上使用恒定位移模型产生一套新的粒子集。对每个粒子区域${p_i}$，统计其强度分布${p_i} = {\{ p_i^{(u)}\} _{u = 1,2, \cdots ,m}}$，并计算其与目标分布的相似性度量：

$ \rho [{p_i},q] = \sum\limits_{u = 1}^m {\sqrt {p_i^{(u)}{q^{(u)}}} } $

(22)

此外，在背景减图像$B$中统计该粒子区域的运动信息，得到该区域中前景像素个数${\rm fore}_i$。

最后，同时使用表观信息与运动信息为该粒子赋权值。粒子${p_i}$的权重为：

$ w(i) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\exp \left[ { - \frac{{d_i^2}}{{2{\sigma ^2}}}} \right] $

(23)

其中，

$ {d_i} = \alpha \rho [{p_i},q] + \beta {\rm fore}{_i} $

(24)

式中，$\alpha $与分别$\beta $表示表观信息与运动信息所占的比重，这里均设为0.5。

基于以上带权粒子，采用前面介绍的基于粒子滤波的主动轮廓跟踪算法对目标进行跟踪。此外，还将其与采用相同权值计算方法的标准粒子滤波器及以往的基于粒子滤波与主动轮廓的轮廓跟踪算法^[10]进行比较。比较算法在airport sunveillance序列上的跟踪结果如图 3所示。图 3描述了一个飞机在跑道上滑行的过程。为给出令人信服的比较结果，在相同的实验条件下执行3个算法。算法均采用前面所述的目标初始化方法，且都采用30个粒子样本。3个算法在序列上帧序号分别为284, 462, 663。可看出，标准的粒子滤波算法很难准确包罗整个目标区域，这是由于矩形框所表示的目标区域中含有大量的背景像素，由此建立的目标模型不能提供准确的信息以很好地区分目标和局部背景。这会导致算法的判断力弱化并使结果偏离目标的真实位置。当背景像素的污染逐步传递到后续图像帧造成误差累计时，跟踪器就会发生漂移现象。而轮廓跟踪方法^[10]在粒子滤波预测阶段产生的候选粒子上执行传统水平集模型而不考虑任何目标信息，使得其轮廓演化不关联目标物体而只趋近强度一致区域，因而在具有多特征分布的目标序列上，其曲线收敛结果受制于初始轮廓及图像特征，很难准确包罗整个目标区域。相比之下，提出的算法使用带权粒子引导主动轮廓线收敛到目标边界，可以精确地捕获目标区域。

3.3 静态飞机目标分割

除了上述对运动目标的跟踪应用外，在提出的基于粒子滤波的主动轮廓算法中，采用不同的粒子权值计算方法，可得到试用于不同应用的结果。例如，对于机场监控场景下的静态飞机，由于摄像机的摄像距离较远，照射角度大，所以大部分物体在场景中相对飞机都因为较小而变得不显著。由此，可采用显著度测量的方法来为粒子赋权值从而达到针对飞机目标进行主动轮廓分割的目的。在此采用文献[14]中的显著度计算方法，并结合显著区域下的haar特征值来为粒子赋权，即式(24)转变为：

$ {d_i} = \alpha 'S({p_i}) + \beta 'H({p_i}) $

(25)

式中，$S$为显著图；$H$为Haar特征值；$\alpha ' = 0.6$；$\beta ' = 0.4$。

最后基于此带权粒子执行提出的方法对飞机目标进行轮廓提取。在此也给出基于传统主动轮廓模型的分割方法^[4]的分割结果作为比较实验。提出的方法在机场监控视频中静态飞机目标提取上的应用如图 4所示。实验结果表明了提出算法在真实应用中的有效性。

4 结论

本文提出一种新的基于粒子滤波的主动轮廓跟踪算法，以实现对复杂形状物体的轮廓跟踪。相比于基于原始的仅依赖图像特征的主动轮廓模型，本文的方法充分考虑跟踪任务的上下文环境，使用目标状态后验分布的模拟样本定义轮廓能量函数，并引导曲线向具有重要权重粒子的区域进行定向演化，最终收敛到具有最大目标似然的图像区域，实现了对目标物体的全局运动及局部形态演化的同时估计。在机场监控视频序列上的各种应用结果证明了本文方法在实际应用中的有效性和鲁棒性。