电子科技大学学报  2015, Vol. 44 Issue (1): 97-100
引用本文
李浪, 邹祎, 贺位位, 李仁发. EPCBC密码算法的FPGA优化实现研究[J]. 电子科技大学学报, 2015, 44(1): 97-100.
LI Lang, ZOU Yi, HE Wei-wei, LI Ren-fa. Research on FPGA optimal implementation of EPCBC Cipher[J]. Journal of University of Electronic Science and Technology of China, 2015, 44(1): 97-100.
EPCBC密码算法的FPGA优化实现研究    [PDF全文]
李浪1,2 , 邹祎1 , 贺位位3 , 李仁发2     
1. 衡阳师范学院计算机系 湖南 衡阳 421002;
2. 湖南大学信息科学与工程学院 长沙 410082;
3. 电子科技大学计算机科学与工程学院 成都 611731
收稿日期: 2013-09-25; 修回日期: 2014-11-02
基金项目: 国家自然科学基金(61173036);湖南省自然科学基金(2015JJ4011);湖南省博士后基金(897203005)
作者简介: 李浪(1972-), 男, 博士, 教授, 主要从事嵌入式系统与信息安全方面的研究
摘要: 针对资源约束的智能卡加密需要小面积实现的问题, 对EPCBC加密算法从硬件上实现面积优化进行了如下研究:1)相同运算只实现一次, 主程序调用32次完成加密; 2)对S盒变换和密钥变换使用同一寄存器, 从而节省寄存器数量; 3)把密文轮操作和密钥更新放在一个模块中。通过FPGA优化结果表明, EPCBC密码算法实现面积大幅度减小, 优化率达到56%, 同时加密运算性能也没有降低, 从而为开发受资源约束的智能卡密码硬件提供可行方案。
关键词: 面积优化     EPCBC加密算法     FPGA     Verilog HDL    
Research on FPGA optimal implementation of EPCBC Cipher
LI Lang1,2, ZOU Yi1, HE Wei-wei3, LI Ren-fa2    
1. Department of Computer Science, Hengyang Normal University Hengyang Hunan 421002;
2. College of Information Science and Engineering, Hunan University Changsha 410082;
3. School of Computer Science & Engineering, University of Electronic Science and Technology Chengdu 611731
Abstract: In order to achieve small area implementation of encryption in resource-constrained smart cards, we studied the hardware optimal implementation of electronic product code block cipher(EPCBC) encryption algorithm. Firstly, each operation is accomplished only once, and the main program calls the 32 times to complete the encryption. Secondly, the same register is used in the S-box and key transformation so that the number of required registers is reduced. Thirdly, the cipher round operation and key update are put in the same module. Through field programmable gate array(FPGA) the experimental results show that the implementation area of EPCBC is greatly reduced, the optimization efficiency rate reaches 56%, and the encryption performance is not decreased so as to provide practical solutions for resource-constrained cryptographic smart cards.
Key words: area optimization     EPCBC cipher     FPGA     Verilog HDL    

随着物联网的应用深入，如何在射频识别(radio frequency identification, RFID)等智能卡上实现有效加密算法成为研究热点。物联网上的密码算法实现要求尽可能小的面积实现，它面向资源约束，同时又要保证加密效率。轻量级密码算法正是在这种应用背景下发展起来的，从文献[1]提出的PRESENT轻量级密码算法开始，文献[2]提出了PUFFIN算法、文献[3]提出了MIBS算法、文献[4-5]提出了PICCOLO和LED密码算法，其中LED被称为超轻量级密码算法，文献[6]提出了轻量级密码算法EPCBC。

EPCBC密码算法采用类PRESENT的构造方法，两个算法加密结构上相同，主要区别在于EPCBC对密钥更新部分进行了改变。密钥长度为96位，特别适用于物联网RFID的加密实现, 其加密效率优于AES和PRESENT密码算法。

AES等主流加密算法已有大量研究成果[7]，但目前国内外对EPCBC相关研究还非常少，因此对EPCBC密码算法的硬件优化研究具有一定的价值，可更好地促进EPCBC在面向资源约束的智能卡上加密实际应用[8-11]。

1 EPCBC密码算法原理

EPCBC密码算法有(48, 96)和(96, 96)两种实现形式。(48, 96)对应分组长度为48位，密钥长度为96位；(96, 96)对应分组长度为96位，密钥长度为96位，两种实现的加密运算都是32轮次。EPCBC密码的内部结构与PRESENT相似，只是分组长度、密钥更新、置换函数和查找表次数有区别。

EPCBC主要包括轮密钥加(AddKey)、S盒变换(SubCell)、P置换(Exchange)操作；同时对密钥key进行S盒变换(SubCell)、p置换(Exchange)操作、与轮数异或。本文以EPCBC(96, 96)为对象进行优化研究。

2 优化方法

密码算法硬件实现有速度优先和面积优先两种优化方法。

2.1 速度优先

速度优先方法一般采用全流水进行密码算法实现。EPCBC密码32轮运算中每轮运算的操作相同，若不考虑芯片面积的占用，可将32个轮运算模块均以硬件实现。在这种优化方法下，每一个数据块完成一次EPCBC轮运算后，立即开始下一级流水线计算。不考虑其他因素，此流水线方式在每个时钟周期有32个数据块同时串行处理，使得整个加密运算没有额外的等待时间。速度优先方法使数据处理速度比非流水线提高32倍，但它需要大量的硬件资源，即芯片实现面积增大。

2.2 面积优先

与速度优先方法相比，面积优先算法则是在硬件上相同功能模块只实现一次，然后重复调用。具体到EPCBC密码算法时，即在硬件上密钥加、S盒变换和P置换只实现一次，然后通过主程序重复调用32次完成32轮运算。该方法可极大地降低硬件开销。

EPCBC作为轻量级加密算法，面向资源约束的智能卡加密应用。本文主要考虑面积优先实现EPCBC密码，具体的优化方法如下：

1) 在硬件上相同运算只实现一次，主程序调用32次完成加密；

2) 同一个模块对明文S盒变换和密钥变换使用同一寄存器，从而节省寄存器数量；

3) 模块中所有语句并行执行，把对密文轮操作和密钥更新放在同一模块中，不会影响加密速度，不用保存密钥更新中间结果。在不影响加密速度的基础上，有效地节省寄存器数量；

4) 通过计数器cnt控制模块EPCBCRound调用的次数，实现加密过程；

5) 整个EPCBC密码算法都采用assign赋值实现，时钟信号控制计算器更新，完成加密只需32个时钟周期。

3 EPCBC优化部分实现与验证 3.1 EPCBCround核心部分优化

核心部分优化主要实现了上述优化方法中的1)、2)、3)、5)点。一轮EPCBC运算的优化方法用Verilog HDL语言描述如下：

module EPCBCRound(res, Up_k, state, key, r);

   input [4:0]   r;

   input [95:0]   key, state;

   output[95:0]   Up_k, res;

   wire  [95:0]   Up_k, res;

   reg   [3:0]  sbox[0:15];

   initial begin

   sbox[0]=12;sbox[1]=5;sbox[2]= 6; sbox[3]=11;

   sbox[4]=9;sbox[5]=0;sbox[6]=10; sbox[7]=13;

   sbox[8]=3;sbox[9]=14; sbox[10]=15;sbox[ 11]= 8;

   sbox[12]=4;sbox[13]=7;sbox[14]= 1;sbox[15]= 2;

   end

   wire  [95:0]  temp, s_k, s_res;

   assign    temp = state ^key; //AddKey

   SubCell(key)

   SubCell(state)

   Exchange(state)

   Exchange(key)

endmodule

仿真软件采用modelsim 6.1f，EPCBCRound仿真结果数据如表 1所示。

表1 EPCBCRound仿真结果

表中，test/r为算法轮数测试信号；数值00为第一轮测试运算；test/state为明文测试信号；test/key为密钥测试信号；test/res为输出结果信号(密文)；test/Up_k为密钥更新信号。

3.2 EPCBC主程序优化

EPCBC模块中，采用资源优先方式，实现上述优化方法的第4)。核心优化用Verilog HDL语言描述如下：

module EPCBC(res, state, key, clk);

   input   clk;

   input   [95:0] state, key;

   output [95:0] res;

   reg   ready=1;

   reg   switch=1;

   reg   [7:0]   cnt=8'hff;

   reg   [95:0]   res, k;

   wire   [95:0]  t_res, t_k;

     always @(posedge clk) begin

     cnt  ＜= (cnt^31)? cnt+1: cnt;

     ready  ＜= (cnt^31)? 1:0;

     switch＜=   ready? 1:0;

     res＜=ready?

(cnt^8'hff)?t_res:state) :((switch)?res^k:res);

    k＜= ready? ((cnt^8'hff)?t_k  : key) : k;

   end

   EPCBCRound  ER(t_res, t_k, res, k, cnt[4:0]);

Endmodule

EPCBC算法采用assign赋值实现，时钟信号控制计算器更新，完成加密只需32个时钟周期。使用EPCBC密码的原始测试数据进行仿真实验验证。

输入明文：0123456789ABCDEF01234567

密钥：0123456789ABCDEF01234567

EPCBC仿真实验结果如表 2所示。

表2 EPCBC仿真实验结果

表中，test/clk为时钟测试信号；test/state为明文测试信号；test/key为密钥测试信号；test/res为输出结果信号(密文)。从实验结果看可出优化后加密运算结果是正确的。

4 性能分析

对优化前后的EPCBC(96, 96)进行了FPGA实现，通过ISE 13.2对EPCBC综合下载进行性能分析，FPGA型号为xilinx virtex-5 LX50T。优化前的EPCBC密码算法FPGA实现面积如表 3所示，优化后的EPCBC密码算法FPGA实现面积如表 4所示。

表3 优化前的EPCBC密码算法FPGA实现面积
表4 优化后的EPCBC密码算法FPGA实现面积

表 3和表 4反映了EPCBC在实现FPGA时各部分的面积占用数。其中，Slice为EPCBC在FPGA上实现时的基本面积单元；LUT为EPCBC在FPGA上的表面积占用单元，第一行与第二行数值相加即为EPCBC的FPGA实现面积。

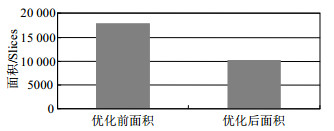
根据表 3可计算EPCBC密码算法优化前面积为17 801 Slices，根据表 4可计算优化后面积为10 036 Slices，优化效率达到56%。EPCBC面积优化效果如图 1所示。可看出优化后的EPCBC在面积资源占用上相比优化前有较大优势，特别适合资源约束的RFID加密应用实现。

图1 EPCBC面积优化效果图

优化后的EPCBC密码算法工作频率如下所示：

time summary:

Timing errors:0 score:0(Setup/Max:0, Hold:0)

Constraints cover 416717 paths, 16 nets, and 29917 connections

Design statistics:

  Minimum period:   9.971ns(Maximum frequency:100.291MHz)

  Maximum path delay from/to any node:   4.340ns

  Maximum net delay:   0.835ns

Analysis completed Fri Aug 23 10:53:03 2013

可看出系统时钟周期为9.971 ns。由此可得出优化后的EPCBC密码算法吞吐率为：

$ b /t=96/9.971=9.627 \ {\rm Gb/s} $ (1)

式中，b表示EPCBC密码算法的分组长度，单位为bit；t表示时钟周期。

可见，面积优化后的EPCBC密码算法加密效率仍然较高，即在面积优化的同时保证了EPCBC的加密速度。

5 结论

本文对EPCBC轻量级密码算法进行了面向面积优化的FPGA实现，优化方法不但有效降低了EPCBC密码的实现面积，同时实验结果表明其性能仍然得到了保证。后续工作将会对其安全性和效率展开进一步分析。

参考文献
[1]
BOGDANOV A, KNUDSEN LR, LEANDER G, et al. Present: an ultra-lightweight block cipher[C]//Proceedings of Cryptographic Hardware and Embedded Systems 2007. Vienna, Austria: Springer, 2007.
[2]
CHENG H, HEYS H, WANG C. Puffin: a novel compact block cipher targeted to embedded digital systems[C] //Proceedings of the 11th EUROMICRO Conference on Digital System Design Architectures Methods and Tools. Parma, Italy: IEEE, 2008.
[3]
IZADI M, SADEGHIYAN B, SADEGHIAN S, et al. MIBS: a new lightweight block cipher[C]//Proceedings of the Cryptology and Network Security 2009. Ishikawa, Japan: Springer, 2009.
[4]
SHIBUTANI K, ISOBE T, HIWATARI H, et al. Piccolo: an ultra-lightweight block cipher[C]//Proceedings of the Cryptographic Hardware and Embedded Systems 2011. Nara, Japan: Springer, 2011.
[5]
GUO J, PEYRIN T, POSCHMANN A, et al. The LED block cipher[C]//Proceedings of the Cryptographic Hardware and Embedded Systems 2011. Nara, Japan: Springer, 2011.
[6]
YAP H, KHOO K, POSCHMANN A, et al. EPCBC-a block cipher suitable for electronic product code encryption[C]// Proceedings of the Cryptology and Network Security 2011. Sanya, China: Springer, 2011.
[7]
GOOD T, BENAISSA M. AES on FPGA from the fastest to the smallest[C]//Proceedings of Cryptographic Hardware and Embedded Systems 2005. Edinburgh, UK: Springer, 2005.
[8]
XINMIAO Z, PARHI K. High-speed VLSI architectures for the AES algorithm[J]. IEEE Transactions on Very Large Scale Integration(VLSI) Systems, 2007, 12(9): 957–967.
[9]
LI C Y, CHIEN C F, HONG J H. An efficient area-delay product design for mixcolumns/invmixcolumns in AES[C]// Proceedings of the 2008 IEEE Computer Society Annual Symposium on VLSI. Montpellier, France: IEEE, 2008.
[10]
KUNDI DS, AZIZ A, IKRAM N. Resource efficient implementation of T-Boxes in AES on virtex-5 FPGA[J]. Information Processing Letters, 2010, 110(10): 373–377. DOI:10.1016/j.ipl.2010.03.004
[11]
LI Zhen-rong, ZHUANG Yi-qi, ZHANG Chao, et al. Low-power and area-optimized VLSI implementation of AES coprocessor for Zigbee system[J]. The Journal of China Universities of Posts and Telecommunications, 2009, 16(3): 89–94. DOI:10.1016/S1005-8885(08)60232-0