在移动自组网(mobile Ad hoc networks, MANETs)领域, 节点高速移动、节点稀疏、交替活跃及恶意攻击等因素造成网络在很多情况下不连通, 具有间歇连通的特点。这会导致节点对之间由于不存在通信路径而无法及时传输信息。所以, 以上应用必须能够容忍一定程度的延迟, 这类网络统称为延迟容忍网(delay tolerant network, DTN)[1]。由于传统MANETs路由策略的研究一般假设底层网络是连通的, 即任意收发节点对在传输数据之前存在一条完整的通信路径, 这些算法无法直接应用于DTN。
为了在不连通网络中进行数据传输, 节点需要把消息存储起来, 并跟着自身的移动随身携带, 直到遇到目的节点完成传输, 在此过程中节点可能需要把消息转发或复制到其他非目的节点上以提高路由效率, 事实上, 这也是DTN路由策略的核心, 这种方式称为存储-携带-转发工作模式。目前, DTN路由策略主要分为副本受限算法及副本非受限算法两类。副本受限算法是指算法最多产生L个副本, 当副本数达到L时, 只能向目的节点发送信息。这类算法中最简单的是直接传输(direct transmission, DT)[2], 在该策略中, 信息源只向目的节点发送消息, 中间不经过任何转发, 即L=1, 因此其延迟非常大, 传输成功率也很低。为了提高效率, 人们考虑提高L的值, 采用多副本策略, 这类算法的核心是L个副本如何传播, 最早有喷射等待(spray and wait, SW)[3]算法, SW采用二分法, 此后出现了一系列改进[4-5]。这些算法的本质是尽量利用传播能力强的节点来提高传播效率。副本非受限算法是指没有明确限定能够产生多少副本的算法, 最基础的是泛洪(flooding)。在泛洪策略中, 携带消息的节点每次遇到没有携带消息的节点都把消息进行转发(不管是不是目的节点), 显然这种策略冗余非常大且需要耗费大量的节点能量。为了提高效率, 文献[6-8]提出了把消息尽可能转发到最有可能完成消息传输的节点上, 从而在保证效率的前提下降低消息副本量。这些算法虽然效率较高, 但计算量较大且需要额外的空间来存储计算所需的信息, 为此, 人们提出了一些计算量较小且性能不错的算法, 如two-hop算法。该算法允许信息源向任何节点发送消息, 而其他携带消息的节点只能向目的节点发送消息。two-hop算法虽然通过限制转发节点降低了资源消耗, 但信息源仍可能产生大量副本, 在能量受限的情况下会带来问题。因此, 在有限的资源消耗约束下如何提高信息分发的效率是two-hop算法研究的重点, 这也是本文要解决的主要问题。值得说明的是, 对于副本受限算法, 当达到最大副本量时, 消息也可能会进一步在网络中传输, 只是此时转发消息的节点需要删除自己所存储的副本。从这个意义上讲, 之前讲到的发送或转发都等同于复制, 本文也采用同样的概念。
目前针对two-hop算法的优化控制问题已经有了一定的研究。文献[9]采用离散时间Markov模型研究了two-hop算法最优控制问题。文献[10]采用连续时间Markov过程进一步深入研究、探讨了动态概率传输策略。文献[11-12]分别探讨了异构节点及存在恶意节点情况下的最优控制问题。以上研究都假设网络模型服从负指数分布, 虽然这一假设在一些人工数据集如Random Waypoint中成立, 但它无法描述节点之间边动态变化的依赖关系。文献[13]指出这一点在真实网络中普遍存在并且提出了Edge-Markov模型, 探讨了Edge-Markov模型中Flooding算法的执行时间问题。文献[14]针对文献[13]模型探讨了消息大小对泛洪算法的影响。但目前还没有基于Edge-Markov模型对路由算法进行最优控制的研究。本文主要贡献概括如下:1)基于Edge-Markov模型, 采用离散时间Markov过程来建模two-hop算法;2) 针对上述模型, 从理论上证明最优概率服从阈值形式, 任何非阈值形式的发送策略都不可能是最优策略; 3)仿真及数值结果证明了理论的正确性。
1 网络模型假设网络中有N+1个节点, 最后一个节点称为目的节点D, 前N个节点可以产生消息。简单起见, 假设其中的一个节点(称为信息源S)产生消息m, 其他N-1个节点称为中转节点。采用离散时间模型, 每个时间间隔(称为时隙)为θ, 第t个时隙是指时间区间[tθ, (t+1)θ]。信息源在第一个时隙开始产生消息m, m的最大生存周期为T(T个时隙)。对于任意两个节点i和j, 它们之间的边为eij。eij=1表示节点i和j处于连接状态, 可以相互通信; eij=0意味着二者处于断开状态。网络中任何一条边的状态转换关系如图 1所示[15]。
 |
| 图1 边的状态转换图 |
上述转换是一个2状态的马尔科夫过程, 存在稳定分布, 因此有:
| $ \left\{ \begin{array}{l} {\pi _0}\alpha = {\pi _1}\beta \\ {\pi _0} + {\pi _1} = 1 \end{array} \right. $ | (1) |
式中, π0和π1分别是在稳定状态边处于断开及连通状态的概率。从式(1)可以得到:
| $ \left\{ \begin{array}{l} {\pi _0} = \beta /(\alpha + \beta )\\ {\pi _1} = \alpha /(\alpha + \beta ) \end{array} \right. $ | (2) |
本文采用概率two-hop算法, 即信息源在每次遇到中转节点时不是绝对发送, 而是以一定概率进行发送, 以p(t)表示在第t个时隙所采取的概率。该概率可称为发送概率或发送策略, 它是一个随机序列[9], 在任意时刻都可以看做一个随机变量, 如在第t个时隙, p(t)就是随机变量, 可以在[0, 1]中任意取值。下面首先给出阈值概率的定义。
定义 1 如果存在一个正常数h, 在t < h时, p(t)=1;在t=h时, p(t)=p(0≤p < 1);在t > h时, p(t)=0, 则称为阈值概率。
需要注意的是, 这里的发送概率主要是指信息源与中转节点之间的发送概率。而任何携带消息的节点(包含S)都以概率1向目的节点D发送消息。
2 系统建模假设在第t个时隙末携带消息的节点数为X(t), E(X(t))表示对应的期望值。进一步假设每一个接受消息的节点只能在下一时隙才能进行转发, 且消息足够小从而能够在一个时隙内完成传输, 显然X(0)=1。因为路由策略的能量消耗与转发次数成正比, 为简单起见, 直接利用转发次数作为能量消耗的指标[9-12]。采用类似的方法, 即用X(t)表示从时刻0到第t个时隙总共消耗的能量值。令F(t)表示在第t个时隙传输成功的概率(目的节点D得到消息)。如果限定为传输一条消息, 允许消耗的最大能量为δ, 则存在问题:
| $ \left\{ \begin{array}{l} {\rm{Maximize }} \;\;F(T)\\ {\text{Subject to }}\;\;E(X(T)) \le \delta \end{array} \right. $ | (3) |
上述优化问题是指在有限的能量约束条件下最大化传输成功率。X(t)的演化规律为:
| $ X(t + 1) = X(t) + \sum\limits_{j \in \Omega (t)} {{\phi _{t, t + 1}}(j)} $ | (4) |
式中, Ω(t)是在第t个时隙没有携带消息的节点集合, 且满足|Ω(t)|=N-X(t);
| $ {\phi _{t, t + 1}}(j) = \alpha p(t + 1) = \left\{ \begin{array}{l} \alpha \;\;\;\;t < h\\ 0 \;\;\;\;t > h \end{array} \right. $ | (6) |
当t > h时, 其发送概率为0, 因此j得到消息的概率为0;在t < h时, 由于发送概率为1, 节点j在第t个时隙没有得到消息, 说明此时边eSi处于断开状态。因此, 如果在第t+1个时隙节点j要得到消息, eSi必须从0变为1, 这一概率为α, 所以式(6)成立。当t=h时, 由于上一时隙发送概率为1, 可知值为αp。
根据式(4)可以得到X(t)的期望值为:
| $ E(X(t + 1)) = E(X(t)) + (N-E(X(t))){\phi _{t, t + 1}}(j) $ | (7) |
进一步可以得到:
| $ E(X(t)) = N-(N-1)\prod\limits_{i = 0}^{t-1} {(1 - {\phi _{i, i + 1}}(j))} $ | (8) |
对于目的节点D, 如果它在第t(t > 1)个时隙(当t=1时, 只有S能满足D, 此概率为π1)得到消息, 且在此之前没有得到, 则此概率为:
| $ \begin{array}{c} F(t-1, t) = \\ 1-\prod\limits_{i \in \chi (t-2)} {{p_{iD}}(t - 1, t)} \prod\limits_{j \in \chi (t - 1)\backslash \chi (t - 2)} {{p_{iD}}(t - 1, t)} = \\ 1 - {(1 - \alpha )^{X(t - 2)}}{\pi _0}^{X(t - 1) - X(t - 2)} \end{array} $ | (9) |
式中, χ(t)代表在第t个时隙得到消息的节点集合, 且满足|χ(t)|=X(t); piD(t-1, t)代表目的节点D在第t个时隙从节点i得到消息。对于χ(t-2)中的节点, 它们在第t-2个时隙已经得到消息, 所以如果D在第t-1个时隙与它们相遇, 则D即可得到信息, 因此如果D没有得到信息, 就可以知道D与χ(t-2)中的节点在第t-1个时隙处于断开状态。进一步, 如果D在第t个时隙仍没有得到信息, 则D与它们中的任何一个节点之间的边仍然处于断开状态(即在状态0保持不变), 满足piD(t-1, t)=1-α。在第t-1个时隙得到消息的节点集合可以表示为χ(t-1)\χ(t-2), 由于这些节点刚刚得到信息, 则无法在本时隙内进一步把信息转发到其他节点, 所以即使这些节点在第t-1个时隙与D处于连接状态, D仍无法从它们得到信息, 因此它们之间的边在第t-1个时隙可以处于任何状态, 所以在t时刻D没有得到信息的概率为π0。
为了计算F(t), 本文借鉴文献[9]中的方法, 令H(t)=1-F(t), 则有:
| $ \begin{array}{c} H(t + 1) = H(t)E(1-F(t, t + 1)) = \\ H(t){(1-\alpha )^{E(X(t-1))}}{\pi _0}^{E(X(t) - X(t - 1))} \end{array} $ | (10) |
进一步可以得到:
| $ \left\{ \begin{array}{l} H(t + 1) = {(1-\alpha )^{\sum\limits_{i = 0}^{t-1} {E(X(i))} }}{\pi _0}^{E(X(t))}\\ F(t + 1) = 1-{(1 - \alpha )^{\sum\limits_{i = 0}^{t - 1} {E(X(i))} }}{\pi _0}^{E(X(t))} \end{array} \right. $ | (11) |
对于阈值概率, 结合式(6)和式(8), 有:
| $ \text{E}(X(t)) = \left\{ \begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t = 0\\ N-(N-1){\pi _0}{(1-\alpha )^{t - 1}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;1 \le t < h\\ N - (N - 1){\pi _0}{(1 - \alpha )^{h - 2}}(1 - p\alpha )\;\;\;\;t \ge h \end{array} \right. $ | (12) |
根据定理1, 可以得出最优阈值概率。
定理 1 最优阈值h*存在。
证明:给定两个阈值h1 < h2, 其对应的期望值为Eh1(X(t))和Eh2(X(t)), 根据式(12)可知, Eh1(X(t))=Eh2(X(t)), t < h1; Eh1(X(t)) < Eh2(X(t), t≥h1。根据文献[11]随机序列的定义, Eh1(X(t))和Eh2(X(t)都是随机序列, 进一步结合式(11)可知, Eh1(T) < Eh2(T), 所以F(T)是h的单调递增函数。结合式(12)可知E(X(t))及F(T)都是h的单调递增函数。最优阈值h*可以按下述过程得到:
1) h=1, sum=E(X(1)), 如果sum < δ, 转步骤2), 否则h*=h-1, 进一步根据式(12)可以得出p(h)的值;
2) h=h+1, sum=E(X(h)), 如果sum < δ, 转步骤2), 否则h*=h-1, 进一步根据式(12)可以得出p(h)的值。如果h=T+1, 则h*=T+1。
下面证明最优概率是阈值形式。在证明之前, 先给出随机序列的相关定理。
定理 2[9] 给定两个随机序列x1和x2, 则x1小于x2, 记作x1 <st x2, 如果它们满足x1(t)≤x2(t), t≥0;且至少存在一个常数c≥0, x1(t) < x2(t)。
设f(x)是随机序列x的函数, 如果两个随机变量x1 <st x2且f(x1) <f(x2), 则f(x)是随机序列x的递增函数。
定理 3 最优概率是阈值形式。
证明:显然, 发送概率是随机序列, 而E(X(t))是对应的随机函数, 令EPf(X(t))表示发送概率pf对应的E(X(t))。给定两个发送概率p1和p2, 其在第t个时隙对应的值分别为p1(t)和p2(t)。存在一个常数c, 满足:t≠c, p1(t)=p2(t), t=c, p1(t) > p2(t), 0 < c≤T。从定理3可知p2 <st p1。下面证明E(X(t))是发送概率的递增函数。以ζi(t)代表节点i从时刻0到第t个时隙是否得到消息的指示变量, 为1则指已经得到消息; 为0则表示没有得到消息, 因此有:
| $ {\zeta _i}(t) = {\zeta _i}(t-1) + (1-{\zeta _i}(t-1)){\tau _i}(t) $ | (13) |
式中, 参数τi(t)代表节点i在第t个时隙是否得到消息的指示量。值得注意的是, 该参数的取值与节点在此之前是否得到消息无关。因此对应发送策略p1满足:
| $ p({\tau _i}(t) = 1) = {p_{iS}}(t){p_1}(t) $ | (14) |
式中, piS(t)代表节点i与S在第t个时隙是否相遇, 它只与节点运动规律有关, 而与发送概率无关。因此, 对应发送策略p2有:
| $ p({\tau _i}(t) = 1) = {p_{iS}}(t){p_2}(t) $ | (15) |
对式(13)取期望, 可以得到:
| $ E({\zeta _i}(t)) = E({\zeta _i}(t-1)) + (1-E({\zeta _i}(t-1)))p({\tau _i}(t) = 1) $ | (16) |
进一步有:
| $ E(X(T)) = \sum\limits_{i = 1}^N {E({\zeta _i}(T))} $ | (17) |
结合式(14)~式(17), 就可以知道E(X(t))是发送概率的单调递增函数。下面对定理进行证明。
假设最优阈值概率为p1, 其对应的阈值为h*, 且满足t < h*, p(t)=1, t=h*, p(t)=p, h* < t≤T, p(t)=0。当h*=T+1时, 发送概率总为1, 因此是最优概率。下面讨论h*≤T的情形, 给定另一个不同于p1的发送策略p2。假设存在常数c≤h*, 且满足p1(t)≥p2(t), t < c; p1(c) > p2(c); p1(t)≥p2(t), c < t≤h*。则发送概率在[0, c]时隙内满足p2≤st p1, [c, h*]时隙内满足p2 <st p1。
因此有EP2(X(t))≤EP1(X(t)), 0≤t < c。当c≤t≤h*时, 有EP2(X(t)) < EP1(X(t))。当t > h*时, 根据定理2, EP1(X(t))已经达到最大值, 因此EP2(X(t))≤EP1(X(t))同样成立。根据式(11), 可知最优阈值概率p1优于p2。假设常数c不存在, 则满足p1(t)=p2(t), t≤h*, 且至少存在一个值h1 > h*且满足p1(t)=0 < p2(t); 否则p2=stp1。显然, 此时p2 > stp1, 由于E(X(t))是发送概率的单调递增函数, 结合定理1, 则有EP2(X(h1)) > EP1(X(h1)) > δ。这违背了约束条件, 因此最优阈值概率始终是最优概率。
4 性能分析 4.1 仿真实验首先, 采用机会网络仿真平台(opportunistic network environment simulator, ONE)验证理论模型的正确性。因为采样周期越长, 连接失败及短连接时间的边消失的概率就越大[15], 这要求数据集具有较短的采样周期, 本文选用Rollernet数据集[16], 其采样周期约为12 s, 比传统的Reality Mining[17]的600 s及Infocom 2005[18]的120 s都要短。利用前3 000 s的数据, 并且选取60个节点, 连接平均持续时间为26.18 s, 节点平均度为4.75, 由此可以得到α=0.05, β=0.57。如图 2所示, 令T从1增加到10, 分别给出了δ=10和5时的结果。
 |
| 图2 实验与理论结果比较 |
从图 2可以看出, 理论结果与实验结果非常接近。当δ=10时, 平均误差为3.87%;δ=5时, 平均误差为3.26%。这说明本文模型非常精确。下面不进行过多的仿真验证, 只是通过数值结果对模型进行深入探讨。
4.2 性能评估下面通过数值结果来说明最优策略是阈值策略, 且利用仿真试验中的数据集。首先针对消息最大生存期T的变化进行探讨, 假设T从1增加到20, 且令δ=10。为了说明阈值策略的优越性, 给出了随机策略所对应的理论结果。随机策略是指在每一步信息源都从[0, 1]范围内随机选择发送概率。同样也给出了p(t)恒为1时的结果, 实际上此时无能量限制, 信息源始终以概率1发送。
从图 3可以看出最优阈值概率明显优于随机概率, 且与无能量限制的时候非常接近, 只在中间部分有一定的差别。这是因为当消息生存期较小时, 最优阈值h*几乎等于T, 即信息源始终以概率1发送; 当T较大时, 即使最优阈值h*小于T, 由于有充足的时间来完成传输, 其性能同样接近与发送概率恒为1的时候。但当T处于中间位置时, 最优阈值h*小于T, 因此中转节点得到消息的概率较小, 且由于消息生存期不大, 没有充足的时间来完成传输, 此时最优阈值概率会稍小于无能量限制的情形。
 |
| 图3 消息生命周期的影响 |
下面使最大能量δ从1增加到20, 且固定T=10, 可以得到如图 4所示曲线。
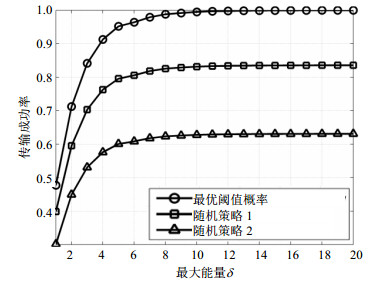 |
| 图4 最大能量的影响 |
图 4显示最优阈值策略明显优于其他策略。由于DTN网络通信的不可靠性, 传输延迟可能比较大, 所以DTN网络路由的主要指标就是尽可能提高传输成功率。但传输成功率的提高往往需要较多的副本, 从而消耗更多的能量。下面探讨对于不同的传输成功率所消耗的能量。假设传输成功率从10%增加到100%, 数值结果如图 5所示。
 |
| 图5 最小能量消耗 |
图 5显示出随着传输成功率的增加, 最小能量不断增加。此外, 如果消息的有效期较长, 则也可以用较少的能量来满足需要。
5 结论利用Edge-Markovian模型描述DTN中节点之间的连接关系, 并研究了能量约束条件下two-hop算法的最优控制问题。首先通过离散时间Markov过程对算法的消息传播过程进行建模, 在此基础上证明了最优发送概率必须服从阈值形式, 并且给出了计算最优阈值策略的定理。仿真实验证明了模型的正确性, 数值结果说明最优阈值概率优于随机概率。
| [1] |
FALL K. A delay-tolerant network architecture for challenged internets[C]//Proceedings of the 2003 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications. [S. l. ]: ACM, 2003.
|
| [2] |
ZHANG H, SHEN H, TAN Y. Optimal energy balanced data gathering in wireless sensor networks[C]//Parallel and Distributed Processing Symposium. California, USA: IEEE, 2007.
|
| [3] |
SPYROPOULOS T, PSOUNIS K, RAGHAVENDRA C. Spray and wait: an efficient routing scheme for intermittently connected mobile networks[C]//Proceedings of the 2005 ACM SIGCOMM Workshop on Delay-tolerant Networking. [S. l. ]: ACM, 2005.
|
| [4] |
SPYROPOULOS T, PSOUNIS K, RAGHAVENDRA C. Efficient routing in intermittently connected mobile networks:the multiple-copy case[J].
IEEE/ACM Transactions on Networking, 2008, 16(1): 77–90.
DOI:10.1109/TNET.2007.897964 |
| [5] |
PICU A, SPYROPOULOS T. Distributed stochastic optimization in opportunistic networks: the case of optimal relay selection[C]//Proceedings of the 5th ACM Workshop on Challenged Networks. [S. l. ]: ACM, 2010: 21-28.
|
| [6] |
MTIBAA A, MAY M, DIOT C, et al. Peoplerank: Social opportunistic forwarding[C]//2010 Proceedings of the INFOCOM. San Diego, CA, USA: IEEE, 2010.
|
| [7] |
BALASUBRAMANIAN A, LEVINE B, VENKATARAMANI A. Replication routing in DTNs:a resource allocation approach[J].
IEEE/ACM Transactions on Networking (TON), 2010, 18(2): 596–609.
DOI:10.1109/TNET.2009.2036365 |
| [8] |
GAO W, CAO G. User-centric data dissemination in disruption tolerant networks[C]//Proceedings of the INFOCOM. Shanghai: IEEE, 2011.
|
| [9] |
ALTMAN E, NEGLIA G, De PELLEGRINI F, et al. Decentralized stochastic control of delay tolerant networks[C]//Proceedings of the 30th INFOCOM. Rio de Janeiro: IEEE, 2009: 1134-1142.
|
| [10] |
LI Y, JIANG Y, JIN D, et al. Energy-efficient optimal opportunistic forwarding for delay-tolerant networks[J].
IEEE Transactions on Vehicular Technology, 2010, 59(9): 4500–4512.
DOI:10.1109/TVT.2010.2070521 |
| [11] |
DE PELLEGRINI F, ALTMAN E, BASCAR T. Optimal monotone forwarding policies in delay tolerant mobile ad hoc networks with multiple classes of nodes[C]// Proceedings of the 8th International Symposium on Modeling and Optimization in Mobile, Ad hoc and Wireless Networks(WiOpt). [S. l. ]: IEEE, 2010: 497-504.
|
| [12] |
ALTMAN E, BAŞAR T, KAVITHA V. Adversarial control in a delay tolerant network[J].
Lecture Notes in Computer Science, 2010(6442): 87–106.
|
| [13] |
CLEMENTI A, MACCI C, MONTI A, et al. Flooding time of edge-Markovian evolving graphs[J].
SIAM Journal on Discrete Mathematics, 2010, 24(4): 1694–1712.
DOI:10.1137/090756053 |
| [14] |
WHITBECK J, CONAN V, DIAS DE AMORIM M. Performance of opportunistic epidemic routing on edge-markovian dynamic graphs[J].
IEEE Transactions on Communications, 2011, 59(5): 1259–1263.
DOI:10.1109/TCOMM.2011.020811.090163 |
| [15] |
KER NEN A, OTT J, K RKK INEN T. The one simulator for DTN protocol evaluation[C]//Proceedings of the 2nd International Conference on Simulation Tools and Techniques. [S. l. ]: ACM, 2009.
|
| [16] |
TOURNOUX P U, Leguay J, Benbadis F, et al. The accordion phenomenon: Analysis, characterization, and impact on DTN routing[C]//Proceedings of the INFOCOM. [S. l. ]: IEEE, 2009: 1116-1124.
|
| [17] |
EAGLE N, PENTLAND A. Reality mining:Sensing complex social systems[J].
Personal and Ubiquitous Computing, 2006, 10(4): 255–268.
DOI:10.1007/s00779-005-0046-3 |
| [18] |
CHAINTREAU A, HUI P, CROWCROFT J, et al. Impact of human mobility on opportunistic forwarding algorithms[J].
IEEE Transactions on Mobile Computing, 2007, 6(6): 606–620.
DOI:10.1109/TMC.2007.1060 |
 2015, Vol. 44
2015, Vol. 44
