MIMO雷达相比于传统雷达有许多优势[1, 2, 3],如具有更高的角分辨率和多普勒分辨率等。当MIMO雷达发射正交信号[4, 5, 6, 7],发射模式和接收模式均可进行阵列处理,在接收端通过匹配滤波进行信号提取,提取到的信号可用于提高杂波的空间分辨率。利用不同发射天线和不同接收天线的相位偏差可构成一个新的虚拟阵列导向矢量,合理设计天线位置,MIMO雷达利用少量的天线就可获得一个非常长的严格采样的导向矢量数组[8]。
MIMO雷达使用稀疏阵列可避免旁瓣带来的不利影响[9]。但设置成稀疏阵列需要更大空间,制约了在机载雷达上的很好应用,且发射和接收不能使用相同天线,增加了成本。若使用紧凑阵列则可以地解决这些问题。本文利用新的算法使用紧凑阵列获得比传统波束形成方案更窄的主波束。
1 MIMO雷达信号模型假设有${N_{\rm{T}}}$个发射单元,间隔均为${d_{\rm{T}}}$,有${N_{\rm{R}}}$个接收单元,间隔均为${d_{\rm{R}}}$。采用单站式MIMO雷达,在每个发射单元,一个相关处理间隔发射脉冲的个数为L个。假设发射信号相互正交,系统内部没有杂波干扰,雷达系统平台的运动速度为$v$[10]。发射天线和接收天线有相同的方位角$\theta $和俯仰角$\varphi $。设${N_{\rm{T}}}$=${N_{\rm{R}}}$=$N$, ${d_{\rm{T}}}$=${d_{\rm{R}}}$=$d$=$\lambda /2$,$\lambda $为波长。在每个脉波重复间隔(PRI)${T_{\rm{r}}}$,系统发射波束集合为:
| $s{(}t{)} = {[{s_1}(t),{s_2}(t), \cdots ,{s_{{N_{\rm{T}}}}}(t)]^{\rm{T}}}$ | (1) |
${s_{{n_t}}}(t)({n_t} = 1,2, \cdots ,{N_{\rm{T}}})$是第${n_t}$个单元的发射信号且相互正交。 假设发射信号是窄带,即可忽略脉冲中的多普勒相移。对于第$l$个脉冲,在第${n_r}$个接收单元上来自所有距离环上的杂波片[11]的回波为:
| ${{y}_{{n_r}}} = \int\limits_{ - {\rm{\pi }}/2}^{{\rm{\pi }}/2} {\sum\limits_{{n_t} = 1}^{{N_{\rm{T}}}} {\xi (\theta ){{s}_{{n_t}}}{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}{f_s}(({n_t} - 1)\gamma + ({n_r} - 1))}}{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}{f_d}(l - 1)}}{\rm{d}}\theta } } $ | (2) |
式中,$\gamma = {d_{\rm{T}}}/{d_{\rm{R}}}$;${f_d} = 2v\sin \theta \cos \varphi \cdot {T_r}/\lambda $是移动平台的归一化多普勒频率;${f_s} = {d_{\rm{R}}}\sin \theta \cos \varphi /\lambda $是空间频率;$\xi (\theta )$是在$\theta $处的反射系数。假设${d_{\rm{R}}}$设置合理,保证$ - 0.5 \le {f_s} \le 0.5$,从而避免空间频率混叠。
本文假设发射导向矢量和接收导向矢量分别为:
| ${v_{\rm{T}}}(\theta ) = {[1,{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}\gamma {f_s}}}, \cdots ,{e^{{\rm{j}}2{\rm{\pi }}\gamma ({N_{\rm{T}}} - 1){f_s}}}]^{\rm{T}}}$ | (3) |
| ${v_{\rm{R}}}(\theta ) = {[1,{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}{f_s}}}, \cdots ,{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}({N_{\rm{R}}} - 1){f_s}}}]^{\rm{T}}}$ | (4) |
定义多普勒矢量为:
| ${v_D} = {[1,{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}{f_d}}}, \cdots ,{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}(L - 1){f_d}}}]^{\rm{T}}}$ | (5) |
对于第$l$个脉冲,接收单元的杂波回声为:
| ${Y_l} = \int\limits_{\theta = - {\rm{\pi }}/2}^{{\rm{\pi }}/2} {\xi (\theta ){{\rm{e}}^{{\rm{j}}2{\rm{\pi }}(l - 1){f_d}}}{v_R}(\theta )v_{\rm{T}}^{\rm{T}}(\theta )s{\rm{d}}\theta } $ | (6) |
式中,${Y_l} \in {C^{{N_{\rm{R}}} \times 1}}$。接收端信号处理是为了分离不同信号的相对时间延迟特性,从而为后续处理提供信号向量。每个接收到的信号包含所有发射波形,设${s^{\rm{H}}}$为接收端的滤波器组,有:
| ${X_l} = {Y_l}{s^{\rm{H}}}$ | (7) |
式中,${X_l} \in {C^{{N_{\rm{R}}} \times {N_{\rm{T}}}}}$。使用向量形式保持第$l$个脉冲的过滤杂波数据:
| ${x_l} = \int\limits_{ - {\rm{\pi }}/2}^{{\rm{\pi }}/2} {\xi (\theta ){{\rm{e}}^{{\rm{j}}2{\rm{\pi }}(l - 1){f_d}}}{v_{\rm{R}}}(\theta ) \otimes {v_{\rm{T}}}(\theta ){\rm{d}}\theta } $ | (8) |
式中,${x_l} \in {C^{{N_{\rm{R}}}{N_{\rm{T}}} \times 1}}$;“$ \otimes $”表示Kronecker积。距离环被分为${N_{\rm{C}}}$\left( {{N_{\rm{C}}} > > {N_{\rm{T}}}{N_{\rm{R}}}L} \right)$个杂波片,那么第$l$个脉冲的杂波数据分离形式为:
| ${x_l} = \sum\limits_{i = 1}^{{N_{\rm{C}}}} {\xi ({\theta _i}){{\rm{e}}^{{\rm{j}}2{\rm{\pi }}(l - 1){f_{d,i}}}}{v_{\rm{R}}}({\theta _i}) \otimes v_{\rm{T}}^{}({\theta _i})} $ | (9) |
式中,${f_{d,i}} = 2v{T_r}\sin {\theta _i}\cos \varphi /\lambda $。通常$\xi ({\theta _i})$定义为零均值、方差为$\sigma _i^2$的独立复高斯随机变量。整个杂波回波可以被定义为:
| $X = [{x_1},{x_2}, \cdots ,{x_L}] \in {C^{{N_{\rm{T}}}{N_{\rm{R}}} \times L}}$ | (10) |
然后将第L个脉冲的整个杂波回波保存为向量形式:
| $x = \sum\limits_{i = 1}^{{N_C}} {\xi ({\theta _i}){v_{\rm{D}}}({\theta _i}) \otimes {v_{\rm{R}}}({\theta _i}) \otimes {v_{\rm{T}}}({\theta _i})} \in {C^{{N_{\rm{T}}}{N_{\rm{R}}}L \times 1}}$ | (11) |
式中,${v_{\rm{D}}}({\theta _i}) = {[1,{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}{f_{d,i}}}}, \cdots ,{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}(L - 1){f_{d,i}}}}]^{\rm{T}}}$;${f_{d,i}} = $ $2v\sin {\theta _i}\cos \varphi \cdot {T_r}/\lambda $。
2 更窄主瓣波束形成方法接收波束通过相位变换叠加处理来利用天线阵元的输出实现延迟叠加波束形成,从而实现数字合成[12]。MIMO雷达的正交信号可在接收端通过匹配滤波进行提取,提高杂波的空间分辨率[13]。维数为${N_{\rm{T}}}{N_{\rm{R}}}$的阵列导向矢量可以等效为发射导向矢量与接收导向矢量的卷积。假设${N_{\rm{R}}} = {N_{\rm{T}}} = N$,对于波束形成,只考虑等间距的线性阵列。已经证明在匹配滤波之后实际获得的天线波束相比于对应的传统相控雷达具有相同的天线增益和空间分辨率。同时数字滤波器的系数矢量按如下方式设置:
| $w = \kappa s_0^*$ | (12) |
式中,$\kappa $满足归一化的要求;${s_0}$是来自期望方向${\theta _0}$处的目标信号,有:
| ${s_0} = {v_{\rm{R}}}({\theta _0}) \otimes v_{\rm{T}}^{}({\theta _0})$ | (13) |
通过式(12)和式(13),可以获得具有最大信噪比(SNR)的滤波器输出。而收发波束的指向可通过数字滤波器获得。将式(12)改写为:
| $\begin{array}{c} w = \kappa s_0^* = \kappa {({v_{\rm{R}}}({\theta _0}) \otimes v_{\rm{T}}^{}({\theta _0}))^*} = \\ ({\kappa _1}v_{\rm{R}}^*({\theta _0})) \otimes ({\kappa _2}v_{\rm{T}}^*({\theta _0})) = {w_{\rm{R}}} \otimes {w_{\rm{T}}} \end{array}$ | (14) |
式中,$\kappa = {\kappa _1}{\kappa _2}$,均为常数;${w_{\rm{T}}}$为发射波束的数字滤波器的系数向量;${w_{\rm{R}}}$为接收波束的权向量。利用式(12)和式(14)中的最佳滤波器,通过虚拟收发波束形成,可获得虚拟天线增益:
| $\left| {G(\theta ,{\theta _0})} \right| = \left| {{w^{\rm{T}}}({\theta _0})s(\theta )} \right| = \kappa \left| {\sum\limits_{n = 1}^{{N_{\rm{R}}}} {{{\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}{f_{s,0}}}}{{\rm{e}}^{{\rm{j}}2\pi {f_{s,i}}}}} } \right|\left| {\sum\limits_{n = 1}^{{N_{\rm{T}}}} {{{\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}\gamma {f_{s,0}}}}{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}\gamma {f_{s,i}}}}} } \right|$ | (15) |
上式为离散傅里叶变换(DFT)[14]的形式。本文设置${d_{\rm{R}}} = {d_{\rm{T}}} = d$,$d/\lambda = 0.5$,${N_{\rm{R}}} = {N_{\rm{T}}} = N$,可得:
| $\left| {G(\theta ,{\theta _0})} \right| = \frac{1}{{{N^2}}}{\left| {\frac{{\sin \left[ {N{\rm{\pi }}\frac{d}{\lambda }\cos \varphi (\sin \theta - \sin {\theta _0})} \right]}}{{\sin \left[ {{\rm{\pi }}\frac{d}{\lambda }\cos \varphi (\sin \theta - \sin {\theta _0})} \right]}}} \right|^2}$ | (16) |
从式(15)和式(16)知,$\left| {G(\theta ,{\theta _0})} \right|$可以看做是两个长度均为N的方波离散傅里叶变换(DFT)的积。图 1阐述了一维均匀线性阵列导向矢量的卷积性质。
MIMO雷达的虚拟收发波束形成可以看作是两个方波的离散傅里叶变换的积。两个方波的卷积是三角波,其长度为$2N - 1$,如图 1所示。图 1中的振幅是具有相同的相位中心的阵元的数量。根据傅里叶理论,发射波束的主瓣宽度被扩宽了。为了更明确这一点,改写MIMO雷达接收端经过匹配滤波后的信号的矩阵如下:
| $\begin{array}{c} {v_{\rm{R}}} \otimes v_{\rm{T}}^{\rm{T}} = \\ \;\left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{{\rm{j}}(1 - 1){f_s}}}}&{{{\rm{e}}^{{\rm{j}}(1 - 1){f_s} + (2 - 1)\gamma {f_s}}}}&{...}&{{{\rm{e}}^{{\rm{j}}(1 - 1){f_s} + ({N_{\rm{T}}} - 1)\gamma {f_s}}}}\\ {{{\rm{e}}^{{\rm{j}}(2 - 1){f_s}}}}&{{{\rm{e}}^{{\rm{j}}(2 - 1){f_s} + (2 - 1)\gamma {f_s}}}}&{}&{{{\rm{e}}^{{\rm{j}}(2 - 1){f_s} + ({N_{\rm{T}}} - 1)\gamma {f_s}}}}\\ \vdots & \vdots &{}& \vdots \\ {{{\rm{e}}^{{\rm{j}}({N_{\rm{R}}} - 1){f_s}}}}&{{{\rm{e}}^{{\rm{j}}({N_{\rm{R}}} - 1){f_s} + (2 - 1)\gamma {f_s}}}}&{...}&{{{\rm{e}}^{{\rm{j}}({N_{\rm{R}}} - 1){f_s} + ({N_{\rm{T}}} - 1)\gamma {f_s}}}} \end{array}} \right] \end{array}$ | (17) |
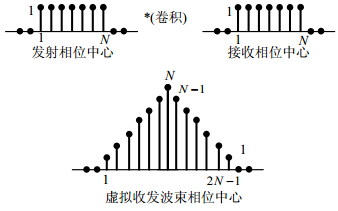 |
| 图 1 导向矢量的卷积性质 |
式中,$\gamma = {d_{\rm{T}}}/{d_{\rm{R}}}$,${v_{\rm{T}}}$为发射导向矢量;${v_{\rm{R}}}$为接收导向矢量,它们均已在式(3)和式(4)中进行了定义。如果考虑到噪声,则匹配滤波后的输出信号为:
| $x = {v_{\rm{R}}} \otimes v_{\rm{T}}^{\rm{T}} + n$ | (18) |
式中,$n \in {C^{{N_R} \times {N_T}}}$。本文将阵列布置为紧凑阵列, $\gamma $=1, 式(17)可以被改写为:
| ${v_{\rm{R}}} \otimes v_{\rm{T}}^{\rm{T}} = \left[ {\begin{array}{*{20}{c}} 1&{{{\rm{e}}^{{\rm{j}}{f_s}}}}&{...}&{{{\rm{e}}^{{\rm{j}}(N - 1){f_s}}}}\\ {{{\rm{e}}^{{\rm{j}}{f_s}}}}&{{{\rm{e}}^{{\rm{j}}2{f_s}}}}&{}&{{{\rm{e}}^{{\rm{j}}N{f_s}}}}\\ \vdots & \vdots &{}& \vdots \\ {{{\rm{e}}^{{\rm{j}}\left( {N - 1} \right){f_s}}}}&{{{\rm{e}}^{{\rm{j}}N{f_s}}}}&{...}&{{{\rm{e}}^{{\rm{j}}\left( {2N - 1} \right){f_s}}}} \end{array}} \right]$ | (19) |
可以发现式(19)中有很多元素相等,如图 2所示。
 |
| 图 2 矩阵中的相等元素 |
根据离散傅里叶变换的性质,相同长度的方波主瓣比三角波更窄。在直觉上可以通过权值反转变换,将三角波变换为方波,如图 3所示。
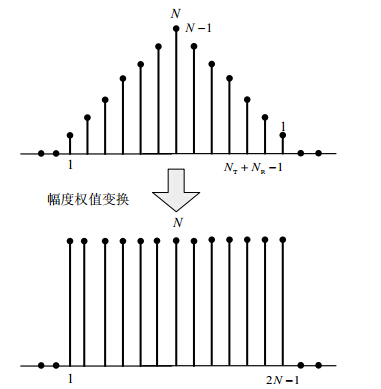 |
| 图 3 权值反转过程 |
与式(18)或式(19)对应的权值转换矩阵为:
| $D = \left[ {\begin{array}{*{20}{c}} N&{\frac{N}{2}}&{...}&{\frac{N}{{N - 1}}}&1\\ {\frac{N}{2}}&{\frac{N}{3}}&{...}&1&{\frac{N}{{N - 1}}}\\ \vdots & \vdots &{...}& \vdots & \vdots \\ {\frac{N}{{N - 1}}}&1&{...}&{\frac{N}{3}}&{\frac{N}{2}}\\ 1&{\frac{N}{{N - 1}}}&{...}&{\frac{N}{2}}&N \end{array}} \right]$ | (20) |
$d = {\rm{stack(}}D{\rm{)}}$。对应于虚拟收发波束的数字滤波器系数向量为:
| ${w_{{\rm{new}}}} = w \odot d$ | (21) |
如果使用窗函数,由于权向量${w_{{\rm{new}}}}$与期望信号$s$不能完美匹配,所以SNR有一定的损失。根据式(18)中的一维波束形成加窗的信噪比损失因子,定义虚拟收发波束加窗的信噪比损失因子为${\eta _{{\rm{eff}}}}$,它是加窗后的信噪比$({\rm{SN}}{{\rm{R}}_{{\rm{tap}}}})$与最优输出信噪比$({\rm{SN}}{{\rm{R}}_{{\rm{opt}}}})$之比值。为便于计算,${\eta _{{\rm{eff}}}}$通常定义为:
| ${\eta _{{\rm{eff}}}} = \frac{{{\rm{SN}}{{\rm{R}}_{{\rm{tap}}}}}}{{{\rm{SN}}{{\rm{R}}_{{\rm{opt}}}}}} = \frac{{{{\left| {w_{{\rm{new}}}^{\rm{T}}{s_0}} \right|}^2}}}{{{N^2}}}$ | (22) |
式中,${s_0}$是期望信号,其定义如式(13)。考虑锥形的情况,${w_{{\rm{new}}}} = s_0^* \odot d$,保证单位增益约束为$w_{{\rm{new}}}^{\rm{H}}w_{{\rm{new}}}^{} = 1$,${\rm{vec(}}t{\rm{)}}$必须满足:
| $\begin{array}{c} {{w'}_{{\rm{new}}}}w_{{\rm{new}}}^{} = {(s_0^* \odot d)^{\rm{H}}}(s_0^* \odot d) = \\ {({s_0} \odot s_0^*)^{\rm{H}}}({d^*} \odot d) = \left\| d \right\|_2^2 = 1 \end{array}$ | (23) |
式中,${\left\| d \right\|_2}$表示通用的欧几里德向量范数。将${w_{{\rm{new}}}} = s_0^* \odot d$代入式(23),得:
| ${\eta _{{\rm{eff}}}} = \frac{{{{\left| {{{(s_0^* \odot d)}^{\rm{T}}}{s_0}} \right|}^2}}}{{{N^2}}} = \frac{{{{\left| {{{(s_0^* \odot {s_0})}^{\rm{H}}}d} \right|}^2}}}{{{N^2}}} = \frac{{\left\| d \right\|_1^2}}{{{N^2}}}$ | (24) |
式中,$\left\| d \right\|_1^2$表示${L_1}$的范数。
对于四阵元的收发波束形成,${\left\| d \right\|_1}$=3.537,代入式(24),得${\eta _{{\rm{eff}}}}$=0.781 9,即为-1.068 5 dB。
图 4为信噪比损失因子${\eta _{{\rm{eff}}}}$与阵元数目变化关系。从图 4可以发现,随着阵元数目的增加,${\eta _{{\rm{eff}}}}$的减小速率将会降低。对应于16阵元、32阵元、80阵元,其${\eta _{{\rm{eff}}}}$分别为-2.515、-3.193、-3.998 dB。更窄的主瓣会带来SNR的损失,可以根据需要合理选择。更窄的波束可以提高角分辨率和多普勒分辨率,抑制来自目标的主瓣杂波干扰。通常,接收端的剩余旁瓣会带来足够的干扰掩盖期望的返回信号,在波束形成中是不允许存在过高的旁瓣。本文也可以使用切比雪夫窗函数。直接将切比雪夫窗函数式(21)写为:
| ${w_{{\rm{new}}}} = w \odot d \odot ({w_{{\rm{ch}},N}} \otimes {w_{{\rm{ch}},N}})$ | (25) |
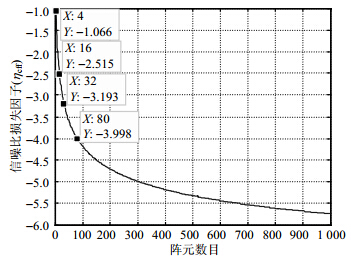 |
| 图 4 信噪比损失因子${\eta _{{\rm{eff}}}}$与阵元数目变化关系 |
将式(25)对应的加窗方式命名为方式1。根据式(20)中提出的加权方式,该加权方式将会改变切比雪夫窗函数的形状,旁瓣可能得不到有效地抑制。可以通过改变切比雪夫窗函数来克服该问题。根据图 4描述的相位中心,将${w_{{\rm{ch}},2N - 1}}$扩展到${N^2}$个点,${w_{{\rm{ch}},2N - 1}}$是$2N - 1$个点的切比雪夫窗函数的权向量。即由相同相位的匹配滤波器有相同的切比雪夫窗权系数为:
| $\begin{array}{*{20}{c}} {{w_{{\rm{ch}},{N^2}}} = [{w_{{\rm{ch}},2N - 1}}(1)\; \cdots \;{w_{{\rm{ch}},2N - 1}}(N)\;\;{w_{{\rm{ch}},2N - 1}}(2)\; \cdots }\\ {{w_{{\rm{ch}},2N - 1}}(N + 1)\; \cdots \;{w_{{\rm{ch}},2N - 1}}(N)\; \cdots \;{w_{{\rm{ch}},2N - 1}}(2N - 1){]^{\rm{T}}}} \end{array}$ | (26) |
将式(26)对应的加窗方式命名为方式2,将式(26)代入式(25),替换${w_{{\rm{ch}},N}} \otimes {w_{{\rm{ch}},N}}$:
| ${w_{{\rm{new}}}} = w \odot d \odot {w_{{\rm{ch}},{N^2}}}$ | (27) |
可以得到虚拟天线增益为:
| $\left| {G(\theta ,{\theta _0})} \right| = \left| {w_{{\rm{new}}}^{\rm{T}}({\theta _0})s(\theta )} \right|$ | (28) |
为了评估减小的主瓣杂波,虚拟收发波束形成被配置成串联T-S模式。时间权向量首先在每个天线通道的每个匹配滤波器的输出上进行计算,有:
| ${y_l} = Xw_{t,l}^{\rm{H}}$ | (29) |
式中,${w_{t,l}}$是对应于离散傅里叶变换系数的权向量;下标$l$表示第$l$个多普勒通道;下标$t$表示时域。多普勒处理器的输出结果在空域中进行进一步处理以获得检验统计量:
| $\eta = w_s^{\rm{H}}{y_l}$ | (30) |
式中,下标$s$表示时域,有:
| ${y_l} = {[{y_{l,1}}\;{y_{l,2}} \cdots \;{y_{l,{N_{\rm{T}}}{N_{\rm{R}}}}}]^{\rm{T}}}$ | (31) |
通过渐变模式得到的更窄的主瓣波束有很多优势,比如提升角分辨率和多普勒分辨率,具有更尖锐的机载雷达杂波凹口。这些优势都可以应用于机载雷达对地面低速运动目标的检测。通常用单阵元、单脉冲的SINR值来衡量空时处理算法的性能。${\rm{SIN}}{{\rm{R}}_{{\rm{in}}}}$作为单阵元、单脉冲的SINR。通常情况下杂波和干扰比较强,所以${\rm{SIN}}{{\rm{R}}_{{\rm{in}}}}$相对是一个非常小的量。SINR的提高因子${\rm{I}}{{\rm{F}}_{{\rm{SINR}}}}$被定义为:
| ${\rm{I}}{{\rm{F}}_{{\rm{SINR}}}}({f_d}) = \frac{{{\rm{SIN}}{{\rm{R}}_{{\rm{out}}}}({f_d})}}{{{\rm{SIN}}{{\rm{R}}_{{\rm{in}}}}}}$ | (32) |
${\rm{SIN}}{{\rm{R}}_{{\rm{out}}}}(\varpi )$在串联T-S模式下的配置为:
| ${\rm{SIN}}{{\rm{R}}_{{\rm{out}}}}({f_d}) = \frac{{{{\left| {w_s^{\rm{H}}{s_0}} \right|}^2}{{\left| {w_{t,l}^{\rm{H}}{s_{t,l}}({f_d})} \right|}^2}}}{{w_s^{\rm{H}}{R_l}w_s^{}}}$ | (33) |
式中,${s_{t,l}}({f_d})$是期望目标的多普勒导向矢量:
| ${s_{t,l}}({f_d}) = {\left[ {{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}\frac{{l \cdot 0}}{L}}}\;\;{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}\frac{{l \cdot 1}}{L}}}\; \cdots \;{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}\frac{{l \cdot (L - 1)}}{L}}}} \right]^{\rm{T}}}$ | (34) |
${R_l}$是第$l$个多普勒通道的协方差矩阵,有:
| ${R_l} = [{(I \otimes {w_{t,l}})^{\rm{H}}}R(I \otimes {w_{t,l}})] \in {C^{{N_{\rm{T}}}{N_{\rm{R}}} \times {N_{\rm{T}}}{N_{\rm{R}}}}}$ | (35) |
式中,$I$是单位矩阵;$R$是整个协方差矩阵,有:
| $R = E[x{x^{\rm{H}}}]$ | (36) |
考虑一八阵元发射接收阵列,${N_{\rm{T}}} = {N_{\rm{R}}} = $ $N = 8$,${d_{\rm{T}}} = {d_{\rm{R}}} = d = \lambda /2$,主瓣方向${\theta _0} = 0^\circ $,目标位于主瓣所在方向。载波频率为${f_0} = 1.2{\rm{ GHz}}$,脉冲重复频率${\rm{PRF}}$为2 000 Hz,一个相关处理间隔发射脉冲数为$M = 64$。雷达运动速度为$v = 125{\rm{ m/s}}$,对于每一个天线阵元,每一个脉冲内的${\rm{SNR = }} - {\rm{5 dB}}$,${\rm{CNR = 45 dB}}$。式(25)对应方式1的波束形成方式,式(27)中对应方式2的波束形成方式,以及只考虑在接收波束形成中使用30 dB切比雪夫加窗(方式3)的相控阵雷达波束。对比3种不同的波束形式如图 5所示。
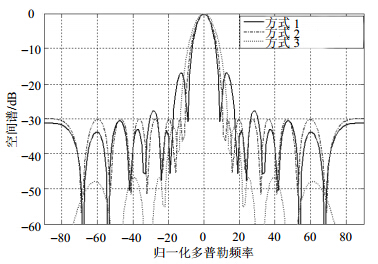 |
| 图 5 3种不同波束形成方式效果比较 |
由图 5可知,由于方式1的切比雪夫窗函数形式的改变并没能有效抑制旁瓣。而方式2的切比雪夫加窗过程由于采用虚拟的发射接收波束,旁瓣得到了有效的抑制。对于相控阵雷达系统,由于考虑到最大发射功率的要求,切比雪夫加窗只用在接收波束形成过程中,虽然旁瓣得到了抑制,但主瓣也相应的展宽了。相比于其他方法的信干噪比改善因子如图 6所示。为方便比较,在归一化多普勒频率处的最小的改善因子也被归一化为0 dB。
 |
| 图 6 不同波束形成方式的归一化SINR提升因子的比较 |
图 6中所加切比雪夫窗为30 dB,本文提出的基于渐变处理的波束形成方法主要在小多普勒频率范围优于没有进行渐变处理的波束形成方法,这一点对于检测低速运动目标非常有用。比如对于低速运动目标,在归一化多普勒频率为0.062 5时,新方法的信干噪比改善因子可以达到7.3 dB。没有进行切比雪夫加窗时,新方法的信干噪比改善因子比没有进行渐变处理时在旁瓣区域差,但可以通过简单地修正切比雪夫窗函数来克服不足。在小多普勒频率区域,用30 dB切比雪夫加窗形成的相控阵雷达接收波束效果比较差,特别是在归一化多普勒频率位于$( - 0.1,0.1)$时。通过上面的分析可知,波束主瓣宽度越窄,对低速目标的检测效果越好。
4 总 结本文提出的MIMO雷达匹配滤波器输出信号的幅度经过加窗处理之后,对低速运动物体的检测效果有一定程度的提高。通过本文所提出的加窗方式可以获得更窄的主瓣,显著提高杂波抑制效果,改善角度分辨率,提升探测低速运动目标性能,因此可以提高对低速运动物体的检测效果。对于其他阵元数目的MIMO雷达,采用该加窗方式之后检测效果类似。方便将该方式应用于级联时空处理。本文的方法也可以应用于其他波束域的STAP算法。这种新型加窗方式提高了对低速运动目标的检测效果,完善了MIMO雷达的性能,对于现代机载雷达具有重要意义。
| [1] | BROOKNER E,RAYTHEON C. MIMO radar demystified and where it makes sense to use[C]//Phased Array Systems&Technology. Waltham,USA: IEEE,2013. |
| [2] | MOO P W,ZHEN Ding. Tracking performance of MIMO radar for accelerating targets[J]. Signal Processing,2013,61(21): 5205-5216. |
| [3] | RANKIN G A,TIRKEL A Z,BUI L Q,et al. Radar imaging: Conventional and MIMO[C]//Communications and Electronic(ICCE). Hue,USA: IEEE,2012. |
| [4] | HE Qian,LEHMANN N H,BLUM R S,et al. MIMO radar moving target detection in homogeneous clutter[J]. IEEE Transactions on Aerospace and Electronic Systems,2010,46(3): 1290-1301. |
| [5] | 牛朝阳,张剑云. MIMO雷达正交波形集设计—线性调频-位编码混合波形[J]. 计算机工程与应用,2012,48(13): 133-137. NIU Zhao-yang,ZHANG Jian-yun. Orthogonal waveform set of hybird LFM and phase code for MIMO radar[J]. Computer Engineering and Application,2012,48(13): 133-137. |
| [6] | RABIDEAU D J. Non-adaptive multiple-input,multiple- output radar techniques for reducing clutter[J]. IET Radar Sonar Navig,2009,3(4): 304-313. |
| [7] | 杜晓林,王旭,苏涛,等. MIMO雷达正交相位编码信号的代数设计方法[J]. 西安电子科技大学学报(自然科学版),2014,41(2): 64-70. DU Xiao-lin,WANG Xu,SU Tao,et al. Orthogonal phase coding signal design for MIMO radar via an algebraic method[J]. Journal of Xidian University(Natural Science Edition),2014,41(2): 64-70. |
| [8] | CHEN Chun-yang,VAIDYANATHAN P P. Beamforming issues in modern MIMO radars with doppler[C]//The 40th Asilomar Coference on Signals,Systems and Computers. Pacific Grove,CA,USA: IEEE,2006. |
| [9] | FORSYTHE K W,BLISS D W. MIMO radar signal processing[M]. New York,USA: Wiley,2009. |
| [10] | DENG Hai,BRAHAM H. A virtual antenna beamforming (VAB) approach for radar systems by using orthogonal coding waveforms[J]. IEEE Transactions on Antennas and Propagation,2009,57(2): 425-435. |
| [11] | WANG Guo-hua,LU Yi-long. Clutter rank of mimo radar with a speical class of waveforms[C]//Waveform Diversity and Design Conference. Kissimmee,FL,USA: IEEE,2009. |
| [12] | MONDAL B,HEATH R W. Performance analysis of quantized beamforming MIMO systems[J]. IEEE Trans Signal Process,2006,54(12): 4753-4766. |
| [13] | CHEN Chun-yang,VAIDYANATHAN P P. MIMO radar space-time adaptive processing using prolate spheroidal wave functions[J]. IEEE Transactions on Signal Processing,2008,56(2): 623-635. |
| [14] | 周剑雄,石志广,吴京. 离散时间信号频域分析中的概念辨析[J]. 电气电子教学学报,2014,36(1): 49-51. ZHOU Jian-xiong,SHI Zhi-guang,WU Jing. Conceptual discrimination in frequency domain analysis of discrete time signals[J]. Journal of EEE,2014,36(1): 49-51. |
 2015, Vol. 44
2015, Vol. 44
