PCMA技术因能成倍地提高卫星频谱的利用效率,受到了广泛关注。由于在本地存储有自干扰信号的符号序列,因此只需对调制参数进行估计后就可重构自干扰信号波形并从接收混合信号中去除。在PCMA专利[1]中,参数估计是通过通信双方在正式通信前分别独自发送的一段训练序列进行的,需要进行握手且增加了系统时间开销。后续很多学者采用基于数据辅助的方法直接从混合信号中估计本地信号参数初始值,然后用迟早门进行跟踪[2],其中,定时估计利用传统的相关估计[3],频偏估计则应用Kay[4]、Fitz[5]、L&R[6]等经典算法。在经典算法基础上,考虑信道影响,文献[7]提出了联合信道频偏估计方法。文献[8]针对本地信号构建最大似然目标函数,提出了幅度、时延、相位的联合最大似然估计并进行三维寻优。上述方法的处理过程本质上仍是单信号模型下的求解,并未考虑混合信号模型。文献[9]给出了混合信号条件下联合定时估计算法,算法仅对定时偏差进行了联合估计且需预知混合信号功率比,实用性受到限制。
本文针对PCMA混合信号模型,构建了混合信号条件下最大似然目标函数,推导了混合信号频偏、相偏、信道联合估计表达式。利用单纯形法求频偏值,通过递归迭代求得其他估计量。算法估计性能逼近混合信号模型下CRB(Cramer-Rao)界,能适应频率选择性信道,计算机仿真验证了本文算法的有效性。
1 信号模型设接收信号的模型为:
| $\begin{array}{l} r(t) = s(t) + w(t) = {s_{\rm{1}}}(t) + {s_{\rm{2}}}(t) + w(t) = \\ {\rm{ }}{a_{\rm{1}}}\sum\limits_k {{a_{{\rm{1}},k}}{{\rm{e}}^{{\rm{j}}\left( {{\rm{\Delta }}{w_{\rm{1}}}t + {\varphi _{\rm{1}}}} \right)}}{g_{\rm{1}}}(t - k{T_{\rm{1}}} + {t_{\rm{1}}})} + \\ {\rm{ }}{a_{\rm{2}}}\sum\limits_k {{a_{{\rm{2}},k}}{{\rm{e}}^{{\rm{j}}\left( {{\rm{\Delta }}{w_{\rm{2}}}t + {\varphi _{\rm{2}}}} \right)}}{g_{\rm{2}}}(t - k{T_{\rm{2}}} + {t_{\rm{2}}})} + w(t) \end{array}$ | (1) |
式中,当$s(t)$是常规调制信号时,有${\alpha _1} \ne 0$,${\alpha _2} = 0$;${T_i}$是第$i$路信号符号周期;$\Delta {\omega _i}$是残余载波频偏;${\varphi _i}$是相偏;${\tau _i}$是定时偏移,假定$0 \le {\tau _i} < T$;${a_{i,k}}$是独立同分布的符号序列;$w(t)$为加性高斯白噪声;${g_i}(t)$是等效信道滤波器,包括成型、信道和匹配滤波。
对于同符号速率合作方PCMA通信,有${T_1} = {T_2} = T$,${g_1}(t) = {g_2}(t) = g(t)$,经符号速率采样,可得:
| $\begin{array}{l} r(n) = s(n) + w(n) = {s_1}(n) + {s_2}(n) + w(n) = \\ {\rm{ }}{\alpha _1}{{\rm{e}}^{{\rm{j}}\left( {2{\rm{\pi }}n{v_1} + {\varphi _1}} \right)}}\sum\limits_{k = 0}^{L - 1} {{a_{1,n - k}}g(kT + {\tau _1})} + \\ {\rm{ }}{\alpha _2}{{\rm{e}}^{{\rm{j}}\left( {2{\rm{\pi }}n{v_2} + {\varphi _2}} \right)}}\sum\limits_{k = 0}^{L - 1} {{a_{2,n - k}}g(kT + {\tau _2})} + w(n)\\ {\rm{ }}n = 0,1, \cdots ,N - 1 \end{array}$ | (2) |
式中,N为采样符号数;L为信道记忆长度;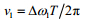 ,
,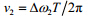 。对于训练序列
。对于训练序列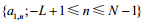 、$\{ {a_{2,n}}; - L + 1 \le n \le N - 1\} $,式(2)可描述为矩阵形式:
、$\{ {a_{2,n}}; - L + 1 \le n \le N - 1\} $,式(2)可描述为矩阵形式:
| ${\bf{r}} = {\alpha _1}{{\rm{e}}^{{\rm{j}}{\varphi _1}}}{\bf{\Gamma }}({v_1}){\bf{A}}{{\bf{g}}_1} + {\alpha _2}{{\rm{e}}^{{\rm{j}}{\varphi _2}}}{\bf{\Gamma }}({v_2})B{{\bf{g}}_2} + {\bf{w}}$ | (3) |
式中,${\bf{r}} = {[r(0),r(1), \cdots ,r(N - 1)]^{\rm{T}}}$;${\bf{\Gamma }}(v) = $ ${\rm{diag\{ }}1,{{\rm{e}}^{{\rm{j}}2{\rm{\pi }}v}},{{\rm{e}}^{{\rm{j4\pi }}v}}, \cdots ,{{\rm{e}}^{{\rm{j2\pi }}\left( {N - 1} \right)v}}{\rm{\} }}$;${{\bf{g}}_1} = [g({\tau _1}),g(T + {\tau _1}),$ $ \cdots ,g((L - 1)T + {\tau _1}){]^{\rm{T}}}$;${{\bf{g}}_2} = [g({\tau _2}),g(T + {\tau _2}), \cdots ,$ $g((L - 1)T + {\tau _2}){]^{\rm{T}}}$;${[A]_{i,j}} = {a_{1,i - j}}{\rm{, }}{[B]_{i,j}} = {a_{2,i - j}},$ $0 \le i \le N - 1,0 \le j \le L - 1$;噪声向量${\bf{w}} = {[w(0),w(1), \cdots ,w(N - 1)]^{\rm{T}}}$均值为0;协方差矩阵${{\bf{C}}_{\bf{w}}} = E[{\bf{w}}{{\bf{w}}^{\rm{H}}}] = \sigma _n^2{{\bf{I}}_N}$,${{\bf{I}}_N}$为单位阵;信噪比为$\frac{{{E_{\rm{s}}}}}{{{N_0}}} = \frac{{\sigma _{{s_1}}^2}}{{\sigma _n^2}}\frac{{{F_{\rm{s}}}}}{{{R_{\rm{s}}}}}$,$\sigma _{{s_1}}^2 = \frac{1}{N}\sum\limits_{n = 0}^{N - 1} {{{\left| {{s_1}(n)} \right|}^2}} $;信号功率比 ,其中,对于单倍符号采样$frac{{{F_{\rm{s}}}}}{{{R_{\rm{s}}}}} = 1$。
,其中,对于单倍符号采样$frac{{{F_{\rm{s}}}}}{{{R_{\rm{s}}}}} = 1$。
接收向量r的最大似然函数为:
| $\begin{array}{l} {\rm{ }}p({\bf{r}}\left| {{\alpha _1},{\theta _1},{v_1},{{\bf{g}}_1},{\alpha _2},{\theta _2},{v_2},{{\bf{g}}_2}} \right.) = \frac{1}{{{{({\rm{\pi }}\sigma _n^2)}^N}}} \times \\ \exp \left\{ { - \frac{1}{{\sigma _n^2}}{{\left\| {{\bf{r}} - {{\rm{e}}^{{\rm{j}}{\theta _1}}}{\alpha _1}{\bf{\Gamma }}({v_1}){\bf{A}}{{\bf{g}}_1} - {{\rm{e}}^{{\rm{j}}{\theta _2}}}{\alpha _2}{\bf{\Gamma }}({v_2}){\bf{B}}{{\bf{g}}_2}} \right\|}^2}} \right\} \end{array}$ | (4) |
令:${{\bf{h}}_1} = {{\rm{e}}^{{\rm{j}}{\theta _1}}}{\alpha _1}{{\bf{g}}_1}$,${{\bf{h}}_2} = {{\rm{e}}^{{\rm{j}}{\theta _2}}}{\alpha _2}{{\bf{g}}_2}$,取对数后,最大似然函数可描述为:
| $\ln \Lambda ({\bf{r}}\left| {{v_1},{{\bf{h}}_1},{v_2},{{\bf{h}}_2}} \right.) = - {\left\| {{\bf{r}} - {\bf{\Gamma }}({v_1}){\bf{A}}{{\bf{h}}_1} - {\bf{\Gamma }}({v_2}){\bf{B}}{{\bf{h}}_2}} \right\|^2}$ | (5) |
对h1求导并赋值为0,有:
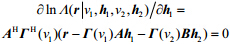
|
(6) |
可得:
| ${{\bf{\hat h}}_1} = {({{\bf{A}}^{\rm{H}}}{\bf{A}})^{ - 1}}{{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_1})({\bf{r}} - {\bf{\Gamma }}({v_2}){\bf{B}}{{\bf{h}}_2})$ | (7) |
将式(7)代入式(5),似然函数可表示为:
| $\ln \Lambda ({\bf{r}}\left| {{v_1},{v_2},{{\bf{h}}_2}} \right.) = - {\left\| {[{\bf{I}} - {\bf{C}}({v_1})][{\bf{r}} - {\bf{\Gamma }}({v_2}){\bf{B}}{{\bf{h}}_2}]} \right\|^2}$ | (8) |
式中,${\bf{C}}(v) = {\bf{\Gamma }}(v){\bf{A}}{({{\bf{A}}^{\rm{H}}}{\bf{A}})^{ - 1}}{{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}(v)$,将式(8)对h2求导并赋值为0,有:
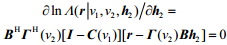
|
(9) |
可得:
| ${{\bf{\hat h}}_2} = {[{\bf{X}}{({v_1},{v_2})^{\rm{H}}}{\bf{X}}({v_1},{v_2})]^{ - 1}}{\bf{X}}{({v_1},{v_2})^{\rm{H}}}{\bf{r}}$ | (10) |
式中,${\bf{X}}({v_1},{v_2}) = [{\bf{I}} - {\bf{C}}({v_1})]{\bf{\Gamma }}({v_2}){\bf{B}}$,用${\bf{X}}$标识。
${\hat \theta _1} = \arg ({{\bf{\hat h}}_1})$,${\hat \theta _2} = \arg ({{\bf{\hat h}}_2})$,${\hat \alpha _1} = \left\| {{{{\bf{\hat h}}}_1}} \right\|$,${\hat \alpha _2} = \left\| {{{{\bf{\hat h}}}_2}} \right\|$,
将${{\bf{\hat h}}_2}$代入式(8),似然目标函数可表示为:
| $\ln \Lambda ({\bf{r}}\left| {{v_1},{v_2}} \right.) = - {{\bf{r}}^{\rm{H}}}{\bf{r}} + {{\bf{r}}^{\rm{H}}}{\bf{C}}({v_1}){\bf{r}} + {{\bf{r}}^{\rm{H}}}{\bf{X}}{({{\bf{X}}^{\rm{H}}}{\bf{X}})^{ - 1}}{{\bf{X}}^{\rm{H}}}{\bf{r}}$ | (11) |
式中,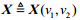 。对目标函数的最优化问题转化为非线性二元目标函数寻优的问题。由于显性的目标函数求导不易实现,本文采用单纯形法求最优值。为提高寻优算法收敛速度,本文对初始值进行了设置。考虑到目标函数项$g({v_1}) \buildrel \Delta \over = {{\bf{r}}^{\rm{H}}}{\bf{C}}({v_1}){\bf{r}}$,即[7]:
。对目标函数的最优化问题转化为非线性二元目标函数寻优的问题。由于显性的目标函数求导不易实现,本文采用单纯形法求最优值。为提高寻优算法收敛速度,本文对初始值进行了设置。考虑到目标函数项$g({v_1}) \buildrel \Delta \over = {{\bf{r}}^{\rm{H}}}{\bf{C}}({v_1}){\bf{r}}$,即[7]:
| $g(v) = - \rho (0) + 2{\mathop{\rm Re}\nolimits} \left[ {\sum\limits_{m = 0}^{N - 1} {\rho (m){{\rm{e}}^{ - {\rm{j}}2{\rm{\pi }}mv}}} } \right]$ | (12) |
式中,$\rho (m) = \sum\limits_{k = m}^{N - 1} {{{[{\bf{A}}{{({{\bf{A}}^{\rm{H}}}{\bf{A}})}^{ - 1}}{{\bf{A}}^{\rm{H}}}]}_{k - m,k}}{\bf{r}}(k){{\bf{r}}^*}(k - m)} $,从而可以通过FFT实现。
3 算法实现流程1) 利用FFT求取式(12)最大值,得到${\hat v_1}$初估计;
2) 对式(11)取绝对值并取对数作为目标函数$f({\bf{x}})$,设置单纯形初始坐标值分别为${x_1} = $ $p[{\hat v_1},{\hat v_1} + 10]$、${x_2} = [{\hat v_1} + 10,{\hat v_1} - 10]$、${x_3} = [{\hat v_1} - 10,{\hat v_1}]$;反射参数$\alpha = 1$,扩展参数$\gamma = 1.5$,收缩参数$\beta = 0.5$,误差界$\varepsilon = 0.001$;
3) 求最大值点${{\bf{x}}_h}$、次大值点${{\bf{x}}_g}$和最小值点${{\bf{x}}_l}$;满足$f({{\bf{x}}_h}) = \max \{ f({{\bf{x}}_i})\} $,$f({{\bf{x}}_g})$= 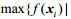
 ,$f({{\bf{x}}_l}) = \min \{ f({{\bf{x}}_i})\} $,$i = 1,2,3$。除${x_h}$外的形心为${\bf{\bar x}} = \frac{1}{3}\left[ {\sum\limits_{i = 1}^3 {{{\bf{x}}_i} - {{\bf{x}}_h}} } \right]$。
,$f({{\bf{x}}_l}) = \min \{ f({{\bf{x}}_i})\} $,$i = 1,2,3$。除${x_h}$外的形心为${\bf{\bar x}} = \frac{1}{3}\left[ {\sum\limits_{i = 1}^3 {{{\bf{x}}_i} - {{\bf{x}}_h}} } \right]$。
4) 反射运算,令${{\bf{x}}_{}} = {\bf{\bar x}} + \alpha ({\bf{\bar x}} - {{\bf{x}}_h})$,计算$f({{\bf{x}}_{}})$。若$f({{\bf{x}}_{}}) < f({{\bf{x}}_l})$,则进行扩展运算,${{\bf{x}}_{}} = {\bf{\bar x}} + \gamma ({{\bf{x}}_{}} - {\bf{\bar x}})$,计算$f({{\bf{x}}_{}})$转到步骤5);若$f({{\bf{x}}_l}) \le f({{\bf{x}}_{}}) \le f({{\bf{x}}_g})$,则${{\bf{x}}_h} = {{\bf{x}}_{}},f({{\bf{x}}_h}) = $ $f({{\bf{x}}_{}})$,转到步骤7);若$f({{\bf{x}}_{}}) > f({{\bf{x}}_g})$,则进行压缩运算,令$f({\bf{x}}) = \min \{ f({{\bf{x}}_h}),f({{\bf{x}}_{}})\} $,${{\bf{x}}_{}} = {\bf{\bar x}} + \beta ({{\bf{x}}_{h'}} - {\bf{\bar x}})$,计算$f({{\bf{x}}_{}})$,转到步骤6);
5) 若$f({{\bf{x}}_{}}) < f({{\bf{x}}_{}})$则${{\bf{x}}_h} = {{\bf{x}}_{}}$,$f({{\bf{x}}_h}) = $ $f({{\bf{x}}_{}})$,转到步骤7);否则:${{\bf{x}}_h} = {{\bf{x}}_{}}$,${{\bf{x}}_h} = {{\bf{x}}_{}}$, $f({{\bf{x}}_h}) = f({{\bf{x}}_{}})$,转到步骤7);
6) 若$f({{\bf{x}}_{}}) \le f({{\bf{x}}_{h'}})$,则${{\bf{x}}_h} = {{\bf{x}}_{}}$,$f({{\bf{x}}_h}) = $ $f({{\bf{x}}_h}) = f({{\bf{x}}_{}})$,转到步骤7);否则进一步收缩运算,${{\bf{x}}_i} = {{\bf{x}}_i} + 0.5({{\bf{x}}_l} - {{\bf{x}}_i}),i = 1,2,3$,$f({{\bf{x}}_i})$转到步骤7);
7)收敛性判断,若满足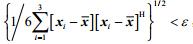 ,则停止;否则转到步骤3)再次寻优;
,则停止;否则转到步骤3)再次寻优;
8) 将估计值${\hat v_1}$、${\hat v_2}$代入式(7)和式(10),令${v_1} = {\hat v_1}$、${v_2} = {\hat v_2}$,求得估计值${{\bf{\hat h}}_1}$、${{\bf{\hat h}}_2}$;
9) 利用估计值${{\bf{\hat h}}_1}$和${{\bf{\hat h}}_2}$,求得相偏估计值${\hat \theta _1}$、${\hat \theta _2}$及幅度估计值${\hat \alpha _1}$、${\hat \alpha _2}$,通过与向量$g(t)$相关处理,求得定时估计值${\hat \tau _1}$、${\hat \tau _2}$。
4 性能分析联合最大似然估计条件下,频偏${v_1}$、${v_2}$估计均方误差CRB推导如下:
令向量${\bf{\Psi }} = ({v_1},{v_2},{h_{1,R}},{h_{1,I}},{h_{2,R}},{h_{2,I}})$,按照CRB定义式[10],有:
| ${[{\bf{F}}]_{i,j}} = - E\left\{ {\frac{{{\partial ^2}\ln \left( {\Lambda ({\bf{r}}\left| {\bf{\Psi }} \right.)} \right)}}{{\partial {\bf{\Psi }}(i)\partial {\bf{\Psi }}(j)}}} \right\}{\rm{ }}0 \le i,j \le 2L + 1$ | (13) |
| ${\mathop{\rm var}} \{ {\hat v_1}\} \ge {[{{\bf{F}}^{ - 1}}]_{11}}$ ${\mathop{\rm var}} \{ {\hat v_2}\} \ge {[{{\bf{F}}^{ - 1}}]_{22}}$ | (14) |
利用式(13)对式(5)各分量分别求二阶偏导,有:
| ${\bf{F}} = \frac{2}{{\sigma _n^2}}\left[ {\begin{array}{*{20}{c}} {\bf{D}}&{{{\bf{U}}^{\rm{H}}}}\\ {\bf{U}}&{\bf{R}} \end{array}} \right]$ | (15) |
式中,
${{\bf{y}}_1} = 2{\rm{\pi diag}}(0,1, \cdots ,N - 1){\bf{A}}{{\bf{h}}_1}$
${{\bf{y}}_2} = 2{\rm{\pi diag}}(0,1, \cdots ,N - 1){\bf{B}}{{\bf{h}}_2}$
${\bf{D}} = \left[ {\begin{array}{*{20}{c}} {{\bf{y}}_1^{\rm{H}}{{\bf{y}}_1}}&{{\mathop{\rm Re}\nolimits} ({\bf{y}}_1^{\rm{H}}{{\bf{\Gamma }}^{\rm{H}}}({v_1}){\bf{\Gamma }}({v_2}){{\bf{y}}_{\rm{2}}})}\\ {{\mathop{\rm Re}\nolimits} ({\bf{y}}_2^{\rm{H}}{{\bf{\Gamma }}^{\rm{H}}}({v_2}){\bf{\Gamma }}({v_1}){{\bf{y}}_1})}&{{\bf{y}}_2^{\rm{H}}{{\bf{y}}_2}} \end{array}} \right]$
${\bf{U}} = \left[ {\begin{array}{*{20}{c}} { - {\mathop{\rm Im}\nolimits} ({{\bf{A}}^{\rm{H}}}{{\bf{y}}_1})}\\ \begin{array}{c} {\mathop{\rm Re}\nolimits} ({{\bf{A}}^{\rm{H}}}{{\bf{y}}_1})\\ - {\mathop{\rm Im}\nolimits} ({{\bf{B}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({{\bf{v}}_2}){{\bf{\Gamma }}^{\rm{H}}}({{\bf{v}}_1}){{\bf{y}}_1})\\ {\mathop{\rm Re}\nolimits} ({{\bf{B}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({{\bf{v}}_2}){{\bf{\Gamma }}^{\rm{H}}}({{\bf{v}}_1}){{\bf{y}}_1}) \end{array} \end{array}{\rm{ }}\begin{array}{*{20}{c}} { - {\mathop{\rm Im}\nolimits} ({{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({{\bf{v}}_{\rm{1}}}){{\bf{\Gamma }}^{\rm{H}}}({{\bf{v}}_{\rm{2}}}){{\bf{y}}_{\rm{2}}})}\\ \begin{array}{c} {\mathop{\rm Re}\nolimits} ({{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({{\bf{v}}_{\rm{1}}}){{\bf{\Gamma }}^{\rm{H}}}({{\bf{v}}_{\rm{2}}}){{\bf{y}}_{\rm{2}}})\\ - {\mathop{\rm Im}\nolimits} ({{\bf{B}}^{\rm{H}}}{{\bf{y}}_2})\\ {\mathop{\rm Re}\nolimits} ({{\bf{B}}^{\rm{H}}}{{\bf{y}}_2}) \end{array} \end{array}} \right]$
| ${\bf{R}} = \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm Re}\nolimits} ({{\bf{A}}^{\rm{H}}}{\bf{A}})}\\ {{\mathop{\rm Im}\nolimits} ({{\bf{A}}^{\rm{H}}}{\bf{A}})}\\ {{\mathop{\rm Re}\nolimits} ({{\bf{B}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_2}){\bf{\Gamma }}({v_1}){\bf{A}})}\\ {{\mathop{\rm Im}\nolimits} (({{\bf{B}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_2}){\bf{\Gamma }}({v_1}){\bf{A}}))} \end{array}{\rm{ }}\begin{array}{*{20}{c}} { - {\mathop{\rm Im}\nolimits} ({{\bf{A}}^{\rm{H}}}{\bf{A}})}\\ {{\mathop{\rm Re}\nolimits} ({{\bf{A}}^{\rm{H}}}{\bf{A}})}\\ { - {\mathop{\rm Im}\nolimits} ({{\bf{B}}^H}{{\bf{\Gamma }}^H}({v_2}){\bf{\Gamma }}({v_1}){\bf{A}})}\\ {{\mathop{\rm Re}\nolimits} ({{\bf{B}}^H}{{\bf{\Gamma }}^H}({v_2}){\bf{\Gamma }}({v_1}){\bf{A}})} \end{array}{\rm{ }}\begin{array}{*{20}{c}} {{\mathop{\rm Re}\nolimits} ({{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_1}){\bf{\Gamma }}({v_2}){\bf{B}})}\\ {{\mathop{\rm Im}\nolimits} ({{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_1}){\bf{\Gamma }}({v_2}){\bf{B}})}\\ {{\mathop{\rm Re}\nolimits} ({{\bf{B}}^{\rm{H}}}{\bf{B}})}\\ {{\mathop{\rm Im}\nolimits} ({{\bf{B}}^{\rm{H}}}{\bf{B}})} \end{array}{\rm{ }}\begin{array}{*{20}{c}} { - {\mathop{\rm Im}\nolimits} ({{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_1}){\bf{\Gamma }}({v_2}){\bf{B}})}\\ {{\mathop{\rm Re}\nolimits} ({{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_1}){\bf{\Gamma }}({v_2}){\bf{B}})}\\ { - {\mathop{\rm Im}\nolimits} ({{\bf{B}}^{\rm{H}}}{\bf{B}})}\\ {{\mathop{\rm Re}\nolimits} ({{\bf{B}}^{\rm{H}}}{\bf{B}})} \end{array}} \right]$ |
利用分块矩阵求逆公式,当${\bf{D}}$、${\bf{R}}$均可逆时,式(15)的逆矩阵可表示为[11]:
| ${{\bf{F}}^{ - 1}} = \frac{{{\sigma _n}^2}}{2}$ $\left[ {\begin{array}{*{20}{c}} {{{({\bf{D}} - {{\bf{U}}^{\rm{H}}}{{\bf{R}}^{ - 1}}{\bf{U}})}^{ - 1}}}&{ - {{\bf{D}}^{ - 1}}{{\bf{U}}^{\rm{H}}}{{({\bf{R}} - {\bf{U}}{{\bf{D}}^{ - 1}}{{\bf{U}}^{\rm{H}}})}^{ - 1}}}\\ { - {{\bf{R}}^{ - 1}}{\bf{U}}{{({\bf{D}} - {{\bf{U}}^{\rm{H}}}{{\bf{R}}^{ - 1}}{\bf{U}})}^{ - 1}}}&{{{({\bf{R}} - {\bf{U}}{{\bf{D}}^{ - 1}}{{\bf{U}}^{\rm{H}}})}^{ - 1}}} \end{array}} \right]$ | (16) |
式中,为求 ${[{{\bf{F}}^{ - 1}}]_{11}}$及${[{{\bf{F}}^{ - 1}}]_{22}}$表达式,需先求${{\bf{R}}^{ - 1}}$。
${{\bf{R}}^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{\mathop{\rm Re}\nolimits} ({\bf{Q}})}\\ {{\mathop{\rm Im}\nolimits} ({\bf{Q}})}\\ { - {\mathop{\rm Re}\nolimits} ({{({{\bf{B}}^{\rm{H}}}{\bf{B}})}^{ - 1}}{{\bf{B}}^{\rm{H}}}{{\bf{Z}}^{\rm{H}}}{\bf{AQ}})}\\ { - {\mathop{\rm Im}\nolimits} (({{({{\bf{B}}^{\rm{H}}}{\bf{B}})}^{ - 1}}{{\bf{B}}^{\rm{H}}}{{\bf{Z}}^{\rm{H}}}{\bf{AQ}}))} \end{array}{\rm{ }}\begin{array}{*{20}{c}} { - {\mathop{\rm Im}\nolimits} ({\bf{Q}})}\\ {{\mathop{\rm Re}\nolimits} ({\bf{Q}})}\\ {{\mathop{\rm Im}\nolimits} ({{({{\bf{B}}^H}{\bf{B}})}^{ - 1}}{{\bf{B}}^H}{{\bf{Z}}^H}{\bf{AQ}})}\\ { - {\mathop{\rm Re}\nolimits} ({{({{\bf{B}}^{\rm{H}}}{\bf{B}})}^{ - 1}}{{\bf{B}}^{\rm{H}}}{{\bf{Z}}^{\rm{H}}}{\bf{AQ}})} \end{array}{\rm{ }}\begin{array}{*{20}{c}} { - {\mathop{\rm Re}\nolimits} ({{\left( {{{\bf{A}}^{\rm{H}}}{\bf{A}}} \right)}^{ - 1}}{{\bf{A}}^{\rm{H}}}{\bf{ZBP}})}\\ { - {\mathop{\rm Im}\nolimits} ({{({{\bf{A}}^{\rm{H}}}{\bf{A}})}^{ - 1}}{{\bf{A}}^{\rm{H}}}{\bf{ZBP}})}\\ {{\mathop{\rm Re}\nolimits} ({\bf{P}})}\\ {{\mathop{\rm Im}\nolimits} ({\bf{P}})} \end{array}{\rm{ }}\begin{array}{*{20}{c}} {{\mathop{\rm Im}\nolimits} ({{({{\bf{A}}^{\rm{H}}}{\bf{A}})}^{ - 1}}{{\bf{A}}^{\rm{H}}}{\bf{ZBP}})}\\ { - {\mathop{\rm Re}\nolimits} ({{({{\bf{A}}^{\rm{H}}}{\bf{A}})}^{ - 1}}{{\bf{A}}^{\rm{H}}}{\bf{ZBP}})}\\ { - {\mathop{\rm Im}\nolimits} ({\bf{P}})}\\ {{\mathop{\rm Re}\nolimits} ({\bf{P}})} \end{array}} \right]$
其中,
$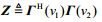 $
$
$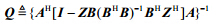 $
$ $
$
将${{\bf{R}}^{ - 1}}$代入式(16),可得:
| ${\mathop{\rm var}} \{ {\hat v_1}\} \ge {[{{\bf{F}}^{ - 1}}]_{11}} = \frac{{{\sigma _n}^2}}{2}\frac{{{\lambda _2}}}{{{\eta _1}{\lambda _2} - {\eta _2}{\lambda _1}}}$ | (17) |
| ${\mathop{\rm var}} \{ {\hat v_2}\} \ge {[{{\bf{F}}^{ - 1}}]_{22}} = \frac{{{\sigma _n}^2}}{2}\frac{{{\eta _1}}}{{{\eta _1}{\lambda _2} - {\eta _2}{\lambda _1}}}$ | (18) |
其中,
$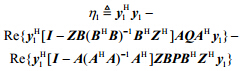 $
$
$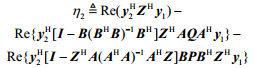 $
$
$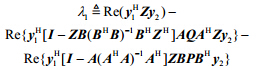 $
$
$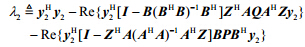 $。
$。
${{\bf{h}}_1}$、${{\bf{h}}_2}$估计均值及方差推导如下,将${\bf{C}}(v)$定义式代入式(10)有:
| $\begin{array}{l} {\rm{ }}{{{\bf{\hat h}}}_2} = {[{\bf{X}}{({{\hat v}_1},{{\hat v}_2})^{\rm{H}}}{\bf{X}}({{\hat v}_1},{{\hat v}_2})]^{ - 1}}{\bf{X}}{({{\hat v}_1},{{\hat v}_2})^{\rm{H}}}{\bf{r}} = \\ \quad {[{\bf{X}}{({{\hat v}_1},{{\hat v}_2})^{\rm{H}}}{\bf{X}}({{\hat v}_1},{{\hat v}_2})]^{ - 1}}{\bf{X}}{({{\hat v}_1},{{\hat v}_2})^{\rm{H}}}[{\bf{I}} - {\bf{C}}({{\hat v}_1})] \times \\ \quad \;\;{\rm{ }}\;{\rm{ }}[{\bf{\Gamma }}({v_1}){\bf{A}}{{\bf{h}}_1} + {\bf{\Gamma }}({v_2}){\bf{B}}{{\bf{h}}_2} + {\bf{w}}] \end{array}$ | (19) |
| ${\hat h_1} = {({A^{\rm{H}}}A)^{ - 1}}{A^{\rm{H}}}{\Gamma ^{\rm{H}}}({\hat v_1})[r - \Gamma ({\hat v_2})B{\hat h_2}]$ | (20) |
由$[{\bf{I}} - {\bf{C}}({v_1})]{\bf{\Gamma }}({v_1}){\bf{A}}{{\bf{h}}_1} = 0$,$E({\hat v_1}) = {v_1}$, $E({\hat v_2})$ = ${v_2}$,有:
$E({{\bf{\hat h}}_2}) = {{\bf{h}}_2}$
$E({{\bf{\hat h}}_1}) = {{\bf{h}}_1}$
$E(||{{\bf{\hat h}}_2} - {{\bf{h}}_2}|{|^2}) = \frac{{\sigma _n^2}}{2}{\rm{tr\{ [}}{\bf{X}}{({v_1},{v_2})^{\rm{H}}}{\bf{X}}({v_1},{v_2}){{\rm{]}}^{ - 1}}{\rm{\} }}$
$E(||{{\bf{\hat h}}_1} - {{\bf{h}}_1}|{|^2}) = \frac{{\sigma _n^2}}{2}{\rm{tr((}}{{\bf{A}}^{\rm{H}}}{\bf{A}}{{\rm{)}}^{ - 1}}{\rm{)}} + \frac{{\sigma _n^2}}{2} \times $
${\rm{tr}}\left( \begin{array}{l} {{\rm{(}}{{\bf{A}}^{\rm{H}}}{\bf{A}}{\rm{)}}^{ - 1}}{{\bf{A}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_1}){\bf{\Gamma }}({v_2}){\bf{B}}{({\bf{X}}{({v_1},{v_2})^{\rm{H}}}{\bf{X}}({v_1},{v_2}))^{ - 1}} \times \\ {{\bf{B}}^{\rm{H}}}{{\bf{\Gamma }}^{\rm{H}}}({v_2}){\bf{\Gamma }}({v_1}){\bf{A}}{({{\bf{A}}^{\rm{H}}}{\bf{A}})^{ - 1}} \end{array} \right)$
由式(17)和式(18)可知,混合信号条件下频偏估计CRB与信噪比Es/N0、信号功率比SINR、两信号频偏差有关。取Es/N0=16 dB,两信号频偏差为0,频偏估计CRB随SINR变化关系如图 1所示,其中单信号模型下频偏估计CRB见文献[7]。
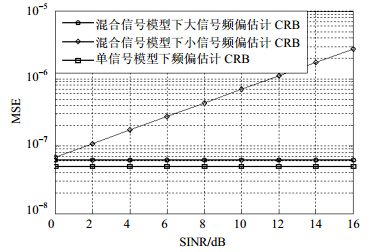 |
| 图 1 频偏估计CRB随信号功率比变化图 |
取SINR=8 dB,Es/N0=16,频偏估计CRB随两信号频偏差变化关系如图 2所示。
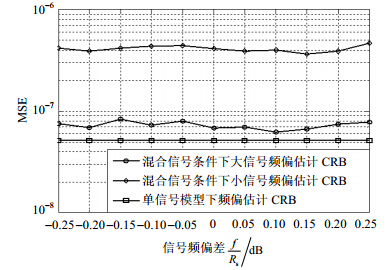 |
| 图 2 频偏估计CRB随信号频率差变化图 |
由图 1知,在两信号功率相当时,频偏估计CRB相同,随着SINR增大,小信号估计均方误差增大。混合信号条件下大信号频偏估计CRB大于同功率单信号的值。由图 2知,混合信号条件下频偏估计CRB受频偏差影响不明显。
5 仿真分析仿真条件:两路信号均为QPSK调制,数字下变频后3倍采样,帧头数据长度均为64符号,进行500次Monte-Carlo试验。
仿真一:大信号功率远大于小信号,定时误差为1/3T,本文算法与经典算法频偏估计均方误差随大信号信噪比变化关系如图 3所示。
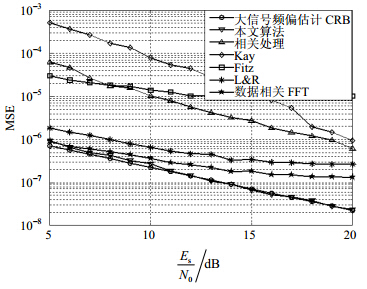 |
| 图 3 频偏估计均方误差随信噪比变化图(定时偏差1/3T) |
仿真二:大信号信噪比为16 dB,两信号功率比SINR在0~16 dB变化时,无定时误差,本文算法与经典算法频偏估计均方误差随功率比变化关系如图 4所示。其中,仿真条件①指符号长度为64,仿真条件②指符号长度为128;一路信号全部符号信息已知,另一路信号仅帧头已知,未知符号设置为全零。
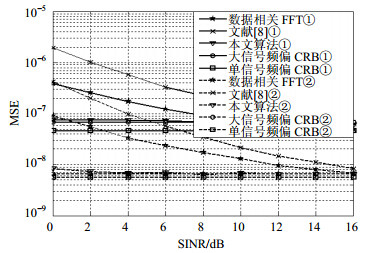 |
| 图 4 频偏估计均方误差随功率比变化图(无定时误差) |
仿真三:仿真条件如仿真二,本文算法信道估计均方误差随SINR变化如图 5所示。
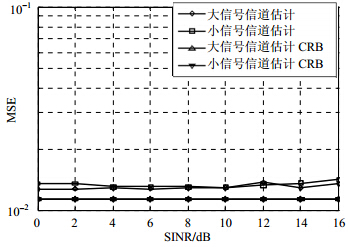 |
| 图 5 信道估计均方误差随信号功率比变化图 |
仿真四:两信号功率比SINR为8 dB,大信号信噪比0~16 dB变化时,本文算法信道估计均方误差随信噪比变化如图 6所示。
 |
| 图 6 信道估计均方误差随信噪比变化图 |
由仿真一可知,本文算法在大信号功率远大于小信号时,对大信号频偏估计性能优良,不受信道特性影响。由仿真二可知,本文算法对大信号频偏估计精度不受信号功率比SINR及信道特性影响,性能逼近混合信号频偏估计CRB。在利用一路信号全部符号信息条件下,通过对另一路信号未知符号填零,本文算法能具有更优良的性能。由仿真三四可知,本文算法信道估计精度逼近CRB且估计精度不受SINR影响。
6 计算量分析本文算法最大的运算量消耗在频率联合估计式(11)目标函数寻优中。考虑到${\bf{A}}{({{\bf{A}}^{\rm{H}}}{\bf{A}})^{ - 1}}{{\bf{A}}^{\rm{H}}}$、${\bf{B}}{({{\bf{B}}^{\rm{H}}}{\bf{B}})^{ - 1}}{{\bf{B}}^{\rm{H}}}$均可预先计算直接调用即可。${\bf{C}}({v_1})$求取需$2{N^2}$次复乘,${\bf{X}}({v_1},{v_2})$求取需$(L + 1){N^2}$次复乘,$N + (N - 1)NL$次复加,${\bf{X}}{({v_1},{v_2})^{\rm{H}}}{\bf{X}}({v_1},{v_2})$需$N{L^2}$次复乘,$(N - 1){L^2}$次复加,${[{\bf{X}}{({v_1},{v_2})^{\rm{H}}}{\bf{X}}({v_1},{v_2})]^{ - 1}}$为Hermite矩阵,考虑到分块矩阵求逆性质[12]需${L^3}$次复乘及${L^3}$次复加。一次复乘需要4次实乘及2次实加,一次复加需要2次实加,则式(11)共需$O({N^2}L)$次乘法及$O({N^2}L)$次加法运算。
7 结 束 语本文针对PCMA混合信号模型,构建了混合信号条件下最大似然目标函数,推导了混合信号频偏、相偏、信道联合估计表达式。算法估计性能逼近混合信号模型CRB下界。
| [1] | DANKBERG M D, MILLER M J, MULLIGAN M G. Self-interference cancellation for two-party relayed communication: US, 5596439[P]. 1997-1-21. |
| [2] | 廖灿辉. 卫星同频混合信号的单通道接收处理与应用技术研究[D]. 北京: 清华大学, 2010. LIAO Can-hui. Single-channel processing technology on satellite co-frequency signals and its application[D]. Beijing: TsingHua University, 2010. |
| [3] | OERDER M, MEYR H. Digital filter and square timing recovery[J]. IEEE Trans on Commun, 1988, 36: 605-612. |
| [4] | KAY S M. A fast and accurate single frequency estimator[J]. IEEE Trans on Acoustic, Speech, and Signal Processing, 1989, 37 (12):1987-1989. |
| [5] | FITZ M P. Planar filtered techniques for burst mode carrier synchronization[C]//IEEE GLOBECOM'91. Phoenix, AZ, USA: IEEE Press, 1991. |
| [6] | LUISE M, REGGIANNINI R. Carrier frequency recovery in all-digital modems for burst-mode transmissions[J]. IEEE Trans on Commun, 1995, 43(3): 1169-1178. |
| [7] | MORELLI M, MENGALI U. Carrier-frequency estimation for transmissions over selective channels[J]. IEEE Trans on Commun, 2000, 48(9): 1580-1589. |
| [8] | 万坚, 李明, 朱中梁. 一种新型卫星多址方式的分离新算法[J]. 系统仿真学报, 2006, 18(7): 1799-1801. WAN Jian, LI Ming, ZHU Zhong-liang. A novel separation algorithm of a new multiple access mode in satellite[J]. Journal of System Simulation, 2006, 18(7): 1799-1801. |
| [9] | 廖灿辉, 周世东, 朱中梁. 基于最大似然的同频混合信号联合定时估计算法[J]. 系统工程与电子技术,2010, 32(6): 1121-1124. LIAO Can-hui, ZHOU Shi-dong, ZHU Zhong-liang. ML- based joint timing estimation algorithm for co-frequency signals[J]. Systems Engineering and Electronics, 2010, 32(6): 1121-1124. |
| [10] | KAY S M. Fundamental of statistical signal processing[M]. Englewood Cliffs, NJ, USA: Prentice-Hall, 1993. |
| [11] | KAILATH T, SAYED A H, HASSIBI B. Linear estimation[M]. Englewood Cliffs, NJ, USA: Prentice-Hall, 2000. |
| [12] | 高飞, 王永良, 陈辉, 等. STAP中的矩阵求逆问题研究[J]. 雷达科学与技术, 2008, 6(3): 215-218. GAO Fei, WANG Yong-liang, CHEN Hui, et al. Study on matrix inversion for STAP[J]. Radar Science and Techno1ogy, 2008, 6(3): 215-218. |
 2015, Vol. 44
2015, Vol. 44
