研究表明,60%的语音业务和近90%的数据业务发生在室内[1]。而支持短距离、低功率通信的femtocell作为新一代无线通信技术特别适用于宏蜂窝网络覆盖不足或用户量骤增的室内环境。femtocell数量众多,引起的能量消耗不容忽视,因此在femtocell网络设计中,采用绿色节能的通信技术是必然趋势。
文献[2]提出能量效率概念(单位:bit/J),表示单位能量所能正确传输的数据速率。当前研究femtocell网络中基于能量效率的资源分配算法大都复杂度较高,或者只能针对单个小区的情况,而没有考虑相邻小区的同频干扰。文献[3]提出了一种基于非合作博弈理论优化网络能量效率的功率控制算法,但该算法复杂度过高。文献[4]提出了一种低复杂度的节能功率分配方案,但该方法没有考虑到相邻小区的干扰。文献[5]提出了一种基于Stackelberg博弈的高能量效率资源分配方法,得到了功率最优响应的闭式解,但该方法没有引入干扰抑制机制,使得家庭基站对宏基站干扰过大。文献[6]提出了一种低复杂度的高能效的功率分配算法,但采用的是单一定价机制,并没考虑信道差异。
本文研究了femtocell双层网络上行链路中基于节能的功率控制问题。采用Stackelberg博弈(Stackelberg game,SG)模型,引入动态定价保护机制,对家庭用户(femtocelluser equipment, FUE)的发射功率进行限制,从而对宏基站进行干扰保护,同时最大化家庭用户的能量效率。本文首先给出femtocell双层网络功率控制模型;然后给出基于Stackelberg博弈的资源分配模型以及该博弈模型下Stackelberg均衡解存在性与唯一性的证明;再通过引入指数级低通滤波器(exponentially weighted moving average,EWMA)的思想,得到宏基站干扰价格与家庭用户发射功率最优响应的闭式解;最后提出一种基于Stackelberg博弈的高能量效率功率控制算法(Stackelberg game based energy-efficient power control algorithm,SEPCA)。仿真结果表明,与算法NPCA相比,SEPCA算法在付出较低的能量效率降低的代价下,极大地减小了计算复杂度。 1 femtocell双层网络功率控制模型 1.1 能量效率模型
本文研究了由单个宏基站和多个家庭基站组成的femtocell双层网络中上行链路的功率分配问题。场景图如图 1所示,图中MUE表示宏用户(macrocell user equipment,MUE)。为研究方便,假设家庭基站给家庭用户分配单个子信道,且每个子信道只分配给一个用户。$I = [{C_1},{C_2}, \cdots ,{C_I}]$表示占用相同子信道的家庭用户集合;$F = [{F_1},{F_2}, \cdots ,{F_I}]$表示家庭基站集合;$F = [{F_1},{F_2}, \cdots ,{F_I}]$表示家庭用户${C_i}$到为其服务的家庭基站${F_i}$的功率增益;${h_{i,j}}$和${g_{0,i}}$分别表示${C_i}$到其邻近的${F_i}$及宏基站${M_0}$的干扰增益。此外,考虑到家庭用户活动范围有限,认定所有信道在时隙内的信道增益保持不变。假设信道状态信息可由移动终端无差错无延时反馈到基站,则${C_i}$的信干噪比为:
| ${\gamma _i} = {p_i}{h_{i,i}}/(\sum\limits_{j \ne i} {{p_j}{h_{i,j}}} + \sigma _i^2)$ | (1) |
式中,${p_i}$为${C_i}$的发射功率;$\sigma _i^2$为加性高斯白噪声功率。根据香农容量公式,家庭基站${F_i}$中的${C_i}$可获得的最大比特速率为:
| ${r_i} = {B_i}{\log _2}(1 + {\gamma _i})$ | (2) |
把能量效率表示为瞬时传输速率和瞬时功率之比,则${C_i}$瞬时能量效率的表达式为:
| $ {e_i} = \frac{{{B_i}{{\log }_2}(1 + {\gamma _i})}}{{{p_i} + {p_c}}}$ | (3) |
式中,${B_i}$为家庭用户单个子信道的传输带宽;${p_c}$表示电路消耗功率,包括除功率放大器外其他电子设备的平均能耗,一般为常数。
 |
| 图 1 femtocell双层网络模型 |
本文宏基站采用动态定价的方式控制家庭用户的发射功率,以最大化家庭用户的干扰收益。家庭用户根据宏基站的定价,选择相应的发射功率以最大化净收益。令宏基站对家庭用户${C_i}$的单位干扰定价为${w_i}$,则${C_i}$的优化目标为:
| $\begin{array}{l} {P_1}:{\rm{ }}\max {e_i}({p_i},{p_ - }_i) - {w_i}{g_{0,i}}{p_i}\\ {\rm{ s}}{\rm{.t}}{\rm{. }}0 \le {p_i} \le p_i^{\max } \end{array}$ | (4) |
即最大化家庭用户${C_i}$瞬时能效值与对宏基站造成的干扰所付出的“代价”之差。式中,${p_{ - i}}$表示除了家庭用户${C_i}$以外其他家庭用户的功率集合;$p_i^{\max }$为${C_i}$的最大允许发射功率。
宏基站制定最优干扰价格${\bf{w}}$以最大化自身干扰收益。宏基站的优化目标可表述为[8]:
| $% {P_2}:{\rm{ }}\max \sum\limits_{i = 1}^I {{w_i}I'({p_i})} $ | (5) |
式中,$I'({p_i}) = {g_{0,i}}{p_i},\forall i \in I$,表示家庭用户${C_i}$对宏用户产生的干扰,$w = [{w_1},{w_2}, \cdots ,{w_i}, \cdots ,{w_I}]$为宏基站对家庭用户的干扰定价矢量。
本文采用的主要数学符号定义如下:${\bf{w}}$表示宏基站的干扰定价;$\lambda $表示EWMA的平滑因子;${f_h}$、${f_m}$分别表示家庭用户与宏基站效用函数;$T(t)$、$P(t)$分别表示家庭用户基于时间平均的速率值以及发射功率与${p_c}$的总和。 2 基于SG的分布式功率分配策略 2.1 Stackelberg博弈建模
本小节将上述宏基站与家庭用户的优化问题${P_1}$与${P_2}$转化为Stackelberg博弈问题。Stackelberg博弈是一种纯策略的非合作博弈。在Stackelberg博弈中,根据行动的优先级以及掌握信息的完整程度,博弈的参与者可以分为领导者和跟随者[5]。跟随者只掌握部分信息,率先行动。而领导者由于掌握跟随者全部信息,随后行动。在本文中,由于宏基站掌握全局信息,让宏基站充当领导者,家庭用户充当跟随者。首先家庭用户根据干扰价格更新最优的发射功率;然后宏基站根据家庭基站的功率策略进行定价;最后达到SG均衡(Stackelberg game equipment,SE)。
定义1 策略组合$({w^{{\rm{SE}}}},{{\bf{p}}^{{\rm{SE}}}})$为SE解,当且仅当满足下述条件[5]:
| $f({w^{{\rm{SE}}}},{p^{{\rm{SE}}}}) \ge f(w,p)$ | (6) |
这样的博弈模型下,此femtocell双层网络的优化分成两层优化完成,其中宏基站侧的效用函数为:
| ${f_m}(w,p) = \sum\limits_{i = 1}^I {{w_i}{{I'}_i}({p_i}){\rm{ }}} {I'_i}({p_i}) = {g_{0,i}}{p_i}$ | (7) |
家庭用户侧SG中,基于定价的非合作子博弈可表示为$G = \{I ,{\{ {p_i}\} _{i \in I}},{\{ {f_h}({p_i},{p_{ - i}},{w_i})\} _{i \in I}}\} $。其中,${\bf{I}}$表示参与博弈的家庭用户集合;${p_i} \in [0,P_i^{\max }]$表示家庭用户${p_i} \in [0,P_i^{\max }]$采取的功率策略;${f_h}({p_i},{p_{ - i}},{w_i})$表示家庭用户${C_i}$的效用函数:
| $ {f_h}({p_i},{p_{ - i}},{w_i}) = {e_i}({p_i}) - {w_i}{g_{0,i}}{p_i}$ | (8) |
家庭用户侧进行非合作博弈的最终目的是找到最优发射功率,并通过用户间的多次博弈,达到纳什均衡状态。
定义2 给定${p_{ - i}}(t)$以及干扰价格矢量$w(t)$时,满足$p_i^*(t){\rm{ = }}\arg \max {f_h}[{p_i}(t),{p_{ - i}}(t),w(t)]$的功率策略,$p_i^*(t)$称为功率最优响应策略。
定义3 对任意给定的用户${C_i},i \in I$,给定${p_{ - i}}(t)$及干扰价格矢量$w(t)$时,都有${f_h}[{p_i}^{{\rm{SE}}}(t),{p_{ - i}}(t),w(t)] \ge {f_h}[{p_i}(t),{p_{ - i}}(t),w(t)]$成立,则功率矢量${p^{{\rm{SE}}}}(t) = [p_{\rm{1}}^{{\rm{SE}}}(t),p_{\rm{2}}^{{\rm{SE}}}(t), \cdots ,p_I^{{\rm{SE}}}(t)]$被称为${\bf{G}}$的纳什均衡解[8]。
可以看出,纳什均衡解是指所有参与者不能通过单独改变策略而使其收益有所增加的策略组合,是任何参与者都不愿背离的平衡状态。 2.2 基于EWMA的功率优化策略
文献[7]表明,在给定${p_{ - i}}$和${w_i}$时,式(8)为非凸函数,因此无法使用凸优化方法获得最佳发射功率的闭式解,从而造成式(8)优化的复杂度过高。鉴于此,本文引入EWMA来获得最佳发射功率的闭式解,降低运算复杂度。
EWMA也叫指数平滑法[8],即利用过去观察值预测当前值的数学方法,预测模型为:
| $ {G'_{t + 1}} = \alpha {G_t} + (1 - \alpha ){G'_t}$ |
式中,${G'_{t + 1}}$为$t + 1$期的预测值;${G_t}$为$t$期的观察值,${G'_t}$为$t$期的预测值;$\alpha (0 \le \alpha \le 1)$为平滑因子。换句话说,一旦选定平滑因子,任一期的平滑值都是本期观察值与前一期平滑值的加权平均。
根据EWMA的思想,家庭用户${C_i}$在$t$时隙基于时间平均的数据速率[4]为:
| ${T_i}(t) = (1 - \lambda ){T_i}(t - 1) + \lambda {r_i}(t){\rm{ }}0 < \lambda < < 1$ | (9) |
式中,$\lambda $为平滑系数,表示预测值精度。$\lambda $越大,预测值误差越小。${T_i}(t - 1)$表示家庭用户${C_i}$在$t - 1$时隙的传输速率,对$t$时隙来说,相当于常量。
相似地,${C_i}$在$t$时隙功率的平滑值为:
| ${P_i}(t) = (1 - \lambda ){P_i}(t - 1) + \lambda ({p_i}(t) + {p_c})$ | (10) |
式中,${P_i}(t)$为家庭用户${C_i}$在$t$时隙的发射功率与${p_c}$之和。根据式(9)和式(10),家庭用户${C_i}$基于EWMA的能量效率模型式(8)[4]可转化为:
| ${f_h}(t) = \frac{{(1 - \lambda ){T_i}(t - 1) + \lambda {r_i}(t)}}{{(1 - \lambda ){P_i}(t - 1) + \lambda ({p_i}(t) + {p_c})}} - {w_i}(t){g_{0,i}}{p_i}(t){\rm{ }}$ | (11) |
定理1 ${f_h}[{p_i}(t),{p_{ - i}}(t),{w_i}(t)]$在${p_i}(t)$上具有连续性,而且关于${p_i}(t)$拟凹。
证明 根据文献[10]的命题C.9,${f_h}({p_i}(t))$是严格拟凹的,如果其上轮廓集:
| ${\Gamma _\alpha }({f_h}({p_i}(t),\alpha ) = \{ {p_i}(t) \ge 0|{f_h}({p_i}(t)) \ge \alpha \} $ | (12) |
对于$\forall \alpha \in R$,${\Gamma _\alpha }$是严格凸集:
| $\begin{array}{l} {\Gamma _\alpha }(t) = \left\{ {\left. {{p_i}(t) \ge 0} \right|\frac{{(1 - \lambda ){T_i}(t - 1) + \lambda {r_i}(t)}}{{(1 - \lambda ){P_i}(t - 1) + \lambda {p_i}(t)}} - {w_i}(t){g_{0,i}}{p_i}(t) \ge \alpha } \right\} = \\ \left\{ {\left. {{p_i}(t) \ge 0} \right|\lambda {r_i}(t) - {w_i}(t){g_{0,i}}\lambda {p_i}^2(t) - [{w_i}(t){g_{0,i}}(1 - \lambda ){P_i}(t - 1) + \alpha \lambda ]} \right.{p_i}(t) + {S_i}\left. { \ge 0} \right\} \end{array}$ | (13) |
式中,${S_i} = (1 - \lambda )[{T_i}(t - 1) - \alpha {P_i}(t - 1)]$为常数。
当$\alpha \le 0$时,${f_h}[{p_i}(t),{p_{ - i}}(t),{w_i}(t)] \ge \alpha $,对所有的${p_i}(t)$都成立,于是${\Gamma _\alpha }(t)$是严格凸集;当$\alpha > 0$时,${r_i}(t)$是${p_i}(t)$的对数函数,属于严格凹函数。
式(13)中$ - {w_i}(t){g_{0,i}}\lambda {p_i}^2(t)$为凹函数,$ - {\rm{[}}{w_i}(t){g_{0,i}}(1 - \lambda ){P_i}(t - 1) + \alpha \lambda {\rm{]}}{p_i}(t)$是${p_i}(t)$的线性函数,也是凹函数。根据凸优化理论,有限个凹函数的和也是凹函数,因此${\Gamma _\alpha }(t)$是严格凸集。故有,$\forall \alpha \in R$,${\Gamma _\alpha }(t)$是严格凸集。证毕。
由于${f_h}[{p_i}(t),{p_{ - i}}(t),{w_i}(t)]$关于${p_i}(t)$是严格拟凹的,家庭用户${C_i}$存在唯一的最优发射功率$p_i^*(t)$,则$p_i^*(t)$可通过下式求解:
| $ \partial {f_h}[{p_i}(t),{p_{ - i}}(t),{w_i}(t)]/\partial {p_i}(t) = 0$ | (14) |
对式(11)求一阶微分,可得:
| $ \frac{{\partial {f_h}(t)}}{{\partial {p_i}(t)}} = \left[ {\frac{{\partial {r_i}(t)}}{{\partial {p_i}(t)}}{P_i}(t) - {T_i}(t)\lambda } \right]/P_i^2(t) - {w_i}(t){g_{0,i}}$ | (15) |
设式(13)偏导值为0,得:
| $\frac{{\partial {r_i}(t)}}{{\partial {p_i}(t)}} = \frac{{{w_i}(t){g_{0,i}}}}{\lambda }{P_i}(t) + \frac{{{T_i}(t)}}{{{P_i}(t)}}$ | (16) |
根据指数低通滤波器思想,当$0 < \lambda < < 1$时,${T_i}(t) \approx {T_i}(t - 1),{P_i}(t) \approx {P_i}(t - 1)$成立,则式(14)变为:
| $\begin{array}{l} \frac{{\partial {r_i}(t)}}{{\partial {p_i}(t)}} \approx \frac{{{w_i}(t){g_{0,i}}}}{\lambda }{P_i}(t - 1) + \frac{{{T_i}(t - 1)}}{{{P_i}(t - 1)}} {\rm{ = }}\\ \frac{{{w_i}(t){g_{0,i}}}}{\lambda }{P_i}(t - 1) + {e_i}(t - 1) \end{array}$ | (17) |
根据式(2),${r_i}(t)$是关于${p_i}(t)$的函数,得:
| $\frac{{\partial {r_i}(t)}}{{\partial {p_i}(t)}}{\rm{ = }}\frac{{{B_i}}}{{\ln 2}}\frac{{{h_{i,i}}}}{{{h_{i,i}}{p_i}(t) + \sum\limits_{j \ne i} {{p_j}{h_{i,j}}} + \sigma _i^2}}$ | (18) |
更进一步,联立式(17)和式(18)可得功率最优解为:
| $\begin{array}{c} p_i^{\rm{*}}(t) = \\ \left\{ \begin{array}{l} 0{\rm{ }}{p_i}(t) \le 0\\ \frac{B}{{\ln 2\{ \frac{{{w_i}(t){g_{0,i}}}}{\lambda }{P_i}(t - 1) + {e_i}(t - 1)\} }} - \\ \frac{{\sigma _i^2 + \sum\limits_{j \ne i} {{p_j}{h_{i,j}}} }}{{{h_{i,i}}}}{\rm{ }}0 < {p_i}(t) < p_i^{\max }(t)\\ p_i^{\max }(t){\rm{ }}{p_i}(t) \ge p_i^{\max }(t) \end{array} \right. \end{array}$ | (19) |
在博弈中,家庭基站向宏基站购买功率,宏基站根据家庭基站购买的功率指定干扰价格,于是${w_i}(t)$是$p_i^{\rm{*}}(t)$的函数[7]。将式(19)代入式(7),宏基站的效用函数变为:
| $\max {f_m}(w,p) = \max \sum\limits_{i = 1}^I {\left( {\frac{{{B_i}}}{{\ln 2\left( {\frac{1}{\lambda }{P_i}(t - 1) + \frac{{{e_i}(t - 1)}}{{{g_{0,i}}{w_i}(t)}}} \right)}} - \frac{{(\sigma _i^2 + \sum\limits_{j \ne i} {{p_j}{h_{i,j}}} ){g_{0,i}}{w_i}(t)}}{{{h_{i,i}}}}} \right)} $ | (20) |
${f_m}(w,p)$关于${w_i}(t)$的二阶偏导为:
| $\frac{{{\partial ^2}{f_m}({w_i}(t))}}{{\partial w_i^2(t)}} = - {e_i}^2(t - 1){B_i}/\left( {\frac{1}{\lambda }{e_i}(t - 1){w_i}(t) + \frac{{{e_i}(t - 1)}}{{{g_{0,i}}}}} \right)$ | (21) |
由式(21)可知 ${\partial ^2}{f_m}({w_i}(t))/\partial w_i^2(t) < 0$,可得${f_m}({w_i}(t))$是${w_i}(t)$的严格凹函数,因此宏基站最优定价的必要条件是$\partial {f_m}({w_i}(t))/\partial {w_i}(t) = 0$。
| ${w_i}^{{\rm{SE}}}(t) = \frac{\lambda }{{{g_{0,i}}{P_i}(t - 1)}} \times \left( {\sqrt {\frac{{{B_i}{h_{i,i}}{e_i}(t - 1)}}{{(\sigma _i^2 + \sum\limits_{j \ne i} {{p_j}{h_{i,j}}} )\ln 2}}} - {e_i}(t - 1)} \right)$ | (22) |
定理 2家庭用户侧$G$存在纳什均衡解。
证明 根据纳什定理${f_h}[{p_i}(t),{p_{ - i}}(t),{w_i}(t)]$,如果满足以下两个条件,则存在纳什均衡解:
1)${p_i}(t)$是欧氏空间非空、有界、闭凸集;
2) ${p_i}(t)$在${p_i}(t)$上具有连续性,而且关于${p_i}(t)$拟凹。
家庭用户的功率策略空间定义在$[0,p_i^{\max }(t)]$。显然${f_h}[{p_i}(t),{p_{ - i}}(t),{w_i}(t)]$关于${p_i}(t)$连续,条件1) 满足。由于${f_h}[{p_i}(t),{p_{ - i}}(t),{w_i}(t)]$由简单函数组成,因此它在${p_i}(t)$是连续的。而拟凹性在定理1中给出了证明。于是条件2)满足。证毕。
定理 3家庭用户侧$G$的纳什均衡解唯一。
详情查阅文献[11]。
定理 4此Stackelberg博弈存在唯一均衡解$[{w^{{\rm{SE}}}}(t),{p^{{\rm{SE}}}}(t)]$。
从定理2、定理3和引理1可得此结论。 2.4 分布式算法描述
本文通过提出SEPCA算法使家庭用户与宏基站在各时隙均达到SE状态。具体过程如下:
1) 令时隙$t = 0$。初始化家庭用户发射功率为$p(0)$,能量效率为$e(0)$;家庭用户侧子博弈迭代上限为$M$;
2) 令$t = t + 1$,根据定价因子闭式解式(22)计算定价矢量$w(t)$;
3) 利用步骤2)中的$w(t)$和式(19)计算功率最优反应闭式解${p^*}(t)$;
4) 若家庭用户侧子博弈收敛或迭代次数达到上限$M$,则$t$时隙的该子博弈结束;否则返回步骤3);
5) 利用式(3)计算$e(t)$;
6) 若通信结束,算法结束;否则返回步骤2)。 2.5 复杂度分析
对于传统的瞬时能效函数而言,在求解$p_i^{\rm{*}}(t) = \arg \max {f_h}({p_i}(t))$时,需要设计专门的寻优迭代算法。令$N$表示发射功率区间离散值的个数。采用最经典的二分法寻找最优发射功率,其计算复杂度为$O({\log _2}N)$,文献[3]的NPCA算法复杂度为$O({\log _2}(2N))$,且随博弈迭代次数的增加,计算复杂度将线性增加。本文SEPCA算法的复杂度为$O(1)$,明显比其他算法低。 3 仿真结果
本文的仿真在基于3GPP的宏小区与家庭基站小区共存的双层网络仿真平台上进行,其中双层网络由单宏小区和其内部署的多个femtocell组成。每个家庭基站中有3个家庭用户,其附近随机部署多个宏用户。系统载频为2 GHz,每个用户传输带宽${B_i}$为10 MHz,电路损耗功率${p_c}$为10 mW。信道采用12径瑞利信道,并考虑阴影衰落和快衰落。仿真中假设没有子载波间干扰和符号间串扰,并且家庭基站可以获得本小区内用户的信道状态信息。
文献[3]提出基于超模博弈的NPCA算法,得到了帕累托最优解,但无法求得功率最优响应闭式解,算法复杂度高。本文通过分析不同的平滑因子$\lambda $和家庭基站数量下,家庭用户平均能量效率和平均发射功率,并与NPCA算法进行对比,评估所提SEPCA算法的性能。
图 2为采用SEPCA算法时所有家庭用户的平均发射功率值随迭代次数的变化情况,其中家庭用户数$I = 30$,平滑因子$\lambda = 0.1$。由图可见,在迭代11次以后,功率基本收敛。博弈初期,各家庭用户初始功率较小,在其他家庭用户功率策略不变的情况下,会自私地增加发射功率以增加自身收益。但由于定价保护,在功率达到某个值后,收益不再增加,功率值达到动态平衡。
图 3为所有家庭用户平均能量效率随平滑因子$\lambda $变化的曲线图,其中家庭用户数$I = 30$。由图可见,随着$\lambda $增加,这30个家庭用户的平均能量效率降低。因为SEPCA算法用式(9)与式(10)对家庭用户发射功率和传输速率做近似。$\lambda $越大,家庭用户发射功率和传输速率预测误差越大,信号损失随之增加,系统平均能量效率降低。
图 4给出了家庭用户平均能量效率随家庭基站数量大小变化的曲线,其中平滑因子$\lambda = 0.1$。由图可见,随着家庭基站数量增加,家庭用户平均能量效率下降。对某个家庭用户来说,在发射功率不变时,家庭基站数量增加,则同频干扰源增加,引起家庭用户间的干扰增加,从而导致家庭用户平均能量效率下降。
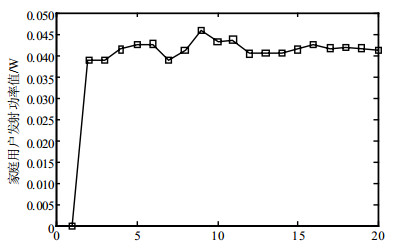 |
| 图 2 家庭用户发射功率收敛曲线 |
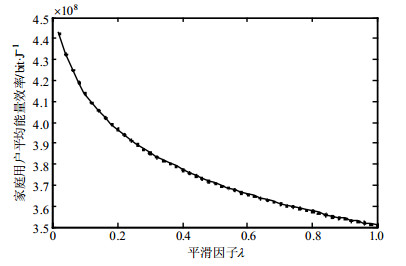 |
| 图 3 家庭用户平均能效与平滑因子的关系 |
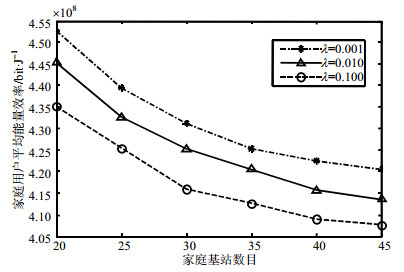 |
| 图 4 用户平均能效与基站数目、平滑因子的关系 |
图 5为NPCA算法和SEPCA算法的能量效率对比图,其中平滑因子$\lambda = 0.1$。由图可见,随着家庭基站数量增加,两种算法中家庭用户平均能量效率都会下降,但是SEPCA算法得到的能量效率比NPCA算法略低。因为SEPCA算法采用EWMA对功率与速率做了近似,会造成部分信息损失,而NPCA算法得到的是功率精确值。因此本文所采用的SEPCA算法能量效率要比NPCA算法略差,是一种次优算法。尽管能量效率有损耗,但是用能量效率性能的较小损失换取算法复杂度的大大降低,也间接达到了节能的目的。
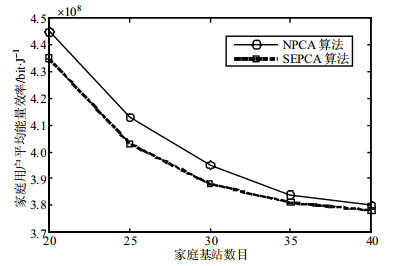 |
| 图 5 SEPCA与NPCA的用户能效对比图 |
图 6表示在NPCA算法和SEPCA算法下,宏基站性能的对比图,其中宏用户数假设为10。由图可知,采用SEPCA算法时,10个宏用户受到的干扰总和降低了约10 dBm。这是由于本方法采用了动态定价机制,减少了FBS的发射功率的缘故。此外,提出的SEPCA由于考虑到各个FBS链路的差异性,采用独立定价方法也能更多地降低对MUE的干扰。
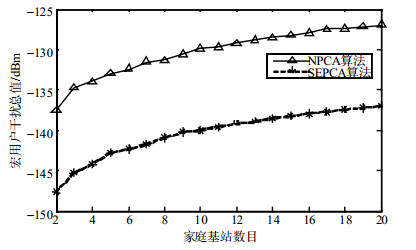 |
| 图 6 不同算法下宏用户干扰值对比图 |
本文提出了femtocell双层网络中基于SG的功率控制算法SEPCA,并证明了SE的存在性与唯一性,给出了定价因子及分布式的功率最优响应闭式解的求解算法。SEPCA算法在求解功率最优响应时复杂度为$O(1)$,明显低于NPCA算法。SEPCA算法充分考虑到各个FBS链路的差异性,协调小区间同频子 信道的发射功率及宏基站的定价,减小同层及跨层的干扰影响,节约家庭用户总发射功率。仿真表明本文SEPCA算法,在付出较低的能量效率代价下,极大地降低了算法的复杂度,间接达到了节能的目的。
| [1] | CHANDRASEKHAR V, ANDREWS J G, GATHERER A. Femtocell networks: a survey[J]. IEEE Communications Magazine, 2008, 46(9): 59 - 67. |
| [2] | SARAYDAR C U, MANDAYAM N B, GOODMAN D J. Pareto efficiency of pricing-based power control in wireless data networks[C]//Wireless Communications and Networking Conference. New Orleans: IEEE, 1999: 231- 235. |
| [3] | SU Tao, ZHENG Wei, LI Wei, et al. Energy efficient power optimization with Pareto improvement in two-tier femtocell networks[C]//Personal Indoor and Mobile Radio Communications. Sydney, Australian: IEEE, 2012: 2512- 2517. |
| [4] | MIAO G, HIMAYAT N, LI G Y, et al. Low-complexity energy-efficient scheduling for uplink OFDMA[J]. IEEE Trans on Commun, 2012, 60(1): 112-120. |
| [5] | 李鹏, 朱宇. 一种异构网络中的斯坦克尔伯格功率控制方法[J]. 太赫兹科学与电子信息学报, 2013(3): 368-376. LI Peng, ZHU Yu. A Stackelberg approach on power control in heterogeneous networks[J]. Information and Electronic Engineering, 2013(3): 368-376. |
| [6] | CHEN Wei, ZHANG Li-li, HE Zhi-yi. Second-order statistics of improved Jakes' models for Rayleigh fading channels[C]//Proceedings of 2007 International Conference on Wireless Communications, Networking and Mobile Computing. Shanghai: IEEE, 2007: 1108-1111. |
| [7] | KANG X, ZHANG R, MOTANI M. Price-based resource allocation for spectrum-sharing femtocell network: a Stackelberg game approach[J]. IEEE Journal on Selected Areas in Commun, 2012, 30(3): 538-549. |
| [8] | ROBERTS S W. Control chart tests based on geometric moving averages[J]. Technometrics, 1959, 42(1): 239-250. |
| [9] | FUDENBURG D, TIROLE J. Game theory[M]. Cambridge, USA: The MIT Press, 1991. |
| [10] | WOLFSTETTER E. Topics in microeconomics: industrial organization, auctions, and incentives[M]. London: Cambridge University Press, 1999: 209-11. |
| [11] | ZHANG Tian-kui, ZENG Zhi-ming, ZHANG Yi-yun. Multi-cell adaptive power allocation scheme based on game theory in OFDMA systems[J]. Journal on Communications, 2008, 29(1): 22-23. |
 2015, Vol. 44
2015, Vol. 44
