2. 电子科技大学物理电子学院 成都 610054
2. School of Physical Electronic, University of Electronic Science and Technology of China Chengdu 610054
As we know, alternating-current plasma display panels(AC PDPs) have great marketability in the large flat-panel display market dueto their fast operating speed and simple manufacturing process[1, 2, 3].Generally, AC PDPs consist of electrodes, barrier ribs, discharge cell,dielectric layers, and a protective layer. The protective layer plays animportant role in the decrease of power consumption and protection frombombardments of numerous particles such as ions, electrons, and metastableatoms.
On the other hand, AC PDPs have some disadvantages,including lower luminous efficacy and higher power consumption than other flatpanel displays such as a liquid crystal display (LCD) or an organic lightemitting diode (OLED)[4]. It is known that MgO is the onlycommercially available protective material of AC PDP presently. Thus, in orderto reduce the electrical power consumption further, it is necessary to develop anew protective material based on MgO with higher SEE yield to reduce the firingvoltage and sustain voltage of AC PDPs[5, 6]. For example, Motoyama etal. obtained formulas for the simple calculation of the secondary electronyield from Hagstrum’s theory, and calculated the secondary electron yieldvalues of BaO and MgO for He, Ne, Ar, Kr, and Xe ions and metastable atoms[7].The impact of Si-doping on the electronic properties of the MgO layer wasstudied in Ref.[8]. Secondary electron emission yield of the Mg1-xSixOin the plasma display panel cell filled with a mixture of Ne and Xe gas wasalso discussed.
In this paper, the electronic structure, band structure,and density of states of the Mg1-xAlxOcrystal are analyzed. Then the secondary electron emission coefficient ($\gamma $)values of Mg1-xAlxO for various gases arecalculated by Hagstrum’s theory. The calculated results show that with theaddition of Al atoms, the $\gamma $values increase,especially in helium gas. 1 Band Structures and Density of States Calculation
The MgO crystal model used in our paper is shown inFigure 1. MgO is NaCl-type crystal with space group of FM-3M. The latticeconstant is 0.421 12 nm, and bond angles are $\alpha = \beta = \gamma $= 90°.
 |
| Fig. 1 Crystal model of MgO |
In order to investigate the band structure and densityof states, the cambridge serial total energy package (CASTEP) simulationprogram is introduced, using the Kohn-Sham formation that is based on thedensity functional theory. The exchange and correlation potentials amongelectrons are corrected by local density approximation (LDA). Firstly, thegeometry optimization of the MgO crystal is performed by the LDA and ultrasoftpseudopotential method. During the calculation, plane-wave cut-off energy is340 eV, k points set in reciprocal space is 6×6×6, and theself-consistent field (SCF) tolerance is 10-6 eV·atom-1. The iteration is repeated until the energy isless than 0.001 meV/atom and root-mean- square (RMS) stress is less than 0.05Gpa. Then, the partial density of states of Mg and O and the total density ofstates of MgO are obtained, respectively.
The structure of Mg1-xAlxOis obtained by replacing Mg atom with Al atom in the cubic rock-salt structure.We set up a 2×2×2 super cell to model the Mg1-xAlxOstructure. For each Mg1-xAlxO super cellwith symmetry P1, the geometrical optimization is performed by the CASTEPsimulation program. In this step, atomic positions are relaxed and optimizedwith a density mixing scheme by using the Pulay method for eigenvaluesminimization. Finally, the energy band structure and density of states of Mg1-xAlxOare obtained. In addition, it is known that LDA pseudopotential calculation mayunderestimate band gap energy, although the estimation of valence band isaccurate. Thus, we amend band gap using scissors operation with a rigid upward shiftof the conduction band with respect to the valence band from the experimentalvalue of the band gap of 0.78 eV. The amendment does not prevent us fromanalyzing our results qualitatively. 2 Secondary Electron Emission Coeffi-Cient Calculation
In order to study the characteristics of Mg1-xAlxOused in AC PDP, the secondary electron emission coefficient of Mg1-xAlxOfor different gases is calculated. As we know, the plasma display dischargecell is very small and the firing voltage of discharge cell is about 200V, andthe priming electrons can’t get enough energy. Hence, it is difficult to formfast electron, and the contribution of fast electron to secondary electron isvery small. According to the theory and experimental results of Hagstrum[9, 10],the mechanism of secondary electron emission consistsof the following two processes: Auger neutralization and Auger deexcitation, asshown in Fig. 2a and Fig. 2b. During our simulation, the bottom of the valenceband and electronic affinity of MgO are defined as zero and 0.85 eV,respectively.
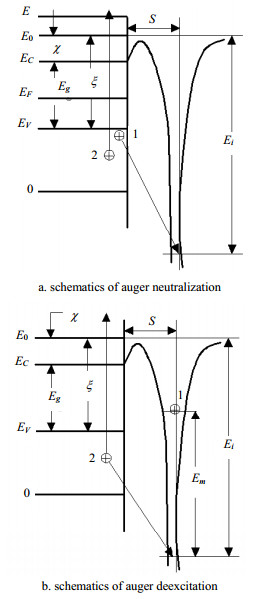 |
| Fig. 2 The mechanism of secondary electron emission |
From Fig. 2a, when electron 1 moves to the ground stateof an atom and electron 2 is excited simultaneously, the energy distribution ${N_i}(E)$of the excited electron could be given by the following expression[7].
| ${N_i}(E) \propto {\rho _0}(E)\int_0^{{E_V}} {\int_0^{{E_V}} {n({E_1})} } n({E_2}) \times \delta (E - {E_1} - {E_2} + {E_0} - {E_i}){\rm{d}}{E_1}{\rm{d}}{E_2} = {\rho _0}(E)T\left[ {\frac{{E + {E_0} - {E_i}}}{2}} \right]$ | (1) |
where$\delta ({\rm{ }})$, $T[E]$, and $n(E)$aredelta function of Dirac, Auger transform function, and valence band electrondensity of states function, respectively. ${\rho _0}(E)$is the statedensity of the excited electron, which is considered proportional to ${(E - {E_C})^{1/2}}$. If $E > {E_0}$,an electron could be excited to escape from the solid surface. Assuming thisescape probability is ${P_e}(E)$is given byexpression (2), we could obtain the expression (3) for the secondary electronyield ${\gamma _N}$caused by Augerneutralization at a distance s.
| ${P_e}(E) = \frac{1}{2}{\left[ {1 - {{\left( {\frac{{{E_0}}}{E}} \right)}^\beta }} \right]^\alpha }E > {E_0}$ | (2) |
| ${\gamma _N} = \frac{{\int_{\max \left\{ {{\alpha _i},1} \right\}}^{{\beta _i}} {P_e^*(x)\sqrt {x - \sigma } {T^*}(x){\rm{d}}x} }}{{\int_{\max \left\{ {{\alpha _i},\sigma } \right\}}^{{\beta _i}} {\sqrt {x - \sigma } {T^*}(x){\rm{d}}x} }}$ | (3) |
where α and β areconstants of 0.248 and 1.0 determined by Hagstrum, respectively. ${\alpha _i} \equiv {E_i}/{E_0}$-1; ${\beta _i} \equiv ({E_i} - 2\xi )/{E_0} + 1$; ${P_e}^*(x) = {(1 - {x^{ - \beta }})^\alpha }/2$. The function ${T^*}(x)$, which is assumed forparabolic band of state density and finite only in ${\alpha _i} < x < {\beta _i}$, is given as follows:
| $\left\{ \begin{array}{l} {T^*}(x) = {(x - {\alpha _i})^2}{\rm{ }}{\alpha _i} < x \le ({\alpha _i} + {\beta _i})/2\\ {T^*}(x) = {({\beta _i} - x)^2}{\rm{ }}({\alpha _i} + {\beta _i})/2 < x \le {\beta _i} \end{array} \right.$ | (4) |
From Fig. 2b, when an ion approaches a solid surface andresonance neutralization occurs, the ion becomes an excited atom. Then, theexcited atom returns to the ground state by Auger deexcitation, unlessresonance ionization occurs with the condition ${E_i} - {E_m} < x$for a smallerdistance s. The process of Auger neutralization, the energy distribution${N'_i}(E)$of the excited electron is given by[7]:
| ${N'_i}(E) \propto {\rho _0}(E)\int_{{\rm{ }}0}^{{\rm{ }}{E_V}} {n({E_2})} \delta ({E_2} - E + {E_m}){\rm{d}}{E_2} = {\rho _0}(E)n(E - {E_m})$ | (5) |
Similar with the process of Auger neutralization, thesecondary electron yield γDcaused by Auger deexcitation can be obtained as follows:
| ${\gamma _D} = \frac{{\int_{\max \{ {E_m} - {E_0},{E_0}\} }^{{E_m} - \xi + {E_0}} {{P_e}(E)\sqrt {E - {E_C}} n(E - {E_m}){\rm{d}}E} }}{{\int_{\max \{ {E_m} - {E_0},{E_C}\} }^{{E_m} - \xi + {E_0}} {\sqrt {E - {E_C}} n(E - {E_m}){\rm{d}}E} }}$ | (6) |
Putting $x \equiv E/{E_0}$and $\sigma \equiv {E_C}/{E_0}$, γDcould be definedby another expression, i.e.
| ${\gamma _D} = \frac{{\int_{\max \{ {\alpha _m},1\} }^{{\beta _m}} {P_e^*(x)\sqrt {x - \sigma } {n^*}(x){\rm{d}}x} }}{{\int_{\max \{ {\alpha _m},\sigma \} }^{{\beta _m}} {\sqrt {x - \sigma } {n^*}(x){\rm{d}}x} }}$ | (7) |
where ${\alpha _m} = {E_m}/{E_0}$,${\beta _m} = ({E_m} - \xi )/{E_0} + 1$. The function ${n^*}(x)$, which is assumed forparabolic band of state density and finite only in ${\alpha _m} < x < {\beta _m}$, is given asfollows:
| $\left\{ \begin{array}{l} {n^*}(x) = {(x - {\alpha _m})^{1/2}}{\rm{ }}{\alpha _m} < x \le ({\alpha _m} + {\beta _m})/2\\ {n^*}(x) = {({\beta _m} - x)^{1/2}}{\rm{ }}({\alpha _m} + {\beta _m})/2 < x < {\beta _m} \end{array} \right.$ | (8) |
Fig. 3a and Fig. 3b show the partial density of states ofMgO. The electronic states of Mg mainly distribute in the valence band andconduction band, and O atoms almost appear in the valence band. The possiblereason is that the valence band is constituted by O-2p with some small peaks ofMg-3s, while conduction band is mainly composed of Mg-3s. In addition, there isobvious a hybrid phenomenon between Mg-O bonds, which means a stronginteraction between the Mg-O constructions.
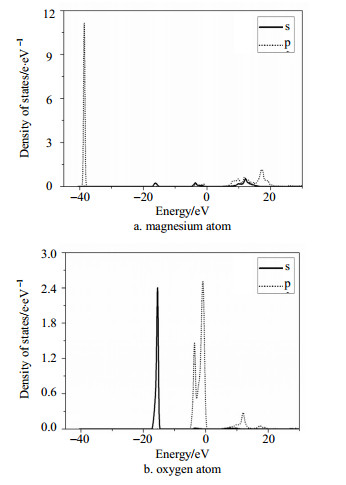 |
| Fig. 3 Partialdensity of states of Mg and O atom for MgO |
Fig. 4a~4e show the total density of states of Mg1-xAlxOwith different Al doping ratios (x=0, 0.125, 0.25, 0.375, 0.5),respectively. The Mg1-xAlxO layer has asmaller band gap than the pure MgO layer. Furthermore, compared with the pureMgO layer, the Mg1-xAlxOlayer has a relatively small band gap energy and large valence bandwidth. The higher the Al concentration is, the smaller the band gap is. Italso can be seen that the density of states of valence band and conduction bandboth have gained a great increase because of the contribution of Al-3p. Thiscan make the electrons of conduction band excite more easily. Combined with theresults from other literatures[11, 12], we think that narrowing ofthe band gap is favorable for the enhancement of secondary emissioncoefficient.
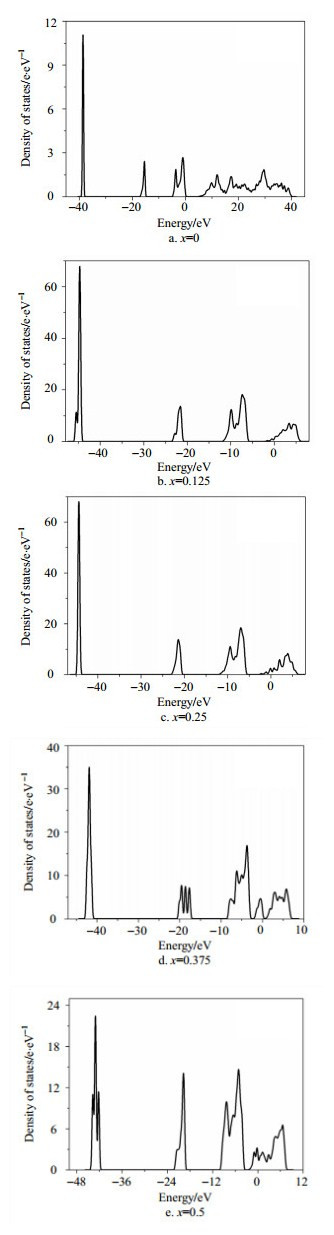 |
| Fig. 4 Thetotal density of states for the Mg1-xAlxO |
The ${\gamma _N}$values of Mg1-xAlxO forall noble gas ions are shown in Tab. 1, which are calculated by the formulasrelevant to Auger neutralization. Wherein, ${E_i}$(He)=24.58 eV, ${E_i}$(Ne)=21.56eV, ${E_i}$(Ar)=15.76 eV, ${E_i}$(Kr)=14.00eV, and ${E_i}$(Xe)=12.13 eV. Weobserve three important phenomena in the calculated results:
1) As Al atoms are doped in MgO crystal, the ${\gamma _N}$value increases in all gases. Especially in He, the maximum of${\gamma _N}$is up to 0.419 1 at the Al doping ratio of 0.375.
2) When the Al doping ratio is 0 and 0.125 in Kr and Xe,it does not meet the conditions of ${E_i}$<2ζ[13, 14].Thus, Auger neutralization does not occur and the ${\gamma _N}$values are zero.
3) There are optimum values of Al doping ratio with thehighest ${\gamma _N}$in various gases.For example, the optimum value of Al doping ratio for He, Ne, and Ar is 0.375.
| Table 1 Secondaryelectron emission coefficient of Mg1-xAlxO based on Auger neutralization |
The γDvaluesof Mg1-xAlxO calculated by the formulasrelevant to Auger deexcitation for various gas ions are shown in Tab. 2, where ${E_m}$(He)=19.81 eV, ${E_m}$(Ne)= 16.61 eV, ${E_m}$(Ar)=11.55 eV, ${E_m}$(Kr)= 9.91 eV, and Em(Xe)=8.31 eV. Mg1-xAlxO almost presents higher γDvaluesthan pure MgO in every gas. As the Al doping ratio increases, the γDincreasesaccordingly and reaches the maximums at Al doping ratio of 0.375 for all gasesexcept for Xe. In He environment, the maximum of γDis up to 0.431 6.
| Table 2 Secondaryelectron emission coefficient of Mg1-xAlxO based onAuger deexcitation |
In this paper, the band structure and density of statesof pure MgO and Mg1-xAlxO protective layerwith different x values have been investigated by using the firstprinciples theory. The results show that with the increase of Al concentration,the band gap energy of Mg1-xAlxO becomessmaller. The secondary electron emission coefficients of both MgO and Mg1-xAlxOprotective layers have also been calculated under different inert gases basedon Auger neutralization and Auger exexcitation.The γ values of Mg1-xAlxOare always higher than those of pure MgO, which can reduce the firing voltageand sustain voltage of AC PDP effectively. Moreover, there are optimum valuesof Al doping ratio with the highest γ value in variousgases based on Auger neutralization and Auger deexcitation.
| [1] | PARK C S, TAE H S, JUNG E Y. Influence of Al2O3 reflective layer under phosphor layer on luminance and luminous efficiency characteristics in alternating-current plasma display panel[J]. Thin Solid Films, 2013, 547: 43-46. |
| [2] | KIM J K. Modification of a driving waveform in an AC plasma display panel with Sc-doped MgO protecting layer[J]. IEEE Trans Electron Devices, 2013, 60(8): 2556-2560. |
| [3] | CHEN Y X, LI Q, HU K, et al. Wall-voltage stability in AC-PDP dielectric barrier discharges[J]. IEEE Trans Plasma Science, 2013, 41(1): 159-164. |
| [4] | LEE T H, CHEONG H W, KWON O, et al. Application of MgCaO cathode layer to plasma display panel for high luminous efficacy[J]. IEEE Trans Electron Devices, 2013, 60(1): 301-304. |
| [5] | AHN S I, LEE S E, RYU S H, et al. A study on the secondary electron emission from Na-ion-doped MgO films in relation to the discharge characteristics of plasma display panels[J]. Thin Solid Films, 2009, 517: 1706-1709. |
| [6] | HA C H, KIM J K, WHANG K W. The operation characteristics of an alternating current plasma display panel with Si-Doped MgO protecting layer[J]. IEEE Trans Electron Devices, 2008, 55(4): 992-996. |
| [7] | YASUSHI M, HIDEOMI M, HIROSHI M. A study of the secondary electron yield γ of insulator cathodes for plasma display panels[J]. IEEE Trans Electron Device, 2001, 48(8): 1568-1574. |
| [8] | 李巧芬, 屠彦, 杨兰兰, 等. PDP放电单元Si掺杂MgO保护层二次电子发射系数理论研究[J]. 真空科学与技术学报, 2010, 30(5): 535-540. LI Qiao-fen, TU Yan, YANG Lan-lan, et al. Calculation of secondary electron emission coefficient of Si doped MgO protective layer for plasma display panel[J]. Chin J Vac Sci Technol, 2010, 30(5): 535-540. |
| [9] | HAGSTRUM H D. Theory of Auger ejection of electrons from metals by ions[J]. Phys Rev, 1954, 96(2): 336-365. |
| [10] | HAGSTRUM H D. Theory of Auger neutralization of ions at the surface of a diamond-type semiconductor[J]. Phys Rev, 1961, 122(1): 83-113. |
| [11] | AHN S G, YOON S H, KIM Y S. Secondary electron emission characteristics of MgO-ZnO thin film layer for AC PDP[J]. Thin Solid Films, 2009, 517: 4027-4030. |
| [12] | LI Q F, TU Y, TONLNER H, et al. Plasma discharge efficiency increase by using a small bandgap protective layer material-first-priciples study for Mg1-xZnxO[J]. J Appl Phys, 2011, 109: 093307. |
| [13] | SAHNI O, LANZA C. Importance of the dependence of the secondary electron emission coefficient on E/p0 for Paschen breakdown curves in ac plasma panels[J]. J Appl Phys, 1976, 47(4): 1337-1340. |
| [14] | ABOELFOTOH M O, LORENZEN J A. Influence of secondary-electron emission from MgO surfaces on voltage-breakdown curves in Penning mixtures for insulated-electrode discharge[J]. J Appl Phys, 1977, 48(11): 4754-4759. |
 2015, Vol. 44
2015, Vol. 44
