2. 电子科技大学能源科学与工程学院 成都 611731;
3. 电子科技大学微电子与固体电子学院 成都 610054
2. School of Energy Science and Engineering, University of Electronic Science and Technology of China Chengdu 611731;
3. School of Microelectronics and Solid-State Electronics, University of Electronic Science and Technology of China Chengdu 610054
在功率电子电路中,DC-DC变换器是一个典型的非线性动力学系统,存在分岔、混沌等丰富的非线性现象[1]。这些非线性现象将会影响DC-DC变换器的整体性能,因此通过DC-DC变换器的非线性动力学研究,更好地理解其工作机理,对实际工程应用具有理论指导意义。
许多学者对二阶DC-DC变换器进行了大量的研究[2, 3, 4],但是二阶DC-DC变换器的输入电流是不连续的,它具有高EMI噪声以及大电容电流应力。20世纪70年代后期陆续发明了Cuk变换器[5]和SEPIC变换器[6],但是SEPIC转换器不能给输出电容提供连续的充电电流,Cuk变换器具有相反极性的电压输出,这些特性限制了上述高阶变换器的应用范围。高阶变换器还有其他多种形式的拓扑,如新能源并网系统中的Z源变换器[7, 8],应用于太阳能光伏系统的superbuck变换器[9, 10]。文献[11]通过电路实验研究了VF-superbuck变换器中的分岔与混沌现象。文献[12]建立了CF-superbuck变换器的平均和小信号模型,分析了系统的动力学特性。但是CF-superbuck变换器是典型的高阶变换器,具有复杂的非线性动力学特性。
本文对峰值电流控制CF-superbuck变换器的非线性动力学行为进行详细地研究。基于CF-superbuck变换器的状态方程建立了CF-superbuck变换器的离散迭代映射模型,以反馈回路中的参考电流为分岔参数得到了变换器电感电流的分岔图,分析了系统非线性动力学的演化过程。研究结果表明基于峰值电流控制CF-superbuck变换器存在复杂的分岔和混沌行为。本文详细分析了系统分岔的过程及其产生的机理,给出了CF-superbuck变换器的电路仿真和实验结果,验证了理论分析的正确性。
1 峰值电流控制高阶变换器峰值电流控制CF-superbuck变换器的电路结构如图 1所示。
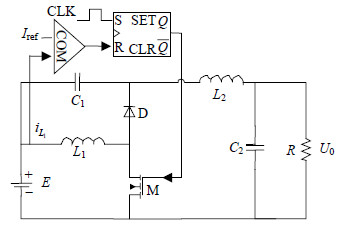 |
| 图 1 峰值电流控制CF-superbuck变换器 |
图 1中,E为输入电压,M为功率开关管,L1、L2为电感,C1、C2为电容,R为负载电阻;D为二极管,其开关速度与功率开关管相同,通常采用快恢复二极管。为了便于分析电路的工作原理,对该拓扑作一些近似:功率开关管和二极管是理想开关器件,即瞬时地导通和截止,导通时压降为零,截止时漏电流为零;电容、电感是理想元件,即电感工作在线性区且未磁饱和,寄生电阻为零,电容的等效串联电阻为零;输入直流电压E是恒压源,其内阻为零;变换器工作于电感电流连续模式(CCM)。
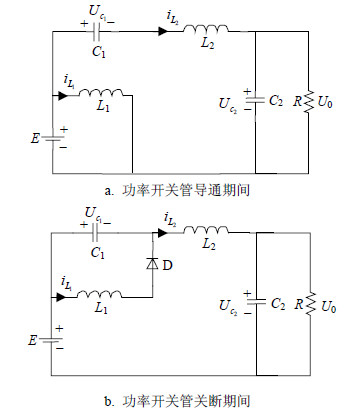 |
| 图 2 CF-superbuck变换器的电路结构 |
CF-superbuck变换器的电路结构如图 2所示,图中,iL1为电感L1上流过的电流,Uo为负载电阻R两端的电压。当时钟脉冲CLK开始工作时,功率开关管M栅极输入为高电平,功率开关管M导通,电感电流iL1线性上升。当电感电流iL1增加至参考电流Iref时,比较器复位触发器,功率开关管M关断,电感电流iL1线性下降,直至下一个时钟脉冲开始时,功率开关管M再次导通。
2 高阶变换器的动力学模型基于峰值电流控制CF-superbuck变换器工作于CCM模式,电路存在两种工作状态,即功率开关管导通电感L1电流上升阶段和功率开关管关断电感L1电流下降阶段。功率开关管导通期间,CF-superbuck变换器的电路结构如图 2a所示,其状态空间方程为:
| $\left\{ \begin{array}{l} \frac{{{\rm{d}}{i_{{L_1}}}}}{{{\rm{d}}t}} = \frac{E}{{{L_1}}}\\ \frac{{{\rm{d}}{i_{{L_2}}}}}{{{\rm{d}}t}} = \frac{{E - {U_{{C_1}}} - {U_{{C_2}}}}}{{{L_2}}}\\ \frac{{{\rm{d}}{U_{{C_1}}}}}{{{\rm{d}}t}} = \frac{{{i_{{L_2}}}}}{{{C_1}}}\\ \frac{{{\rm{d}}{U_{{C_2}}}}}{{{\rm{d}}t}} = \frac{{{i_{{L_2}}}}}{{{C_2}}} - \frac{{{U_{{C_2}}}}}{{R{C_2}}} \end{array} \right.$ | (1) |
功率开关管关断期间,CF-superbuck变换器的电路结构如图 2b所示,其状态空间方程为:
| $\left\{ \begin{array}{l} \frac{{{\rm{d}}{i_{{L_1}}}}}{{{\rm{d}}t}} = \frac{{{U_{{C_1}}}}}{{{L_1}}}\\ \frac{{{\rm{d}}{i_{{L_2}}}}}{{{\rm{d}}t}} = \frac{{E - {U_{{C_1}}} - {U_{{C_2}}}}}{{{L_2}}}\\ \frac{{{\rm{d}}{U_{{C_1}}}}}{{{\rm{d}}t}} = \frac{{{i_{{L_2}}} - {i_{{L_1}}}}}{{{C_1}}}\\ \frac{{{\rm{d}}{U_{{C_2}}}}}{{{\rm{d}}t}} = \frac{{{i_{{L_2}}}}}{{{C_2}}} - \frac{{{U_{{C_2}}}}}{{R{C_2}}} \end{array} \right.$ | (2) |
该变换器的状态方程可写为:
| ${\bf{\dot x}} = {{\bf{A}}_1}{\bf{x}} + {{\bf{B}}_1}E$ | (3) |
| ${\bf{\dot x}} = {{\bf{A}}_2}{\bf{x}} + {{\bf{B}}_2}E$ | (4) |
式中,${\bf{x}} = {[\begin{array}{*{20}{c}} {{i_{{L_1}}}}&{{i_{{L_2}}}}&{{U_{{C_1}}}}&{{U_{{C_2}}}} \end{array}]^{\rm{T}}}$为系统的状态变量;A1、A2为系统的参数矩阵;B1、B2为系统的输入矩阵;且A1、A2、B1、B2都是常数矩阵,分别为:
| ${{\bf{A}}_1} = \left( {\begin{array}{*{20}{c}} 0&0&0&0\\ 0&0&{ - \frac{1}{{{L_2}}}}&{ - \frac{1}{{{L_2}}}}\\ 0&{\frac{1}{{{C_1}}}}&0&0\\ 0&{\frac{1}{{{C_2}}}}&0&{ - \frac{1}{{R{C_2}}}} \end{array}} \right),{B_1} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{L_1}}}}\\ {\frac{1}{{{L_2}}}}\\ 0\\ 0 \end{array}} \right]$ |
| ${A_2} = \left( {\begin{array}{*{20}{c}} 0&0&{\frac{1}{{{L_1}}}}&0\\ 0&0&{ - \frac{1}{{{L_2}}}}&{ - \frac{1}{{{L_2}}}}\\ { - \frac{1}{{{C_1}}}}&{\frac{1}{{{C_1}}}}&0&0\\ 0&{\frac{1}{{{C_2}}}}&0&{ - \frac{1}{{R{C_2}}}} \end{array}} \right),{B_2} = \left[ {\begin{array}{*{20}{c}} 0\\ {\frac{1}{{{L_2}}}}\\ 0\\ 0 \end{array}} \right]$ |
采用闪频采样方法求式(3)和式(4)的离散迭代映射方程。令dn为第n个周期T的占空比,在每nT时刻进行采样,记Xn=X(nT),n=1,2,3,---,T为时钟脉冲周期。利用线性系统理论中状态微分方程的求解方法[13],可得在(n+dn)T时刻系统的状态向量${X_{n + {d_n}}} = X{\rm{(}}nT{\rm{ + }}{d_n}T{\rm{)}}$,有:
| ${X_{n + {d_n}}} = {{\rm{e}}^{{A_1}{d_n}T}}{X_n} + ({{\rm{e}}^{{A_1}{d_n}T}} - E){A_1}^{ - 1}{B_1}$ | (5) |
在(n+1)T时刻系统的状态向量Xn+1=X(nT+T),有:
| ${X_{n + 1}} = {{\rm{e}}^{{A_2}(1 - {d_n})T}}{{\rm{e}}^{{A_1}{d_n}T}}{X_n} + {{\rm{e}}^{{A_2}(1 - {d_n})T}}({{\rm{e}}^{{A_1}{d_n}T}} - E){A_1}^{ - 1}{B_1}[{{\rm{e}}^{{A_2}(1 - {d_n})T}} - E]{A_2}^{ - 1}{B_2}$ | (6) |
系统的异步切换函数为:
| $S({X_n},{d_n}) = {i_{{L_1}}} - {I_{{\rm{ref}}}} = {K^{\rm{T}}}X(nT + {d_n}T) - {I_{{\rm{ref}}}}{K^{\rm{T}}}[{{\rm{e}}^{{A_1}{d_n}T}}X(nT) + ({{\rm{e}}^{{A_1}{d_n}T}} - E){A_1}^{ - 1}{B_1}E] - {I_{{\rm{ref}}}}$ | (7) |
当$S({X_n},{d_n}) = 0$时,功率开关管M截止,解此方程,即可求出占空比dn,但该方程是超越方程,所以只能通过数值方法求解。
3 数值仿真
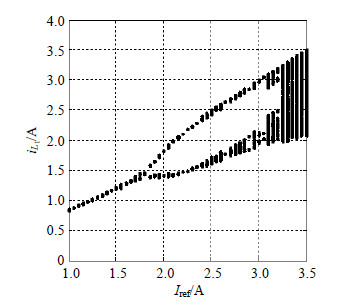 |
| 图 3 以参考电流Iref为分岔参数电感电流iL1的分岔图 |
当CF-superbuck变换器的系统参数发生变化时,系统具有非常复杂的非线性动力学特性。本节讨论工作于CCM模式下系统的非线性动力学演化过程。变换器的电路参数分别选取为E=10 V,T=20 μs,L1=100 μH,L2=1 mH,C1=1 μF,C2=90 nF,R=15 Ω。以变换器反馈回路中参考电流Iref为分岔参数,变换器电感电流iL1的分岔图如图 3所示。
从图 3中可以发现,当参考电流Iref在1~3.5 A之间变化时,系统经历从稳态到分岔态,再到混沌态的动力学行为演化过程。当Iref在1~1.78 A之间变化时系统处于稳态,在Iref=1.78 A时系统结束周期1态进入倍周期分岔态。随着参考电流Iref继续增大,系统发生了周期2到周期3的分岔,最后进入混沌态。
4 电路仿真和实验验证为了进一步完善对CF-superbuck变换器非线性动力学的研究,通过PSIM电路仿真和实验来验证峰值电流控制CF-superbuck变换器理论分析的正确性。
图 4为电路仿真得到的电感电流iL1和电容电压Uc2的时域波形图及其相图。图 5为与电路仿真相对应的实验波形图。
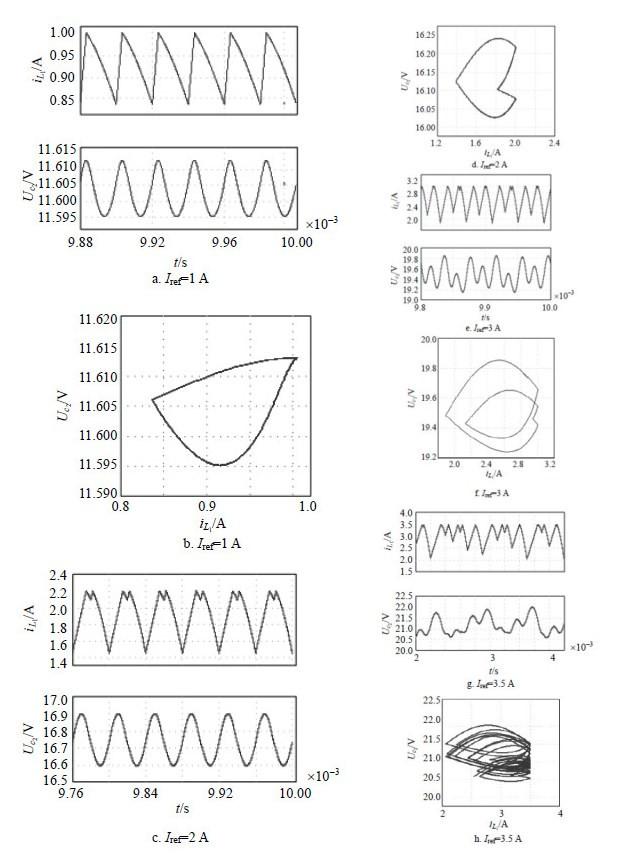 |
| 图 4 PSIM电路仿真得到的电感电流iL1和电容电压UC2的时域波形图及其相图 |
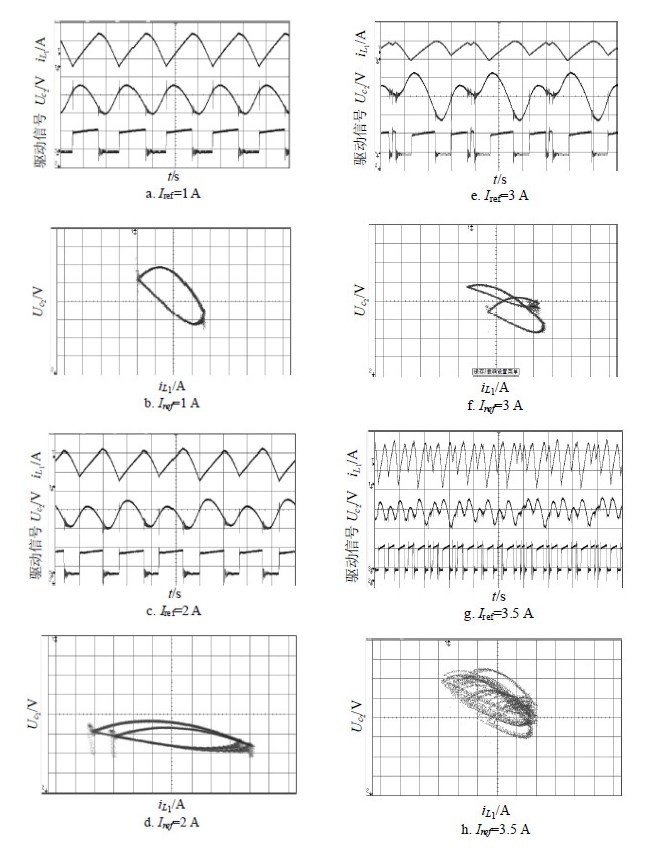 |
| 图 5 实验波形图 |
由图 4和图 5可知,当参考电流Iref为1 A时,电感电流iL1和电容电压UC2的时域波形图表明CF-superbuck变换器处于周期1态,其相图中只有一个环。当参考电流Iref为2 A时,CF-superbuck变换器处于周期2态;当参考电流Iref增大到3 A时,变换器处于周期3态;随着参考电流Iref的继续增大,系统最终进入混沌态。图 4和图 5所展示的系统非线性动力学演化过程与图 3中所呈现的整体趋势完全吻合。因此,电路仿真和实验验证了上述理论和数值分析的正确性。通过上述方法,研究了高阶变换器分别处于稳态,分岔态和混沌态的非线性现象,为高阶变换器的非线性动力学研究提供了依据。在实际的电路设计中,应合理确定系统的控制参数,避免系统进入分岔态和混沌态,使系统工作于稳态。
5 结 论本文建立了峰值电流控制CF-superbuck变换器的理论模型,通过数值仿真研究了高阶变换器的非线性动力学特性,以参考电流为分岔参数,观察了系统从周期态到分岔态直至混沌态的非线性动力学演化过程。当参考电流取不同的值时电路仿真和实验得到的电感电流和电容电压的时域波形图及其相图,验证了理论分析和数值仿真的正确性。通过对CF-superbuck变换器的非线性动力学研究,更好地理解高阶变换器中复杂非线性现象的机理,对高阶变换器的工程应用具有重要的指导意义。
| [1] | ZHOU X, LI J. Chaos Phenomena in DC-DC converter and Chaos control[J]. Procedia Engineering, 2012, 29: 470-473. |
| [2] | YESODHA V, KAVIPRIYA R, JOSHNA T S, et al. Analysis of chaos and bifurcation in DC-DC converter using matlab[C]//International Conference on Circuits, Power and Computing Technologies. Nagercoil: IEEE, 2013: 481-487. |
| [3] | HE J, ZHENG X, WANG W. Terminal sliding mode control for buck converter with chaos[C]//7th International Power Electronics and Motion Control Conference. Harbin: IEEE, 2012, 3: 1532-1535. |
| [4] | NATSHEH A N, KETTLEBOROUGH J G, JANSON N B. Experimental study of controlling chaos in a DC-DC boost converter[J]. Chaos, Solitons & Fractals, 2009, 40(5): 2500-2508. |
| [5] | CUK S, MIDDLEBROOK R D. A new optimum topology switching DC-to-DC converter[C]//Power Electronics Specialists Conference. Palo Alto: IEEE, 1977(1): 160-179. |
| [6] | ERICKSON R W, MAKSIMOVIC D. Fundamentals of power electronics[M]. New York: Springer, 2001. |
| [7] | 戚振彪, 张兴, 田新全, 等. 基于Z源逆变器的光伏发电系统研究[J]. 电力电子技术, 2009, 43(12): 40-42. QI Zhen-biao, ZHANG Xing, TIAN Xin-quan, et al. Study of Z-source inverter for grid-connected PV systems[J]. Power Electronics, 2009, 43(12): 40-42. |
| [8] | 向俊杰, 毕闯, 向勇, 等. 峰值电流控制同步开关Z源变换器的动力学研究[J]. 物理学报, 2014, 63(12): 120507. XIANG Jun-jie, BI Chuang, XIANG Yong, et al. Dynamical study of peak-current-mode controlled synchronous switching Z-source converter[J]. Acta Physica Sinica, 2014, 63(12): 120507. |
| [9] | KARPPANEN M, ARMINEN J, SUNTIO T, et al. Dynamical modeling and characterization of peak-current-controlled superbuck converter[J]. IEEE Transactions on Power Electronics, 2008, 23(3): 1370-1380. |
| [10] | SUNTIO T, LEPPAAHO J, HUUSARI J, et al. Issues on solar-generator interfacing with current-fed MPP-tracking converters[J]. IEEE Transactions on Power Electronics, 2010, 25(9): 2409-2419. |
| [11] | 毕闯, 张千, 向勇, 等. 峰值电压反馈Superbuck变换器中分岔与混沌的实验研究[J]. 电子与信息学报, 2013, 35(9): 2261-2265. BI Chuang, ZHANG Qian, XIANG Yong, et al. Experiment research of bifurcation and chaos of peak- voltage-feedback superbuck converter[J]. Journal of Electronics & Information Technology, 2013, 35(9): 2261-2265. |
| [12] | LEPPAAHO J, SUNTIO T. Dynamic characterist ics of current-fed superbuck converter[J]. Transactions on Power Electronics, 2011, 26(1): 200-209. |
| [13] | 郑大钟. 线性系统理论[M]. 北京: 清华大学出版社, 2002. ZHENG Da-zhong. Linear system theory[M]. Beijing: Tsinghua University Press, 2002. |
 2015, Vol. 44
2015, Vol. 44
