2. 中国电子科技集团第24研究所 重庆 南岸区 400060;
3. 西南电子技术研究所 成都 610036
2. NO.24 Research Institute of China Electronics Technology Group Corporation Nan'an Chongqing 400060;
3. Southwest China Institute of Electronic Technology Chengdu 610036
PCB板是电子设备的核心部件,由印制板(基板)和安装在板上的各类元器件构成。由于元器件数量多、形状复杂、大小不一,在利用有限元法进行PCB板的动态特性分析时,会导致分网过程复杂,网格和节点数量巨大。特别是在进行设备整机(系统级)动态特性分析时,要详细考虑各类元器件进行详细建模几乎不可能。因此需要对PCB板进行等效建模,即忽略(或部分忽略)板上元器件,以使分网过程能够进行,且模型规模得到控制[1, 2, 3, 4]。
国内外学者围绕PCB板的等效建模做了大量的研究。文献[5]提出利用区域等效来建立PCB板的有限元模型,但当板上元器件数目众多且分布不均时,划分区域太多,导致分网过程复杂。文献[6]研究了PCB板的5种等效建模方法,其中4种方法都不同程度忽略了元器件质量与刚度的影响;文献[7]将PCB板上小元器件质量均布在基板上,大元器件简化为集中质量点;文献[8]提出了PCB板在动态分析时,其等效模型等效刚度的一种计算方法,但未给出具体的适用范围。
鉴于目前各类等效方法的局限,本文根据工程应用需求,提出一种基于等效杨氏模量的等效建模方法。该方法以等效前后PCB板的固有频率相等为原则,将实际PCB板等效为均质、等厚的光板。利用单位杨氏模量模型,推导出第i阶等效模型的杨氏模量。基于最小二乘法,求得多阶频率下等效杨氏模量表达式。把等效杨氏模量和密度赋予等效模型,将使整机分析分网过程大大简化,网格数量大幅度减少,同时能有效地保证等效前后固有频率不变。
1 PCB板等效建模方法 1.1 等效建模基本思路工程上常见的PCB板如图 1a所示,包含基板及安装在基板上的电阻、电容、功能芯片、插槽和接口等部件,由于插槽刚度较低,电阻、电容等元件尺寸较小,在设备系统级动态分析时可忽略它们的局部动态性能,可将原PCB板等效为如图 1b所示的均匀密度的等厚板,并将等效后的PCB板用于电子设备整机的动态分析。
 | 图 1 PCB板结构模型图 |
PCB板的等效原则是保证等效前后固有频率不变。实现方法为:1) 保持等效模型的长宽尺寸和厚度与等效前的基板相同;2) 等效模型材料的泊松比与基板相同,并将元器件质量均匀分布在等效板上,即保持等效模型为均质、等厚的薄板;3) 通过改变等效模型的材料杨氏模量来保证等效前后固有频率相同。因此可建立等效关系为:
| $\left\{ \begin{array}{l} {f_{{\rm{real}}}}(V,E,\rho ,\mu ) \approx {f_{{\rm{equi}}}}(V,{E_{{\rm{equi}}}},{\rho _{{\rm{equi}}}},\mu )\\ {\rho _{{\rm{equi}}}} = \frac{{{M_0}}}{V} \end{array} \right.$ | (1) |
式中,f 为固有频率;V为几何尺寸;E为杨氏模量;ρ为密度;μ为泊松比;M0为原PCB板质量;下标real和equi分别表示原模型和等效模型。
从式(1)可以看出,等效后仅有Eequi为未知,即等效模型的弹性模量,称为等效杨氏模量。
1.2 等效杨氏模量推导根据振动理论[9],结构自由振动特征方程为:
| $\left| {K - {\omega ^2}M} \right| = 0$ | (2) |
式中,K为刚度矩阵;M为质量矩阵;$\omega $为固有频率。
由式(2)得到原PCB板第i阶模态方程为:
| $(K - \omega _i^2M){u_i} = 0$ | (3) |
式中,${\omega _i}$为原来PCB板第i阶固有频率;ui为第i阶振型。
由式(3)可计算得到原PCB板第i阶固有频率${({\omega _i})_{{\rm{real}}}}$和相应的振型${({u_i})_{{\rm{real}}}}$。
为求得等效杨氏模量,首先建立单位杨氏模量模型,即满足等效原则式(1)和式(2),且E=1的模型。根据式(3)可求得单位杨氏模量模型的模态方程为:
| $({K_{{\rm{us}}}} - ({\omega _i})_{{\rm{us}}}^2{M_{{\rm{us}}}}){({u_i})_{{\rm{us}}}} = 0$ | (4) |
式中,Kus为单位杨氏模量模型的刚度矩阵;Mus为质量矩阵;下标us表示单位杨氏模量模型。
由式(4)左乘$({u_i})_{{\rm{us}}}^{\rm{T}}$,整理后可得:
| $({u_i})_{{\rm{us}}}^{\rm{T}}{K_{{\rm{us}}}}{({u_i})_{{\rm{us}}}} = ({\omega _i})_{{\rm{us}}}^2({u_i})_{{\rm{us}}}^{\rm{T}}{M_{{\rm{us}}}}{({u_i})_{{\rm{us}}}}$ | (5) |
根据有限元理论[10],对于均匀等厚板,刚度矩阵和单位杨氏模量刚度矩阵成正比,即有:
| ${K_{{\rm{equi}}}} = {E_{{\rm{equi}}}}{K_{{\rm{us}}}}$ | (6) |
由等效原则式(2)可知,等效模型质量矩阵与单位杨氏模量质量矩阵相等,即有:
| ${M_{{\rm{equi}}}} = {M_{{\rm{us}}}}$ | (7) |
根据振动理论[11],单位杨氏模量模型的振型(ui)us和PCB板等效模型的振型(ui)equi相同。由于模态阶数不同,等效杨氏模量不同,用(Ei)equi表示第i阶模态的等效杨氏模量,因此等效模型的模态方程可表示为:
| ${\kern 1pt} {({E_i})_{{\rm{equi}}}}({u_i})_{{\rm{us}}}^{\rm{T}}{K_{{\rm{us}}}}{({u_i})_{{\rm{us}}}} = {\kern 1pt} ({\omega _i})_{{\rm{real}}}^2({u_i})_{{\rm{us}}}^{\rm{T}}{M_{{\rm{us}}}}{({u_i})_{{\rm{us}}}}$ | (8) |
将式(5)代入式(8),可得:
| ${({E_i})_{{\rm{equi}}}}({\omega _i})_{{\rm{us}}}^{\rm{2}} = ({\omega _i})_{{\rm{real}}}^{\rm{2}}$ | (9) |
将式(9)整理,可得(Ei)equi的表达式为:
| ${({E_i})_{{\rm{equi}}}} = \frac{{({\omega _i})_{{\rm{real}}}^2}}{{({\omega _i})_{{\rm{us}}}^2}}$ | (10) |
式(10)等号右边的所有参数为已知,因此可利用该式求解等效模型第i阶模态的杨氏模量。工程上一般关心结构的低阶频率,特别是基频,所以通过式(10)求得的PCB板第一阶模态等效杨氏模量已能满足工程应用需求。
1.3 多阶频率下等效杨氏模量推导当同时考虑多阶频率下的等效杨氏模量时,式(10)不再适用。为减小等效模型与实际模型固有频率的相对误差,利用最小二乘法,建立前n阶频率相对误差为:
| $y = {\sum\limits_{i = 1}^n {\left[ {\frac{{{{({\omega _i})}_{{\rm{real}}}} - {{({\omega _i})}_{{\rm{equi}}}}}}{{{{({\omega _i})}_{{\rm{real}}}}}}} \right]} ^2}$ | (11) |
式中,y为频率的相对误差,实际上是等效模型第i阶频率等效杨氏模量与考虑多阶频率时的等效杨氏模量之间的相对误差,所以式(11)中频率参数可由杨氏模量参数代替得到:
| ${y^*} = {\sum\limits_{i = 1}^n {\left[ {\frac{{{{({E_i})}_{{\rm{equi}}}} - {E_{{\rm{equi}}}}}}{{{{({E_i})}_{{\rm{equi}}}}}}} \right]} ^2}$ | (12) |
式中,${E_{{\rm{equi}}}}$为考虑多阶频率的杨氏模量。
为了使${y^*}$的值最小,需满足:
| $\frac{{\partial {y^*}}}{{\partial {E_{{\rm{equi}}}}}} = 2\sum\limits_{i = 1}^n {\frac{{{E_{{\rm{equi}}}} - {{({E_i})}_{{\rm{equi}}}}}}{{{{({E_i})}_{{\rm{equi}}}}}}} = 0$ | (13) |
由式(13)可求得多阶频率下的等效杨氏模量为:
| ${E_{{\rm{equi}}}} = \frac{{n\prod\limits_{j = 1}^n {{{({E_j})}_{{\rm{equi}}}}} }}{{\sum\limits_{i = 1}^n {\frac{{\prod\limits_{j = 1}^n {{{({E_j})}_{{\rm{equi}}}}} }}{{{{({E_i})}_{{\rm{equi}}}}}}} }}$ | (14) |
由式(14)可知,多阶频率下等效杨氏模量是由每阶模态的等效杨氏模量共同决定的,该求解方法是一种均匀化方法。
当n=1时,式(14)可化简为:
| ${E_{{\rm{equi}}}} = {({E_1})_{{\rm{equi}}}}$ | (15) |
式(15)与式(11)相同,表明多阶频率下的等效杨氏模量对单阶频率等效也同样适用。
从PCB板的等效建模方法可看出,当PCB板上元器件越小,分布越均匀,等效前后频率误差越小,等效效果越好。
2 元器件对等效杨氏模量的影响分析元器件与PCB之间的接触面积、元器件高度对等效杨氏模量都有一定影响,本文以图 2所示算例进行说明。设PCB板尺寸0.2 m×0.15 m×0.002 m,材料杨氏模量22 GPa,泊松比0.28,密度1 850 kg/m3。元器件位于板中央,杨氏模量26.5 GPa,泊松比为0.42,密度4 600 kg/m3。板的4个角点固定。等效模型尺寸为0.2 m×0.15 m×0.002 m,泊松比0.28。
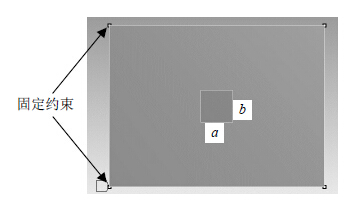 | 图 2 PCB板结构模型示意图 |
元器件与PCB间的接触面积不同,结构的刚度和质量分布不同,从而影响等效杨氏模量。对于图 2所示模型,利用单阶频率等效法,分别取不同的接触面积S(S=a×b,见图 2),等效杨氏模量Eequi与S的关系如图 3所示。
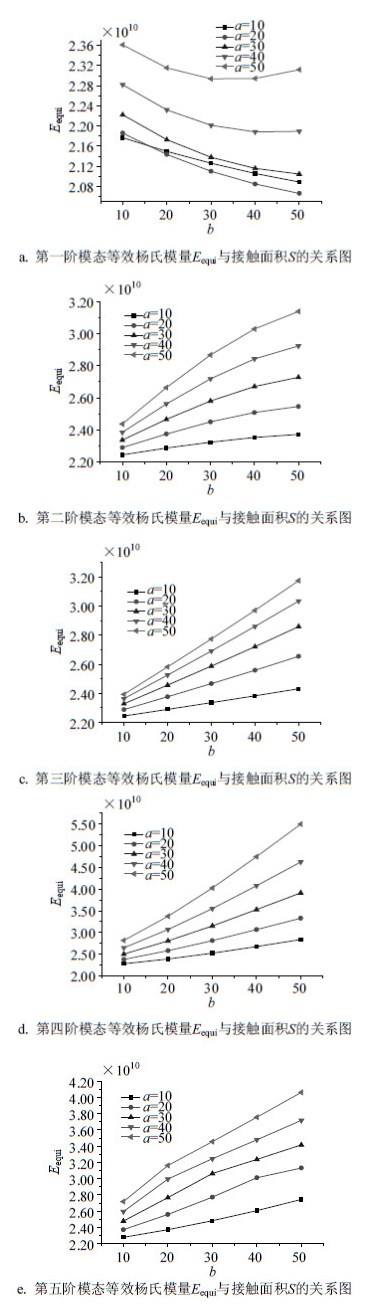 | 图 3 等效杨氏模量Eequi与接触面积S的关系图 |
从图 3可看出:1) 对于第一阶模态,当a一定时,随着b增加,等效杨氏模量的变化规律不同;当b一定时,随着a增加,等效杨氏模量总体呈上升趋势,这主要是由于板结构一阶模态振幅的最大位置位于板中央,导致元器件所在位置是振动薄弱位置,且元器件的长边方向与PCB长边方向一致时,频率越高,导致等效杨氏模量越高;2) 对于第二到第五阶模态,当a一定时,随着b增加,等效杨氏模量上升;当b一定时,随着a增加,等效杨氏模量也上升。这主要是由于a或b的增加,增大了元器件与板间的接触面积S,相当于增加了它们间的接触刚度,导致整体结构刚度增加;3) 各阶模态等效杨氏模量的变化规律不同,说明接触面积S对每阶模态等效杨氏模量影响不同。
利用一阶等效杨氏模量作为等效模型的杨氏模量,等效模型频率相对误差$\delta $与接触面积S的关系如图 4所示。
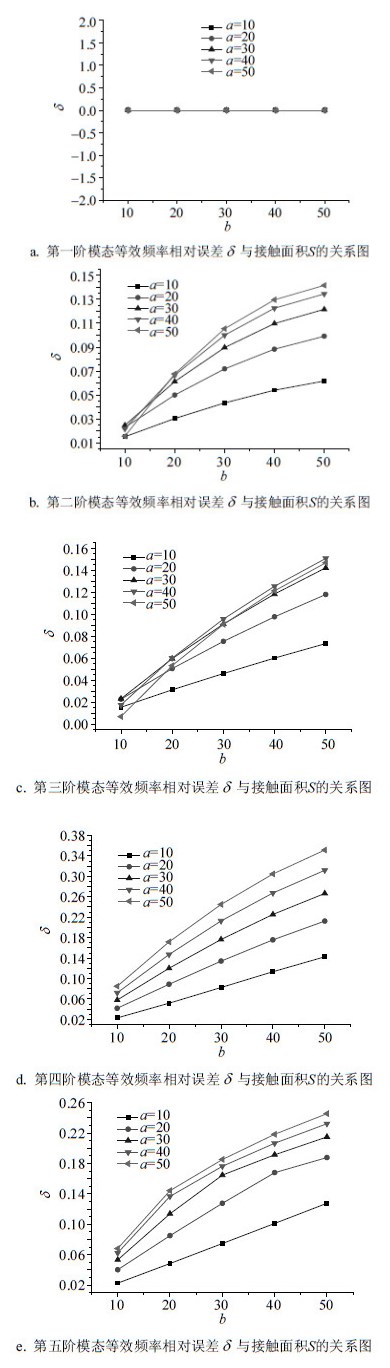 | 图 4 等效频率相对误差$\delta $与接触面积S的关系 |
从图 4可以看出:1) 一阶模态频率相对误差接近于0,说明等效结构和原结构的一阶频率非常吻合。由于工程中常常关心结构的一阶模态,因此可满足大多数工程需要。2) 一阶频率等效时,其他每阶频率的误差变化规律不同,说明结构模型每阶频率对接触面积S变化引起的刚度和质量的分布的灵敏度不同,当接触面积S较大时,第二到第五阶频率误差很大,且随着接触面积S的变化而变化,说明元器件接触面积越小,频率相对误差越小,等效效果越好。
2.2 元器件高度对等效杨氏模量的影响利用单阶频率等效方法,分别取不同的元器件高度,计算得到等效杨氏模量Eequi与元器件高度h的关系如图 5所示。
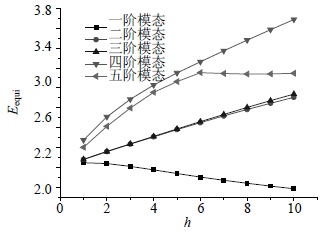 | 图 5 等效杨氏模量Eequi与元器件高度h的关系图 |
从图 5可看出,随着元器件质心远离PCB板,等效杨氏模量变化较复杂,一阶频率等效刚度以类似直线下降变化,第二到第五阶频率等效刚度总体呈上升趋势。采用一阶频率等效的等效刚度,等效模型的频率相对误差$\delta $如图 6所示。
从图 6可以看出,1) 单阶频率等效时,一阶频率相对误差非常小;2) 第二到第五阶频率相对误差,随着高度h的增加而呈现上升趋势,说明元器件高度越低,等效效果越好。
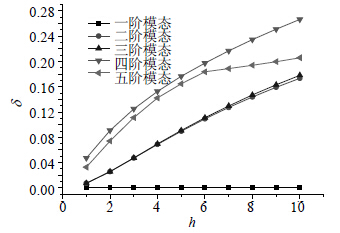 | 图 6 等效频率相对误差$\delta $与元器件件高度h的关系图 |
本文利用ANSYS软件对某电源模块PCB板进行动态分析,以验证等效建模方法的有效性。PCB板模型及等效模型如图 7所示。PCB板杨氏模量为
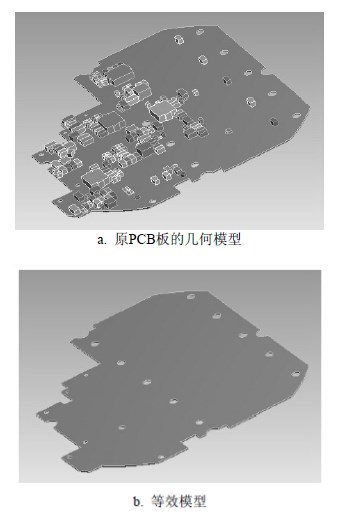 | 图 7 电源模块PCB板几何模型及等效模型图 |
22 GPa,泊松比为0.28,密度为1 850 kg/m3。原PCB板采用大小为0.001 2 m的20节点186单元和10节点187单元,共217 124个节点和125 590个单元。等效板采用大小为0.001 2 m的10节点187单元,共167 536个节点和84 783个单元。可见,等效后PCB板有限元模型的规模大大减小,而且划分网格非常容易。
根据工程需要,考虑前二阶频率等效。计算得到等效杨氏模量42.152 GPa,密度3 237.6 kg/m3。等效模型的各阶频率误差如表 1所示。
| 表1 等效模型频率相对误差表 |
由表 1可以看出,等效模型的前两阶模态频率和原PCB模型频率相对误差在5%以内,能满足工程应用精度要求;两阶频率相对误差相差很接近,说明多阶频率等效方法是一种均匀化方法,与理论推导一致。
用等效模型代替原PCB板进行电源整机建模,整机模型及有限元模型如图 8所示。与原来模型相比,等效后模型节点数量减少49 588个,单元数量减少40 807个。
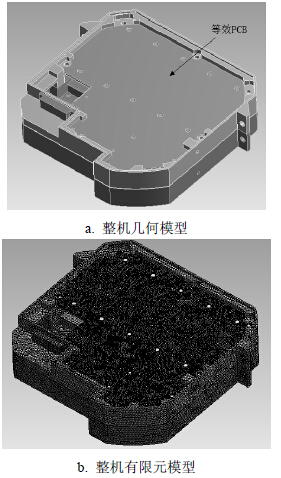 | 图 8 电源模块整机模型及其等效后模型图 |
前两阶频率及相对误差$\delta $如表 2所示。
| 表2 采用等效PCB板的电源频率及其相对误差表 |
从图 8和表 2可以看出,采用等效模型后的有限元模型更简单,划分网格更容易,分析时间更短,且频率的相对误差均小于3%,既能满足工程应用需要,又说明了该等效方法的有效性。
4 结束语基于单位杨氏模量模型,对于带有多种小元器件的PCB板,本文提出一种PCB板动态分析等效建模方法。该方法先将原PCB板简化为等厚度的板,由质量相等原则得到等效密度,并且对单阶频率等效杨氏模量进行了推导,然后基于最小二乘法,求得了多阶频率下等效杨氏模量的表达式。分析了元器件与PCB间接触面积和元器件高度对等效杨氏模量的影响。应用实例表明,采用本文的PCB板等效建模方法,能大大简化有限元模型,同时能有效地保证工程上要求的计算精度,因此对于仪器仪表的系统级分析具有很高的实际应用价值。
| [1] | 李晓明, 吕善伟, 高泽溪, 等. PCB及元件的温度场有限元分析[J]. 北京航空航天大学学报, 2000, 26(1): 5-7. LI Xiao-ming, LÜ Shan-wei, GAO Zhe-xi, et al. Finite- element analysis of temperature field of PCB and components[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(1): 5-7. |
| [2] | 赵健. PCB组件热-力分析的有限元模型及仿真[D]. 天津: 天津大学, 2006. ZHAO Jian. The finite element modeling and simulation for thermomechanical analysis of PCBA[D]. Tianjin: Tianjin University, 2006. |
| [3] | 杜平安, 刘建涛, 刘孝保. 电子器件振动特性有限元模型参数的等效计算[J]. 电子学报, 2010, 38(8): 1867-1873. DU Ping-an, LIU Jian-tao, LIU Xiao-bao. Equivalent computational methods of finite element model's parameters for vibration analysis of electronic module[J]. Acta Electronica Sinica, 2010, 38(8): 1867-1873. |
| [4] | AMY R A, AGLIETTI G S, RICHARDSON B G. Sensitivity analysis of simplified PCB finite element models[J]. Microelectronics Reliability, 2009, 49(7): 791- 799. |
| [5] | PITARRESI J M, CALETKA D V, CALDWELL R. The “smeared” property technique for the FE vibration analysis of printed circuit cards[J]. ASME Journal of Electronic Packaging, 1991, 113: 250-257. |
| [6] | PITARRESI J M, PRIMAVERA A A. Comparison of modeling techniques for the vibration analysis of printed circuit cards[J]. ASME Journal of Electronic Packaging, 1992, 114(4): 378-383. |
| [7] | 李春洋, 陈循, 陶俊勇, 等. 基于模态分析的印制电路板振动可靠性研究[J]. 中北大学学报(自然科学版), 2007, 28(2): 156-160. LI Chun-yang, CHEN Xun, TAO Jun-yong, et al. Study on printed circuit board reliability under vibration stress based on modal analysis[J]. Journal of North University of China(Natural Science Edition), 2007, 28(2): 156-160. |
| [8] | 刘孝保, 杜平安, 夏汉良, 等. 一种面向动态分析的PCB板等效建模方法[J]. 仪器仪表学报, 2011, 32(4): 863-869. LIU Xiao-bao, DU Ping-an, XIA Han-liang, et al. Dynamic property analysis-oriented PCB equivalent modeling method[J]. Chinese Journal of Scientific Instrument, 2011, 32(4): 863-869. |
| [9] | 倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1989. NI Zhen-hua. Vibration mechanics[M]. Xi'an: Xi'an Jiaotong University Press, 1989. |
| [10] | RAMTEKKAR G S, DESAI Y M, SHAH A H. Natural vibrations of laminated composite beams by using mixed finite element modeling[J]. Journal of Sound and Vibration, 2002, 257(4): 635-651. |
| [11] | VEL S S, BATRA R C. Three-dimensional exact solution for the vibration of functionally graded rectangular plates[J]. Journal of Sound and Vibration, 2004, 272(3-5): 703-730. |
 2015, Vol. 44
2015, Vol. 44
