CSVD在OFDM通信系统中的快衰落信道估计[1]、MIMO系统中的预编码[2]、信号处理[3]、图像处理[4]等领域中得到了广泛的应用。CSVD在工程中应用的关键在于数值计算,为了保证计算精度,通常会采用迭代运算的方法。文献[5]给出了一种直接复数双边Jacobi方法,该方法以一个复数 2x2为基本单元,并将其对角化,避免扩展矩阵维度。然而一个基本单元算法复杂,耗费的硬件资源较多,也需要多次迭代。文献[6]提出一种复转实的双边Jacobi方法,该方法将矩阵行列维度均扩大一倍,以一个实 2x2为基本单元,优点是基本单元简单,但是迭代次数增大,资源、延时和精度受限,实时性差,且这些算法对于长方矩阵具有明显的缺点。
本文提出了基于householder和双边Jacobi的混合优化算法,能有效地解决长方复矩阵奇异值分解的硬件实现和精度等问题。首先介绍了CSVD传统的算法即QR算法和双边Jacobi算法,并指出其对于处理长方阵的局限性。在此基础上提出一种混合优化算法,给出其具体运算步骤,并将该方法与现有常见算法性能比较,具体说明混合优化算法在硬件实现上的优势。最后以2x8复矩阵为例,给出了混合优化算法在FPGA上的实现及其测试结果。 1 复数矩阵奇异值分解
设$M$ 是一个 $m \times n$的复矩阵,如果存在一个分解有:
| $M = U \times S \times {V^H}$ | (1) |
式中,$U$是$m \times m$酉矩阵; $S$是半正定$m \times n$ 对角矩阵; $V$是 $n \times n$酉矩阵; ${V^{\rm{H}}}$为 的共轭转置。这样的分解就称为复矩阵$M$的奇异值分解。 $S$对角上的值为 $M$的奇异值。在工程实际中,只需要求得$V$矩阵即可。
1.1 传统长方阵CSVD算法目前传统复数长方阵的奇异值分解主要有两种较为常用:QR迭代算法和双边Jacobi算法。QR迭代算法首先采用householder变换将一般复矩阵化为二对角矩阵;然后采用Givens变换的方法交叉将非对角非零元素消零,如图 1所示,$S,T$分别代表行和列Givens矩阵,这一过程又称为“驱逐出境”;经过多次迭代将非对角化为零,最终达到收敛条件。
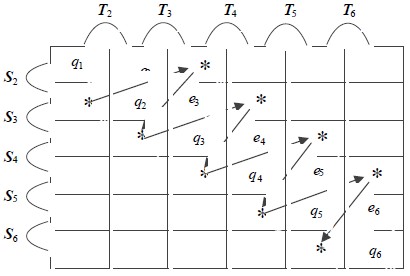 |
| 图 1 QR迭代“驱逐出境”示意图 |
双边Jacobi算法常见有:复转实双边Jacobi算法和直接复数双边Jacobi算法。两种算法的本质都是采用Brent-Luk-Van Loan(BLV)[7]脉动阵列迭代算法。所不同的是前者是将$n \times n$ 复矩阵转换为2$n \times 2n$ 的实矩阵,以 2x2矩阵为基本单元;而后者是直接对复2x2 矩阵进行对角化。
对于复转实算法,首先将一般复矩阵$M$ 转化为共轭对称矩阵$C$ ,即$C = {M^{\rm{H}}}M$ ,令$C = A + B{\rm{i}}$ ,$(u + {\rm{i}}v)$ 为$C$ 的奇异值$\sigma $所对应的奇异向量,则有:
| ${\rm{(}}A + {\rm{i}}B{\rm{)(}}u + {\rm{i}}v) = \sigma (u + {\rm{i}}v)$ | (2) |
| $\left[{\begin{array}{*{20}{c}} A&{ - B}\\ B&A \end{array}} \right]\left[{\begin{array}{*{20}{c}} u\\ v \end{array}} \right] = \sigma \left[{\begin{array}{*{20}{c}} u\\ v \end{array}} \right]$ | (3) |
对于直接复数双边Jacobi算法,以一个复数为基本运算单元进行对角化。其运算过程主要为以下两步:
| $\begin{array}{c} \left[{\begin{array}{*{20}{c}} {{\rm{cos}}\phi {{\rm{e}}^{{\rm{i}}{\theta _\alpha }}}}&{ - {\rm{sin}}\phi {{\rm{e}}^{{\rm{i}}{\theta _\beta }}}}\\ {{\rm{sin}}\phi {{\rm{e}}^{{\rm{i}}{\theta _\alpha }}}}&{{\rm{cos}}\phi {{\rm{e}}^{{\rm{i}}{\theta _\beta }}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{A_{11}}{{\rm{e}}^{{\rm{i}}{\theta _{11}}}}}&{{A_{12}}{{\rm{e}}^{{\rm{i}}{\theta _{12}}}}}\\ {{A_{21}}{{\rm{e}}^{{\rm{i}}{\theta _{21}}}}}&{{A_{22}}{{\rm{e}}^{{\rm{i}}{\theta _{22}}}}} \end{array}} \right] \times \\ \left[{\begin{array}{*{20}{c}} {{\rm{cos}}\varphi {{\rm{e}}^{{\rm{i}}{\theta _\gamma }}}}&{{\rm{sin}}\varphi {{\rm{e}}^{{\rm{i}}{\theta _\gamma }}}}\\ { - {\rm{sin}}\varphi {{\rm{e}}^{{\rm{i}}{\theta _\delta }}}}&{{\rm{cos}}\varphi {{\rm{e}}^{{\rm{i}}{\theta _\delta }}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {W{{\rm{e}}^{{\rm{i}}{\theta _w}}}}&{X{{\rm{e}}^{{\rm{i}}{\theta _x}}}}\\ 0&Z \end{array}} \right] \end{array}$ | (4) |
| $\begin{array}{c} \left[{\begin{array}{*{20}{c}} {{\rm{cos}}\lambda {{\rm{e}}^{{\rm{i}}{\theta _\xi }}}}&{ - {\rm{sin}}\lambda {{\rm{e}}^{{\rm{i}}{\theta _\eta }}}}\\ {{\rm{sin}}\lambda {{\rm{e}}^{{\rm{i}}{\theta _\xi }}}}&{{\rm{cos}}\lambda {{\rm{e}}^{{\rm{i}}{\theta _\eta }}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {W{{\rm{e}}^{{\rm{i}}{\theta _w}}}}&{X{{\rm{e}}^{{\rm{i}}{\theta _x}}}}\\ 0&Z \end{array}} \right] \times \\ \left[{\begin{array}{*{20}{c}} {{\rm{cos}}\rho {{\rm{e}}^{{\rm{i}}{\theta _\zeta }}}}&{{\rm{sin}}\rho {{\rm{e}}^{{\rm{i}}{\theta _\zeta }}}}\\ { - {\rm{sin}}\rho {{\rm{e}}^{{\rm{i}}{\theta _w}}}}&{{\rm{cos}}\rho {{\rm{e}}^{{\rm{i}}{\theta _w}}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} P&0\\ 0&Q \end{array}} \right] \end{array}$ | (5) |
这两种算法各有优缺点:QR迭代算法计算复杂度低,消耗更少的乘除法等硬件资源,但不稳定,当矩阵维度较大时,使得某次Givens矩阵为单位阵,“驱逐出境”会出现不收敛情况[8],导致QR算法失败;双边Jacobi[9]算法是基于脉动阵列结构的迭代算法,优点是结构简单对称,易于硬件实现,缺点是计算量比QR大,且精度与迭代次数相关。
针对上述两种算法的优缺点,本文提出一种混合优化算法,即混合householder和双边Jacobi的计算方法,优化了传统复数 2x2复数双边Jacobi的计算方法。
1.2 CSVD混合优化算法设$vec\_in = ({x_{\rm{1}}},{x_{\rm{2}}},\cdots ,{x_n})$ ,则该向量的householder变换[10, 11, 12]步骤如下:
1) 计算输入向量平方和得
| ${\sum ^{\rm{2}}}{\rm{ = }}x_1^2 + x_2^2 + \cdots + x_n^2$ | (6) |
| $\sigma = {\rm{sign(}}{x_{\rm{1}}}{\rm{)}} \times \sum ,{\rm{sign(}}{x_{\rm{1}}}{\rm{)}} = \frac{{{\rm{real(}}{x_{\rm{1}}}{\rm{)}} + {\rm{imag(}}{x_{\rm{1}}}{\rm{)i}}}}{{{\rm{abs(}}{x_{\rm{1}}}{\rm{)}}}}$ | (7) |
| $division\_factor = {\rm{2}}({\sum ^{\rm{2}}} + {\rm{abs(}}{x_{\rm{1}}}{\rm{)}} \times \sum )$ | (8) |
2) 构造行向量 ,并将其单位化得:
| $\begin{array}{l} u = vec\_in + \sigma {e_{{\rm{row}}}},{\rm{ }}{e_{{\rm{row}}}} = (0 \cdots 010 \cdots 0)\\ \uparrow {\rm{row}} \end{array}$ | (9) |
| ${u_e} = \frac{u}{{\left\| u \right\|}}$ | (10) |
3) 构造householder变换矩阵为:
| $H = I - {\rm{2}}{u_e}^{\rm{H}}{u_e} = I - {\rm{(2}}/{\rm{division\_factor)}}{u^{\rm{H}}}u$ | (11) |
4) 向量变换为:
| $vec\_out = vec\_in - u$ | (12) |
对于矩阵的householder变换,则需要逐行逐列调用向量householder变换,并在式(11)用变换矩阵$H$ 右乘,更新其他行向量。对于2x4$n$ 的复矩阵只需进行行变换,将一般矩阵化简为形如式(13)的二对角矩阵${M_k}$ ,并提取左上角非零复数2x2 矩阵$M$,则有:
| $\left[{\begin{array}{*{20}{c}} {{p_{\rm{1}}}}&{\rm{0}}& \cdots &{\rm{0}}\\ {{q_{\rm{1}}}}&{{q_{\rm{2}}}}& \cdots &{\rm{0}} \end{array}} \right]$ | (13) |
对$M$ 进行改进型复数双边Jacobi运算,其计算步骤如下:
1) 将复数2x2 矩阵转成共轭对称复矩阵:
| $M = \left[{\begin{array}{*{20}{c}} {{p_{\rm{1}}}}&{\rm{0}}\\ {{q_{\rm{1}}}}&{{q_{\rm{2}}}} \end{array}} \right]$ |
| ${M_{{\rm{sym}}}} = {M^{\rm{H}}}M = \left[{\begin{array}{*{20}{c}} A&{{b_r} + {b_i}i}\\ {{b_r} - {b_i}i}&D \end{array}} \right]$ | (14) |
2) 将${M_{{\rm{sym}}}}{\rm{(1,2)}}$ 转成幅角形式:
| $\left[{\begin{array}{*{20}{c}} A&{{b_r} + {b_i}i}\\ {{b_r} - {b_i}i}&D \end{array}} \right] = \left[{\begin{array}{*{20}{c}} A&{B{{\rm{e}}^{ - i{\theta _b}}}}\\ {B{{\rm{e}}^{ - i{\theta _b}}}}&D \end{array}} \right]$ | (15) |
3) 将复矩阵化为实矩阵:
| $\left[{\begin{array}{*{20}{c}} 1&0\\ 0&{{{\rm{e}}^{ - i{\theta _b}}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} A&{B{{\rm{e}}^{ - i{\theta _b}}}}\\ {B{{\rm{e}}^{ - i{\theta _b}}}}&D \end{array}} \right]\left[{\begin{array}{*{20}{c}} 1&0\\ 0&{{{\rm{e}}^{ - i{\theta _b}}}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} A&B\\ B&D \end{array}} \right]$ | (16) |
4) 计算双边Jacobi变换旋转角为:
| ${\rm{2}}\theta = {\rm{atan}}\left( {\frac{{{\rm{2}}B}}{{D - A}}} \right)$ | (17) |
5) 双边Jacobi变换为:
| ${\left[{\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{{\rm{sin}}\theta }\\ { - {\rm{sin}}\theta }&{{\rm{cos}}\theta } \end{array}} \right]^{\rm{T}}}\left[{\begin{array}{*{20}{c}} A&B\\ B&D \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{{\rm{sin}}\theta }\\ { - {\rm{sin}}\theta }&{{\rm{cos}}\theta } \end{array}} \right] = \left[{\begin{array}{*{20}{c}} P&0\\ 0&Q \end{array}} \right]$ | (18) |
6) $V$ 矩阵计算为:
| $V = \left[{\begin{array}{*{20}{c}} {\rm{1}}&{\rm{0}}\\ {\rm{0}}&{{{\rm{e}}^{ - i{\theta _b}}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{{\rm{sin}}\theta }\\ { - {\rm{sin}}\theta }&{{\rm{cos}}\theta } \end{array}} \right]$ | (19) |
2x8 CSVD的${V_{{\rm{svd}}}}$ 矩阵计算:将2x2 复数$V$ 矩阵补充到8x8 单位阵的1,2行列得到复酉矩阵${V_1}$ ,然后将householder产生的${H_1}$,${H_2}$ 与${V_1}$ 矩阵相乘即得到最终输出酉矩阵${V_{{\rm{svd}}}}$ ,即${V_{{\rm{svd}}}} = {H_{\rm{1}}} \times {H_{\rm{2}}} \times V$。
2 3种算法的比较与分析以2x4复矩阵为例,比较直接复数双边Jacobi(算法1),复转实双边Jacobi(算法2)和混合优化算法(算法3)在硬件资源消耗、迭代次数、误差精度之间的差异。
表 1给出了3种算法的性能比较,资源消耗为单次迭代次数下的运算量。图 2的精度比较结果是基于MATLAB中CORDIC函数浮点仿真结果。
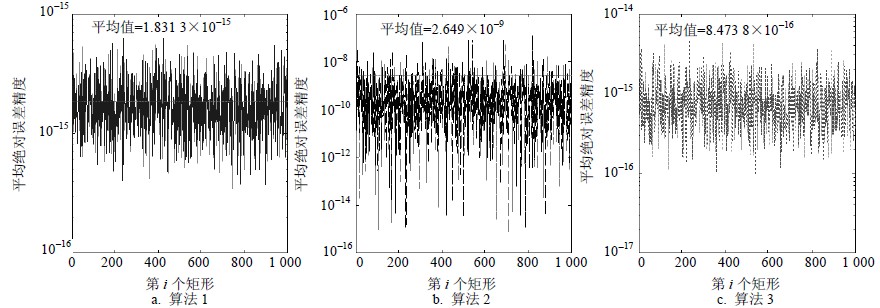 |
| 图 2 复矩阵2×4在3种算法下平均绝对误差精度比较 |
| 表 1 复矩阵2×4奇异值分解3种算法性能比较 |
更为一般地,对于$2 \times N $或$N \times 2 $的复长方矩阵,算法2和算法3的复杂度比较如图 3所示。
在图 3中将CORDIC单元、4个实数乘法统一等效为复数乘法。算法3中双边Jacobi运算在算法一基础上进行了优化,极大地减少硬件资源消耗。在单次迭代的情况下,算法2的资源消耗略低于算法3,通过硬件结构上的优化,可以使两种算法在资源消耗上相当。但是增加迭代次数即增加了处理延时,导致矩阵吞吐率(单位时间处理矩阵个数)急剧下降。且随着矩阵列数的增长,算法2和算法3之间的资源消耗差异将立方增长。
表 1中迭代次数并不固定,理论上可由BLV方法 总结公式得到,即${\rm{(lo}}{{\rm{g}}_{\rm{2}}}N + 1{\rm{)(}}N - 1{\rm{)}}$,而复转实的方法为${\rm{(lo}}{{\rm{g}}_{\rm{2}}}{\rm{(2}}N{\rm{)}} + 1{\rm{)(2}}N - 1{\rm{)}}$,$N$为复方阵阶数。
 |
| 图 3 算法2、算法3复杂度比较 |
计算误差的方法如下:设$M = US{V^{\rm{H}}}$,消去$U$,有$error = {M^{\rm{H}}}M - V{S^{\rm{H}}}S{V^{\rm{H}}}$,分别取误差矩阵$error$各元素的实部和虚部绝对值并取其平均。图 2中算法1和算法3精度高于算法2。误差的产生主要取决于CORDIC核,当增加迭代次数后,使得在对复数2 x 2对角化时非对角元素极小,此时${theta_b}$应作0或${\rm{\pi }}$处理。而CORDIC核仍求两极小数的比值来计算角度,进
而导致计算的角度${theta_b}$误差增大,最终导致输出$V$ 矩阵误差增大。特别是针对$2 \times 4n$ 的复矩阵,算法2需要先取其共轭转置并与其本身相乘,再扩展为维度为$8n \times 8n $的实矩阵,该矩阵至少包含$8n$个零元素。在迭代过程中容易产生极小的非对角元素。当然可以采取设置门限的方法,若非对角元素绝对值小于某一常数,直接置零。由此,对于奇异值分解的各种算法中迭代算法具有一定的不稳定性。
对于相同维度的长方复矩阵,算法3在资源和精度上要好于算法1和算法2,由于householder变换涉及乘、除、开方,且步骤并不像其他两种算法规则。算法3在实现的复杂度上要略高于其他两种算法。
3 2x8 CSVD的硬件实现结构CSVD的硬件实现主要包括两个模块:向量householder变换和改进型2 x 2复数双边Jacobi模块。这两个模块的计算是顺序的,因此可以设计为流水线结构。根据具体FPGA芯片资源的多少,可以灵活选择全流水或部分复用实现结构。
3.1 向量householder变换的实现结构一方面充分考虑资源的可复用程度,合理调配运算顺序;另一方面设计的结构应尽可能简单、模块化。图 4设计了一种全流水的行householder变换结构,对于大型矩阵可以复用该模块。
 |
| 图 4 行householder变换流水线硬件框图 |
本文提出的复数2x2双边Jacobi方法是在文献[5, 7]的基础上针对硬件结构提出的改进。文献[5, 7]方法对于一般复矩阵计算量偏大,特别是对于FPGA、DSP等硬件平台。但如果在对角化之前,先将复矩阵转换为共轭对阵矩阵,则计算量会大大减小。额外的资源消耗仅仅是2个复数2x2矩阵相乘。图 5的硬件框图相比于文献[5]的硬件框图更省资源。由于不用迭代运算,在精度上可以考虑减少乘法、CORDIC运算的位宽。如Xilinx平台下,一个实数乘法用18x25的位宽,可以保证最大化利用乘法器。其他运算以此为基准进行定点。图 5中CORDIC的3种模式均通过Xilinx的CORDIC IP核实现,本文将其设置为全并行模式,以保证整体流水线设计。
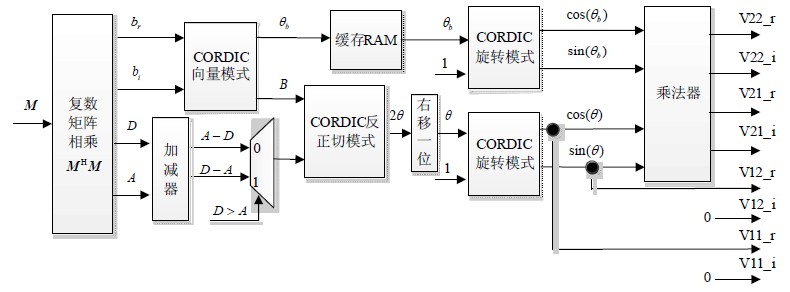 |
| 图 5 复数2×2对角化流水线硬件框图 |
对于输出$V$矩阵维度较大的复数奇异值分解,会耗费更多的FPGA资源如乘法器、除法器和CORDIC核。当DSP资源超过50%以后,布局布线后的最高时钟频率较综合后的最高时钟频率会大幅下降,主要原因在于乘法器核在布局布线过程中会产生较大的线延时,可通过减小乘法器输入输出的扇出解决,也可以通过更改综合工具设置。由布局布线后的结果才能比较准确反映设计的准确性和可靠性。本文设计采用Xilinx的FPGA硬件实现方案,其型号为xc6vlx240t-3ff1156,基本满足设计要求。表 2给出了算法2和算法3的资源占用比较,算法2实现平台为Altera Stratix IV。算法2为迭代结构,时钟频率为105 MHz,延时为3 800个时钟;而算法3为全并行,流水结构,布局布线后的最大时钟频率200.240 MHz,延时为330个时钟。算法3在资源和吞吐率上均优于算法2。
| 表 2复数2×8奇异值分解FPGA资源占用 |
本文提出了一种主要针对$2 \times 4n$或$4n \times 2$的CSVD混合优化算法,若矩阵维度为奇数,需要将矩阵维度向上扩充至偶数。该算法通过对多种传统算法的部分运算整合、改进,极大地减小了CORDIC核的使用且不需要迭代。通过与传统算法对比,该算法比传统算法至少在资源上节省26%,延时缩短10倍,精度提高一个数量级。最后对2x8CSVD进行FPGA实现,算法上的优势在硬件上得以体现。下一步将对更高维度的长方阵CSVD作探讨。
| [1] | AU E K S, JIN S, MCKAY M R, et al. Analytical performance of MIMO-SVD systems in ricean fading channels with channel estimation error and feedback delay[J]. IEEE Transactions on Wireless Communications, 2008, 7(4): 1315-1325. |
| [2] | SRINIVASAN J, RAJARAM S. FPGA implementation of precoding using low complexity SVD for MIMO-OFDM systems[C]//Information Communication and Embedded Systems (ICICES). [S.l.]: IEEE, 2013. |
| [3] | CHAKROBORTY S, SAHA G. Feature selection using singular value decomposition and QR factorization with column pivoting for text-independent speaker identification [J]. Speech Communication, 2010, 52(9): 693-709. |
| [4] | 胡谋法, 董文娟, 王书宏, 等. 奇异值分解带通滤波背景抑制和去噪[J]. 电子学报, 2008, 36(1): 111-116. HU Mou-fa, DONG Wen-juan, WANG Shu-hong, et al. Singular value decomposition band-pass-filter for image background suppression and denoising[J]. Acta Electronica Sinica, 2008, 36(1): 111-116. |
| [5] | WANG Y, CUNNINGHAM K, NAGVAJARA P, et al. Singular value decomposition hardware for MIMO: State of the art and custom design[C]//Reconfigurable Computing and FPGAs (ReConFig). [S.l.]: IEEE, 2010. |
| [6] | HAN Q, ZENG L. FPGA Implementation for low-rank channel estimation of OFDM[J]. Journal of Networks, 2012, 7(10): 1631-1638. |
| [7] | HEMKUMAR N D, CAVALLARO J R. A systolic VLSI architecture for complex SVD[C]//Circuits and Systems, ISCAS'92. [S.l.]: IEEE, 1992. |
| [8] | 赵学智, 叶邦彦. 单向收缩QR算法在奇异值分解中的收敛特性[J]. 电子科技大学学报, 2010, 39(5): 762-767.ZHAO Xue-zhi, YE Bang-yan. Convergence characteristic of single direction shrink QR algorithm in the singular value decomposition[J]. Journal of University of Electronic Science and Technology of China, 2010, 39(5): 762-767. |
| [9] | MA W, KAYE M E, LUKE D M, et al. An FPGA-based singular value decomposition processor[C]//Electrical and Computer Engineering. [S.l.]: IEEE, 2006. |
| [10] | LIU J, ZHANG J. A new maximum simplex volume method based on householder transformation for endmember extraction[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(1): 104-118. |
| [11] | PEDRAM A, GERSTLAUER A, GEIJN R A V D. Floating point architecture extensions for optimized matrix factorization[C]//Proceedings of the 2013 IEEE 21st Symposium on Computer Arithmetic. [S.l.]: IEEE, 2013: 49-58. |
| [12] | 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社有限公司, 2004. ZHANG Xian-da. Matrix analysis and applications[M]. Beijing: Tsinghua and Springer Publishing House, 2004. |
 2015, Vol. 44
2015, Vol. 44
