低密度奇偶校验(LDPC)码[1]是一种逼近香农限的好码,在深空通信、光通信和磁盘存储等众多领域得到广泛应用[2]。在其众多译码算法中,置信传播(belief-propagation,BP)[3]算法、归一化和偏移BP算法[4]性能优异,但实现复杂度较高。APP-Based(a posterioriprobability-based)算法和最小和(min-sum, MS)算法[3]是对BP算法的简化近似,文献[5, 6]提出的归一化APP-Based (normalized APP-based)、归一化最小和(normalized MS,NMS)与偏移最小和(offset MS,OMS)算法在性能和实现复杂度上得到一定的折中。比特翻转(bit flipping, BF)译码算法实现最为简单,适用于要求简单编译码装置的场合。加权BF(weighted BF, WBF)算法则将校验节点邻接的信息节点的最小幅度作为双极性校验子的权重[7]。文献[8]通过引入加权因子,使改进的WBF(modified WBF,MWBF)算法中的翻转函数更加有效。与MWBF算法相比,文献[9]提出的IMWBF(improved modified WBF)算法,取得了一定的增益。很多学者对上述WBF算法的结构进行修正,提出了一些改进的算法[10, 11, 12, 13, 14, 15]。对于上述WBF算法而言,信息节点和校验节点之间传递的仅仅是二进制信息(即校验式信息和翻转比特信息),属于二进制置信传播算法[16],实现复杂度大大降低。
文献[17]的IMWBF算法是基于归一化最小和(normalized MS-based,NMS-Based)算法的最优WBF算法,且WBF算法和MWBF算法是IMWBF算法的简化形式。但并没有对IMWBF算法翻转函数的物理意义做详细的分析说明,更没有从理论上得出如何简化IMWBF算法才能得出WBF算法和MWBF算法。本文从全新的角度出发,首先推导出IMWBF算法,得出其翻转函数中各项所代表的严格的物理意义;其次,根据这种全新的理解方式,推导得出MWBF算法和WBF算法,并阐明3种算法间的内在联系;最后提出一种可靠度外信息修正(extrinsic reliability adjustment,ERA)方案对WBF和MWBF算法进行改进。
1基本定义和算法描述码长为$N$、信息位长为$K$的二元LDPC码,可由$M$行$N$列的校验矩阵${\bf{H}} = [{h_{mn}}]$决定。对于规则LDPC码,${\bf{H}}$的第m行中1的数量用${d_r}$表示,第n列中1的数量用${d_c}$表示。${\bf{H}}$的第m行中1的位置可表示为${\bf{A}}(m){\rm{ = \{ }}n:{h_{mn}} = 1{\rm{\} }}$;第n列中1的位置可表示为${\bf{B}}(n){\rm{ = \{ }}m:{h_{mn}} = 1{\rm{\} }}$。
${\bf{c}} = \{ {c_n}\} _{n = 1}^N$为码字序列,经BPSK调制后得到$\tilde c{\rm{ = \{ }}2{c_n} - 1{\rm{\} }}_{n = 1}^N$。$\tilde c$进入加性高斯白噪声信道后得到接收序列${\kern 1pt} {\bf{y}} = \{ {y_n}\} _{i = 1}^N$,${y_n} = ({\rm{2}}{c_n} - {\rm{1}}) + {v_n}$,${v_n}$是均值为零、方差为${\sigma ^2}$高斯白噪声。${\bf{x}} = \{ {x_n}\} _{n = 1}^N$为硬判决输出序列,判决规则为\[{x_n} = [{\mathop{\rm sgn}} ({y_n}){\rm{ + }}1]/2\]。${\bf{E}} = \{ {e_n}\} _{n = 1}^N$表示错误图样,如果${x_n}$错误,则${e_n} = 1$;否则${e_n} = 0$。定义对数似然比为:
| ${L_n} = \ln \frac{{P({c_n} = 1|{y_n})}}{{P({c_n} = 0|{y_n})}} = \frac{4}{{{N_0}}}{y_n}$ | (1) |
伴随式为${\bf{S}} = \{ {s_m}\} _{m = 1}^M = {\bf{x}}{{\bf{H}}^{\rm{T}}}$,${\bar s_m} = 1 - {s_m}$为${s_m}$的补。${x_n}$参加的校验式集合可表示为${{\bf{s}}_{mn}} = \{ {s_m}{\rm{|}}m \in {\bf{B}}(n)\} $,被第m个校验方程校验的比特集合可记为${{\bf{X'}}_m} = \{ {x_n}|n \in {\bf{A}}(m)\} $,${x_n}$参加的校验集合所校验的所有比特记为${{\bf{X''}}_n} = \{ {x_n}|n \in {\bf{A}}(m),m \in {\bf{B}}(n)\} $。
1.1 MS-Based WBF算法的推导记比特${x_n}$发生错误的先验概率为qn,比特${x_n}$发生错误的后验概率为${\tilde q_n}$。则对于AWGN信道有[3, 18]: ${q_n} = {{\rm{e}}^{ - \left| {{L_n}} \right|}}/(1 + {{\rm{e}}^{ - \left| {{L_n}} \right|}})$。从而得到:$\ln [(1 - {q_n})/{q_n}] =$$\left| {{L_n}} \right| = \frac{4}{{{N_0}}}\left| {{y_n}} \right|$ 。由APP-Based算法可得[3]:
| $\begin{array}{c} \ln \left( {\frac{{{{\widetilde q}_n}}}{{1 - {{\widetilde q}_n}}}} \right){\rm{ = ln}}\left[ {\frac{{p({e_n} = 1{\rm{|}}{{\bf{s}}_{mn}},{\bf{y}})}}{{p({e_n} = 0{\rm{|}}{{\bf{s}}_{mn}},{\bf{y}})}}} \right] = \\ {\kern 1pt} \ln \left[ {\frac{{p({{\bf{s}}_{mn}}{\rm{|}}{e_n} = 1,{\bf{y}})}}{{p({{\bf{s}}_{mn}}{\rm{|}}{e_n} = 0,{\bf{y}})}}} \right] + \ln \left( {\frac{{{q_n}}}{{1 - {q_n}}}} \right){\kern 1pt} = \\ {\kern 1pt} \ln \left[ {\frac{{p({{\bf{s}}_{mn}}{\rm{|}}{e_n} = 1,{\bf{y}})}}{{p({{\bf{s}}_{mn}}{\rm{|}}{e_n} = 0,{\bf{y}})}}} \right] - \ln \left( {\frac{{1 - {q_n}}}{{{q_n}}}} \right){\kern 1pt} = \\ {\kern 1pt} \ln \left[ {\prod\limits_{m \in {\bf{B}}(n)} {\frac{{p({s_m}{\rm{|}}{e_n} = 1,{\bf{y}})}}{{p({s_m}{\rm{|}}{e_n} = 0,{\bf{y}})}}} } \right] - \ln \left( {\frac{{1 - {q_n}}}{{{q_n}}}} \right){\kern 1pt} = \end{array}$ |
| $\sum\limits_{m \in {\bf{B}}(n)} {\ln \left[ {\frac{{p({s_m}{\rm{|}}{e_n} = 1,{\bf{y}})}}{{p({s_m}{\rm{|}}{e_n} = 0,{\bf{y}})}}} \right]} - \ln \left( {\frac{{1 - {q_n}}}{{{q_n}}}} \right)$ | (2) |
| $\ln \left[ {\frac{{p({s_m}{\rm{|}}{e_n} = 1,{\bf{y}})}}{{p({s_m}{\rm{|}}{e_n} = 0,{\bf{y}})}}} \right] = \ln \left[ {{{\left( {\frac{{1 - {r_{mn}}}}{{{r_{mn}}}}} \right)}^{{s_m}}}{{\left( {\frac{{{r_{mn}}}}{{1 - {r_{mn}}}}} \right)}^{1 - {s_m}}}} \right] = $ |
| ${\kern 1pt} (2{s_m} - 1){\kern 1pt} \ln \left( {\frac{{1 - {r_{mn}}}}{{{r_{mn}}}}} \right)$ | (3) |
而
| ${r_{mn}} = \frac{1}{2}\left( {1 - \prod\limits_{i \in {\bf{A}}(m)\backslash n} {(1 - 2{q_i})} } \right)$ | (4) |
| $1 - {r_{mn}} = \frac{1}{2}\left( {1 + \prod\limits_{i \in {\bf{A}}(m)\backslash n} {(1 - 2{q_i})} } \right)$ |
式中,${r_{mn}}$为$\{ {x_i}|{{\bf{X'}}_m}\backslash {x_n}\} $中有奇数个错误的概率。利用近似关系[3]:
| $\prod\limits_{n \in {\bf{{\rm A}}}(m)} {(1 - 2{q_n})} \approx 1 - 2\mathop {\max }\limits_{n \in {\bf{A}}(m)} \{ {q_n}\} $ |
| ${r_{mn}} = \frac{{\exp \left( { - \frac{4}{{{N_0}}}\mathop {\min }\limits_{i \in {\bf{A}}(m)\backslash n} \{ \left| {{y_i}} \right|\} } \right)}}{{1 + \exp \left( { - \frac{4}{{{N_0}}}\mathop {\min }\limits_{i \in {\bf{A}}(m)\backslash n} \{ \left| {{y_i}} \right|\} } \right)}}$ | (5) |
从而有:
| $\ln \left( {\frac{{1 - {r_{mn}}}}{{{r_{mn}}}}} \right) \approx \frac{4}{{{N_0}}}\mathop {\min }\limits_{i \in {\bf{A}}(m)\backslash n} \{ \left| {{y_i}} \right|\} $ | (6) |
将式(6)代入式(3)得到:
| $\ln \left[ {\frac{{p({s_m}{\rm{|}}{e_n} = 1,{\bf{y}})}}{{p({s_m}{\rm{|}}{e_n} = 0,{\bf{y}})}}} \right] \approx \frac{4}{{{N_0}}}(2{s_m} - 1)\mathop {\min }\limits_{i \in {\bf{A}}(m)\backslash n} \{ \left| {{y_i}} \right|\} $ | (7) |
将式(7)代入式(2)得到:
| $\ln \left( {\frac{{{{\tilde q}_n}}}{{1 - {{\widetilde q}_n}}}} \right){\kern 1pt} = \frac{4}{{{N_0}}}(2{s_m} - 1)\sum\limits_{m \in {\bf{B}}(n)} {\mathop {\min }\limits_{i \in {\bf{A}}(m)\backslash n} \{ \left| {{y_i}} \right|\} } - \frac{4}{{{N_0}}}\left| {{y_n}} \right|$ | (8) |
式中,$\ln \left( {\frac{{{{\tilde q}_n}}}{{1 - {{\tilde q}_n}}}} \right)$为可靠度后验信息(posteriori reliabilityinformation, PRI);$\frac{4}{{{N_0}}}(2{s_m} - 1) \times $ $\sum\limits_{m \in {\bf{B}}(n)} {\mathop {\min }\limits_{i \in {\bf{A}}(m)\backslash n} \{ \left| {{y_i}} \right|\} } $为可靠度外信息(extrinsic reliability information,ERI);$\frac{4}{{{N_0}}}\left| {{y_n}} \right|$为可靠度内信息(intrinsicreliability information,IRI),即自身的可靠度先验信息。式(8)的物理意义可以解释为:1) 如果ERI>0,且$\left| {{\rm{ERI}}} \right|$越大,说明${x_n}$发生错误的概率越大;ERI<0,且$\left| {{\rm{ERI}}} \right|$越大,说明${x_n}$正确的概率越大。2) 如果IRI>0,IRI的值越大说明${x_n}$正确的概率越大。3) 如果ERI>IRI,即PRI>0,则说明${\tilde q_n} > 1 - {\tilde q_n}$,对${x_n}$翻转;否则,不翻转。常数项$4/{N_0}$并不影响译码性能,归一化处理后得到一种WBF算法,其翻转函数为:
| ${E_n}{\rm{ = }}\sum\limits_{m \in {\bf{B}}(n)} {(2{s_m} - 1)} {\omega _{mn}} - \left| {{y_n}} \right|$ | (9) |
式中,${\omega _{mn}}$为归一化ERI(normalized ERI,NERI)的幅度,${\omega _{mn}}{\rm{ = }}\mathop {\min }\limits_{i \in {\bf{{\rm A}}}(m)\backslash n} \{ \left| {{y_i}} \right|\} $,即为文献[16]中的MS-based WBF算法。$(2{s_m} - 1){\omega _{mn}}$为第m个校验方程提供的NERI,由${s_m}$和${\omega _{mn}}$决定;$\sum\limits_{m \in {\bf{B}}(n)} {(2{s_m} - 1){\omega _{mn}}} $校验方程提供的NERI,由${{\bf{s}}_{mn}}$和$\{ {x_i}|{{\bf{X''}}_n}\backslash {x_n}\} $决定;$\left| {{y_n}} \right|$为归一化IRI(NIRI),即${x_n}$的可靠度先验信息;${E_n}$为归一化PRI(NPRI)。
同时可以得出以下结论:1) 可以对满足$\{ {x_n}|n{\rm{ = }}$ $\arg {E_n} > 0\} $的比特都进行翻转,但性能并不理想[16]。MS-based WBF算法只对满足$\{ {x_n}|n{\rm{ = }}$ $\arg \mathop {\max }\limits_n {E_n}\} $比特翻转,即对发生错误后验概率最大的比特翻转。2) 文献[18]已证明利用Max-log MAP(MLP)算法译码的推导方式同样可以得到式(6)的结果,从而得到式(8)的结果。故MS-Based WBF算法是基于MLP准则的算法。
1.2 IMWBF算法的推导显然式(9)中的${\omega _{mn}}$也是MS算法中校验节点传递给信息节点的信息的幅度,考虑到${\omega _{mn}}$大于BP算法中校验节点传递给信息节点的信息的幅度[6],可对MS-Based WBF算法中的NERI进行归一化,便得到归一化MS-based WBF[18],其翻转函数为:
| ${E_n}{\rm{ = }}\alpha '\sum\limits_{m \in {\bf{B}}(n)} {(2{s_m} - 1){\omega _{mn}}} - \left| {{y_n}} \right|$ | (10) |
对式(10)进行变换后得到:
| ${E_n}{\rm{ = }}\sum\limits_{m \in {\bf{B}}(n)} {(2{s_m} - 1){\omega _{mn}}} - \alpha \left| {{y_n}} \right|$ | (11) |
式中,$\alpha $可以看做是$\alpha '$的倒数[16]。式(11)即是IMWBF算法的翻转函数,故IMWBF算法是基于归一化MLP(normalized MLP,NMLP)准则的算法[6]。式(11)中各项所代表的严格的物理意义与2.1节中定义的相同。
2 基于ERA方案的WBF算法 2.1 MWBF算法和WBF算法的推导如果对式(4)采用以下近似计算:
| ${r_{mn}} \approx \frac{1}{2}\left( {1 - \prod\limits_{n \in {\bf{{\rm A}}}(m)} {(1 - 2{q_n})} } \right)$ | (12) |
式(12)表示$\{ {x_n}|n \in {\bf{A}}(m)\} $中有奇数个错误的概率。将式(12)代入式(3)将有:
| $\ln \left[ {\frac{{p({s_m}{\rm{|}}{e_n} = 1,{\bf{y}})}}{{p({s_m}{\rm{|}}{e_n} = 0,{\bf{y}})}}} \right] \approx \frac{4}{{{N_0}}}(2{s_m} - 1)\mathop {\min }\limits_{n \in {\bf{A}}(m)} \{ \left| {{y_n}} \right|\} $ | (13) |
对式(13)做归一化处理,则可得到${x_n}$参加的第m个校验方程向其提供的NERI:$(2{s_m} - 1)\mathop {\min }\limits_{n \in {\bf{A}}(m)} \{ \left| {{y_n}} \right|\} $。同时考虑到NIRI便得到MWBF算法的翻转函数为:
| ${E_n}{\rm{ = }}\sum\limits_{m \in {\bf{B}}(n)} {(2{s_m} - 1){\omega _m}} - {\alpha _1}\left| {{y_n}} \right|$ | (14) |
式中,${\omega _m} = \mathop {\min }\limits_{n \in {\bf{{\rm A}}}(m)} \{ \left| {{y_n}} \right|\} $。如果不考虑${x_n}$的NIRI,即认为${x_n}$出错与正确先验等概,则式(14)变为:
| ${E_n}{\rm{ = }}\sum\limits_{m \in {\bf{B}}(n)} {(2{s_m} - 1){\omega _m}} - {\alpha _1}\left| {{y_n}} \right|$ | (14) |
| ${E_n}{\rm{ = }}\sum\limits_{m \in {\bf{B}}(n)} {(2{s_m} - 1){\omega _m}} $ |
由此得到文献[7]中的WBF算法。可见,通过对IMWBF算法的NERI进行近似可得到MWBF算法,WBF算法则是在MWBF算法的基础上,认为${x_n}$差错与否先验等概,因此二者在性能上必然会有不同程度的损失。
2.2 ERA方案相比于IMWBF算法,MWBF算法由于涉及式(12)的近似计算,从而引入某种相关性[5]。具体的,MWBF算法中第m个校验方程向$\{ {x_n}|n \in {\bf{A}}(m)\} $提供的NERI的幅度都为${\omega _m}$。然而$\{ {x_i}|{\kern 1pt} {\kern 1pt} i{\rm{ = }}\arg \mathop {\min }\limits_{i \in {\bf{A}}(m)} \{ \left| {{y_i}} \right|\} \} $得到的NERI幅度应该为序列$\{ \left| {{y_n}} \right|,n \in {\bf{A}}(m)\} $的次小值,即${x_i}$得到的外信息的可靠度降低,需要修正。传统意义上讲,要实现这种操作,首先要在${{\bf{X'}}_m}$中找到满足$\{ {x_i}|{\kern 1pt} {\kern 1pt} i{\rm{ = }}\arg \mathop {\min }\limits_{i \in {\bf{A}}(m)} \{ \left| {{y_i}} \right|\} \} $的信息节点,然后增加其可靠度[19]。显然传统方法是进行“先查找,后增加”的操作。由于WBF算法不涉及可靠度信息的更新传递,故增加校验方程中某个信息节点的可靠度等价于增加与其对应的${y_n}$的幅度,即可得到一种比传统实现方法更加简单的方法,具体步骤如下:
1) 对y的幅度进行预处理:
| $\left| {{\delta _n}} \right| \leftarrow \left| {{y_n}} \right|{\rm{ + }}\gamma $ | (15) |
2) 将序列$\{ \left| {{\delta _n}} \right|\} _{i = 1}^N{\kern 1pt} $和y共同送入译码器。
以下为基于ERA的MWBF译码算法步骤。
初始化:初始化迭代次数$k = 1$,设定最大迭代次数${K_{\max }}$。
1) 计算伴随式${\bf{S}}$,若${\bf{S}}$全为0,停止迭代,输出x;否则计算第m个校验方程的权重${\omega _m}{\rm{ = }}$ $\mathop {\min }\limits_{n \in {\bf{A}}(m)} \{ \left| {{\delta _n}} \right|\} ,m \in [1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} M]$。
2) 计算翻转函数为:
| ${E_n}{\rm{ = }}\sum\limits_{m \in {\bf{B}}(n)} {(2{s_m} - 1){\omega _m}} - {\alpha _2}\left| {{y_n}} \right|$ |
3) 比特翻转为:
| ${\kern 1pt} {x_n} = \bmod ({x_n} + 1,2)n{\rm{ = }}\arg \mathop {\max }\limits_n {E_n}$ |
4) 用更新过的x计算伴随式,如果${\bf{S}}$全零,则终止迭代;如果不为全零,但迭代次数达到最大次数限制,也终止迭代。否则$k{\rm{ = }}k{\rm{ + }}1$,跳至步骤2)。
由上述分析可知,新的实现方法只需进行“加法”的操作。需特别指出的是,传统实现方法最多只需增加$M$个信息节点的可靠度,而新的实现方案对校验方程中每个信息节点的可靠度都增加。而仿真结果表明,新的实现方案同样能有效地削弱近似计算带来的相关性,提高译码性能。为分析方便,认为1次比较运算等同于1次加法运算,则传统实现方法共需要$M({d_r} - 1)$次加法运算。同时,由式(15)可知,新的实现方案仅需要增加$N$次加法运算和$N$个存储单元。显然ERA方案可同时运用于WBF算法,而理论上得出最优化的修正因子$\gamma $仍然具有一定难度,可考虑通过仿真得到。
3 仿真结果和统计分析本节仿真参数如下:采用列重为3的(504,252) PEG-LDPC码(记为码A)和(1 008,504) PEG-LDPC码(记为码B)[14],迭代次数分别设定为50和100;在AWGN信道条件下,采用BPSK调制,在每个信噪比下至少采集1 000个比特错误。
3.1 寻找最佳的修正因子$\gamma $文献[8]通过蒙特卡洛仿真得出了MWBF算法的最优加权因子。类似地,文献[14]通过仿真得出了基于幅度和的WBF算法的最优加权因子。可见,当通过理论分析得到算法所需的最优因子较为困难时,蒙特卡洛仿真是首选的有效方法。由于目前通过理论分析得出修正因子$\gamma $较为困难,本文仍采用蒙特卡洛仿真。
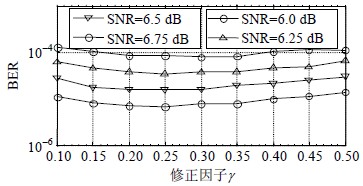 |
| 图 1 码A条件下,不同信噪比下$\gamma $对ERA-WBF算法性能的影响 |
图 1为不同信噪比下,ERA-WBF算法在码A条件下受不同$\gamma $影响时的误比特率性能。由图 1可知,对所有的Eb/N0可以选择一个固定不变且最优的$\gamma $,此时的性能损失可忽略不计,且保持较低的实现复杂度。6.0~6.5 dB时的最优化$\gamma $为0.3,而6.75 dB时最优化的$\gamma $为0.25,但考虑到6.75 dB时$\gamma $=0.25和$\gamma $=0.3时性能损失可忽略不计,故本文仿真中ERA-WBF算法在码A条件下最优化的$\gamma $设定为0.3。
3.2 算法性能和实现复杂度比较图 2为最优参数下,码A和码B在各算法下性能比较。MWBF算法的最优加权系数分别设定为0.2和0.3[14],IMWBF算法的最优加权系数都设定为0.2[9],ERA-WBF的最优$\gamma $分别设定为0.3和0.2,ERA-MW- BF的最优$\gamma $都设定为0.45。图 3给出码B在各译码算法下平均迭代次数比较。图 4给出码A在IMWBF和MS-Based WBF算法下误比特性能。
 |
| 图 2 码A和码B在各译码算法下性能比较 |
 |
| 图 3 码B在各算法下平均迭代次数统计 |
 |
| 图 4 码A在IMWBF和MS-Based WBF算法下性能图 |
表 1给出BER=10-5时,各算法的性能比较。由表 1可知,在码A条件下,ERA-MWBF算法与IMWBF算法的性能基本一致。在BER=10-5时,相对于MWBF算法,ERA-MWBF算法可获得0.45 dB的增益;ERA-WBF算法相对于WBF算法可获得0.30dB的增益。在码B条件下,当Eb/N0大于4.25 dB时,ERA-MWBF的性能甚至好于IMWBF算法。在Eb/N0大于5.0 dB时,ERA-WBF算法的性能也要好于MWBF算法。从图 3可知,修正后WBF算法和MWBF算法的平均迭代次数大大降低。为分析方便,认为一次比较运算等同于一次加法运算。当Eb/N0=4.5 dB时,由图 3得出,ERA-MWBF算法的平均迭代次数比传统算法降低20次,加法运算次数平均降低$20(N - 1 + {d_c}{d_r}) = 20{\kern 1pt} {\kern 1pt} {\kern 1pt} 520$次[14],总体上平均加法运算次数降低了$20{\kern 1pt} {\kern 1pt} {\kern 1pt} 520 - N = 19{\kern 1pt} {\kern 1pt} {\kern 1pt} 512$次。类似的,Eb/N0=4.0 dB和5.0 dB时,总体上平均加法运算次数都减低14382次。从图 4可知,IMWBF和MS-BasedWBF算法分别是基于NMLP准则和MLP准则得出的,因此前者性能必然优于后者。
| 表 1 BER=10-5,各算法在码A和码B下性能统计 |
本文从一个新的角度得出IMWBF算法的物理意义,分析了IMWBF算法与WBF算法和MWBF算法的内在联系。以此为基础提出一种ERA方案对WBF算法和MWBF算法进行改进。仿真结果表明,AWGN信道下,误比特率为10-5时,与传统算法相比,基于ERA方案的WBF和MWBF算法可分别获得约0.70 dB和0.76dB的增益,同时实现复杂度有所降低,从而在纠错性能和实现复杂度之间达到了很好的平衡匹配。文献[7, 8, 9, 10, 11, 12, 13, 14, 15]和本文提出的改进方案都以单比特翻转模式为出发点,即每次迭代过程中对发生错误概率最大的比特执行翻转操作,隶属于串行算法。多比特翻转模式下的算法仍有待深入研究。此外,本文提出的改进方案适用于行重和列重相对较小的LDPC码。仿真结果表明,此改进方案对于行重和列重较大的LDPC码则不太适用。针对行重和列重较大的LDPC码,多比特翻转模式下的改进方案值得进一步的深入研究。
| [1] | GALLAGER R G. Low density parity check codes[J]. IEEE Transactions on Information Theory, 1962, 8(1): 21-28. |
| [2] | 施玉晨, 白宝明. 基于多元LDPC码的多用户协作方案[J]. 电子科技大学学报, 2013, 42(8): 205-208.SHI Yu-chen, BAI Bao-ming. Multiuser cooperative scheme based on nonbinary LDPC codes[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(8): 205-208. |
| [3] | FOSSORIER M, MIHALJEVIC M, IMAI H. Reduced complexity iterative decoding low density parity-check codes based on belief propagation[J]. IEEE Transactions on Information Theory, 1999, 47(5): 673-680. |
| [4] | YAZDANI M, HEMATI S, BANIHASHEMI A. Improving belief propagation on graphs with cycles[J]. IEEE Communications Letters, 2004, 8(1): 57-59. |
| [5] | CHEN Jing-hu, FOSSORIER M. Decoding low-density parity check codes with normalized APP-based Algorithm[C]//Global Telecommunication Conference. San Antonio, TX, USA: IEEE, 2001(2): 1026-1030. |
| [6] | CHEN Jing-hu, DHOLAKIA A, ELEFTHERIOU E, et al. Reduced-complexity decoding of LDPC codes[J]. IEEE Transactions on Communications, 2005, 53(8): 1288-1299. |
| [7] | KOU Y, LIN Shu, FOSSORIER M. Low-density parity-check codes based on finite geometries: a rediscovery and new results[J]. IEEE Transactions on Information Theory, 2001, 47(7): 2711-2736. |
| [8] | ZHANG Jun-tan, FOSSORIER M. A modified weighted bit-flipping decoding of low-density parity-check codes[J]. IEEE Communications Letters, 2004, 8(3): 165-167. |
| [9] | JIANG Ming, ZHAO Chun-ming, SHI Zhi-hua, et al. An improvement on the modified weighted bit flipping decoding algorithm for LDPC codes[J]. IEEE Communications Letters, 2005, 9(9): 814-816. |
| [10] | GUO F, HANZO L. Reliability ratio based weighted bit-flipping decoding for low-density parity-check codes[J]. Electronics Letters, 2004, 40(21): 1356-1358. |
| [11] | 刘原华, 张美玲. LDPC码的改进迭代比特翻转译码算法[J]. 电讯技术, 2012, 52(4): 488-491. LIU Yuan-hua, ZHANG Mei-ling. An improved iterative bit-flipping decoding algorithm for low-density parity-check codes[J]. Telecommunications Engineering, 2012, 52(4): 488-491. |
| [12] | CHEN T. An efficient bit-flipping decoding algorithm for LDPC codes[C]//International Conference on Cross Strait Quad-Regional Radio Science and Wireless Technology. New Taipei City, Taiwan, China: IEEE, 2012: 109-112. |
| [13] | 刘原华, 张美玲. 结构化LDPC码的改进比特翻转译码 算法[J]. 北京邮电大学学报, 2012, 35(4): 116-119. LIU Yuan-hua, ZHANG Mei-ling. Improved bit-flipping method for decoding structured low-density parity-check codes[J]. Journal of Beijing University of Posts and Telecommunications, 2012, 35(4): 116-119. |
| [14] | 张高远, 周亮, 苏伟伟,等. 基于平均幅度的LDPC码加 权比特翻转译码算法[J]. 电子与信息学报, 2013, 35(11): 2572-2578. ZHANG Gao-yuan, ZHOU Liang, SU Wei-wei, et al. Average magnitude based weighted bit-flipping decoding algorithm for LDPC codes[J]. Journal of Electronics & Information Technology, 2013, 35(11): 2572-2578. |
| [15] | CHEN T. Channel-independent weighted bit-flipping decoding algorithm for low-density parity-check codes[J]. IET Communications, 2012, 6(17): 2968-2973. |
| [16] | NASTARAN M. New iterative decoding algorithms for low-density parity-check (LDPC) codes[D]. Ottawa, Canada: Carleton University, 2011. |
| [17] | WU Xiao-fu, LING C, JING Ming, et al. New insights into weighted bit-flipping decoding[J]. IEEE Transactions on Communications, 2009, 57(8): 2177-2181. |
| [18] | 张立军, 刘明华, 卢萌. 低密度奇偶校验码加权大数逻 辑译码研究[J]. 西安交通大学学报, 2013, 47(4): 35-38. ZHANG Li-jun, LIU Ming-hua, LU Meng. A research on weighted majority-logic decoding for LDPC codes[J]. Journal of Xi’an Jiaotong University, 2013, 47(4): 35-38. |
| [19] | DARABIHA A, CARUSONE A C, KSCHISCHANG F R. A bit-serial approximate min-sum LDPC decoder and FPGA implementation[C]//IEEE International Symposium on Circuits and Systems. Island of Kos, Greece: IEEE, 2006: 149-152. |
 2015, Vol. 44
2015, Vol. 44
