无网格方法是继网格方法之后出现的一种新型数值方法。计算区域的离散只涉及布点填充,既可以采用网格点,也可以打破传统的网格方法[1]中网格拓扑的约束而根据需要直接布点,因此,该方法在对复杂外形的处理上更加灵活[2]。近年来,无网格方法已在计算电磁学(computational electromagnetics, CEM)领域得到了应用和发展,用于求解电磁场问题的代表性方法有局部弱式Petrov-Galerkin无网格法和径向基点插值无网格法等[3, 4, 5]。这些方法通常会涉及形函数(或基函数)的选取。形函数的选择不仅会影响矩阵的质量[6],还会影响到边界条件的施加,有时边界条件需要采用特殊的方法强制给定[7]。在计算流体力学(computational fluid dynamics, CFD)领域,近年来也出现了与CEM中做法不同的无网格方法。无网格点上的空间导数可基于局部点云结构通过极小曲面逼近得到。空间离散涉及的通量运算常采用近似黎曼解处理。该类无网格方法已成功应用于求解Euler方程,能模拟出复杂外形的绕流[2]。
鉴于所研究的麦克斯韦方程和流体力学中的Euler方程具有双曲型等相同的数学特性,本文意在借鉴上述CFD中的无网格算法,发展基于加权本质无振荡(weighted essentiallynon-oscillatory, WENO)重构的时域无网格算法,用于求解麦克斯韦方程。CFD中的WENO重构是在本质无振荡(essentiallynon-oscillatory,ENO)重构方法[8]的基础上发展而来的高阶重构方法,大多用于结构网格[9]。本文基于无网格点云和局部一维坐标,给出了WENO重构实施所要求模板的构造方法。通量运算涉及的无网格点云中心点与卫星点连线中点处物理量的左右状态值,改用三阶WENO重构计算,以替代通常的线性重构。空间离散涉及的通量运算采用基于点云结构的近似黎曼解方法确定,时间离散则按照四步Runge-Kutta法推进求解。然后结合算例分析,验证了本文基于WENO重构的数值解比通常的线性重构结果更接近理论解。最后,本文研究了双NACA0012翼型及飞机投弹模拟的多体干扰电磁散射特性,在一定程度上展示了算法处理多体干扰等复杂情形的能力。
1 时域麦克斯韦方程对于横磁(transversemagnetic, TM)波,在直角坐标系中守恒型无量纲时域麦克斯韦方程可写为:
| $\frac{{\partial W}}{{\partial t}} + \left( {\frac{{\partial {F_1}}}{{\partial x}} + \frac{{\partial {F_2}}}{{\partial y}}} \right) = S$ | (1) |
式中,$W = \left[ {\begin{array}{*{20}{c}} {\varepsilon {E_z}}\\ {\mu {H_x}}\\ {\mu {H_y}} \end{array}} \right]$;${F_1} = \left[ {\begin{array}{*{20}{c}} { - {H_y}}\\ 0\\ { - {E_z}} \end{array}} \right]$;${F_2} = \left[ {\begin{array}{*{20}{c}} {{H_x}}\\ {{E_z}}\\ 0 \end{array}} \right]$;$S = \left[ {\begin{array}{*{20}{c}} { - \sigma {E_z}}\\ { - {\sigma _m}{H_x}}\\ { - {\sigma _m}{H_y}} \end{array}} \right]$;${H_x}$和${H_y}$分别为磁场强度$H$在$x$和$y$方向上的分量;${E_z}$为电场强度$E$在z方向上的分量;$\varepsilon $为介电常数;$\sigma $为电导率;$\mu $为磁导率;${\sigma _m}$为磁阻率。
2 时域麦克斯韦方程的无网格离散求解 2.1 计算区域布点离散及点云生成无网格算法计算区域的离散只涉及布点填充,既可以方便地选取结构网格或非结构网格点,也可以打破传统的网格拓扑约束,按要求直接布点。计算区域布点填充后,在点的局部需构成无网格算法实施所要求的点云结构。以点云${C_i}$为例,如图 1所示,中心点$i$自然纳入点云${C_i}$中,再合理选取一定数目的卫星点。本文以中心点$i$为圆心,${r_i}$为半径画圆,将圆内除中心点$i$以外的点(1、2、3、4、5和6)视为卫星点一并纳入点云${C_i}$中。其中圆半径${r_i}$与点云当地点与点之间的距离相关,通常可通过扩大或缩小${r_i}$来选取合适数目的卫星点。
 |
| 图 1 无网格点云${C_i}$示意图 |
2.2 空间导数逼近
当点云生成后,在点云${C_i}$上假定中心点$i$附近的函数值分布满足函数$f = f(x,y)$。那么,沿用文献[10]的方法,$f$的二次逼近函数可写为:
| $\bar f = {f_i} + {a_1}h + {a_2}l + 0.5{a_3}h_{}^2 + 0.5{a_4}l_{}^2 + {a_5}{h_{}}{l_{}}$ | (2) |
式中,${f_i} = f({x_i},{y_i})$;$h = x - {x_i}$;$l = y - {y_i}$;${a_i}(i = 1,2, \cdots ,5)$为待定系数,表示在中心点$i$处相应的各阶偏导数。在点云${C_i}$上,记卫星点$k$$(k = 1,2, \cdots ,M)$处的函数值为${f_k}$,则定义函数逼近的总体误差为:
| $G = \frac{1}{2}\sum\limits_{k = 1}^M {{{({f_k} - {{\bar f}_k})}^2}} $ | (3) |
基于总体误差$G$极小,逼近函数可整理为[10]:
| $f(x,y) = {f_i} + \sum {{\alpha _k}({f_k} - {f_i})h} + \sum {{\beta _k}({f_k} - {f_i})l} + $ |
| $0.5\sum {{\gamma _k}({f_k} - {f_i})} {h^2} + 0.5\sum {{\eta _k}({f_k} - {f_i})} {l^2} + $ |
| $\sum {{\zeta _k}({f_k} - {f_i})h} l$ | (4) |
式中,系数${\alpha _k}$、${\beta _k}$、${\gamma _k}$、${\eta _k}$和${\zeta _k}$仅与离散点的坐标相关,可在迭代计算前一次计算得到。函数$f$在中心点$i$处的空间导数${a_i}(i = 1,2, \cdots ,5)$可表示为:
| ${a_1} = \sum {{\alpha _k}({f_k} - {f_i})}$, ${a_2} = \sum {{\beta _k}({f_k} - {f_i})} $ |
| ${a_3} = \sum {{\gamma _k}({f_k} - {f_i})}$, ${a_4} = \sum {{\eta _k}({f_k} - {f_i})} $ |
| ${a_5} = \sum {{\zeta _k}({f_k} - {f_i})} $ | (5) |
同样地,也可以用中心点与卫星点连线中点$ik$处的函数值${f_{ik}}$进行表示:
| ${a_1} = \sum {{\alpha _{ik}}({f_{ik}} - {f_i})}$,${a_2} = \sum {{\beta _{ik}}({f_{ik}} - {f_i})} $ |
| ${a_3} = \sum {{\gamma _{ik}}({f_{ik}} - {f_i})} $,${a_4} = \sum {{\eta _{ik}}({f_{ik}} - {f_i})} $ |
| ${a_5} = \sum {{\zeta _{ik}}({f_{ik}} - {f_i})} $ | (6) |
式中,整理得到的系数${\alpha _ik}$、${\beta _ik}$、${\gamma _ik}$、${\eta _ik}$和${\zeta _ik}$也仅与离散点的坐标相关,可在迭代计算前一次计算得到。本文将根据式(6)处理下面空间离散涉及的通量运算。
2.3 基于无网格点云的WENO重构为了提高时域无网格算法的计算精度,本文借鉴CFD中三阶WENO重构的有限差分方法[11]构造在点云中实施WENO重构所要求的模板。为此,基于点云结构,在点云${C_i}$上以中心点$i$和卫星点$k$为例,建立局部一维坐标,如图 2所示。图中点$ii$是点$i$关于点$k$的对称点(虚拟点),点$kk$是点$k$关于点$i$的对称点。记点$i$和点$k$处的函数值分别为${f_i}$和${f_k}$,虚拟点$ii$和$kk$处的函数值分别记为${f_ii}$和${f_kk}$,则点$i$和点$k$的中点$ik$处的函数值${f_Lik}$和${f_Rik}$可按照下式WENO重构进行计算:
 |
| 图 2 基于无网格点云的WENO重构模板示意图 |
| $\left\{ \begin{array}{l} {f_{Lik}} = {\xi _1}( - 0.5{f_{kk}} + 1.5{f_i}) + {\xi _2}(0.5{f_i} + 0.5{f_k})\\ {f_{Rik}} = {\xi _1}( - 0.5{f_{ii}} + 1.5{f_k}) + {\xi _2}(0.5{f_k} + 0.5{f_i}) \end{array} \right.$ | (7) |
式中,加权因子${\xi _1} = 1/3$;${\xi _2} = 2/3$。于是式(7)可进一步整理为:
| $\left\{ \begin{array}{l} {f_{Lik}} = ( - {f_{kk}} + 5{f_i} + 2{f_k})/6\\ {f_{Rik}} = ( - {f_{ii}} + 5{f_k} + 2{f_i})/6 \end{array} \right.$ | (8) |
只要虚拟点上的函数值${f_ii}$和${f_kk}$能够计算得到,就可按照式(8)WENO重构计算出中点$ik$处的函数值${f_Lik}$和${f_Rik}$,以备进行通量运算。
对于虚拟点上的函数值,最直接的做法是针对虚拟点,逐一选点并构造插值模板,再按照插值方法确定。但是,要逐一搜索插值点,且在计算插值系数的过程中还会涉及矩阵求逆,都需要花费较多的计算时间。为了减小不必要的计算量,本文利用已知的离虚拟点最近的点云结构及其空间导数信息,通过采用形如式(4)的二次函数逼近来插值计算出虚拟点上的函数值。
2.4 通量运算在${C_i}$上,应用式(6)近似中心点$i$处的通量为:
| $\begin{array}{c} {\left. {\left( {\frac{{\partial {F_1}}}{{\partial x}} + \frac{{\partial {F_2}}}{{\partial y}}} \right)} \right|_i} = \sum {{\alpha _{ik}}({F_1}_{ik} - {F_1}_i)} + \\ \sum {{\beta _{ik}}({F_2}_{ik} - {F_2}_i)} = \end{array}$ |
| $\sum {({\alpha _{ik}}{F_1}_{ik} + {\beta _{ik}}{F_2}_{ik})} - \sum {({\alpha _{ik}}{F_1}_i + {\beta _{ik}}{F_2}_i)} $ | (9) |
式中,$\sum {({\alpha _{ik}}{F_1}_i + {\beta _{ik}}{F_2}_i)} $仅与点云中心点处的计算值相关,因此,迭代计算时此项如同已知项可直接利用当前计算点的值计算确定;而$\sum {({\alpha _{ik}}{F_1}_{ik} + } $ ${\beta _{ik}}{F_2}_{ik})$要用到点云中心点$i$与卫星点$k$连线中点处的值,为此,定义数值通量为:
| ${Q_{ik}} = {m_{ik}}{F_{1ik}} + {n_{ik}}{F_{2ik}}$ | (10) |
式中,${m_{ik}} = {\alpha _{ik}}/\sqrt {\alpha _{ik}^2 + \beta _{ik}^2} $;${n_{ik}} = {\beta _{ik}}/\sqrt {\alpha _{ik}^2 + \beta _{ik}^2} $。定义矢量${d_{ik}} = ({\alpha _{ik}},{\beta _{ik}})$,则式(9)可简写为:
| ${\left. {\left( {\frac{{\partial {F_1}}}{{\partial x}} + \frac{{\partial {F_2}}}{{\partial y}}} \right)} \right|_i} = \sum\limits_{k = 1}^M {{Q_{ik}}\left| {{d_{ik}}} \right|} - \sum\limits_{k = 1}^M {({\alpha _{ik}}{F_1}_i + {\beta _{ik}}{F_2}_i)} $ | (11) |
再采用近似黎曼解确定数值通量${Q_{ik}}$,即:
| ${Q_{ik}} = \left[ {\begin{array}{*{20}{c}} { - {{\hat d}_{ik}}{H_{ik}}}\\ {{{\hat d}_{ik}}{E_{ik}}} \end{array}} \right] = $ |
| $\left[ {\begin{array}{*{20}{c}} { - {{\hat d}_{ik}}\frac{{{{(\mu c)}_L}{H_L} + {{(\mu c)}_R}{H_R} - {{\hat d}_{ik}}({E_R} - {E_L})}}{{{{(\mu c)}_L} + {{(\mu c)}_R}}}}\\ {{{\hat d}_{ik}}\frac{{{{(\varepsilon c)}_L}{E_L} + {{(\varepsilon c)}_R}{E_R} + {{\hat d}_{ik}}({H_R} - {H_L})}}{{{{(\varepsilon c)}_L} + {{(\varepsilon c)}_R}}}} \end{array}} \right]$ |
式中,${\hat d_{ik}} = ({m_{ik}},{n_{ik}})$是${d_{ik}}$的单位矢量;${H_L}$、${E_L}$、${H_R}$和${E_R}$均按本文WENO重构进行计算。
2.5 时间离散采用无网格方法对麦克斯韦方程进行空间离散后,在点云${C_i}$上,可以得到其半离散形式为:
| ${\left. {\frac{{\partial W}}{{\partial t}}} \right|_i} = - \sum\limits_{k = 1}^M {{Q_{ik}}\left| {{d_{ik}}} \right| + \sum\limits_{k = 1}^M {({\alpha _{ik}}{F_1}_i + {\beta _{ik}}{F_2}_i)} + {{\left. S \right|}_i}} \equiv - {R_i}$ | (13) |
式中,${R_i}$为点云中心点,即计算点上的残差。本文利用式(13)按照4步Runge-Kutta格式[10]进行时间推进求解。迭代计算时,如式(9)~式(12)所示,残差计算涉及的各空间离散项则利用当前计算值计算确定。对于计算涉及的边界条件,本文在物面应用良导体边界条件,而在计算域的截断位置则采用完全匹配层边界条件,具体公式及参数取值详见文献[10]。
3 算例与分析$x$、$y$坐标均为以入射波波长$\lambda $为特征长度、无量纲化后的空间位置。如图 3所示,TM平面波沿$k$方向照射目标,并定义$k$轴与$x$轴之间的夹角为入射角$\varphi $,那么归一化后的入射波分量可表示为:
| $\left\{ \begin{array}{l} E_z^i = \cos [2\pi (k - t)]\\ H_x^i = \sin \varphi \times \cos [2\pi (k - t)]\\ H_y^i = - \cos \varphi \times \cos [2\pi (k - t)] \end{array} \right.$ | (14) |
式中,$k = x\cos \varphi + y\sin \varphi $;$t$为无量纲参数。
 |
| 图 3 TM平面波 |
3.1 一维电磁波传播数值模拟
本文先选用具有解析解的一维电磁波传播问题对发展的WENO重构算法进行考核。假定电磁波沿$x$方向传播,那么式(1)的麦克斯韦方程可简化为:
| $\frac{{\partial {W_{1D}}}}{{\partial t}} + \frac{{\partial {F_{1D}}}}{{\partial x}} = 0$ | (15) |
式中,${W_{1D}} = \left[ {\begin{array}{*{20}{c}} {\varepsilon {E_z}}\\ {\mu {H_y}} \end{array}} \right]$;${F_{1D}} = \left[ {\begin{array}{*{20}{c}} { - {H_y}}\\ { - {E_z}} \end{array}} \right]$。数值模拟时采用周期性边界条件,计算域取从$x = - 5\lambda $至$x = 5\lambda $,初场设置为:
| ${E_z}\left| {_{t = 0}} \right. = \cos 2{\rm{\pi }}x$,${H_y}\left| {_{t = 0}} \right. = - \cos 2{\rm{\pi }}x$ | (16) |
对应的解析解为:
| ${E_{z,{\rm{th}}}} = \cos [2\pi (x - t)]$,${H_{y,{\rm{th}}}} = - \cos [2\pi (x - t)]$ | (17) |
在$t = 10$时刻提取相应的电场信息进行研究。定义计算误差为:
| ${\rm{error}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{({E_{z,{\rm{cal}}}} - {E_{z,{\rm{th}}}})}^2}} } $ | (18) |
式中,${E_{z,{\rm{cal}}}}$为计算值。
图 4给出了计算误差与布点密度的关系。整体上看,不论基于WENO重构还是线性重构,${\rm{error}}$随${\rm{dom}}$的增加而减小;${\rm{dom}}$一定时,本文数值解的${\rm{error}}$显著小于线性重构的结果,计算得到的电场幅值和相位均与理论解更加接近。
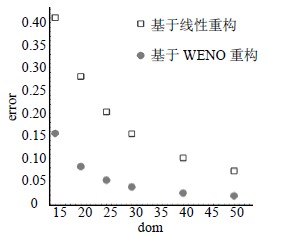 |
| 图 4 计算误差与布点密度的关系 |
本文选用有级数解[12]可供比较的金属圆柱算例进行电磁散射模拟。先采用如图 5a所示的均匀布点方式,布点密度${\rm{dom}} = 20$。数值模拟时,圆柱半径为$2.0\lambda $,计算域设置为$12\lambda \times 12\lambda $,总点数为60 698,TM波入射角$\varphi = 0^\circ $。计算得到的圆柱散射场和双站雷达散射截面(radar cross section, RCS)分布分别如图 6和图 7所示,图 7给出了级数解比较。从图 7不难看出,本文基于WENO重构计算得到的双站RCS和传统基于线性重构的计算结果,其峰值及其在整个双站角范围内的分布整体上都能与级数解一致;但是在各极值点处,本文结果与级数解吻合更好,如图 7b所示。
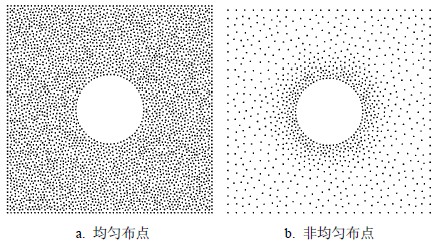 |
| 图 5 圆柱计算点云示意图 |
 |
| 图 6 圆柱的散射场等值线分布 |
 |
| 图 7 圆柱的双站RCS分布及局部放大图 |
本例均匀布点方式离散计算区域总点数达60 698,计算量较大。考虑到本文在物面处引入入射波及提取时域信息,因此物面附近的布点密度应予以保证,而对于截断边界附近,布点密度适当放宽。改用如图 5b所示的非均匀布点方式重新计算圆柱散射场,其他条件设置同图 5a,计算得到的双站RCS分布如图 8所示。从图中不难看出,当${\rm{dom}} = 10$时,计算得到的双站RCS分布与均匀布点的结果基本吻合;当${\rm{dom}} = 8$时,除个别极值点处数值有差异外,计算值大体上也能与均匀布点情形一致;当${\rm{dom}} = 5$时,计算值与均匀布点的结果存在明显差异,如图 8b所示。当${\rm{dom}} = 10$时,总点数由均匀布点的60 698下降到16 380,计算量显著减小,而计算结果几乎不受影响。
 |
| 图 8 不同布点密度对应的圆柱双站RCS分布及局部放大图 |
选用双NACA0012翼型算例[13]验证本文算法处理多体干扰问题的能力。沿用文献[13]的做法,取NACA0012翼型弦长为$4\lambda $,双翼型弦线之间的距离为$\lambda $。计算域取$12\lambda \times 12\lambda $,电磁波入射角分别取$\varphi = 0^\circ $,$45^\circ $,对应计算得到的双NACA0012翼型的散射场等值线分布如图 9所示,基本与文献[13]的精确控制法结果一致。从图 9可以看到,在双翼型之间的区域,散射波叠加作用显著,电磁干扰较强;而且随着入射角的改变,干扰作用的效果也存在差异。
 |
| 图 9 双NACA0012翼型散射场等值线分布 |
为了进一步验证本文算法处理多体干扰问题的能力,给出飞机投弹时出现的复杂多体干扰电磁散射场算例。飞机模型源自文献[14],机体长取为$8\lambda $,通过对飞机下表面修形来模拟弹舱,炸弹用椭圆体表示。计算域为$20\lambda \times 20\lambda $,电磁波入射角取$\varphi = 135^\circ $,对应电磁波从飞机前下方照射,计算得到的散射场等值线分布如图 10所示。从图中可以看出飞机投弹与不投弹时的散射场多体干扰情况。不投弹时,只在飞机前部的下方位置附近,由于机头与机身的干扰,局部存在散射场的叠加效应外,其他地方的散射场大体上呈现出均匀的环绕分布,强散射方向出现在双站角$135^\circ $方向和$225^\circ $方向;当飞机弹舱打开,进行投弹时,在飞机下方,除了飞机自身各个部件的干扰以外,炸弹与飞机之间也存在强烈的电磁散射干扰,散射场方向发生改变,最强散射仅出现在双站角$135^\circ $方向。
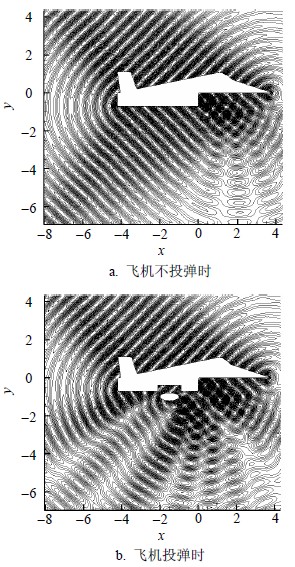 |
| 图 10 飞机投弹与不投弹时的散射场分布 |
本文研究和发展了求解电磁散射问题的基于WENO重构的时域无网格算法。算例表明:本文算法相较于通常的线性重构算法,计算得到的数值解能更接近理论解。由于该算法是基于无网格点云发展的,计算区域的离散只涉及布点,适合处理多体干扰等复杂情形。
| [1] | 苏敏, 陈刚, 童创明. FVTD在电磁散射问题中的应用[J]. 航天电子对抗, 2008, 24(3): 56-58.SU Min, CHEN Gang, TONG Chuang-ming. Application of FVTD method in CEM problems[J]. Aerospace Electronic Warfare, 2008, 24(3): 56-58. |
| [2] | 陈红全. 求解Euler方程的隐式无网格算法[J]. 计算物理, 2003, 20(1): 9-13.CHEN Hong-quan. Implicit gridless method for Euler equations[J]. Chinese Journal of Computational Physics, 2003, 20(1): 9-13. |
| [3] | ZHAO Mei-ling, NIE Yu-feng. A study of boundary conditions in the meshless local Petrov-Galerkin (MLPG) method for electromagnetic field computations[J]. CMES, 2008, 37(2): 97-112. |
| [4] | YU Yi-qiang, CHEN Zhi-zhang. A 3D radial point interpolation method for meshless time-domain modeling[J]. IEEE Transactions on Microwave Theory and Techniques, 2009, 57(8): 2015-2020. |
| [5] | LAI Sheng-jian, WANG Bing-zhong, DUAN Yong. Meshless radial basis function method for transient electromagnetic computations[J]. IEEE Transactions on Magnetics, 2008, 44(10): 2288-2295. |
| [6] | MIRZAVAND R, ABDIPOUR A, MORADI G, et al. Full-wave semiconductor devices simulation using meshless and finite-difference time-domain approaches[J]. IET Microwaves, Antennas & Propagation, 2011, 5(6): 685-691. |
| [7] | LIU G R, GU Y T. 无网格法理论及程序设计[M]. 王建明, 周学军, 译. 济南: 山东大学出版社, 2008.LIU G R, GU Y T. An introduction to meshfree methods and their programming[M]. Translated by WANG Jian-ming, ZHOU Xue-jun. Jinan: Shandong University Press, 2008. |
| [8] | LIU Xu-dong, OSHER S, CHAN T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Physics, 1994, 115(1): 200-212. |
| [9] | GEROLYMOS G A, SENECHAL D, VALLET I. Very-high-order weno schemes[J]. Journal of Computational Physics, 2009, 228: 8481-8524. |
| [10] | 高煜堃, 陈红全. 基于非结构网格格点FVTD算法的电磁散射模拟[J]. 南京航空航天大学学报, 2013, 45(3): 415-423.GAO Yu-kun, CHEN Hong-quan. Electromagnetic scattering simulation based on cell-vertex unstructured-grid FVTD algorithm[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(3): 415-423. |
| [11] | JIANG Guang-shan, SHU Chi-wang. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126: 202-228. |
| [12] | HALLEROD T, RYLANDER T. Electric and magnetic losses modeled by a stable hybrid with explicit-implicit time-stepping for Maxwell's equations[J]. Journal of Computational Physics, 2008, 227: 4499-4511. |
| [13] | CHEN Hong-quan, SUI Hong-tao. New time-explicit asymptotic method for the solution of an exact controllability problem of scattering waves[J]. Chinese Journal of Aeronautics, 2000, 13(2): 80-85. |
| [14] | BESPALOV A. Application of fictitious domain method to the solution of the helmholtz equation in unbounded domain[R]. INRIA 1797. Le Chesnay: INRIA, 1992. |
 2015, Vol. 44
2015, Vol. 44
