车辆换道模型是微观交通仿真中的重要组成部分,换道模型的优劣直接影响着仿真结果。由于换道过程中的运动学过程较为复杂、微观数据难以获取、驾驶员在换道过程中的心理和生理反应难以量化等问题,导致对换道模型的研究相对滞后[1]。现有的微观交通仿真系统中的换道模型不能模拟换道车辆为实施换道而动态调整加速度的行为,且对安全换道距离的分析也没有考虑到所有近邻车辆的整体影响[2]。 本文从运动学角度出发,对车辆换道过程进行分析,着重关注在换道过程中换道车辆在不同时间与近邻车辆的相互影响。通过定义换道过程中的临界状态时间点,分析不同交通参数下的不同临界状态时间顺序,并建立通用的安全换道模型。与其他安全换道模型不同,本文考虑了车辆为成功实施换道自适应的调整自身纵向加速度的行为,以提高微观交通仿真系统的精度。
1 相关工作车辆换道涉及运动学、心理-生理学等理论,是一个高度智能化的复杂过程。而换道模型对换道过程描述的准确程度直接影响着仿真精度。
现有的换道模型研究大多关注于交通状况对驾驶员换道决策的影响。文献[3]提出了一种基于规则的最小化交通流减速的换道模型,文献[4]提出了一种微观的基于模糊推理的换道模型,文献[5]研究了基于元胞自动机的非对称车道换道规则,文献[6]提出了一种可集成于跟驰模型的换道决策模型,文献[7]则通过运动学对换道超车过程进行分析。
在微观交通仿真中,影响驾驶员换道决策的因素较真实换道场景少[8],主要包括:驾驶员主观策略、仿真车辆的路径、近邻车辆的行驶状态(速度、加速度、位置、车辆类型)、道路状况(车辆密度、道路宽度)和信号灯等。
现有的微观交通仿真系统,包括VISSIM[9]、PARAMICS[10]、AIMSUN[11]和MITSIM[12]等,均采用基于规则的换道模型。以MITSIM为例,其换道模型基于GIPPS模型[13]。根据换道的驱动条件,换道分为强制性换道和任意性换道。在强制性换道中不考虑驾驶员主观因素的影响,即使目标车道间距较小,也以一定的概率强制实施换道。而在任意性换道中则要考虑换道环境对换道决策的影响,通过换道判断、换道检测及换道实施3个步骤描述和实施换道行为。
在现有微观交通仿真系统采用的换道模型中,不同仿真系统采用了不同的换道决策规则,而对安全换道距离的计算都是在假设车辆在道路中轴线行驶的情况下,并采用简单的匀加速度的换道模型。这类模型无法模拟真实换道场景中,车辆为实施换道而改变自身加速度的行为。
2 换道过程分析 2.1 换道问题定义微观交通仿真中的换道问题可定义为:每一个仿真时间步中,已知换道车辆和其近邻车辆的行驶状态,判断此时车辆是否可以安全地实施换道。
在微观交通仿真系统中,车辆的位置通常用车辆的几何中心点坐标表示。将车辆D的轮廓近似看作矩形,车辆D的长度和宽度分别记为LD和${w_D}$,其几何中心PD即为仿真中的车辆坐标点。定义车辆的4个顶点为:左前点$P_D^{{\text{LF}}}$、右前点$P_D^{{\text{RF}}}$、左后点$P_D^{{\text{LB}}}$和右后点$P_D^{{\text{RB}}}$;任意时刻t车辆D的中轴线与道路行驶方向的夹角为$\theta (t)$。
可知,t时刻车辆D的4个顶点坐标都可以用$(P_{xD}^{},P_{yD}^{})$表示,即:
| $\begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(P_{xD}^{{\text{LF}}},P_{yD}^{{\text{LF}}}) = \hfill \\ \left( {P_{xD}^{} + \frac{{{L_D}}}{2}\cos \theta - \frac{{{w_D}}}{2}\sin \theta ,P_{yD}^{} + \frac{{{w_D}}}{2}\cos \theta + \frac{{{L_D}}}{2}\sin \theta } \right) \hfill \\ \end{gathered} $ | (1) |
| $\begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(P_{xD}^{{\text{RB}}},P_{yD}^{{\text{RB}}}) = \hfill \\ \left( {P_{xD}^{} - \frac{{{L_D}}}{2}\cos \theta + \frac{{{w_D}}}{2}\sin \theta ,P_{yD}^{} - \frac{{{w_D}}}{2}\cos \theta - \frac{{{L_D}}}{2}\sin \theta } \right) \hfill \\ \end{gathered} $ | (2) |
| $\begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(P_{xD}^{{\text{RF}}},P_{yD}^{{\text{RF}}}) = \hfill \\ \left( {P_{xD}^{} + \frac{{{L_D}}}{2}\cos \theta + \frac{{{w_D}}}{2}\sin \theta ,P_{yD}^{} - \frac{{{w_D}}}{2}\cos \theta + \frac{{{L_D}}}{2}\sin \theta } \right) \hfill \\ \end{gathered} $ | (3) |
| $\begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(P_{xD}^{{\text{LB}}},P_{yD}^{{\text{LB}}}) = \hfill \\ \left( {P_{xD}^{} - \frac{{{L_D}}}{2}\cos \theta - \frac{{{w_D}}}{2}\sin \theta ,P_{yD}^{} + \frac{{{w_D}}}{2}\cos \theta - \frac{{{L_D}}}{2}\sin \theta } \right) \hfill \\ \end{gathered} $ | (4) |
将换道过程分为5个临界状态时间点、4个阶段:
1) 换道初始状态t0。车辆D在t0时刻开始,产生横向加速度。换道时车辆D将不会与车辆C发生碰撞,所以不再需要与车辆C保持安全的相对速度。换道初始状态示意图如图 1所示,图中${S_D}(t)$、$S_D^b(t)$、$S_D^f(t)$分别表示车辆D与车辆C、B、A之间的距离。
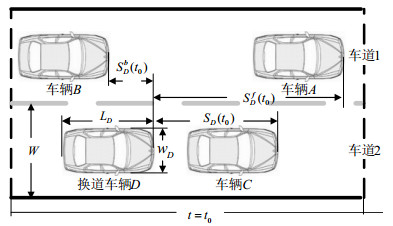 | 图 1 换道初始状态示意图 |
2) 进入目标车道状态t1。此时车辆D的左前方的边界点与道路的边界点重合。从t1时刻开始,车辆B将可能与车辆D发生碰撞。t1时刻为车辆D与车辆B的关系临界点,t1时刻前,车辆B的行驶状态与车辆D无关,t1时刻后,车辆B将受车辆D的影响。进入目标车道状态示意图如图 2所示。
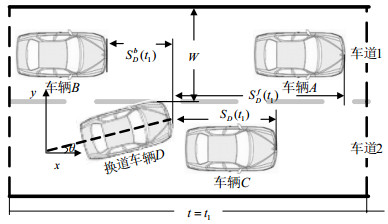 | 图 2 进入目标车道状态示意图 |
3) 当前车道碰撞临界状态t2。此时,换道车辆D的右前边界点$P_D^{{\text{RF}}}$与当前车道前车C的左后边界点$P_C^{\operatorname{LB} }$的y轴坐标相同。在换道过程中,车辆D的右前边界点$P_D^{\operatorname{RF} }$的x坐标值最大。若车辆D与车辆C发生碰撞,最先接触的必然为点$P_D^{\operatorname{RF} }$。t2时刻为车辆C与车辆D的关系临界时间点:t2时刻之前,车辆D会受到车辆C的影响,而t2时刻后,车辆D的行驶状态将与车辆C无关。当前车道碰撞临界状态示意图如图 3所示。
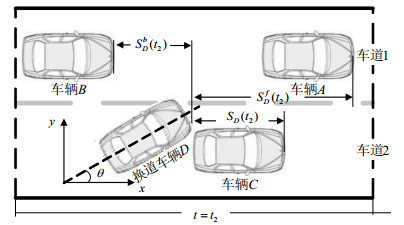 | 图 3 当前车道碰撞临界状态示意图 |
4) 目标车道碰撞临界状态t3。此时换道车辆D的左后边界点$P_D^{\operatorname{LB} }$与目标车道最近的后车B的右前边界点$P_B^{\operatorname{RF} }$的y轴坐标相同。该状态为车辆B与车辆D发生碰撞的临界状态,若在t3时刻之前车辆B并未与车辆C发生碰撞,且车辆B能在t3时刻降速至不高于此时车辆D的速度,则在t3时刻后即使车辆D以最大减速度减速,车辆B也不会与车辆D发生碰撞,此时车辆D与车辆B的安全换道距离最小。若车辆B不能在t3时刻降速至不高于此时车辆D的速度,需考虑两车的初始车头间距是否允许车辆B在t3时刻后减速并能降速至不高于此时车辆D的速度。目标车道碰撞临界状态示意图如图 4所示。
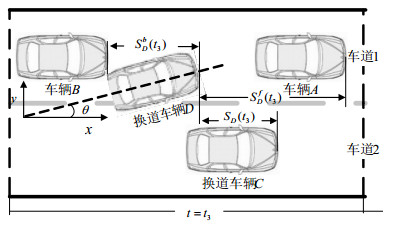 | 图 4 目标车道碰撞临界状态示意图 |
5) 换道完成状态t4。此时,车辆D不会再产生横向位移,其横向加速度和横向速度都为0。达到此状态后,车辆D结束换道行为,其行驶状态转换为以车辆A为目标的跟驰状态。若在此时或此时之前的某一时刻,车辆D能降速至不高于车辆A的速度,则在换道过程结束后两车不会发生碰撞。若此时车辆D无法降速至不高于车辆A的速度,则车辆D需要在此时与车辆A保持一个安全距离使车辆D在进入跟驰状态后不会与车辆A发生碰撞。换道完成状态示意图如图 5所示。
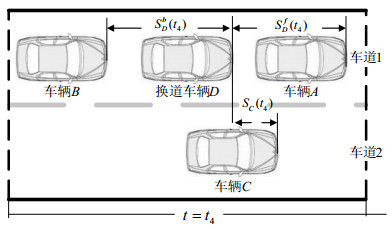 | 图 5 换道完成状态示意图 |
在本文的换道模型中,假设车辆在换道各状态中可使用不同的纵向加速度(t1、t2、t3的大小和纵向加速度的取值是相互影响的)和在同一阶段使用不变的纵向加速度,以模拟真实车辆在换道过程中根据相关车辆的距离、速度等信息自适应调节自身速度从而达到换道目的的行为。
由于换道过程中换道各临界状态时间受到各种参数的影响,故换道中“进入目标车道状态”“当前车道碰撞临界状态”和“目标车道碰撞临界状态”的时间顺序无法确定。临界状态时间的出现顺序分3种情况,即t1<t2<t3、t2<t1<t3和t1<t3<t2。虽然该顺序会受到换道时车辆的纵向加速度、换道完成的时间等的影响,但很大程度上该顺序是由车辆在道路中的初始横向位置决定的。
2.4 横向加速度模型实际生活中车辆在换道过程中横向加速度的变化较为复杂,为计算换道的各临界状态时间,采用较简单但接近真实情况的正弦函数形式的横向加速度模型[14],加速度${a_y}(t)$可表示为:
| ${a_y}(t) = \left\{ \begin{gathered} \frac{{2{\text{\pi }}W}}{{t_4^2}}\sin \frac{{2{\text{\pi }}t}}{{{t_4}}}\quad {t_0} \leqslant t \leqslant {t_4} \hfill \\ 0\quad \quad \quad \quad t < {t_0}\;或\;t > {t_4} \hfill \\ \end{gathered} \right.$ | (5) |
式中,W为换道横向位移;t4为换道完成时间。对式(5)两次积分,可得换道任意时刻车辆的横向位移模型:
| $y(t) = \left\{ \begin{gathered} W\quad \quad \quad \;\;t \geqslant {t_4} \hfill \\ \frac{{ - W}}{{2{\text{\pi }}}}\sin \frac{{2{\text{\pi }}t}}{{{t_4}}} + \frac{{Wt}}{{{t_4}}}\quad {t_0} \leqslant t \leqslant {t_4} \hfill \\ 0\quad \quad \quad \quad t \leqslant {t_0} \hfill \\ \end{gathered} \right.$ | (6) |
任意时刻$\theta (t)$可由此时换道车辆的横向速度${v_y}(t)$和纵向速度${v_x}(t)$计算得:
| $\theta (t) = \arctan \frac{{\partial y/\partial t}}{{\partial x/\partial t}} = \arctan \frac{{{v_y}(t)}}{{{v_x}(t)}}$ | (7) |
当换道车辆在换道各状态的纵向加速度可变时,临界状态时间的先后顺序对换道车辆纵向加速度的取值产生影响,并导致安全换道距离的计算产生误差。
以t1<t2<t3为例,在t=t1时,即换道车辆进入目标车道状态,如图 2所示,此时换道车辆D的左前边界点进入目标车道:$P_{yD}^{{\text{LF}}} = W$。t0到t1阶段参考点PD的横向位移为:
| $\begin{gathered} \;\;\;\;\;\;\;\;\;P_{yD}^{}({t_1}) - P_{yD}^{}({t_0}) = \hfill \\ W - P_{yD}^{}({t_0}) - \frac{{{w_D}}}{2}\cos \theta ({t_1}) - \frac{{{L_D}}}{2}\sin \theta ({t_1}) \hfill \\ \end{gathered} $ | (8) |
根据换道横向位移公式(6),参考点PD的横向位移可表示为:
| $\begin{gathered} \;P_{yD}^{}({t_1}) - P_{yD}^{}({t_0}) = \frac{{ - W}}{{2{\text{\pi }}}}\sin \frac{{2{\text{\pi }}{t_1}}}{{{t_4}}} + \frac{{W{t_1}}}{{{t_4}}} = \hfill \\ W - P_{yD}^{}({t_0}) - \frac{{{w_D}}}{2}\cos \theta ({t_1}) - \frac{{{L_D}}}{2}\sin \theta ({t_1}) \hfill \\ \end{gathered} $ | (9) |
根据任意时刻t与$\theta $的关系式(7),可得:
| $\tan \theta ({t_1}) = \frac{{\partial y({t_1})/\partial t}}{{\partial x({t_1})/\partial t}} = \frac{{ - \frac{W}{{t_4^{}}}\cos \frac{{2{\text{\pi }}{t_1}}}{{{t_4}}} + \frac{W}{{{t_4}}}}}{{{v_{xD}}({t_0}) + {a_{xD}}({t_0})({t_1} - {t_0})}}$ | (10) |
可知此时的$\sin \theta $和$\cos \theta $表达式:
| $\sin \theta ({t_1}) = \frac{{\partial y({t_1})/\partial t}}{{\sqrt[{}]{{{{(\partial x({t_1})/\partial t)}^2} + {{(\partial y({t_1})/\partial t)}^2}}}}}$ | (11) |
| $\cos \theta ({t_1}) = \frac{{\partial x({t_1})/\partial t}}{{\sqrt[{}]{{{{(\partial x({t_1})/\partial t)}^2} + {{(\partial y({t_1})/\partial t)}^2}}}}}$ | (12) |
将式(11)、(12)带入式(9),可得:
| $\begin{gathered} \;\;\;\;\;\;\;\;\;\;\frac{{ - W}}{{2{\text{\pi }}}}\sin \frac{{2{\text{\pi }}{t_1}}}{{{t_4}}} + \frac{{W{t_1}}}{{{t_4}}} - W + P_{yD}^{}({t_0}) = \hfill \\ \frac{{ - {w_D}({v_{xD}}({t_0}) + {a_{xD}}({t_0})({t_1} - {t_0})) - {L_D}\left( { - \frac{W}{{{t_4}}}\cos \frac{{2{\text{\pi }}{t_1}}}{{{t_4}}} + \frac{W}{{{t_4}}}} \right)}}{{2\sqrt {{{\left( { - \frac{W}{{{t_4}}}\cos \frac{{2{\text{\pi }}{t_1}}}{{{t_4}}} + \frac{W}{{{t_4}}}} \right)}^2} + {{({v_{xD}}({t_0}) + {a_{xD}}({t_0})({t_1} - {t_0}))}^2}} }} \hfill \\ \end{gathered} $ | (13) |
可看出,此时t1的计算只由换道车辆的初始速度${v_{xD}}({t_0})$、${t_0} \to {t_1}$阶段的纵向加速度${a_{xD}}({t_0})$、换道横位移W、换道车辆的长度LD、宽度${w_D}$、初始横坐标${P_{yD}}({t_0})$及换道过程的持续时间t4决定。对这些参数赋值,即可通过式(13)求解t1。由于t1同时存在于余弦函数中,导致计算t1的数值解存在一定困难。本文通过无限逼近法求解t1的近似值,也用于对其他临界状态时间的求解。
通过类似的方式,可以得到t2和t3的方程式以得到t2和t3的近似解,以及其他临界状态时间顺序${t_2} < {t_1} < {t_3}$和${t_1} < {t_3} < {t_2}$时,t1、t2和t3的近似解。
3.2 临界状态顺序判断由于换道临界状态时间的顺序存在3种可能性,故在换道计算中,首先需通过各项参数的取值确定换道临界状态时间的顺序。临界状态时间顺序的判断过程如下:
1) 分别假设t1和t2为换道初始状态后的下一个状态,即可计算出该假设下的t'1和t'2;
2) 可证明,$\min ({t'_1},{t'_2})$的假设为真,即$\min ({t'_1},{t'_2})$为t0后的下一个状态;
3) 若${t_2} < {t_1}$,则换道临界状态时间的顺序只能为${t_2} < {t_1} < {t_3}$;若${t_1} < {t_2}$,则需要判断t2和t3的大小;
4) 分别假设t2和t3为“进入目标车道状态”后的下一个状态,可计算出该假设下的t'2和t'3;
5) 当$\min ({t'_2},{t'_3}) = {t'_2}$时,换道临界状态时间的顺序为${t_1} < {t_2} < {t_3}$;当$\min ({t'_2},{t'_3}) = {t'_3}$时,换道临界状态时间的顺序为${t_1} < {t_3} < {t_2}$。
3.3 安全换道距离分析在完整的换道环境中,换道车辆D需在${t_0} \leqslant t \leqslant {t_2}$时、${t_1} \leqslant t \leqslant {t_3}$时、${t_1} \leqslant t \leqslant {t_4}$时分别于车辆C、B、A保持一定的安全距离才能避免在换道过程中与之发生碰撞。即车辆D在实施换道行为前,需预判其与车辆C、B、A的距离${S_D}(t)$、$S_D^b(t)$、$S_D^f(t)$。
1) 与车辆C的安全换道距离:换道初始时刻两车的安全换道间距可由t2时刻车辆D与车辆C的车头间距表示为:
| $\begin{gathered} \;\;{S_D}({t_0}) = \Delta {P_{xD}}({t_2} - {t_0}) - \Delta {P_{xC}}({t_2} - {t_0}) - \hfill \\ \frac{{{L_D}}}{2} + \frac{{{L_D}}}{2}\cos \theta ({t_2}) + \frac{{{w_D}}}{2}\sin \theta ({t_2}) + {S_D}({t_2}) \hfill \\ \end{gathered} $ | (14) |
可知,当${S_D}({t_2})$取值最小时,${S_D}({t_0})$也最小。t2时刻两车不发生碰撞的车头间距${S_D}({t_2})$需满足:
| ${S_D}({t_2}) \geqslant {L_C} + h$ | (15) |
式中,h为常数安全距离,表示两车静止时的最小间距。
当${S_D}({t_2}) = {L_C} + h$时,${S_D}({t_0})$的最小值${S_D}({t_0})'$为:
| $\begin{gathered} \;\;{S_D}({t_0})' = \Delta {P_{xD}}({t_2} - {t_0}) - \Delta {P_{xC}}({t_2} - {t_0}) - \hfill \\ \frac{{{L_D}}}{2} + \frac{{{L_D}}}{2}\cos \theta ({t_2}) + \frac{{{w_D}}}{2}\sin \theta ({t_2}) + {L_C} + h \hfill \\ \end{gathered} $ | (16) |
2) 与车辆B的安全换道距离:换道初始时刻两车的安全换道间距可由t3时刻车辆D与车辆B的车头间距表示为:
| $\begin{gathered} \;S_D^b({t_0}) = \Delta {P_{xB}}({t_3} - {t_0}) - \Delta {P_{xD}}({t_3} - {t_0}) + \hfill \\ \frac{{{L_D}}}{2} - \frac{{{L_D}}}{2}\cos \theta ({t_3}) - \frac{{{w_D}}}{2}\sin \theta ({t_3}) + S_D^b({t_3}) \hfill \\ \end{gathered} $ | (17) |
可知,当$S_D^b({t_3})$取值最小时,$S_D^b({t_0})$也最小。t3时刻两车不发生碰撞的车头间距需满足:
| $S_D^b({t_3}) \geqslant {L_D}\cos \theta ({t_3}) + h$ | (18) |
当$S_D^b({t_3}) = {L_D}\cos \theta ({t_3}) + h$时,$S_D^b({t_0})$的最小值为:
| $\begin{gathered} \;S_D^b({t_0})' = \Delta {P_{xB}}({t_3} - {t_0}) - \Delta {P_{xD}}({t_3} - {t_0}) + \hfill \\ \frac{{{L_D}}}{2} + \frac{{{L_D}}}{2}\cos \theta ({t_3}) - \frac{{{w_D}}}{2}\sin \theta ({t_3}) + h \hfill \\ \end{gathered} $ | (19) |
3) 与车辆A的安全距离:换道初始时刻两车的安全换道间距可由t4时刻车辆D与车辆A的车头间距表示为:
| $S_D^f({t_0}) = \Delta {P_{xD}}({t_4} - {t_0}) - \Delta {P_{xA}}({t_4} - {t_0}) + S_D^f({t_4})$ | (20) |
可知,当$S_D^f({t_4})$取值最小时,$S_D^f({t_0})$也最小。t4时刻两车不发生碰撞的车头间距需满足:
| $S_D^f({t_4}) \geqslant {L_A} + h + \frac{{{v_{xA}}{{({t_4})}^2} - {v_{xD}}{{({t_4})}^2}}}{{2a_{xD}^{ - \max }}}$ | (21) |
$S_D^f({t_4}) = {L_A} + h + [{v_{xA}}{({t_4})^2} - {v_{xD}}{({t_4})^2}]/2a_{xD}^{ - \max }$时,$S_D^f({t_0})$的最小值为:
| $\begin{gathered} S_D^f({t_0})' = \Delta {P_{xD}}({t_4} - {t_0}) - \Delta {P_{xA}}({t_4} - {t_0}) + \hfill \\ {L_A} + h + \frac{{{v_{xA}}{{({t_4})}^2} - {v_{xD}}{{({t_4})}^2}}}{{2a_{xD}^{ - \max }}} \hfill \\ \end{gathered} $ | (22) |
对于每一种临界状态时间顺序,最小安全换道距离的计算都要考虑该时间内纵向加速度的变化。
3.4 自适应加速度计算加速度自适应的换道模型在判断换道过程中,要考虑各阶段纵向加速度的取值对换道临界状态时间顺序的影响。不同的临界状态时间顺序下,计算纵向加速度的方法不同。本文通过建立约束表达式的方式描述纵向加速度的可能取值。以${t_1} < {t_2} < {t_3}$情况为例,纵向加速度集合的约束表达式为:
| $\left\{ \begin{gathered} \left. \begin{gathered} f({t_1})|{t_1} < {t_2} < {t_3} \hfill \\ f(t_2^{})|{t_1} < {t_2} < {t_3} \hfill \\ f({t_3})|{t_1} < {t_2} < {t_3} \hfill \\ \end{gathered} \right\rangle 各临界状态时间函数 \hfill \\ {t_1} < {t_2} < {t_3} \hfill \\ \left. \begin{gathered} \Delta {P_{xD}}({t_2} - {t_1}) - \Delta {P_{xC}}({t_2} - {t_1}) \geqslant {H_C} \hfill \\ \Delta {P_{xD}}({t_1} - {t_0}) - \Delta {P_{xC}}({t_1} - {t_0}) \geqslant {H_C} \hfill \\ \end{gathered} \right\rangle 与车辆C的安全距离 \hfill \\ \left. \begin{gathered} \Delta {P_{xB}}({t_3} - {t_2}) - \Delta {P_{xD}}({t_3} - {t_2}) \geqslant {H_B} \hfill \\ \Delta {P_{xB}}({t_2} - {t_1}) - \Delta {P_{xD}}({t_2} - {t_1}) \geqslant {H_B} \hfill \\ \end{gathered} \right\rangle 与车辆B的安全距离 \hfill \\ \left. \begin{gathered} \Delta {P_{xD}}({t_4} - {t_3}) - \Delta {P_{xA}}({t_4} - {t_3}) \geqslant {H_A} \hfill \\ \Delta {P_{xD}}({t_3} - {t_2}) - \Delta {P_{xA}}({t_3} - {t_2}) \geqslant {H_A} \hfill \\ \Delta {P_{xD}}({t_2} - {t_1}) - \Delta {P_{xA}}({t_2} - {t_1}) \geqslant {H_A} \hfill \\ \end{gathered} \right\rangle 与车辆A的安全距离 \hfill \\ \end{gathered} \right.$ | (23) |
即以换道各阶段的纵向加速度为未知数,通过各临界状态时间函数、临界状态时间约束、各阶段换道车辆与邻近车辆的安全距离约束关系联立求解。当约束表达式有解时,该组解的纵向加速度的集合,即车辆可实施换道的纵向加速度取值。式中车辆D与车辆A、B、C需保持的可换道的最小安全距离HA、HB、HC是由两车的车头距、相关车辆长度、宽度、常数安全距离h、临界状态时间和该时间换道车辆偏移角度$\theta $决定的。
4 模型精度验证为了验证换道模型的精度,本文使用微观交通仿真系统MTSS[15],建立了一条长度为5 km的2车道道路,设置仿真时间为1 000步,即一个仿真周期为逻辑时间0.1 s,每一个仿真时间步设置较容易触发的换道意图产生规则:当前行驶速度小于期望行驶速度的一半,即产生换道意图。同时不使用换道决策规则,即不考虑个体差异,产生换道意图后即尝试换道,若换道未成功则在50个时间步后继续尝试换道。通过多次仿真实验,对比了不同交通密度下加速度自适应换道模型与匀加速度换道模型的换道成功率,两种换道模型换道成功率对比图如图 6所示。
 | 图 6 两种换道模型换道成功率对比图 |
图中纵坐标为该仿真时间内所有车辆的换道成功率,即成功换道次数与产生换道意图次数的比值。可见,使用加速度自适应的换道模型的换道成功率较匀加速度的换道模型高,即加速度自适应的换道模型所计算的安全换道距离更准确,模型精度更高。
5 结论本文分析了车辆在换道过程中与近邻车辆的相互影响的分析,将换道过程分为4个独立的阶段。通过改变每个阶段的纵向加速度,以在微观交通仿真系统中模拟车辆加速度自适应变化的过程。仿真结果显示,相对于匀加速的换道模型,本文提出的换道模型的换道成功率更高,即模型的精度更高。
| [1] | BEN-AKIVA M E, CHOUDURY C, TOLEDO T. Lane changing models[C]//Second International Symposium of Transport Simulation(ISTS06). Lausanne, Switzerland: EPFL, 2006. |
| [2] | TANG Tie-qiao, HUANG Hai-jun, WONG S C, et al. Lane changing analysis for two-lane traffic flow[J]. Acta Mechanica Sinica, 2007, 23(1): 49-54. |
| [3] | KESTING A, TREIBER M, HELBING D. General lane-changing model mobil for car-following models[J]. Journal of the Transportation Research Board, 2007, 1999(1): 86-94. |
| [4] | ERRAMPALLI M, OKUSHIMA M, AKIYAMA T. Fuzzy logic based lane change model for microscopic traffic flow simulation[J]. Journal of Advanced Computational Intelligence and Intelligent Informatics, 2008, 12(2): 172-181. |
| [5] | HABEL L, SCHRECKENBERG M. Asymmetric lane change rules for a microscopic highway traffic model[C]// 11th International Conference on Cellular Automata for Research and Industry, ACRI 2014. Krakow, Poland: Springer International Publishing, 2014: 620-629. |
| [6] | SCHAKEL W J, KNOOP V L, VAN AREM B. Integrated lane change model with relaxation and synchronization[J]. Transportation Research Record, 2012, 2316(1): 47-57. |
| [7] | LI F, GAO L, LI X. Research on lane change timing model considering the influence of four surrounding vehicles[C]// Transportation Electrification Asia-Pacific (ITEC Asia-Pacific), 2014 IEEE Conference and Expo. Beijing: IEEE, 2014: 1-6. |
| [8] | HIDAS P. Modeling lane changing and merging in microscopic traffic simulation[J]. Transportation Research Part C, 2002, 10(5): 351-371. |
| [9] | FELLENDORF M. VISSIM: A microscopic simulation tool to evaluate actuated signal control including bus priority[C]//64th Institute of Transportation Engineers Annual Meeting. [S.l.]: Springer, 1994: 1-9. |
| [10] | CAMERON D B, DUNCAN I D. Paramics—parallel microscopic simulation of road traffic[J]. The Journal of Supercomputing, 1996, 10(1): 25-53. |
| [11] | BARCELO J. Models, traffic models, simulation, and traffic simulation[M]. New York: Springer, 2010. |
| [12] | HASAN M. Evaluation of ramp control algorithms using a microscopic traffic simulation laboratory, MITSIM[D]. USA: Massachusetts Institute of Technology, 1999. |
| [13] | GIPPS P G. A model for the structure of lane-changing decisions[J]. Transportation Research Part B: Methodological, 1986, 20(5): 403-414. |
| [14] | 罗强. 面向高速公路行车安全预警的车道偏离及换道模 型研究[D]. 广州: 华南理工大学, 2014. LUO Qiang. Research on lane departure and lane-changing model for highway driving safety warning[D]. Guangzhou: South China University of Technology, 2014. |
| [15] | 赵玉平. 微观交通仿真关键技术及其应用研究[D]. 成 都: 电子科技大学, 2014. ZHAO Yu-ping. Research and applications on key technology of microscopic traffic simulation[D]. Chengdu: University of Electronic Science and Technology of China, 2014. |
 2015, Vol. 44
2015, Vol. 44
