光栅衍射场的模拟计算对于光栅、光子晶体等周期结构的设计与分析[1, 2, 3]都具有重要意义。同时,在半导体微电子制造产业的计量领域,尤其是集成电路结构的分析/测试中,零级衍射场的模拟计算同样有着广泛的应用[4]。对于集成电路中普遍周期性结构的实际测量,模拟计算的效率是一个十分关键的因素。光栅结构的模拟计算方法一般分为标量衍射模型与矢量衍射模型。标量衍射模型计算速度快,适用于大尺寸微米量级周期结构的分析测量。但是随着半导体产业持续往更先进的技术节点迈进,工程实际中对模拟计算的精度要求也不断提高,矢量衍射模型逐渐成为主流。其中,基于傅里叶空间展开实现的RCWA[5]是应用最成熟、广泛的方法。RCWA非常适合于垂直侧壁一维光栅结构的衍射模拟,对于任意形貌的复杂周期结构则往往需要通过阶梯近似技术采用传输矩阵法计算[6]。阶梯近似的多层划分对于RCWA的效率影响较大,一些改进的方法有基于坐标变换的C-RCWA[7]、基于快速傅里叶分解(FFF)的微分算法[8]、基于微扰近似的P-RCWA[9]等。但是它们的应用往往具有局限性,坐标变换技术难以处理复杂边界的多层周期结构,P-RCWA则仅能处理侧壁变化微小的光栅结构。其中,FFF微分算法虽然是一种更严格的满足3个傅里叶分解原则的通用方法[8],但是其矩阵计算阶次通常为RCWA的两倍,同时对于复杂结构的垂直矢量场的构造(尤其是二维光栅)较为困难且耗时。
另一方面,上述微分方法不可避免地需要计算特征值这一耗时问题,一些非特征值求解方法如Rayleigh法则局限于深宽比在特定范围的结构。因此,傅里叶空间的层吸收法(SAM)成为本文研究的出发点[10]。基于差分化的实空间或傅里叶空间麦克斯韦旋度方程,针对时谐电磁场问题,文献[10]提出了一种高斯消元计算方法——SAM。其核心思想是通过引入差分矩阵算子,得到沿光栅侧壁方向网格化后的二阶差分方程组;该二阶方程组的系数矩阵(又称波动矩阵)是一个三对角元矩阵,从而可以采用高斯消元将网格方程逐个消去,最后结合边界条件得到待求位置处电磁场问题的解。但是原始的SAM相对于RCWA过程繁琐,矩阵阶次也过大,而且目前只是少量应用于微米量级光子晶体分析中。本文结合RCWA与SAM的计算特点,实现纳米量级任意光栅结构的模拟计算。
1 基本方法图 1为任意角度入射光投射到一维光栅平面的示意图。入射光源 $ {{\mathbf{E}}_{\text{inc}}}$从覆盖层(通常为空气)照射到光栅,其空间入射模型特性由3个角度限定:入射角θ(0°≤θ< 90°)、方位角Φ($0{}^\circ $≤Φ<$360{}^\circ $)、偏振角 $\psi $($0{}^\circ $≤$\psi $<$360{}^\circ $)。当${{\mathbf{E}}_{\text{inc}}}$垂直于入射平面,即$\psi =90{}^\circ $或$270{}^\circ $时为TE偏振;当${{\mathbf{E}}_{\text{inc}}}$平行于入射平面,即$\psi =0{}^\circ $或$180{}^\circ $时为TM偏振。$\Lambda $为光栅周期,电磁衍射模拟问题区域被划分为:覆盖层(折射率为${{n}_{c}}$)、光栅区域(折射率为n)、衬底层(折射率为${{n}_{\text{sub}}}$)。
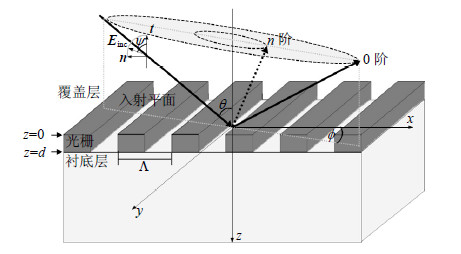 |
| 图1任意角度入射光入射一维光栅平面示意图 |
如果光栅区域为任意复杂光栅结构,则可以采用阶梯近似技术将光栅区域划分为多个小层,如图 2所示,其中i为各小层的层标(i=1~I)。整个问题区域满足弗洛奎特条件,其一维平面衍射为:
| $ \begin{matrix} {{k}_{xm}}={{k}_{0}}{{n}_{c}}\sin \theta -2m{\text{ }\!\!\pi\!\!\text{ }}/{\Lambda }\; \\ {{k}_{lz,m}}=\sqrt{{{\left( {{k}_{0}}{{n}_{l}} \right)}^{2}}-k_{xm}^{2}} \\ \text{if }\operatorname{Re}({{k}_{lz,m}})<\operatorname{Im}({{k}_{lz,m}}),\text{ }{{k}_{lz,m}}=-{{k}_{lz,m}}\text{, }l\in \left\{ c,\text{ sub} \right\} \\ \end{matrix} $ | (1) |
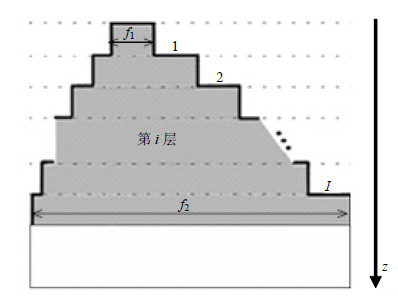 |
| 图2任意光栅结构的阶梯近似剖面示意图 |
式中,m是x方向的衍射阶次; ${{k}_{0}}=2\text{ }\!\!\pi\!\!\text{ }/{{\lambda }_{0}}$是自由空间中的波矢大小( ${{\lambda }_{0}}$为自由空间中入射光波长); $ {{k}_{xm}}$是沿x方向的第m阶谐波波矢大小; $ {{k}_{lz,m}} $是覆盖层与衬底层沿z方向的第m阶谐波波矢大小。
1.1 平面衍射:TE偏振入射对于一维周期结构TE偏振入射的平面衍射情况,其入射场为:
| $ {{E}_{\text{inc},y}}=\exp [-\text{j}{{k}_{0}}{{n}_{c}}(\sin \theta \cdot x+\cos \theta \cdot z)] $ | (2) |
根据RCWA的傅里叶空间展开原则[11],覆盖层与衬底层的衍射场可以表示为:
| $ {{E}_{c,y}}={{E}_{\text{inc},y}}+\sum\limits_{m}{{{R}_{m}}\exp [-\text{j}({{k}_{xm}}x-{{k}_{cz,m}}z)]} $ | (3) |
| $ {{E}_{\text{sub},y}}=\sum\limits_{m}{{{T}_{m}}\exp \{-\text{j}[{{k}_{xm}}x+{{k}_{\text{subz},m}}(z-d)]\}} $ | (4) |
光栅区域的场量为:
| $ {{E}_{gy}}=\sum\limits_{m}{{{S}_{ym}}(z)\exp (-\text{j}{{k}_{xm}}x)} $ | (5) |
| $ {{H}_{gx}}=-j{{\left( \frac{{{\varepsilon }_{0}}}{{{\mu }_{0}}} \right)}^{{1}/{2}\;}}\sum\limits_{m}{{{U}_{xm}}(z)\exp (-\text{j}{{k}_{xm}}x)} $ | (6) |
因此,将式(5)~式(6)代入麦克斯韦旋度方程,可以得到光栅区域傅里叶空间的微分旋度方程。如果按照图 3的梯近似多层结构Yee式网格模型,对该旋度方程差分化,则可进一步得到光栅区域各网格的一阶差分旋度方程:
| $ {{\mathbf{D}}_{i}}\mathbf{S}_{yj}^{i}-{{\mathbf{D}}_{i}}\mathbf{S}_{yj+1}^{i}=-\mathbf{U}_{xj}^{i} $ | (7) |
| $ -{{\mathbf{D}}_{i}}\mathbf{U}_{xj-1}^{i}+{{\mathbf{D}}_{i}}\mathbf{U}_{xj}^{i}=(\mathbf{K}_{x}^{2}-{{\mathbf{E}}_{i}})\mathbf{S}_{yj}^{i} $ | (8) |
式中,j为网格标号(1≤j<≤Ji); $ \mathbf{D}_{i}^{{}} $为对角元为 $ 1/\text{ }\!\!\Delta\!\!\text{ }{{{z}'}_{i}}=1/({{k}_{0}}\text{ }\!\!\Delta\!\!\text{ }{{z}_{i}}) $的对角矩阵; $ \text{ }\!\!\Delta\!\!\text{ }{{z}_{i}} $为第i层的空间步长; $ {{\mathbf{K}}_{x}} $为以 $ {{k}_{xm}}/{{k}_{0}}$为对角元的对角矩阵; $\mathbf{S}_{j}^{i}$、 $\mathbf{U}_{j}^{i}$为光栅区域第i层第j网格处电场/磁场的傅里叶系数向量; $ {{\mathbf{E}}_{i}} $为第i层的介电系数函数对应的托普利兹矩阵(其中 $ E_{mp}^{i}=\varepsilon _{m-p}^{i} $)。双介质周期结构(介质1折射率为 $ {{n}_{1}} $,介质2折射率为 $ {{n}_{2}}$)的介电系数函数 ${{\varepsilon }^{i}}(x)$的傅里叶系数为:
| $ \varepsilon (x)=\sum\limits_{n}{{{\varepsilon }_{n}}\exp \left( \text{j}\frac{2n\text{ }\!\!\pi\!\!\text{ }}{\Lambda }x \right)} $ | (9) |
| $ {{\varepsilon }_{0}}={{n}_{2}}f+{{n}_{1}}(1-f),{{\varepsilon }_{n}}=(n_{2}^{2}-n_{1}^{2})\frac{\sin (n\text{ }\!\!\pi\!\!\text{ }f)}{n\text{ }\!\!\pi\!\!\text{ }} $ | (10) |
式中,f为介质2的宽度在第i层占据单位周期长度的比值(占空比);f1、f2为介质2的上下侧占空比。
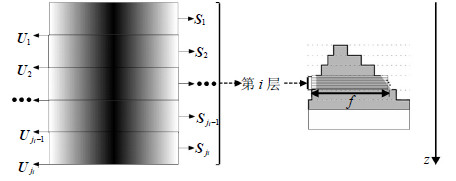 |
| 图3阶梯近似多层结构各层的Yee式网格模型 |
此时,根据一阶差分旋度方程式(7)~式(8),可以给出第i-1层最后一个网格(j=Ji-1)的差分旋度方程与第i层第1个网格的旋度方程,并综合此两组方程可得到第i层的上边界网格差分波动方程:
| $ \mathbf{D}_{i}^{{}}\mathbf{D}_{i-1}^{{}}\mathbf{S}_{y{{J}_{i-1}}}^{i-1}-(\mathbf{D}_{i}^{2}+\mathbf{D}_{i}^{{}}\mathbf{D}_{i-1}^{{}}+\mathbf{A}_{i}^{{}})\mathbf{S}_{y1}^{i}+\mathbf{D}_{i}^{2}\mathbf{S}_{y2}^{i}=0 $ | (11) |
令 $ {{\mathbf{a}}_{i}}=\mathbf{D}_{i}^{2} $, ${{\mathbf{a}}_{i,1}}=\mathbf{D}_{i}^{{}}\mathbf{D}_{i\text{-}1}^{{}}$, ${{\mathbf{b}}_{i,1}}=-\mathbf{D}_{i}^{2}-\mathbf{D}_{i}^{{}}\mathbf{D}_{i\text{-}1}^{{}}-\mathbf{A}_{i}^{{}}$,则第i层的上边界网格波动方程可以改写为:
| $ {{\mathbf{a}}_{i,1}}\mathbf{S}_{y{{J}_{i\text{-}1}}}^{i\text{-}1}+{{\mathbf{b}}_{i,1}}\mathbf{S}_{y1}^{i}+{{\mathbf{a}}_{i}}\mathbf{S}_{y2}^{i}=0 $ | (12) |
并且,根据一阶差分旋度方程式(7)~式(8),可以得到第i层内非上边界网格的重复网格差分波动方程:
| $ \mathbf{D}_{i}^{2}\mathbf{S}_{yj-1}^{i}-(2\mathbf{D}_{i}^{2}+{{\mathbf{A}}_{i}})\mathbf{S}_{yj}^{i}+\mathbf{D}_{i}^{2}\mathbf{S}_{yj+1}^{i}=0 $ | (13) |
式中, $ {{\mathbf{A}}_{i}}=\mathbf{K}_{x}^{2}-\mathbf{E}_{i}^{{}} $。且定义系数矩阵 ${{\mathbf{b}}_{i}}=$$-2\mathbf{D}_{i}^{2}-$${{\mathbf{A}}_{i}}$,则第i层内的重复网格差分波动方程可以改写为:
| ${{\mathbf{a}}_{i}}\mathbf{S}_{yj-1}^{i}+{{\mathbf{b}}_{i}}\mathbf{S}_{yj}^{i}+{{\mathbf{a}}_{i}}\mathbf{S}_{yj+1}^{i}=0$ | (14) |
至此光栅区域非覆盖层、衬底层边界位置的各网格差分波动方程均已给出。
覆盖层、衬底层边界处的网格差分波动方程则通过全场/散射场模型[10]与传输边界条件(全称TBC)给出,如图 4所示。TE偏振入射时,电场源Einc,y设置在覆盖层第0网格处。此时综合覆盖层第-1网格的旋度差分方程(散射场内)与覆盖层第0网格的旋度差分方程(散射场内),并加入TBC边界条件,可以得到第0格的差分波动方程:
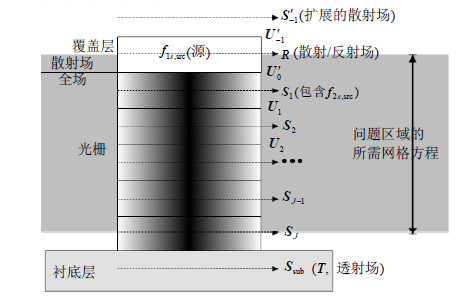 |
| 图4TE偏振平面衍射的全场/散射场模型 |
| $ {{\mathbf{b}}_{0}}\mathbf{R}+{{\mathbf{a}}_{1}}\mathbf{S}_{y1}^{1}=\exp (-\text{j}{{k}_{cz,0}}\Delta z)\mathbf{D}_{1}^{2}{{\mathbf{f}}_{1sy,\text{src}}} $ | (15) |
式中, $ {{\mathbf{b}}_{0}}={{\mathbf{Z}}_{\text{ref}}}\mathbf{D}_{1}^{2}-2\mathbf{D}_{1}^{2}-\mathbf{A}_{c}^{{}}$; $ {{\mathbf{Z}}_{\text{ref}}} $是TBC边界条件定义下的对角矩阵; $ {{\mathbf{A}}_{c}}=\mathbf{K}_{x}^{2}-\mathbf{E}_{c}^{{}} $;f1sy,src是Einc,y的傅里叶系数组成的列向量[… 0 1 0 …]T。
综合覆盖层第0网格的旋度差分方程(散射场内)与阶梯近似第1层第1网格的旋度差分方程(全场内),可以得到阶梯近似第1层第1网格的差分波动方程(包括两个形式):
| $ \begin{align} & \mathbf{a}_{1}^{{}}{{{\mathbf{{S}'}}}_{y0}}+{{\mathbf{b}}_{1}}\mathbf{S}_{y1}^{1}+\mathbf{a}_{1}^{{}}\mathbf{S}_{y2}^{1}= \\ & \mathbf{D}_{1}^{{}}{{\mathbf{f}}_{1ux,\text{src}}}-\exp (-\text{j}{{k}_{cz,0}}\Delta z)\mathbf{D}_{1}^{2}{{\mathbf{f}}_{1sy,\text{src}}} \\ \end{align} $ | (16) |
或
| $ \mathbf{a}_{1}^{{}}\mathbf{R}+{{\mathbf{b}}_{1}}\mathbf{S}_{y1}^{1}+\mathbf{a}_{1}^{{}}\mathbf{S}_{y2}^{1}=-\mathbf{D}_{1}^{2}{{\mathbf{f}}_{1sy,\text{src}}} $ | (17) |
式中, ${{\mathbf{f}}_{1ux,\text{src}}}$为Einc,y对应磁场源的傅里叶系数的列向量[…0 -jcosθ 0 …]T。式(16)的右侧源比式(17)右侧源包含了更多的近似。
衬底层与光栅区域边界只需考虑TBC边界条件,阶梯近似第I层第JI格(最后一格)的波动方程为:
| $ {{\mathbf{a}}_{I}}\mathbf{S}_{y{{J}_{I}}-1}^{I}+{{\mathbf{b}}_{I,{{J}_{I}}}}\mathbf{S}_{y{{J}_{I}}}^{I}=0 $ | (18) |
式中, $ {{\mathbf{b}}_{I,{{J}_{I}}}}={{\mathbf{b}}_{I}}+{{\mathbf{a}}_{I}}{{\mathbf{Z}}_{\text{trn}}} $, $ {{\mathbf{Z}}_{\text{trn}}} $是TBC边界条件定义下的对角矩阵。
最后,从覆盖层到衬底层逐网格排列出一个线性方程组(依次包括:式(15)、式(16)、式(17)、式(12)、式(14)、式(18)),最终可以写成一个形如式(22)的块矩阵波动方程。其中,f1、f2根据式(15)、式(16)、式(17)可以表示为两种形式:
| $ \left( \begin{matrix} {{\mathbf{f}}_{1}} \\ {{\mathbf{f}}_{2}} \\ \end{matrix} \right)=\left( \begin{matrix} \exp (-\text{j}{{k}_{cz,0}}\Delta z)\mathbf{D}_{1,j}^{2}{{\mathbf{f}}_{1sy,\text{src}}} \\ \mathbf{D}_{1,j}^{{}}{{\mathbf{f}}_{1ux,\text{src}}}-\exp (-\text{j}{{k}_{cz,0}}\Delta z)\mathbf{D}_{1,j}^{2}{{\mathbf{f}}_{1sy,\text{src}}} \\ \end{matrix} \right) $ | (19) |
| $ \left( \begin{matrix} {{\mathbf{f}}_{1}} \\ {{\mathbf{f}}_{2}} \\ \end{matrix} \right)=\left( \begin{matrix} \exp (-\text{j}{{k}_{cz,0}}\Delta z)\mathbf{D}_{1,j}^{2}{{\mathbf{f}}_{1sy,\text{src}}} \\ -\mathbf{D}_{1,j}^{2}{{\mathbf{f}}_{1sy,\text{src}}} \\ \end{matrix} \right) $ | (20) |
块矩阵波动方程的左侧波动矩阵即为层吸收法所需建立3对角元矩阵,如式(22)所示。该块矩阵波动方程由逐网格波动方程组成,各网格波动方程来源于邻近两个网格的一阶差分旋度方程。这样的构造过程避免了层吸收法所需的矩阵重排序(Reordering)步骤,同时能直接的应用RCWA算法中微分波动方程的矩阵形式:
| $ {{\mathbf{A}}_{i}}=\mathbf{K}_{x}^{2}-\mathbf{E}_{i}^{{}} $ | (21) |
对于TM偏振入射平面衍射与二维光栅的衍射问题,直接应用收敛性改进研究方面的各类矩阵形式[9, 10],对改进层吸收法的收敛同样有效。

|
(22) |
对于TM偏振入射,其入射场可以表示为:
| $ {{H}_{\text{inc},y}}=\exp [-\text{j}{{k}_{0}}{{n}_{c}}(\sin \theta \cdot x+\cos \theta \cdot z)] $ | (23) |
类似TE偏振入射,可以最终写成如下的磁变量的块矩阵方程:

|
(24) |
式中,${{\mathbf{a}}_{i}}=\mathbf{D}_{i}^{2}$;${{\mathbf{b}}_{i}}=-2\mathbf{D}_{i}^{2}-\mathbf{E}_{\text{inv},i}^{-1}{{\mathbf{B}}_{i}}$;${{\mathbf{B}}_{i}}={{\mathbf{K}}_{x}}\mathbf{E}_{i}^{-1}{{\mathbf{K}}_{x}}-$$\mathbf{I}$;${{\mathbf{b}}_{-1}}={{\mathbf{Z}}_{\text{ref}}}\mathbf{D}_{1}^{2}-2\mathbf{D}_{1}^{2}-{{\mathbf{E}}_{c}}{{\mathbf{B}}_{c}}$;${{\mathbf{B}}_{c}}={{\mathbf{K}}_{x}}\mathbf{E}_{c}^{-1}{{\mathbf{K}}_{x}}-\mathbf{I};{{\mathbf{b}}_{0}}=-\mathbf{D}_{1}^{2}-\mathbf{D}_{1}^{2}{{\mathbf{E}}_{c}}\mathbf{E}_{\text{inv},1}^{{}}-{{\mathbf{E}}_{c}}{{\mathbf{B}}_{c}}$;${{\mathbf{b}}_{i,{{J}_{i}}}}=-\mathbf{D}_{i}^{2}-\mathbf{D}_{i+1}^{{}}\mathbf{D}_{i}^{{}}\times$ ${{\mathbf{a}}_{i,{{J}_{i}}}}=\mathbf{D}_{i+1}^{{}}\mathbf{D}_{i}^{{}}\mathbf{E}_{\text{inv},i}^{-1}\mathbf{E}_{\text{inv},i+1}^{{}}$;${{\mathbf{b}}_{I,{{J}_{I}}}}=$;$-\mathbf{D}_{I}^{2}-\mathbf{D}_{I}^{2}\mathbf{E}_{\text{inv},I}^{-1}\mathbf{E}_{\text{sub}}^{-1}-\mathbf{E}_{\text{inv},I}^{-1}\mathbf{B}_{I}^{{}}$;${{\mathbf{E}}_{\text{inv},i}}$为第i层的介电系数函数的倒数对应的托普利兹矩阵;$\mathbf{E}_{\text{inv},i}^{-1}$的应用来自于RCWA在TM偏振情况的收敛性改进表达式[12]。
式(24)给出的波动方程对应的全场/散射场模型与TE偏振入射有所区别,它的源Hinc,y应设置在覆盖层第-1网格处(${{\mathbf{{U}'}}_{-1}}$),如图 5所示,这样才能保证f1、f2可以对类似式(19)与式(20)这两种形式的源都适用。对于TM偏振入射,f1、f2为:
| $ \left( \begin{matrix} {{\mathbf{f}}_{1}} \\ {{\mathbf{f}}_{2}} \\ \end{matrix} \right)=\left( \begin{matrix} \exp (-\text{j}{{k}_{cz,0}}\Delta z)\mathbf{D}_{1}^{{}}{{\mathbf{E}}_{c}}{{\mathbf{f}}_{1sx,\text{src}}}+\mathbf{D}_{1,j}^{2}{{\mathbf{f}}_{1uy,\text{src}}} \\ -\mathbf{D}_{1}^{2}{{\mathbf{f}}_{1uy,\text{src}}} \\ \end{matrix} \right) $ | (25) |
| $ \left( \begin{matrix} {{\mathbf{f}}_{1}} \\ {{\mathbf{f}}_{2}} \\ \end{matrix} \right)=\left( \begin{matrix} \exp (-\text{j}{{k}_{cz,0}}\Delta z)\mathbf{D}_{1}^{2}{{\mathbf{E}}_{c}}{{\mathbf{f}}_{1uy,\text{src}}} \\ -\mathbf{D}_{1}^{2}{{\mathbf{f}}_{1uy,\text{src}}} \\ \end{matrix} \right) $ | (26) |
式中,f1uy, src的向量形式与TE偏振情况中f1sy, src一致,f1sx,src与TE偏振情况中f1ux,src一致。如果Hinc,y设置在覆盖层第0网格处,则只有式(23)适用。
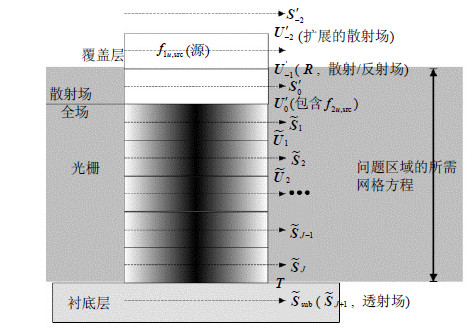 |
| 图5TM偏振平面衍射的全场/散射场模型 |
对于连续的3个网格方程(k-1、k、k+1),可以实现如下消元过程:
| $ \begin{matrix} \left. \begin{align} & {{\mathbf{a}}_{k-1}}{{\widetilde{\mathbf{S}}}_{k-2}}+{{\mathbf{b}}_{k-1}}{{\widetilde{\mathbf{S}}}_{k-1}}+{{\mathbf{c}}_{k-1}}{{\widetilde{\mathbf{S}}}_{k}}={{\widetilde{\mathbf{f}}}_{k-1}} \\ & {{\mathbf{a}}_{k}}{{\widetilde{\mathbf{S}}}_{k-1}}+{{\mathbf{b}}_{k}}{{\widetilde{\mathbf{S}}}_{k}}+{{\mathbf{c}}_{k}}{{\widetilde{\mathbf{S}}}_{k+1}}={{\widetilde{\mathbf{f}}}_{k}} \\ & {{\mathbf{a}}_{k+1}}{{\widetilde{\mathbf{S}}}_{k}}+{{\mathbf{b}}_{k+1}}{{\widetilde{\mathbf{S}}}_{k+1}}+{{\mathbf{c}}_{k+1}}{{\widetilde{\mathbf{S}}}_{k+2}}={{\widetilde{\mathbf{f}}}_{k+1}} \\ \end{align} \right\}\Rightarrow \\ \begin{matrix} \mathbf{a}_{k-1}^{{}}{{\widetilde{\mathbf{S}}}_{k-2}}+{{{\mathbf{{b}'}}}_{k-1}}{{\widetilde{\mathbf{S}}}_{k-1}}+{{{\mathbf{{c}'}}}_{k-1}}{{\widetilde{\mathbf{S}}}_{k+1}}={{\widetilde{{\mathbf{{f}'}}}}_{k-1}} \\ {{{\mathbf{{a}'}}}_{k+1}}{{\widetilde{\mathbf{S}}}_{k-1}}+{{{\mathbf{{b}'}}}_{k+1}}{{\widetilde{\mathbf{S}}}_{k+1}}+\mathbf{c}_{k+1}^{{}}{{\widetilde{\mathbf{S}}}_{k+2}}={{\widetilde{{\mathbf{{f}'}}}}_{k+1}} \\ \end{matrix} \\ \end{matrix} $ | (27) |
式中, $ \mathbf{{b}'}_{k-1}^{{}}=\mathbf{b}_{k-1}^{{}}-\mathbf{c}_{k-1}^{{}}\mathbf{b}_{k}^{-1}\mathbf{a}_{k}^{{}} $; $ \mathbf{{c}'}_{k-1}^{{}}=-\mathbf{c}_{k-1}^{{}}\mathbf{b}_{k}^{-1}{{\mathbf{c}}_{k}} $; $ {{\mathbf{{a}'}}_{k+1}}= $ $ -\mathbf{a}_{k+1}^{{}}\mathbf{b}_{k}^{-1}\mathbf{a}_{k}^{{}} $; $ {{\mathbf{{b}'}}_{k+1}}=\mathbf{b}_{k+1}^{{}}-\mathbf{a}_{k+1}^{{}}\mathbf{b}_{k}^{-1}{{\mathbf{c}}_{k}} $; $ {{\widetilde{\mathbf{f}}}^{\prime }}_{k-1}=\widetilde{\mathbf{f}}_{k-1}^{{}}- $ $ \mathbf{c}_{k-1}^{{}}\mathbf{b}_{k}^{-1}\widetilde{\mathbf{f}}_{k}^{{}} $; $ {{\widetilde{\mathbf{f}}}^{\prime }}_{k+1}=\widetilde{\mathbf{f}}_{k+1}^{{}}-\mathbf{a}_{k+1}^{{}}\mathbf{b}_{k}^{-1}\widetilde{\mathbf{f}}_{k}^{{}}$。
同时从式(22)、式(24)给出的矩阵方程形式,可以看出阶梯近似层内,如果网格数很多,则会存在大量的重复网格方程,从而可以层内采用串联倍速算法(cascading and doubling algorithm)[10]对其实现加速。反射场傅里叶系数向量 R可以通过如下方程得到:
| $ \left[ \begin{matrix} {{\beta }_{0}} & {{\alpha }_{0}} \\ {{\alpha }_{J}} & {{\beta }_{J}} \\ \end{matrix} \right]\left[ \begin{matrix} R \\ {{S}_{I,{{J}_{I}}}} \\ \end{matrix} \right]=\left[ \begin{matrix} f_{1}^{SAM} \\ f_{2}^{SAM} \\ \end{matrix} \right] $ | (28) |
| $ \begin{matrix} \mathbf{R}= \\ {{\left[ \mathbf{\beta }_{0}^{{}}-\mathbf{\alpha }_{0}^{{}}{{({{\mathbf{\beta }}_{J}})}^{-\mathbf{1}}}{{\mathbf{\alpha }}_{J}} \right]}^{-\mathbf{1}}}\left[ \mathbf{f}_{1}^{\text{SAM}}-\mathbf{\alpha }_{0}^{{}}{{({{\mathbf{\beta }}_{J}})}^{-\mathbf{1}}}\mathbf{f}_{2}^{\text{SAM}} \right] \\ \end{matrix} $ | (29) |
式中, $ \mathbf{\beta }_{0}^{{}} $、 $ \mathbf{\alpha }_{0}^{{}} $、 $ {{\mathbf{\alpha }}_{J}} $、${{\mathbf{\beta }}_{J}}$是对块矩阵波动方程完成所有层吸收消元后的系数矩阵。
3 数值示例根据傅里叶空间的层吸收法,计算一个如图 1所示垂直侧壁双介质光栅。
示例 1 垂直侧壁双介质光栅(如图 1所示)的衬底材料为硅,光栅的双介质材料为空气/硅(介质2),覆盖层为空气,周期为500 nm,光栅区域厚度为500 nm,介质2的占空比为0.5,入射角θ=10°,方位角为φ=0°,入射波长范围为190~1 000 nm。图 6为TE/TM偏振入射两种情况分别与RCWA结果比较的零级反射谱。本文的数值示例统一设以±12为计算的傅里叶展开截断阶次,数值收敛判定条件为均方差 $\sigma <10_{{}}^{-3}$。由图中可以看出,当数值结果稳定收敛时,傅里叶空间层吸收法在TE/TM偏振入射下的零级反射谱与RCWA结果完全吻合。示例1采用了串联倍速算法,网格数为194,计算时间几乎为RCWA的两倍。因此,对于垂直侧壁RCWA比SAM的计算效率更高;只有考虑RCWA所需阶梯近似层数与SAM所需光栅区域总网格数相差不大的结构,SAM才能实现衍射场的快速计算。
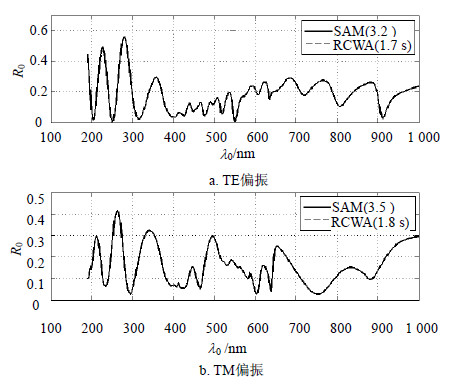 |
| 图6示例1在TE/TM偏振入射下,SAM与RCWA的零级反射谱曲线比较图 |
示例 2 双介质对称梯形光栅结构(其阶梯近似模型如图 2所示),光栅区域厚度为800 nm,梯形光栅的上下侧占空比分别为0.1、0.6,其余参数与示例1相同。在满足收敛条件($\sigma <10_{{}}^{-3}$,且最大绝对误差 $\delta <0.002$)下,SAM与RCWA的TE偏振入射零级反射谱比较如图 7所示。对于示例2,SAM需要划分157个网格,所需计算时间约为74.3 s;RCWA需要41个阶梯近似层,所需时间约为47.5 s。因此对于层厚较厚的光栅SAM的计算效率并不占优势。表 1给出了改变示例2厚度、占空比的其他梯形光栅(其余参数相同)的计算时间比较,收敛条件均为 $\sigma <10_{{}}^{-3}$且 $\delta <0.002$ 。可以看出,对于薄层且倾斜度( ${{f}_{2}}:{{f}_{1}}$)较大的结构SAM可能获得潜在的效率优势(阴影部分数据)。
 |
| 图7示例2在TE偏振入射下,SAM与RCWA的零级反射谱曲线比较图 |
示例3与示例2是相似的对称梯形光栅结构,但是其衬底材料为铬。图 8~图 10基于示例3给出了单独改变厚度、占空比( ${{f}_{1}}$、 ${{f}_{2}}$)、周期的3个几何参数所对应的两种算法计算时间曲线。可以看出厚度与占空比的改变对RCWA/SAM的相对计算效率影响较大。如图 8所示,对于倾斜度较大(f1=0.1, f2=0.8)的结构,厚度较小(小于380 nm)时,往往SAM更高效(d=140、160 nm时例外),其效率最高提升约40%,绝对计算时间最多减少约17s。如图 9所示,对于薄层(d=100nm)结构,保持f1=0.1时,f2越大SAM效率越高,但是保持f2=0.1、f1增加时,SAM相对于RCWA不具效率优势,因此倾斜度较大情况,RCWA/SAM的相对效率还需考虑光栅区域折射率分布的影响。特别的对于${{f}_{1}}$与${{f}_{2}}$接近的结构,RCWA效率极高,示例3在${{f}_{1}}$=${{f}_{2}}$=0.1时,不采用串联倍速算法的SAM需要约21 s,采用串联倍速算法的SAM需要约3 s,而RCWA仅需要约1.5 s,因此倾斜度较小结构,SAM不具效率优势。如图 10所示,对于示例3薄层倾斜度较大(d=100 nm, f1=0.1, f2=0.8)情况,周期对RCWA/SAM的相对计算效率影响较小,SAM效率最高提升约42%,绝对计算时间最多减少约14 s。相同计算平台上(本文数值结果均基于Inter E31280处理器/MKL代数库/Matlab数值软件)对于同等规模的问题(傅里叶展开截断为±12),RCWA/SAM的计算时间与阶梯近似层数/网格数满足如图 11所示的线性关系。因此相同收敛条件下对于该类光栅结构,如果SAM所需网格数小于RCWA所需阶梯近似层数的2倍左右,SAM更高(图 11中,trcwa(40)约需45.2 s,而tsam(80)约仅需37.2 s)。
| 表1 改变示例2厚度、占空比的RCWA与SAM的计算时间比较 |
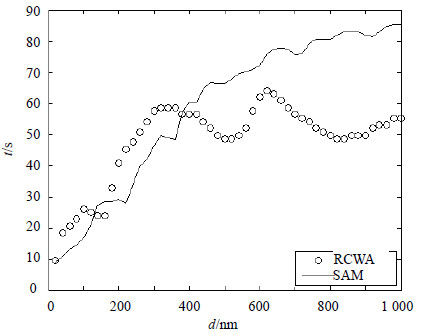 |
| 图8光栅厚度d对RCWA与SAM计算时间的影响 ( $\Lambda $=500 nm,f1=0.1,f2=0.8) |
 |
| 图9占空比(f1或f2)对RCWA与SAM计算时间的影响 (d=100 nm, $\Lambda $=500 nm) |
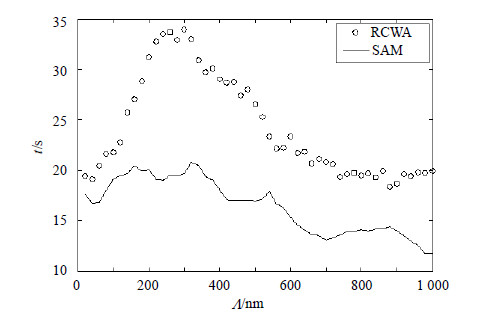 |
| 图10光栅周期 $\Lambda $对RCWA与SAM计算时间的影响 (d=100 nm,f1=0.1,f2=0.8) |
 |
| 图11RCWA/SAM的计算时间与阶梯近似层数/网格数的线性关系 |
以上示例说明,傅里叶空间的SAM在所需网格数小于RCWA所需阶梯近似层数的2倍左右的情况下,可以实现相对于RCWA的更高效计算,但其应用范围受到光栅几何参数、材料特性、入射光源综合影响。实际工程应用中,可以通过前期模拟分析判断特定结构下SAM与RCWA的相对效率,再选择合适的计算方式,最后实现集成电路结构的在线检测。此外,SAM避免了RCWA难以并行分解的特征值求解过程,因此相对于RCWA,它更适合应用于并行架构的高性能计算平台以进一步提高效率,如CPU-GPU架构服务器[13]。
4 结 论本文通过结合RCWA的傅里叶展开过程与层吸收法的差分迭代过程,可以实现对任意复杂形貌光栅零级衍射场的有效计算。对于在给定精度要求下,SAM所需网格数小于RCWA所需阶梯近似层数两倍左右的衍射模拟问题,SAM更高效。该方法完全适用于采用RCWA的各类波动矩阵形式(本文TM偏振平面衍射应用了 $E_{\text{inv},i}^{-1}$),以提高收敛性最终提高效率。本文的数值示例虽然只是典型结构的模拟计算,但是该方法对于任意复杂周期结构(包括二维结构)均具有实现相对于RCWA更高效计算的潜力。由于集成电路结构分析/测试应用中往往对实时性有较高要求,因此该方法具有一定的工程应用价值。傅里叶空间的SAM同样适用于类似文献[10]中的大规模的复杂光子晶体结构的分析设计。
| [1] | 樊叔伟,周庆华,李红. 槽型衍射光栅结构参数优化设计研究[J]. 光学学报,2010, 30(11): 3133-3139. FAN Shu-wei, ZHOU Qing-hua, LI Hong. Research of optimization design of groove diffraction grating profile parameters[J]. Acta Optica Sinica, 2010, 30(11): 3133-3139. |
| [2] | 周云,申溯,叶燕,等. 带有高折射率介质层的金属光栅偏振器特性的研究[J]. 光学学报,2010, 30(4): 1158-1161. ZHOU Yun, SHEN Su, YE Yan, et al. Research on characteristics of subwavelength metal grating polarizers with a high refractive-index dielectric layer[J]. Acta Optica Sinica, 2010, 30(4): 1158-1161. |
| [3] | 童凯,曾文智,谷朝聪,等. 覆层介质对光子晶体生物传感器灵敏度的影响[J]. 中国激光,2013, 40(2): 0214002-1-6. TONG Kai, ZENG Wen-zhi, GU Chao-cong, et al. Effects of coating on sensitivity of photonic crystal biosensor[J]. Chinese Journal of Lasers, 2013, 40(2): 0214002-1-6 |
| [4] | CHALYKH R, PUNDALEVA I, KIM S, et al. Simulation of critical dimension and profile metrology based on scatterometry method[C]//Proceeding SPIE 6349, Photomask Technology 2006. Bellingham: SPIE, 2006. |
| [5] | MOHARAM M G, GAYLORD T K. Rigorous coupled-wave analysis of planar-grating diffraction[J]. J Opt Soc Am, 1981, 71(7): 811-818. |
| [6] | MOHARAM M G, POMMET D A, GRANN E B, et al. Stable implementation of the rigorous coupled-wave analysis for surface-relief gratings: Enhanced transmittance matrix approach[J]. J Opt Soc Am A, 1995, 12(5): 1077-1086. |
| [7] | LI Li-feng. Formulation and comparison of two recursive matrix algorithms for modeling layered diffraction gratings [J]. J Opt Soc Am A, 1996, 13(5): 1024-1035. |
| [8] | POPOV E, NEVIERE M. Maxwell equations in Fourier space: Fast-converging formulation for diffraction by arbitrary shaped, periodic, anisotropic media[J]. J Opt Soc Am A, 2001, 18(11): 2886-2894. |
| [9] | EDEE K, PLUMEY J, GRANET G, et al. Perturbation method for the rigorous coupled wave analysis of grating diffraction[J]. Optics Express, 2010, 18(25): 26274-26284. |
| [10] | RUMPF R C, TAL A, KUEBLER S M. Rigorous electromagnetic analysis of volumetrically complex media using the slice absorption method[J]. J Opt Soc Am A, 2007, 24(10): 3123-3134. |
| [11] | MOHARAM M G, GRANN E B, POMMET D A. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings[J]. J Opt Soc Am A, 1995, 12(5): 1068-1076. |
| [12] | LI Li-feng. Use of Fourier series in the analysis of discontinuous periodic structures[J]. J Opt Soc Am A, 1996, 13(9): 1870-1876. |
| [13] | XIONG Qiang, CHEN Shu-qiang, HU Yan-fang. Efficient computation scheme of grating structure using RCWA and FDFD[C]//Computational Problem-solving(ICCP) 2011 International Conference. New York, USA: IEEE, 2011. |
 2015, Vol. 44
2015, Vol. 44
