2. 清华大学自动化系 北京 海淀区 100084
2. Department of Automation, Tsinghua University Haidian Beijing 100084
输入未知情况下的观测器设计是控制界学者广泛关注的问题之一。针对未知输入系统,文献[1, 2]给出了全维观测器的设计方法,文献[3, 4]给出了降维观测器设计方法,文献[5, 6]提出了滑模观测器,文献[7, 8]提出了自适应观测器。在许多工业系统中,未知输入可以是未知扰动或故障。因此,未知输入观测器在动态系统的故障检测领域有着广泛的应用[9, 10, 11, 12, 13]。
未知输入系统设计以上观测器的充分必要条件之一是系统满足未知输入和可测输出之间的秩条件(也称为观测器匹配条件)。但是,许多系统不满足匹配条件。最近,针对不满足匹配条件的系统,文献[14, 15, 16]提出了基于辅助输出的未知输入观测器设计方法。该方法通过引入辅助输出使得匹配条件得以满足,但是由于辅助输出不可测,所以需要用高增益近似微分器或者高阶滑模精确微分器进行估计,然后,使用这些估计值设计未知输入观测器,这使得观测器设计过程繁琐复杂。针对不满足匹配条件的系统,为了能够得到比较简单的观测器设计方法,文献[17]将未知输入分解成匹配未知输入和不匹配未知输入两部分,并假设不匹配部分可以表述为虚构的自治动态系统的响应。这样,可以得到一个同时包含原系统和不匹配未知输入建模系统的增广系统,使得匹配条件得以满足,然后设计降维观测器。
针对伴有未知输入的线性时不变系统,本文基于未知输入建模的思想,提出了一种在系统不满足观测器匹配条件的情况下Wolcott-Zak型滑模观测器的设计方法。相比于文献[17]的降维观测器,本文的方法有以下优点:1) 滑模观测器可以观测全状态,提高了设计的自由度和误差收敛速度;2) 可以利用滑模观测器中的输出注入信号重构未知输入。
1 系统描述和背景知识 1.1 系统描述本文考虑以下线性时不变系统:
| $\left\{ \begin{align} & \dot{x}=Ax+Bu+Dd \\ & y=Cx \\ \end{align} \right.$ | (1) |
系统(1)设计传统的未知输入观测器[1, 2, 3, 5, 6, 7, 8],必须满足以下条件:
1) $\{A,C,D\}$的不变零点位于复平面的左半开平面;2) $\text{rank}(D)=\text{rank}(CD)$。
当系统满足条件2)时,称系统(1)满足观测器匹配条件[18]。当系统满足观测器匹配条件时,文献[1, 2, 3, 5, 6, 7, 8, 9, 11, 13, 19, 20]提出了未知输入观测器设计方法。下面介绍一个关于设计Wolcott-Zak型滑模观测器的引理。
引理 1[19] 当系统同时满足条件1)和条件2)时,对于某些正定阵$Q\in {{R}^{n\times n}}$,存在矩阵$L\in {{R}^{n\times p}}$、$F\in {{R}^{q\times p}}$以及正定阵$P\in {{R}^{n\times n}}$,使得:
| $\left\{ \begin{array}{*{35}{l}} {{(A-LC)}^{\text{T}}}P+P(A-LC)=-Q \\ {{D}^{\text{T}}}\mathbf{P}=\mathbf{FC} \\ \end{array} \right.$ |
当系统(1)在满足条件1),但是不满足条件2)时,基于辅助输出的估计值,文献[14, 15]提出了滑模观测器设计方法,文献[3, 16]提出了降维观测器设计方法。但是,获得辅助输出估计值的过程比较复杂,文献[17]提出了一种简单易行的基于未知输入建模的降维观测器设计方法。本文希望当系统(1)在满足上述条件1),但是不满足条件2)的情况下设计Wolcott-Zak型滑模观测器,所以作出如下假设:
假设1 系统(1)满足条件1),但是不满足条件2),即$\text{rank}(D)\ne \text{rank}(CD)$。
当系统(1)同时满足条件1)和条件2)时,可以使用文献[6]中介绍的方法设计Wolcott-Zak型滑模观测器。本文希望基于对未知输入代数建模的方法,解决系统(1)不满足匹配条件的情况下设计Wolcott- Zak型滑模观测器的问题。
1.2 不匹配未知输入${{d}_{2}}$建模当系统(1)在不满足观测器匹配条件时,文献[17]将未知输入矩阵D分解成D1和D2,未知输入d分解成d1和d2,有:
| $D=[\begin{matrix} {{D}_{1}} & {{D}_{2}} \\ \end{matrix}],d=\left[ \begin{matrix} {{d}_{1}} \\ {{d}_{2}} \\ \end{matrix} \right]$ |
系统(1)可以描述为:
| $\left\{ \begin{align} & \dot{x}=Ax+Bu+{{D}_{1}}{{d}_{1}}+{{D}_{2}}{{d}_{2}} \\ & y=Cx \\ \end{align} \right.$ | (2) |
为了处理不匹配未知输入d2,作如下假设:
假设2 不匹配未知输入d2可以表述为自治动态系统的响应。
基于假设2,使用文献[21]中的代数建模方法,通过选择合适的矩阵${{E}_{2i}}\in {{R}^{{{\delta }_{i}}\times {{\delta }_{i}}}}$和${{H}_{2i}}\in {{R}^{1\times {{\delta }_{i}}}}$,得:
| $\left\{ \begin{align} & {{{\dot{z}}}_{2i}}={{E}_{2i}}{{z}_{2i}} \\ & {{d}_{2i}}={{H}_{2i}}{{z}_{2i}} \\ \end{align} \right.i=1,2,\cdots ,l-{{l}_{1}}$ | (3) |
| $\left\{ \begin{align} & {{{\dot{z}}}_{2}}={{E}_{2}}{{z}_{2}} \\ & {{d}_{2}}={{H}_{2}}{{z}_{2}} \\ \end{align} \right.$ | (4) |
| ${{E}_{2}}=\left[ \begin{matrix} {{E}_{21}} & {} & {} \\ {} & \ddots & {} \\ {} & {} & {{E}_{2\left( l-{{l}_{1}} \right)}} \\ \end{matrix} \right]$ |
| $\delta =\sum\limits_{i=1}^{l-{{l}_{1}}}{{{\delta }_{i}}}$ |
由系统方程(2)和未知输入模型(4)可得:
| $\left\{ \begin{align} & {{{\dot{x}}}_{a}}={{A}_{a}}{{x}_{a}}+{{B}_{a}}u+{{D}_{a}}{{d}_{1}} \\ & y={{C}_{a}}{{x}_{a}} \\ \end{align} \right.$ | (5) |
不难验证,有$\text{rank(}{{D}_{a}}\text{)}=\text{rank(}C{{D}_{a}}\text{)}={{l}_{1}}$成立,所以,增广系统(5)满足观测器匹配条件。
2 滑模观测器的设计本文希望系统(1)在不满足观测器匹配条件的情况下,可以设计Wolcott-Zak型滑模观测器。近来,文献[3, 14, 15, 16, 22]提出了观测器的设计方法,可以规避匹配条件的限制,但是,大都是基于辅助输出的估计值。在系统(1)不满足匹配条件的情况下,文献[17]设计了基于代数方法的降维观测器。本文的主要目的是当系统(1)不满足匹配条件时,基于代数建模方法设计Wolcott-Zak型滑模观测器,相比于文献[17]提出的降维观测器,具有设计自由度高、鲁棒性强等优点。
引理 2[17] 系统{A,B,C}的不变零点和$\left\{ {{A}_{a}},{{C}_{a}},{{D}_{a}} \right\}$的不变零点相同。
引理2表明,当假设1成立时,$\left\{ {{A}_{a}},{{C}_{a}},{{D}_{a}} \right\}$的不变零点依然位于复平面的左半开平面,再根据引理1,可得以下定理。
定理 1 对于某些正定阵${{Q}_{a}}\in {{R}^{(n+\delta )\times (n+\delta )}}$,存在矩阵${{L}_{a}}\in {{R}^{(n+\delta )\times p}}$ ${{F}_{a}}\in {{R}^{q\times p}}$以及正定阵${{P}_{a}}\in {{R}^{(n+\delta )\times (n+\delta )}}$,使得:
| $\left\{ \begin{array}{*{35}{l}} {{({{A}_{a}}-{{\mathbf{L}}_{a}}{{\mathbf{C}}_{a}})}^{\text{T}}}{{\mathbf{P}}_{a}}+{{\mathbf{P}}_{a}}({{\mathbf{A}}_{a}}-{{\mathbf{L}}_{a}}{{\mathbf{C}}_{a}}\text{)}=-{{\mathbf{Q}}_{a}} \\ \mathbf{D}_{a}^{\text{T}}{{\mathbf{P}}_{a}}={{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}} \\ \end{array} \right.$ | (6) |
定理1中的Lyapunov方程(6)成立是设计Wolcott-Zak型滑模观测器的充分必要条件,所以对系统(5),设计Wolcott-Zak型滑模观测器为:
| $\left\{ \begin{align} & {{{\dot{\hat{x}}}}_{a}}\text{ = }\mathbf{A}{{{\mathbf{\hat{x}}}}_{a}}\text{+ }{{\mathbf{B}}_{a}}\mathbf{u}+{{\mathbf{L}}_{a}}(\mathbf{y}-\mathbf{\hat{y}})+{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(\mathbf{y},\mathbf{\hat{y}},{{\eta }_{a}}) \\ & \mathbf{\hat{y}}={{\mathbf{C}}_{a}}{{{\mathbf{\hat{x}}}}_{a}} \\ & \mathbf{\hat{x}}=\left[ \begin{matrix} {{\mathbf{I}}_{n}} & {{0}_{n\times \delta }} \\ \end{matrix} \right]{{{\mathbf{\hat{x}}}}_{a}} \\ \end{align} \right.$ | (7) |
| ${{\mathbf{E}}_{a}}(\mathbf{y},\mathbf{\hat{y}},{{\eta }_{a}})=\left\{ \begin{matrix} {{\eta }_{a}}\frac{{{\mathbf{F}}_{a}}(\mathbf{y}-\mathbf{\hat{y}})}{\left\| {{\mathbf{F}}_{a}}(\mathbf{y}-\mathbf{\hat{y}}) \right\|} & {{\mathbf{F}}_{a}}(\mathbf{y}-\mathbf{\hat{y}})\ne 0 \\ 0 & {{\mathbf{F}}_{a}}(\mathbf{y}-\mathbf{\hat{y}})=0 \\ \end{matrix} \right.$ | (8) |
由式(5)和式(7)可得:
| ${{\mathbf{\dot{e}}}_{a}}=({{\mathbf{A}}_{a}}-{{\mathbf{L}}_{a}}{{\mathbf{C}}_{a}}){{\mathbf{e}}_{a}}+{{\mathbf{D}}_{a}}{{\mathbf{d}}_{1}}-{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(\mathbf{y},\mathbf{\hat{y}},{{\eta }_{a}})$ | (9) |
受文献[6]的启发,给出以下定理。
定理 2 基于假设1和假设2,当${{\eta }_{a}}>\rho $时,状态估计误差${{e}_{a}}$可以渐近跟踪系统(5)的状态。
证明:考虑Lyapunov方程$\mathbf{V}=\mathbf{e}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{e}}_{a}}$,沿误差方程(9)对v求导得:
| $\begin{align} & \mathbf{\dot{V}}=\mathbf{e}_{a}^{\text{T}}\left[ {{({{\mathbf{A}}_{a}}-{{\mathbf{L}}_{a}}{{\mathbf{C}}_{a}})}^{\text{T}}}{{\mathbf{P}}_{a}}+{{\mathbf{P}}_{a}}({{\mathbf{A}}_{a}}-{{\mathbf{L}}_{a}}{{\mathbf{C}}_{a}}) \right]{{\mathbf{e}}_{a}}+ \\ & 2\mathbf{e}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{d}}_{1}}-2\mathbf{e}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(\mathbf{y},\mathbf{\hat{y}},{{\eta }_{a}}) \\ \end{align}$ |
由式(6)的第1个方程,可得:
| $\mathbf{\dot{V}}=-\mathbf{e}_{a}^{\text{T}}{{\mathbf{Q}}_{a}}{{\mathbf{e}}_{a}}+2\mathbf{e}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{d}}_{1}}-2\mathbf{e}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(\mathbf{y},\mathbf{\hat{y}},{{\eta }_{a}})$ | (10) |
由式(6)的第2个方程,有:
| $2\mathbf{e}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{d}}_{1}}\le 2\left\| {{\mathbf{d}}_{1}} \right\|\left\| \mathbf{D}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{e}}_{a}} \right\|\le 2\rho \left\| {{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{e}}_{a}} \right\|$ | (11) |
由式(6)的第2个方程和式(8),有:
| $\begin{align} & 2\mathbf{e}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(\mathbf{y},\mathbf{\hat{y}},{{\eta }_{a}})=2{{\eta }_{a}}\frac{\mathbf{e}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{e}}_{a}}}{\left\| {{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{e}}_{a}} \right\|}= \\ & 2{{\eta }_{a}}\frac{{{({{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{e}}_{a}})}^{\text{T}}}(\mathbf{D}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{e}}_{a}})}{\left\| {{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{e}}_{a}} \right\|}\le 2{{\eta }_{a}}\left\| {{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{e}}_{a}} \right\| \\ \end{align}$ | (12) |
将式(11)和式(12)代入式(10),可得:
| $\mathbf{\dot{V}}=-\mathbf{e}_{a}^{\text{T}}{{\mathbf{Q}}_{a}}{{\mathbf{e}}_{a}}-2({{\eta }_{a}}-2\rho )\left\| {{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{e}}_{a}} \right\|$ |
为了减轻滑模过程中的抖振现象,通常在实际操作过程中,使用以下滑模控制率:
| ${{E}_{a}}(y,\hat{y},{{\eta }_{a}})=\left\{ \begin{matrix} {{\eta }_{a}}\frac{{{\mathbf{F}}_{a}}(y-\hat{y})}{\left\| {{\mathbf{F}}_{a}}(y-\hat{y}) \right\|+{{\varepsilon }_{1}}} & {{\mathbf{F}}_{a}}(y-\hat{y})\ne 0 \\ 0 & {{\mathbf{F}}_{a}}(y-\hat{y})=0 \\ \end{matrix} \right.$ | (13) |
式中,${{\varepsilon }_{1}}>0$。
由文献[6]可知,可以在有限时间里到达滑模面$\left\{ {{e}_{a}}:\sigma ={{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{e}}_{a}}=0 \right\}$,且在状态误差空间里保持不变,从而有:
| $\begin{align} & \dot{\sigma }={{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}({{\mathbf{A}}_{a}}-{{\mathbf{L}}_{a}}{{\mathbf{C}}_{a}}){{\mathbf{e}}_{a}}+{{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{d}}_{1}}- \\ & {{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(y,\hat{y},{{\eta }_{a}})=0 \\ \end{align}$ | (14) |
| ${{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{d}}_{1}}={{\mathbf{F}}_{a}}{{\mathbf{C}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(y,\hat{y},{{\eta }_{a}})$ | (15) |
| $\mathbf{D}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{d}}_{1}}=\mathbf{D}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(y,\hat{y},{{\eta }_{a}})$ | (16) |
| ${{\mathbf{d}}_{1}}=\mathbf{D}_{a}^{\text{T}}{{\mathbf{P}}_{a}}{{\mathbf{D}}_{a}}{{\mathbf{E}}_{a}}(y,\hat{y},{{\eta }_{a}})t\to \infty $ | (17) |
当系统(1)不满足匹配条件时,基于未知输入建模的方法,文献[17]给出了一种降维观测器的设计,本文则给出了Wolcott-Zak型滑模观测器的设计。可以看出,滑模观测器式(7)和式(8)不仅可以渐近跟踪系统的状态,还可以重构部分未知输入信号,弥补了文献[17]方法的不足。
3 仿真将本文提出的Wolcott-Zak型滑模观测器设计方法用于如下由直流电机驱动的一个机械手链接环节的标称模型[17],有:
| $\left\{ \begin{align} & {{{\dot{\theta }}}_{m}}={{\omega }_{m}} \\ & {{{\dot{\omega }}}_{m}}=\frac{{{k}_{t}}}{{{J}_{m}}}({{\theta }_{l}}-{{\theta }_{m}})-\frac{{{B}_{r}}}{{{J}_{m}}}{{\omega }_{m}}+\frac{{{K}_{\tau }}}{{{J}_{m}}}u \\ & {{{\dot{\theta }}}_{l}}={{\omega }_{l}} \\ & {{{\dot{\omega }}}_{l}}=\frac{{{k}_{t}}}{{{J}_{l}}}({{\theta }_{l}}-{{\theta }_{m}})-\frac{{{m}_{p}}gh}{{{J}_{l}}}\sin {{\theta }_{l}} \\ \end{align} \right.$ |
| $\left\{ \begin{align} & \mathbf{\dot{x}}=\mathbf{Ax}+\mathbf{Bu}+\mathbf{\Phi }\text{(}\mathbf{x})+\mathbf{\Delta }\xi \\ & \mathbf{y}=\mathbf{Cx} \\ \end{align} \right.$ |
| $\begin{align} & \mathbf{x}=\left[ \begin{matrix} {{\theta }_{m}} \\ {{\omega }_{m}} \\ {{\theta }_{l}} \\ {{\omega }_{l}} \\ \end{matrix} \right];A=\left[ \begin{matrix} 0 & 1 & 0 & 0 \\ -48.6 & -1.25 & 48.6 & 0 \\ 0 & 0 & 0 & 1 \\ 1.95 & 0 & -1.95 & 0 \\ \end{matrix} \right] \\ & B=\left[ \begin{matrix} 0 \\ 21.6 \\ 0 \\ 0 \\ \end{matrix} \right];\Phi \text{(}x\text{)}=\left[ \begin{matrix} 0 \\ 0 \\ 0 \\ -3.333\sin {{\theta }_{l}} \\ \end{matrix} \right];\Delta =\left[ \begin{matrix} 1 \\ 0 \\ 1 \\ 1 \\ \end{matrix} \right]; \\ & C=\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ \end{matrix} \right] \\ \end{align}$ |
非线性项$\Phi (x)$可以表示为$\Phi (x)=Rv$,其中,$R={{[\begin{matrix} 0 & 0 & 0 & -0.333 \\ \end{matrix}]}^{\text{T}}}$。则原系统可以重写为:
| $\left\{ \begin{align} & \mathbf{\dot{x}}=\mathbf{Ax}+\mathbf{Bu}+\mathbf{Dd} \\ & \mathbf{y}=\mathbf{Cx} \\ \end{align} \right.$ |
容易验证$\text{rank(}CD\text{)}\ne \text{rank(}D\text{)}$,则传统的滑模观测器设计方法将不再适用。因为$\text{rank(}\mathbf{C\Delta }\text{)}=\text{rank(}\Delta \text{)}=1$,$CE=0$,所以可取${{d}_{1}}=\xi ,{{D}_{1}}=\Delta ,{{d}_{2}}=v,{{D}_{2}}=R$,从而有$\text{rank(}C{{D}_{1}}\text{)}=\text{rank(}{{D}_{1}}\text{)}=1$。假设${{d}_{2}}$为正弦信号,由文献[21]可得:
| ${{E}_{2}}=\left[ \begin{matrix} 0 & 1 \\ -{{(2\pi )}^{2}} & 0 \\ \end{matrix} \right],{{H}_{2}}=[\begin{matrix} 1 & 0 \\ \end{matrix}]$ |
| $\begin{align} & {{F}_{a}}={{10}^{8}}\times [\begin{matrix} 0.994\ 2 & -0.013\ 1 & 1.543\ 4 \\ \end{matrix}] \\ & {{L}_{a}}=\left[ \begin{matrix} 0.949\ 8 & -2.157\,\,1 & 1.127\ 9 \\ -17.066\ \,1 & 5.539\ 2 & 24.479\ 5 \\ 0.071\,\ 8 & 1.543\ 5 & 0.901\ 2 \\ 1.735\ 3 & -1.010\ 2 & 1.314\ 4 \\ -0.977\ 7 & 0.266\ 6 & 1.250\ 2 \\ -4.136\ 3 & 10.292\ 8 & -1.085\ 7 \\ \end{matrix} \right] \\ \end{align}$ |
增广系统的状态和滑模观测器的状态初始值分别设为$x(0)={{[\begin{matrix} -10 & -1 & -1 & -3 \\ \end{matrix}]}^{T}}$,${{\hat{x}}_{a}}(0)={{[\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \\ \end{matrix}]}^{\text{T}}}$。系统不确定性为$\xi =0.25\sin (6\text{ }\!\!\pi\!\!\text{ }t)$。
3.1 仿真结果图 1~图 4给出了系统状态及其观测值,图 5给出了系统的匹配未知输入d1及其重构值。从仿真结果可以看出,本文的Wolcott-Zak型滑模观测器可以很好地跟踪原系统的状态和重构未知扰动信号。
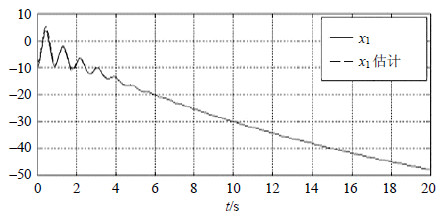 |
| 图1 ${{x}_{1}}$及其估计 |
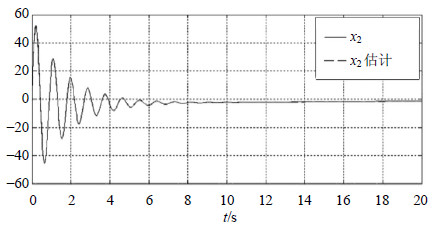 |
| 图2 ${{x}_{2}}$及其估计 |
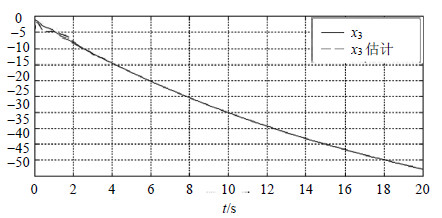 |
| 图3 ${{x}_{3}}$及其估计 |
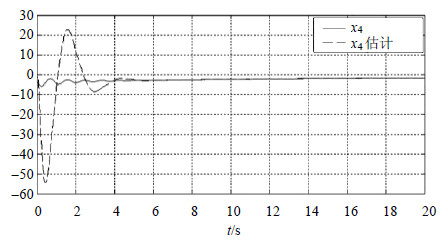 |
| 图4 ${{x}_{4}}$及其估计 |
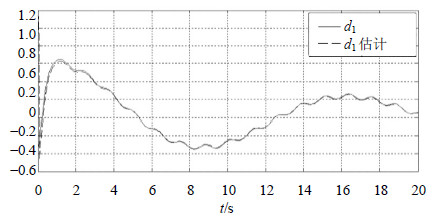 |
| 图5 ${{x}_{5}}$及其估计 |
本文针对一类线性时不变系统,在观测器匹配条件不满足的情况下,探讨了Wolcott-Zak型滑模观测器的设计。基于对未知输入的代数建模方法,得到一类满足匹配条件的增广系统,并证明可以对该增广系统设计Wolcott-Zak型滑模观测器。将本文方法应用于一类柔性机器人系统,从仿真结果可以看出该方法是有效的。
| [1] | CHEN J, PATTON R J. Robust model-based fault diagnosis for dynamic systems[M]. MA, USA: Kluwer Academic Publishers Norwell, 1999. |
| [2] | YANG F, WILDE R W. Observers for linear systems with unknown inputs[J]. IEEE Transactions on Automatic Control, 1988, 33(7): 677-681. |
| [3] | ZHU F. State estimation and unknown input reconstruction via both reduced-order and high-order sliding mode observers[J]. Journal of Process Control, 2012, 1(22): 296-302. |
| [4] | HOU M, MÜLLER P C. Design of observers for linear systems with unknown inputs[J]. IEEE Trans Automatic Control, 1992, 37(6): 871-875. |
| [5] | EDWARDS C, SPURGEON S K, PATTON R J. Sliding mode observers for fault detection and isolation[J]. Automatica, 2000, 36(4): 541-553. |
| [6] | HUI S, ZAK S H. Observer design for systems with unknown inputs[J]. International Journal of Applied Mathematics and Computer Science, 2005, 15(4): 431-446. |
| [7] | WANG H, DALEY S. Actuator fault diagnosis: an adaptive observer-based technique[J]. IEEE Trans on Automatic Control, 1996, 41(7): 1073-1078. |
| [8] | ZHANG K, JIANG B. Vincent cocquempot, adaptive observer-based fast fault estimation[J]. International Journal of Control, Automation, and Systems, 2008, 6(3): 320-326. |
| [9] | TAN C P, EDWARDS C. Sliding mode observers for robust detection and reconstruction of actuator send sensor faults[J]. International Journal of Robust and Nonlinear Control, 2003, 13(5): 443-443. |
| [10] | FLOQUET T, BARBOT J P, PERRUQUETTI W, et al. On the robust fault detection via a sliding mode observer[J]. International Journal of Control, 2004, 77(7): 622-629. |
| [11] | WANG J L, YANG G H, LIU J. An LMI approach to H- index and mixed H-/H∞ fault detection observer design[J]. Automatica, 2007, 43(9): 1656-1665. |
| [12] | NG K Y, TAN C P, OETOMO D. Disturbance decoupled fault reconstruction using cascaded sliding mode observers[J]. Automatica, 2012, 48(5): 794-799. |
| [13] | MAO Ze-hui, JIANG Bin, SHI Peng. Fault-tolerant control for a class of nonlinear sampled-data systems via a Euler approximate observer[J]. Automatica, 2010, 46(5): 1852-1859. |
| [14] | FLOQUET T, EDWARDS C, SPURGEON S K. On sliding mode observers for systems with unknown inputs[J]. International Journal of Adaptive Control and Signal Processing, 2007(21): 638-656. |
| [15] | KALSI K, LIAN J, HUI S, et al. Sliding-mode observers for systems with unknown inputs: a high-gain approach[J]. Automaitca, 2010, 46(2): 347-353. |
| [16] | 韩冬, 朱芳来. 基于辅助输出的线性系统状态和未知输入同时估计方法[J]. 自动化学报, 2012, 38(6): 932-943. HAN Dong, ZHU Fang-lai. Simultaneous estimation of states and unknown inputs for linear systems based on auxiliary outputs[J]. Acta Automatica Sinica, 2012, 38(6): 932-943. |
| [17] | PARK T G. Designing fault detection observers for linear systems with mismatched unknown inputs[J]. Journal of Process Control, 2013, 23(8): 1185-1196. |
| [18] | DRAZENOVIC B. The invariance conditions in variable structure systems[J]. Automatica, 1969, 5(3): 287-295. |
| [19] | CORLESS M, TU J. State and input estimation for a class of uncertain systems[J]. Automatica, 1998, 34(6): 757-764. |
| [20] | ZHANG K, JIANG B, SHI P. Fast fault estimation and accommodation for dynamical systems[J]. IET Cont Theor Appl, 2009, 3(2): 189-199. |
| [21] | ALBERTOS P, SALA A. Multivariable control systems: an engineering approach[M]. London: Springer, 2004. |
| [22] | 项基, 苏宏业, 褚健. 一类不确定系统的滑模观测器设计[J]. 控制理论与应用, 2006, 23(6): 996-1000. XIANG Ji, SU Hong-ye, CHU Jian. Sliding-mode observer design for a class of uncertain system[J]. Control Theory and Applications, 2006, 23(6): 996-1000. |
 2015, Vol. 44
2015, Vol. 44
