2. School of Electronic Engineering, University of California-Los Angeles Los Angeles Califonia USA 90034
布尔网络的稳定状态包括两种:不动点和环。不动点是环的一种特例,即环步长为1。布尔网络环的计算是一个NP完全问题[1, 2]。近年来,随着布尔满足性判定SAT算法的不断优化,越来越多的布尔网络问题都可以用SAT算法求解,如无边界的符号模式检测、可达性分析、量词消除、基因调控网络求环等[3, 4, 5, 6, 7, 8],但对于复杂布尔网络的所有环的求解仍然具有非常高的计算复杂度。本文的目标是基于SAT全解算法计算所有小于指定步长的环。
1 相关技术 1.1 基本术语使用SAT算法求解,绝大部分应用都需要转换成通用的SAT问题描述形式,即CNF范式。CNF范式由所有子句的合取形式构成,其中每个子句是若干文字(变量或非变量)的析取。每个文字是变量本身或者是变量的非。CNF范式的格式为:
| $F=\underset{i=1}{\overset{N}{\mathop{\wedge }}}\,{{C}_{i}},{{C}_{i}}={{l}_{1}}\vee {{l}_{2}}\vee \cdots \vee {{l}_{k}}$ | (1) |
Davis-Putnam-Longeman-Loveland(DPLL)算法是完全SAT求解算法的基本架构。几乎它是所有现代的完全求解算法的基础,包括单文字子句消除、肯定-否定规则、原子公式消除等boolean constraint propagation(BCP)规则。而CDCL和非时序回退的技术能够有效的降低搜索空间,进而降低SAT算法的时间和空间复杂度[9]。
BCP算法实现子句单元广播,即根据已赋值的变量推导未赋值的变量值。如果BCP推导时出现冲突,则调用CDCL算法进行冲突学习并生成冲突子句。冲突子句可以避免重复的路径搜索。CDCL算法基于蕴含图(implication graph)技术实现冲突子句的学习和非时序的决策级回退。蕴含图描述在搜索过程中的部分变量赋值及蕴含关系,选择不同的决策变量选择和不同的BCP顺序将生成不同的蕴含图,因此搜索过程中蕴含图是动态变化的。
1.3 基于单解求解器的全解求解算法计算满足性判定问题F的所有满足解,可以基于单解求解器通过如下步骤实现:
1) 判断F是否满足。若不满足,则输出不满足;否则,计算一个满足解${{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}}$,n是问题中的变量数。
2) 用vi表示满足解中的一个变量赋值。若解xi,则对应的变量表示为$\neg {{v}_{i}}$;否则表示为vi。因此,一个满足解可以表示为由变量或变量的非形成的一个合取子句s。
3) 将满足解形成的合取子句取反,即所有变量取反并形成一个析取子句c。
4) 将析取子句c加入到求解的问题集F,形成新的问题集$F=F\wedge c$。
5) 判断新的问题集F'是否存在满足解。若存在,则转到步骤2);否则输出所有已计算的满足解。
上述求全解的过程存在如下问题:
1) 每一次满足解的计算都是以整个问题为基础,对前一次求解过程中的搜索空间没有记录。
2) 没有根据求全解的特点进行搜索算法优化。
针对上述问题,文献[3]提出了阻塞子句(blocking clause)的方式。当单解SAT求解器获得一个满足解时,并不停止求解过程,而是将该满足解对应的变量合取表示方式取反形成一个析取子句作为阻塞子句加到问题集中,继续求解过程。通过这种方式可以保留前一次求解过程中所学习的冲突子句,并不再搜索已经搜索过的路径空间。然而,由于满足性问题的满足解可能非常多,从而导致阻塞子句需要较大的内存空间,并且大量的阻塞子句也会增加问题的求解复杂度。文献[4]为降低阻塞子句的数量,使用子句聚合方式对产生的阻塞子句集进行蕴含化简,缩短阻塞子句的长度,进而降低阻塞子句的数量。文献[10]提出了基于算法避免再次获得重复满足解的方式,降低内存开销并保持求解复杂度不变。它没有使用阻塞子句的方式避免计算重复解,而是基于决策变量与求得解的蕴含关系生成冲突子句,进而避免后续的计算出现重复的解。这种生成冲突子句的方式在本质上等同于生成阻塞子句的方式。同时,它提出了求解问题中变量划分的方法,它将要求解问题中的变量划分成两类:重要变量集和不重要变量集。在搜索过程中先选择重要变量进行决策赋值,当重要变量全部赋值完成后才对不重要变量进行决策赋值。然而该算法是基于CNF范式的求解,其重要变量和非重要变量没有结合具体问题进行定义。文献[11]为降低阻塞子句的数量并降低后续计算的搜索空间使用最短阻塞子句的方式计算全解,它基于覆盖算法最小化满足片段减少阻塞子句中的文字数,但该算法使用的覆盖算法本身复杂度也比较高,对于问题子句数和变量数多的求解问题计算复杂度较大。
上述求全解算法只考虑了如何避免已求得的满足解的问题,而计算不动点、基因调控网络吸引区求解等问题在计算过程中不能仅避免已求得的满足解,还需要避免已经计算的不动点或状态环。
2 布尔网络环求解算法 2.1 基于状态转换函数和环属性创建求解问题布尔网络描述的是变量之间的相互依赖关系,每个变量的值只能是0或1。变量的下一个时刻的值由依赖节点的当前时刻的值确定,即:
| ${{{v}'}_{i}}={{f}_{i}}({{v}_{1}},{{v}_{2}},\cdots ,{{v}_{m}})$ | (2) |
式中,${{{v}'}_{i}}$表示节点i的下一个时刻的状态值;v1,${{v}_{2}},\cdots ,{{v}_{m}}$,表示节点i依赖的m个节点的当前时刻的值。
布尔网络的环是布尔网络状态转换过程中的稳定状态。如果环的步长为N,则布尔网络至少需要经过N个时刻的状态迁移才能进入环状态。因此,根据布尔网络的状态转换函数,可以通过N步展开的方式生成包含N+1个布尔网络状态的转换路径,即:
| $\text{path}=\underset{k=1}{\overset{N}{\mathop{\wedge }}}\,{{T}_{k}}({{s}_{k-1}},{{s}_{k}})$ | (3) |
同时,步长小于等于N的所有环的属性p可以描述成为:
| $p=\underset{k=0}{\overset{N}{\mathop{\vee }}}\,({{s}_{N}}={{s}_{N-k}})$ | (4) |
根据式(2)~式(4)可以得到计算步长小于等于N的环的求解问题集,并可以通过引入辅助变量的方式将其转换成CNF形式。
2.2 基于SAT全解算法的环计算基于阻塞子句、冲突蕴含图生成阻塞子句和变量分类等SAT全解算法的实现技术,结合布尔网络转换关系和环属性描述方式,本文提出了求解步长小于等于N的环的求解算法。其算法的基本流程为:
Input: CNF范式F,变量集V,环步长N;
Output:全部满足解all-solution或不满足UNSAT;
初始化:
L=NULL; //L是确定赋值的文字集合;
DecisionLevel = 0; //DecisionLevel是搜索的深度;
Status = SAT;
生成CNF问题集F:
$F=\text{transtoCNF}((\underset{i=1}{\overset{N}{\mathop{\wedge }}}\,T({{s}_{i-1}},{{s}_{i}}))\wedge (\underset{k=0}{\overset{N}{\mathop{\vee }}}\,({{s}_{N}}={{s}_{N-k}})))$setDecisionVars(F);
IF (BCP(F,L)==CONFLICT) THEN Return UNSAT;
WHILE (Status == SAT)
Begin
preClauseCount =F; //获得原始问题的子句数量;
WHILE (sizeof(L) < sizeof(V)) //sizeof()获得变量的数量;
Begin
l=PickBranchLit(F,V\Var(L)); //从未赋值的变量中选择一个变量赋值,Var(L)是已赋值的变量集合;
Add(l, L); DecisionLevel++; //增加赋值变量到解集L;
IF (BCP(F, L) == CONFLICT)
Begin
DecisionLevel = CDCL(F, L);
If (DecisionLevel < curDecisionLevel)
Begin
removeClausesFrom(preClauseCount);
c=GenBlockClause(D);
$F=F\wedge c$;
End
IF (DecisionLevel==0) Status = UNSAT, Break;
ELSE BackJump(DecisionLevel);
End
End
curDecisionLevel = DecisionLevel;
s =L;//获得一个满足解;
c=GenBlockClause(D);
$F=F\wedge c$;
BackJump(DecisionLevel - 1);
End
IF (Sizeof(All-Solution) > 0) Return All-Solution;
ELSE Return UNSAT;
PickBranchLit()函数实现决策变量的选择并为其赋值。根据转换CNF过程中存在大量辅助变量的特性,选择决策变量时采用了变量分类的方式减少决策变量的选择空间。setDecisionVars()函数用于设置变量的属性,即该变量是否可以作为决策变量。GenBlockClause()函数根据当前的决策变量赋值获得阻塞子句。参数D表示决策级为k时的所有决策变量赋值对应的文字集合$D=\{{{d}_{1}},{{d}_{2}},\cdots ,{{d}_{k}}\}$,则GenBlockClause()函数生成的阻塞子句为c=$\neg {{d}_{1}}\vee \neg {{d}_{2}}\vee \cdots \vee \neg {{d}_{k}}$。
2.3 基于变量分类的决策文字选择优化为提高搜索速度并降低搜索空间,本文将待选择变量分为两类:决策变量和蕴含变量。决策变量是布尔网络状态转换过程中对应的状态变量,蕴含变量是布尔网络转换成CNF范式过程中引入的辅助变量。本文中布尔网络的描述形式采用的是类似于berkeley logic interchange format (BLIF)的格式,转换关系示例如表 1所示。
| 表1 布尔网络转换关系描述示例 |
表 1能够准确的描述布尔网络节点之间的依赖关系,并根据该依赖关系得到对应的布尔网络状态转换函数。在同步布尔网络中,给定一个布尔网络的转换步数N后,可以根据转换关系展开得到布尔网络的状态转换图,并将其转换成CNF形式。然而在转换过程中将会引入大量的辅助变量。表 1中的每一个转换定义项都需要引入一个辅助变量。下面以表 1中节点2的下一个状态转换函数为例描述转换过程:
1)若节点的当前状态为1,则表示为${{v}_{i}}(i\in \{1,2,3\})$,否则表示为$\neg {{v}_{i}}$。
2)若节点的下一个状态为1,则表示为${{{v}'}_{i}}(i\in \{1,2,3\})$,否则表示为$\neg {{{v}'}_{i}}$。
3) 根据表 1中(.n 2 2 1 3)的描述,其转换函数${{{v}'}_{2}}=f({{v}_{1}},{{v}_{3}})$,同时其后的两行分别表示${{{v}'}_{2}}=\neg {{v}_{1}}\wedge {{v}_{3}}=1$和${{{v}'}_{2}}={{v}_{1}}\wedge \neg {{v}_{3}}=1$,即节点2的转换关系函数可表示为:
| ${{{v}'}_{2}}=(\neg {{v}_{1}}\wedge {{v}_{3}})\vee ({{v}_{1}}\wedge \neg {{v}_{3}})$ | (5) |
4) 针对转换关系函数中的每一个合取项引入一个辅助变量${{y}_{1}},{{y}_{2}}$,并令${{y}_{1}}=\neg {{v}_{1}}\wedge {{v}_{3}},{{y}_{2}}={{v}_{1}}\wedge \neg {{v}_{3}}$,则节点2的转换关系函数可表示为:
| ${{{v}'}_{3}}=({{y}_{1}}=\neg {{v}_{1}}\wedge {{v}_{3}})\wedge ({{y}_{2}}={{v}_{1}}\wedge \neg {{v}_{3}})\wedge ({{v}_{2}}'={{y}_{1}}\vee {{y}_{2}})$ | (6) |
5)步骤4)的转换关系转换成CNF范式的子句集为:
| $\begin{align} & {{{{v}'}}_{4}}=(\neg {{y}_{1}}\vee \neg {{v}_{1}})\wedge (\neg {{y}_{1}}\vee {{v}_{3}})\wedge ({{y}_{1}}\vee {{v}_{1}}\vee \neg {{v}_{3}})\wedge \\ & (\neg {{y}_{2}}\vee {{v}_{1}})\wedge (\neg {{y}_{2}}\vee \neg {{v}_{3}})\wedge ({{y}_{2}}\vee \neg {{v}_{1}}\vee {{v}_{3}})\wedge \\ & (\neg {{y}_{1}}\vee {{{{v}'}}_{2}})\wedge (\neg {{y}_{2}}\vee {{{{v}'}}_{2}})\wedge ({{y}_{1}}\vee {{y}_{2}}\vee \neg {{{{v}'}}_{2}}) \\ \end{align}$ | (7) |
根据上述转换过程可以看出,辅助变量的赋值是由节点状态值所蕴含的,因此在SAT求解过程中只要确定了节点状态值,则辅助变量的赋值能够根据蕴含关系确定,因此在PickBranchLit()函数选择决策变量的过程中不需要选择辅助变量作为决策变量,进而降低SAT求解的搜索空间。
2.4 基于蕴含图的决策变量生成阻塞子句优化根据计算全解和增加子句的过程,可将要求解的问题分成两部分:原始的问题F和阻塞子句集B。
SAT问题F的一个满足解${{s}_{i}}({{x}_{1}},{{x}_{2}},\cdots ,{{x}_{n}})$可以用合取子句${{c}_{i}}={{l}_{1}}\wedge {{l}_{2}}\wedge \cdots \wedge {{l}_{n}}$表示,如果${{x}_{i}}=1$,则子句中对应的文字${{l}_{i}}={{v}_{i}}$;否则${{l}_{i}}=\neg {{v}_{i}}$。因此,所有已获得的m个满足解的集合将形成一个析取disjunctive normal form(DNF)范式,其格式为:
| $S=\underset{i=1}{\overset{m}{\mathop{\vee }}}\,{{c}_{i}}$ | (8) |
基于满足解集,可以得到阻塞子句集$B=\neg S$。在计算是否存在$m+1$个满足解时,需要将F加入到问题集$F=F\wedge B$中,即$F=F\wedge B$,以避免获得重复的解。显然,$S$中包含的子句越多且每个子句中的文字数越多,则计算$m+1$个满足解的时间和空间复杂度越大。
优化的目标之一是降低阻塞子句中文字的数量。冲突子句学习的SAT求解算法会在求解过程中基于选择的决策变量进行蕴含推理,进而生成局部蕴含图。蕴含图示例如图 1所示。
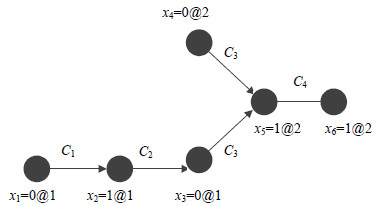 |
| 图1 SAT求解过程中的蕴含图示例 |
图 1中待求解的CNF范式由4个子句构成$F={{C}_{1}}\wedge {{C}_{2}}\wedge {{C}_{3}}\wedge {{C}_{4}}$。${{x}_{i}}=al$表示决策级为l时xi的值为a。子句数据库为${{C}_{1}}={{x}_{1}}\vee {{x}_{2}}$,${{C}_{2}}=\neg {{x}_{2}}\vee \neg {{x}_{3}}$,${{C}_{3}}={{x}_{3}}\vee {{x}_{4}}\vee {{x}_{5}}$,${{C}_{4}}=\neg {{x}_{5}}\vee {{x}_{6}}$。决策级为1时,决策变量及分配的值为{x1=0@1},蕴含分配的值为{x2=1@1, x3=0@1}。决策级为2,决策变量及分配的值为{x4=0@2},蕴含分配的值为{x5=1, x6=1}。最后获得可满足解{x1=0, x2=1,x3=0, x4=0, x5=1, x6=1}。
根据图 1可以看到,当前的可满足解$s=\{\neg {{v}_{1}},{{v}_{2}},\neg {{v}_{3}},\neg {{v}_{4}},{{v}_{5}},{{v}_{6}}\}$是由两个决策变量的赋值$d=\{{{x}_{1}}=01,{{x}_{4}}=02\}$确定的。因此,为避免下一次计算出现重复的解,则生成的阻塞子句是$\neg {{v}_{1}}\wedge \neg {{v}_{4}}$的非,即${{v}_{1}}\vee {{v}_{4}}$。显然,使用决策变量生成阻塞子句的方式极大的降低了阻塞子句中文字的数量。
优化目标之二是减少阻塞子句的数量。在基于冲突子句的SAT求解过程中,当获得一个满足解时,采用时序回退的算法计算下一个满足解。即全解搜索方式采用深度优先搜索算法。在深度优先搜索时,如果冲突回退的决策级比当前的决策级小,则表明当前决策级之下已经不存在满足解,则可以删除当前产生的所有阻塞子句,并基于回退的决策级backlevel生成一个阻塞子句$c=\neg {{d}_{1}}\vee \neg {{d}_{2}}\vee \cdots $ $\vee \neg {{d}_{\text{backlevel}}}$,表示backlevel之后的所有满足解都已经被计算,并使用一个阻塞子句c避免所有搜索过的满足解空间。
3 实验结果分析基于Minisat求解器[12]实现了不动点和步长小于等于K的周期性环的SAT全解算法period cycles algorithm based on decision node and important variable(PC-DI)。并选择了一个基于SAT计算所有环的求解器BNS[5]作为比较工具。实验使用与文献[5]的测试案例和N-K随机布尔网络作为测试基准。N-K网络使用R环境中的BoolNet包随机生成8个最大环长不超过100的布尔网络。测试平台的配置为Intel Xeon CPU@3.3 GHz 8-Core(测试时只用了一个核),内存为128 GB,操作系统是Ubuntu 12.04。
实验分析了两方面的性能:所有周期性环求解性能和指定步长周期性环求解性能。
为了使用本文的算法计算所有的周期环,首先使用BNS计算出所有环并获得最大的环长,然后以最大环长为指定步长运行本文的求解器,测试结果如表 2所示。
| 表2 所有环求解计算结果 |
实验结果显示本文算法在计算环的最大步长小于100的真实案例和随机案例中都具有较大的性能优势。
基于表 2的测试结果,选择其中4个BNS计算时间在100s以上的案例(Random2, Random4, Random6, Random8)进行指定步长环计算的分析。对每一个测试案例指定不同的步长进行测试。指定的步长初始值为1,每次增加4个步长,最大指定步长设置为69(大于所有测试案例的环的最大步长)。测试结果如图 2和图 3所示。
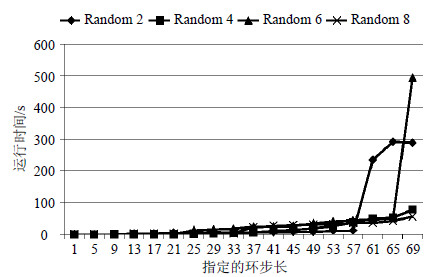 |
| 图2 指定步长环的运行时结果 |
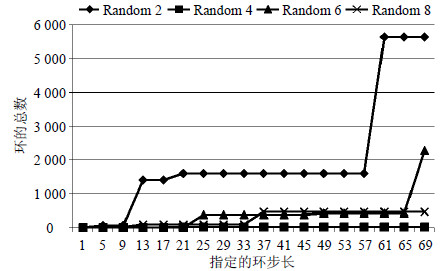 |
| 图3 小于等于指定步长环的总环数 |
图 2比较的是指定最大环步长时计算所有周期环的时间,图 3比较的是指定最大环步长时计算出的周期环的数量。Random2、Random4、Random6和Random8的所有周期环分别是5632个、24个、2280个和478个。图 2显示Random4和Random8的运行时间增加比较平缓,Random2和Random6分别在指定步长为61和69时运行时间增加较大。结合图 3可以看出,Random2和Random6分别在指定步长为61和69时周期性环数显著增加。
实验结果显示,本文算法对于环长分布比较均匀的布尔网络具有较低的计算复杂度,并且指定的步长与运行时间成线性增加的关系。同时,对于运行时间较长且环长分布不均匀的案例(步长大的环占所有环的比例较高),其主要的时间开销集中在步长大的周期环计算过程中。
基于实验结果可以看到,当指定的步长小于最大状态环步长时,算法计算复杂度较低。因此本文算法可以通过指定步长的方式求解更复杂的布尔网络的状态环。对于无法在有限的时间内计算所有周期环的案例,本文将具有更大的优势。
4 结束语本文提出了一种高效的周期性状态环求解算法。为降低决策变量的选择空间提升搜索速度,该算法将布尔网络转换成CNF过程中引入的辅助变量标记为非决策变量。通过引入基于蕴含图技术建立阻塞子句的方式,该算法能够降低阻塞子句的数量并实现非时序题集的方式,可以充分利用SAT全解求解算法计算状态环。实验结果表明,该算法具有较低的计算复杂度,并且能够对复杂的网络进行指定步长的状态环求解。
| [1] | ZHAO Q. A remark on "scalar equations for synchronous boolean networks with biological applications" by C. Farrow, J. Heidel, J. Maloney, and J. Rogers[J]. IEEE Transactions on Neural Networks, 2005, 16(6): 1715-1716. |
| [2] | T AKUTSU, S KOSUB, A A MELKMAN, et al. Finding a periodic attractor of a Boolean network[J]. Transactions on Computational Biology and Bioinformatics, 2012, 9(5): 1410-1421. |
| [3] | MCMILLAN K L. Applying SAT methods in unbounded symbolic model checking[C]//14th International Conference on Computer Aided Verification. Denmark: Springer, 2002. |
| [4] | CHAUHAN P, CLARKE E M, KROENING D. Using SAT based image computation for reachability analysis[M]. The Netherlands: Springer, 2003. |
| [5] | DUBROVA E, TESLENKO M. A SAT-based algorithm for finding attractors in synchronous Boolean networks[J]. Transactions on Computational Biology and Bioinformatics (TCBB), 2011, 8(5): 1393-1399. |
| [6] | ZHENG De-sheng, YANG Guo-wu, LI Xiao-yu, et al. An efficient algorithm for computing attractors of synchronous and asynchronous Boolean networks[EB/OL].[2014-01-01] http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0060593. |
| [7] | GUO W, YANG G, WU W, et al. A parallel attractor finding algorithm based on Boolean satisfiability for genetic regulatory networks[EB/OL].[2014-01-03] http://journals.plos.org/plosone/article?id=10.1371/journal.pone.0094258. |
| [8] | BRAUER J, KING A, KRIENER J. Existential quantification as incremental SAT[C]//23rd International Conference on Computer Aided Verification. Snowbird UT, USA: Springer, 2011. |
| [9] | LIMA J F. Boolean satisfiability solvers: Techniques, implementations and analysis[J]. Electrónica e Telecomunicações S. A., 2013, 5(2): 218-225. |
| [10] | GRUMBERG O, SCHUSTER A, YADGAR A. Memory efficient all-solutions SAT solver and its application for reachability analysis[C]//5th international confrence on Formal Methods in Computer-Aided Design. Texas, USA: Springer, 2004. |
| [11] | YU Y, SUBRAMANYAN P, TSISKARIDZE N, MALIK S. All-SAT using minimal blocking clauses[C]//27th International Conference on VLSI Design and 13th International Conference on Embedded Systems. Mumbai, India: IEEE, 2014. |
| [12] | EEN N, SORENSSON N. Minisat 2.2.0[CP/DK].[2014-02-02]. http://minisat.se/downloads/minisat-2.2.0.tar.gz . |
 2015, Vol. 44
2015, Vol. 44
