多标签数据在现实世界中广泛存在。与传统的单标签数据不同,多标签数据可以同时包含多个标签。例如一张图片中存在房屋、树木、湖泊等多个景物,每类景物作为一个标签可以为这张图片贴上多个标签。每个标签可以作为一个单独的类别,因此,多标签数据可以同时被划分到多个类别中,且比单标签数据分类更为复杂。
早期有关多标签数据分类的研究主要集中在文本数据方面[1, 2]。近十年来,随着图像检索、数据挖掘、标签推荐等方面的发展,多标签学习逐渐成为一个热门的研究方向。目前,研究者们已提出了一些有效的多标签学习算法。如文献[3]提出的ML-KNN算法将传统的k-近邻算法和贝叶斯理论相结合,来实现多标签数据的分类;文献[4]联合多个分类器,提出一套针对多标签数据分类的整体方案,成功地对音乐流派进行多标签分类;文献[5]提出基于核的多标签分类算法Rank-SVM,实现了对基因数据集的有效分类。
另一方面,稀疏表示与压缩感知[6]也受到广泛重视。其中,文献[7]利用训练样本稀疏线性表示待测试样本,提出稀疏表示分类方法(SRC),实现了高效并且鲁棒的人脸识别;文献[8]对稀疏系数加入非负性约束,将非负稀疏表示分类(non-negative SRC, NSRC)应用于人脸识别;文献[9]采用近邻数据进行稀疏线性重构,提出基于稀疏近邻表示的分类(sparse neighbor representation dassification, SNRC)方法。文献[10]将SRC算法应用于多标签数据分类,提出基于稀疏表示的多标记学习算法(ML-SRC)。
ML-SRC算法首先利用全部训练样本在LASSO[11]稀疏最小化约束下线性表示待测试样本,然后对稀疏系数的元素进行筛选,大于0的稀疏系数所对应的训练样本被认为与待测试样本有正相关而被保留下来,小于0的系数被直接置0;最后,通过计算待测试样本对于每个标签类别的隶属度来实现多标签分类。然而,该算法用全部训练数据组成字典,给后面稀疏系数的计算带来巨大的计算量,并且当训练数据中存在非线性流形结构时,所得到的稀疏重构及分类效果会受到严重影响。此外,将小于0的稀疏系数强制改为0,丢弃了稀疏系数中的所有负数,仅保留非负稀疏系数进行多标签分类,导致稀疏重构系数中判别信息的严重丢失,从而使得分类效果下降。
本文针对上述两个现象,提出一种非负稀疏近邻表示的多标签学习算法(ML-NSNRC)。
1 相关方法 1.1 基于稀疏表示的多标签数据分类假设训练集包含n个多标签训练样本${{\mathbf{y}}_{i}}\in {{R}^{d}}$,$i=1,2,\cdots ,n\mathbf{T}=\{1,2,\cdots ,L\}$为其所对应的标签集合。所有训练样本拼成矩阵形式$\mathbf{D}=[{{\mathbf{y}}_{1}},{{\mathbf{y}}_{2}},\cdots ,{{\mathbf{y}}_{n}}]\in {{R}^{d\times n}}d < n$。根据训练样本包含的标签信息,构造训练样本${{\mathbf{y}}_{i}}$的标签信息${{\mathbf{b}}_{i}}$,若${{\mathbf{y}}_{i}}$包含标签l,则令${{b}_{li}}=1$,否则令${{b}_{li}}=0$。构造训练样本矩阵D对应的标签矩阵$\mathbf{B}=[{{b}_{1}},{{b}_{2}},\cdots ,{{b}_{n}}]\in {{R}^{L\times n}}$。多标签学习的目标是学习一个多标签分类器$h:\mathbf{y}\to {{2}^{L}}$,来对待测试样本y所包含的标签进行估计。ML-SRC利用训练集D稀疏线性重构待测试样本y:
| $\underset{{}}{\mathop{\mathbf{\hat{s}}=\arg \underset{\mathbf{s}}{\mathop{\min }}\,}}\,\frac{1}{2}||\mathbf{y}-\mathbf{Ds}||_{2}^{2}+\lambda ||\mathbf{s}|{{|}_{1}}$ | (1) |
式中,s表示稀疏线性重构系数;$\lambda >0$为调节参数。
ML-SRC[10]算法采用函数$f(\mathbf{y},l)$来计算待测试样本属于每个标签的隶属度:
| $f(\mathbf{y},l)={\sum\limits_{i=1}^{n}{({{b}_{li}}}\overset{{}}{\mathop{{{{\hat{s}}}_{i}})}}\,}/{\sum\limits_{i=1}^{n}{{{{\hat{s}}}_{i}}}}\;\text{ }l=1,2,\cdots ,L$ | (2) |
式中,${\hat s_i} = \left\{ {\begin{array}{*{20}{c}} {{s_i}{\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {s_i} > 0} \\ {0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {s_i} \leqslant 0} \end{array}} \right.,{\kern 1pt} i = 1,2, \cdots ,n$。通过对$f(\mathbf{y},l)$与阈值函数的比较,得到y的预测标签集$h(\mathbf{y})$。
1.2 稀疏近邻表示分类算法稀疏近邻表示分类算法(SNRC)[9]在训练集中先找到待测试样本在每个类别上的k-近邻,然后用每个类别的k-近邻样本数据对待测试样本进行稀疏线性重构,并根据其在每个类别上k-近邻的重构误差最小对待测试样本分类。
SNRC通过优化目标函数${{\mathbf{s}}_{\mathbf{i}}}$得到待测试样本y的稀疏线性重构系数:
| ${{\mathbf{s}}_{\mathbf{i}}} = \mathop {\operatorname{argmin} }\limits_{{{\mathbf{s}}_i}} ||{\mathbf{y}} - {{\mathbf{\psi }}_{\mathbf{i}}}{{\mathbf{s}}_{\mathbf{i}}}|{|_2} + \lambda ||{{\mathbf{s}}_{\mathbf{i}}}|{|_1}$ | (3) |
式中,${{\mathbf{\psi }}_{\mathbf{i}}}$表示待测试样本y在训练样本集D的第i类训练样本上的k-近邻样本集合;$i = 1,2, \cdots ,c$;c表示训练样本集中的类别总数;调节参数$\lambda > 0$。根据每个类别的重构误差最小对待测试样本进行分类。SNRC采用近邻数据进行稀疏线性重构,可有效地避免训练数据中非线性流形结构带来的影响。
2 非负稀疏近邻分类借鉴SNRC采用近邻数据进行稀疏线性重构,可有效地避免训练数据中非线性流形结构给稀疏线性重构带来的影响。同时借鉴非负稀疏表示分类[8]在优化过程中直接限制其稀疏系数为非负,可使待测试样本用局部近邻数据进行凸的稀疏线性重构。由此,本文提出非负稀疏近邻分类(NSNRC)方法。
2.1 NSNRC目标函数NSNRC算法通过KNN方法得到待测试样本y在训练样本集D的第i类上的k-近邻样本集${{\mathbf{\psi }}_{\mathbf{i}}}$。将${{\mathbf{\psi }}_{\mathbf{i}}}$作为基,对稀疏系数加入非负约束,得到待测试样本y在${{\mathbf{\psi }}_{\mathbf{i}}}$上的非负稀疏解:
| $\begin{gathered} {{{\mathbf{\hat s}}}_i} = \arg \mathop {\min }\limits_{{{\mathbf{s}}_i}} \frac{1}{2}||{\mathbf{y}} - {{\mathbf{\psi }}_i}{{\mathbf{s}}_i}||_2^2 + \lambda ||{{\mathbf{s}}_i}|{|_1}{\kern 1pt} \\ {\text{s}}{\text{.t}}{\text{.}}{\kern 1pt} {\kern 1pt} \;\;i = 1,2, \cdots ,c \\ \end{gathered} $ | (4) |
式中,${\kern 1pt} {\kern 1pt} |{\mathbf{|}}{{\mathbf{s}}_i}|{|_1} = \sum\limits_{j = 1}^k {|{s_i}_j} |,_{}^{}{s_i}_j \geqslant 0$,$j = 1,2, \cdots k;\lambda > 0$。
当训练样本集D存在非线性流形时,${{\mathbf{\psi }}_{\mathbf{i}}}$可看成符合局部线性流形的训练样本子集。加入非负性限制后,对局部近邻数据点进行凸性重构,进一步挖掘局部结构信息,从而提高重构效果。
2.2 NSNRC的优化算法由于NSNRC的目标函数式(4)是一个凸函数,因此可以证明存在全局最优解。一般,全局最优解可通过二次规划或梯度下降得到。然而,梯度下降收敛较慢,二次规划实施又比较复杂,因此采用类似文献[12]提出的乘法迭代更新公式来求式(4)中的最优非负稀疏重构系数:
| ${{\mathbf{s}}_{i}}{{^{(}}^{t+1)}}={{\mathbf{s}}_{i}}^{(t)}{}^{{{\mathbf{\psi }}_{i}}^{\text{ }\!\!T\!\!\text{ }}\mathbf{y}}\!\!\diagup\!\!{}_{({{\mathbf{\psi }}_{i}}^{\text{ }\!\!T\!\!\text{ }}{{\mathbf{\psi }}_{i}}{{\mathbf{s}}_{i}}^{(t)}+\lambda 1)}\; $ | (5) |
式中,1表示一个全为1的向量。当${{\mathbf{s}}_i}$中每个初始元素全部为正时,${{\mathbf{s}}_i}$中的元素在式(5)更新下的结果均是非负的。
2.3 算法收敛性分析本文利用辅助函数对NSNRC的优化算法进行收敛性分析。
定义 1 若$G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)})$是$F({{\mathbf{s}}_i})$的辅助函数,则需要满足以下条件:
| $G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)}) \geqslant F({{\mathbf{s}}_i}),G({{\mathbf{s}}_i},{{\mathbf{s}}_i}) = F({{\mathbf{s}}_i})$ | (6) |
引理 1 如果${\mathbf{K}}({{\mathbf{s}}_i}^{(t)})$是对角矩阵:
| ${{\mathbf{K}}_{ab}}({{\mathbf{s}}_i}^{(t)}) = {\delta _{ab}}\frac{{{{({{\mathbf{\psi }}^{\text{T}}}{\mathbf{\psi }}{{\mathbf{s}}_i}^{(t)})}_a} + \lambda }}{{{{\mathbf{s}}_i}_a^{(t)}}}$ | (7) |
那么$F({{\mathbf{s}}_i})$的辅助函数可定义为:
| $\begin{gathered} G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)}) = F({{\mathbf{s}}_i}^{(t)}) + ({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)})\nabla F({{\mathbf{s}}_i}^{(t)}) + \\ \frac{1}{2}{({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)})^{\text{{\rm T}}}}K({{\mathbf{s}}_i}^{(t)})({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)}) \\ \end{gathered} $ | (8) |
引理1证明:显然$G({{\mathbf{s}}_i},{{\mathbf{s}}_i}) = F({{\mathbf{s}}_i})$成立,只需要证明$G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)}) \geqslant F({{\mathbf{s}}_i})$。其中:
| $\begin{gathered} F({{\mathbf{s}}_i}) = F({{\mathbf{s}}_i}^{(t)}) + ({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)})\nabla F({{\mathbf{s}}_i}^{(t)}) + \\ \frac{1}{2}{({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)})^{\text{{\rm T}}}}({{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }})({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)}) \\ \end{gathered} $ | (9) |
与式(8)比较,结果为:
| $0 \leqslant {({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)})^{\text{{\rm T}}}}[{\mathbf{K}}({{\mathbf{s}}_i}^{(t)}) - {{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }}]({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)})$ | (10) |
为了证明式(10)的半正定性,只需考虑矩阵:
| ${{\mathbf{M}}_{ab}}({{\mathbf{s}}_i}^{(t)}) = {{\mathbf{s}}_i}_a^{(t)}{({\mathbf{K}}({{\mathbf{s}}_i}^{(t)}) - {{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }})_{ab}}{{\mathbf{s}}_i}_b^{(t)}$ | (11) |
的半正定性。当且仅当${\mathbf{M}}$半正定时,${\mathbf{K}} - {{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }}$也为半正定:
| $\begin{gathered} {x^{\text{{\rm T}}}}{\mathbf{M}}x = \sum\limits_{ab} {{x_a}{{\mathbf{M}}_{ab}}} {x_b} = \\ \sum\limits_{ab} {{{\mathbf{s}}_i}_a^{(t)}{{({{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }})}_{ab}}} {{\mathbf{s}}_i}_b^{(t)}x_a^2 - {x_a}{{\mathbf{s}}_i}_a^{(t)}{({{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }})_{ab}}{{\mathbf{s}}_i}_b^{(t)}{x_b} + \lambda = \\ \sum\limits_{ab} {{{({{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }})}_{ab}}} {{\mathbf{s}}_i}_a^{(t)}{{\mathbf{s}}_i}_b^{(t)}\left[ {\frac{1}{2}x_a^2 + \frac{1}{2}x_b^2 - {x_a}{x_b}} \right] + \lambda = \\ \frac{1}{2}\sum\limits_{ab} {{{({{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }})}_{ab}}} {{\mathbf{s}}_i}_a^{(t)}{{\mathbf{s}}_i}_b^{(t)}{({x_a} - {x_b})^2} + \lambda \geqslant 0 \\ \end{gathered} $ | (12) |
式(12)中证明了M的半正定性,由此可知式(10)也是半正定的,进而可知$G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)}) \geqslant F({{\mathbf{s}}_i})$,因此引理1成立。
引理 2 如果G是一个辅助函数,那么目标函数F在以下更新中是非增的
| ${{\mathbf{s}}_i}^{(t + 1)} = \arg \mathop {\min }\limits_{{{\mathbf{s}}_i}} G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)})$ | (13) |
引理2证明:由式(13)易知$G({{\mathbf{s}}_i}^{(t + 1)},{{\mathbf{s}}_i}^{(t)}) \leqslant G({{\mathbf{s}}_i}^{(t)},{{\mathbf{s}}_i}^{(t)})$,又由引理1可知当$G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)})$是$F({\mathbf{s}})$的辅助函数时,满足定义1中的条件。因此有如下结果:
| $F({{\mathbf{s}}_i}^{(t + 1)}) \leqslant G({{\mathbf{s}}_i}^{(t + 1)},{{\mathbf{s}}_i}^{(t)}) \leqslant G({{\mathbf{s}}_i}^{(t)},{{\mathbf{s}}_i}^{(t)}) = F({{\mathbf{s}}_i}^{(t)})$ | (14) |
则引理2成立。
由引理2可知,当且仅当${{\mathbf{s}}_i}^{(t)}$的值使$G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)})$达到局部最小时,$F({{\mathbf{s}}_i}^{(t + 1)}) = F({{\mathbf{s}}_i}^{(t)})$。当$F({{\mathbf{s}}_i})$在${{\mathbf{s}}_i}^{(t)}$的邻域内导数存在且连续时,通过迭代式(13)可得到目标函数的一串有顺序的估计值,当目标函数到达局部最小值时,估计值收敛:
| $F({{\mathbf{s}}_i}_{\min }) \leqslant F({{\mathbf{s}}_i}^{(t + 1)}) \leqslant F({{\mathbf{s}}_i}^{(t)}) \leqslant \cdots \leqslant F({{\mathbf{s}}_i}^{_0})$ | (15) |
根据引理2,利用梯度下降使辅助函数的导数为0,推导稀疏系数的更新规则:
| $\begin{gathered} {\nabla _{{{\mathbf{s}}_i}}}G({{\mathbf{s}}_i},{{\mathbf{s}}_i}^{(t)}) = \\ {{\mathbf{\psi }}^{\text{{\rm T}}}}({\mathbf{\psi }}{{\mathbf{s}}_i}^{(t)} - {\mathbf{y}}) + \lambda {\mathbf{1}} + {\mathbf{K}}({{\mathbf{s}}_i}^{(t)})({{\mathbf{s}}_i} - {{\mathbf{s}}_i}^{(t)}) = 0 \\ \end{gathered} $ | (16) |
解得:
| $\begin{gathered} {{\mathbf{s}}_i} = {{\mathbf{s}}_i}^{(t)} - {k^{ - 1}}({{\mathbf{s}}_i}^{(t)})({{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }}{{\mathbf{s}}_i}^{(t)} - {{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{y}} + \lambda {\mathbf{1}}) = \hfill \\ {{\mathbf{s}}_i}^{(t)} - ({{\mathbf{s}}_i}^{(t)}/({{\mathbf{\psi }}^{\text{T}}}{\mathbf{\psi }}{{\mathbf{s}}_i}^{(t)}) + \lambda {\mathbf{1}})({{\mathbf{\psi }}^{\text{T}}}{\mathbf{\psi }}{{\mathbf{s}}_i}^{(t)} - {{\mathbf{\psi }}^{\text{T}}}{\mathbf{y}} + \lambda {\mathbf{1}}) = \hfill \\ {{\mathbf{s}}_i}^{(t)}({{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{y}})/({{\mathbf{\psi }}^{\text{{\rm T}}}}{\mathbf{\psi }}{{\mathbf{s}}_i}^{(t)} + \lambda {\mathbf{1}}) \hfill \\ \end{gathered} $ | (17) |
因此,非负稀疏近邻分类方法的目标函数可通过迭代优化算法式(5)来求解。
2.4 算法复杂度分析本文提出的NSNRC算法计算复杂度可通过分析式得到。式(5)中${({{\mathbf{\psi }}_i})^{\text{ T}}}{\mathbf{y}}$和${({{\mathbf{\psi }}_i})^{\text{ T}}}{{\mathbf{\psi }}_i}$的计算复杂度分别为${ O}(kd)$和${\rm O}({k^2}d)$,其中,d为数据维数,k为待测试样本y的近邻数。优化算法每一步的计算复杂度为${ O}(2k + {k^2} + k)$。因此,NSNRC的计算复杂度为$O(kd + {k^2}d + t(3k + {k^2}))$,其中,t为优化迭代次数。采用快速迭代收缩门限算法(fast iterative shrinkage-thresholding algorithm, FISTA)方法对SRC算法求其稀疏解,根据文献[13]可得其计算复杂度为$O(t{n^2}d)$,其中,n为训练样本集D的样本总数。
3 基于非负稀疏近邻表示的多标签分类虽然基于稀疏表示的多标签分类方法可以达到不错的分类效果,但仍存在以下不足:1) 在求解标签隶属度时,ML-SRC对稀疏解中的负值进行的置0操作势必导致稀疏解包含的判别信息严重丢失,从而对多标签分类的结果造成一定影响;2) ML- SRC在所有训练数据集上对待测试样本进行稀疏表示。当训练数据集中存在非线性流形时,如果仍在所有训练数据上进行稀疏表示则会产生严重影响。本文提出的非负稀疏近邻分类方法可有效解决以上两个不足。
令待测试样本y在训练集D上各标签的k-近邻集${\mathbf{\Psi }} = [{\mathbf{\varphi }}_1^0,{\mathbf{\varphi }}_1^1,{\mathbf{\varphi }}_2^0,{\mathbf{\varphi }}_2^1, \cdots ,{\mathbf{\varphi }}_L^0,{\mathbf{\varphi }}_L^1] \in {R^{d \times 2kL}}$,其中,d为样本的维度,k为近邻数,L为数据集标签总数。${\mathbf{\varphi }}_l^j$由KNN方法求得,表示待测试样本y在D中第l标签的第j类上的k-近邻,其中,上标j=0表示不存在标签l的类别,j=1表示存在标签l的类别。
将${\mathbf{\varphi }}_l^j$作为基,对稀疏系数加入非负约束,得到待测试样本y在${\mathbf{\varphi }}_l^j$上的非负稀疏解:
| $\begin{matrix} \mathbf{\hat{s}}_{\mathbf{l}}^{\mathbf{j}}=\arg \underset{s_{l}^{j}}{\mathop{\min }}\,\frac{1}{2}||\mathbf{y}-\mathbf{\varphi }_{l}^{j}\mathbf{s}_{\mathbf{l}}^{\mathbf{j}}||_{2}^{2}+\lambda ||\mathbf{s}_{\mathbf{l}}^{\mathbf{j}}|{{|}_{1}} \\ \operatorname{s}.t.s{{_{l}^{j}}_{i}}\ge 0,i=1,2,\cdots ,k,j=0,1,\ \ l=1,2,\cdots ,L \\ \end{matrix}$ | (18) |
式中,$||{\mathbf{s}}_{\mathbf{l}}^{\mathbf{j}}|{|_1} = \sum\limits_{i = 1}^k {|s_{li}^j|} $;调节参数$\lambda > 0$。
根据NSNRC的优化算法,得到最优非负稀疏重构系数的优化迭代公式:
| $\mathbf{s}{{_{\mathbf{l}}^{\mathbf{j}}}^{(}}^{t+1)}=\mathbf{s}{{_{\mathbf{l}}^{\mathbf{j}}}^{(t)}}{({{(\mathbf{\varphi }_{l}^{j})}^{\text{ }\!\!T\!\!\text{ }}}\mathbf{y})}/{({{(\mathbf{\varphi }_{l}^{j})}^{\text{ }\!\!T\!\!\text{ }}}\mathbf{\varphi }_{l}^{j}\mathbf{s}{{_{\mathbf{l}}^{\mathbf{j}}}^{(t)}}+\lambda 1)}\;$ | (19) |
式中,${\kern 1pt} {\kern 1pt} t \geqslant 0$。
根据所求得的非负稀疏解来计算待测试样本y对每个标签类别的重构误差:
| $\varepsilon _l^j(x) = ||{\mathbf{\varphi }}_l^j{\mathbf{s}}_{\mathbf{l}}^{\mathbf{j}} - {\mathbf{y}}|{|_2}$ | (20) |
根据y对应各标签上每类的重构误差,提出一个实值函数$g({\mathbf{y}},l)$来表示待测试样本y属于标签l的隶属度:
| $g({\mathbf{y}},l) = \frac{{{e^{ - \varepsilon _l^1({\mathbf{y}})}}}}{{{e^{ - \varepsilon _l^0({\mathbf{y}})}} + {e^{ - \varepsilon _l^1({\mathbf{y}})}}}}$ | (21) |
根据求得的隶属度预测待测试样本y的标签集$h({\mathbf{y}}) = \{ l|g({\mathbf{y}},l) > p({\mathbf{y}}),l \in {\mathbf{T}}\} $,其中,$p({\mathbf{y}})$为阈值函数。
3.2 ML-NSNRC的算法流程在ML-NSNRC算法中,待测试样本y被其在训练集中各标签的每一类上的k-近邻集稀疏重构。再通过稀疏重构误差来计算待测试样本y属于每个标签类的隶属度进而确定y的标签集。算法流程为:
1) 输入,训练样本矩阵${\mathbf{D}} = [{{\mathbf{y}}_1},{{\mathbf{y}}_2}, \cdots ,{{\mathbf{y}}_n}] \in {R^{d \times n}}$及其对应的标签集信息${\mathbf{B}} \in {R^{L \times n}}$,待测试样本${\mathbf{y}} \in {R^d}$;
2) 输出,待测试样本y的隶属度$g({\mathbf{y}},l)$和标签集。
分为以下3个步骤:
1) 利用${\ell _1}$范数对D中每一列归一化,通过KNN方法得到待测试样本y在训练集中各标签的每一类上的K-近邻集,从而得到${\mathbf{\Psi }}$;
2) 利用式(20)求待测试样本y在${\mathbf{\varphi }}_l^j$上的非负稀疏解${\mathbf{s}}_{\mathbf{l}}^{\mathbf{j}}$,${\mathbf{s}}_{\mathbf{l}}^{\mathbf{j}}$初始值设为1/n;
3) 根据求得的非负稀疏系数,利用式(20)和式(21)计算待测试样本属于每个标签的隶属度,进而确定y的标签集。
4 实验分析 4.1 实验数据简介为了验证所提出的ML-NSNRC多标签学习算法的性能,本文选取3个常用的多标签数据集:自然场景数据集[3]、Yeast基因数据集和scene数据集[14]进行多标签分类实验。
1) 自然场景数据集
在自然场景数据集下,多标签学习算法通过已标记的训练图像对测试图像的标签集进行预测。该数据集包含了2 000张自然场景的图像,其中每张图像的标签都已经过人工交互判断标定,标签包括沙漠、山、海洋、日落、树木。该数据集中超过22%的风景图像同时属于多个类别,其中每张图像的平均标签个数为1.24±0.44个,每张图像可表示为一个294维的特征向量。
2) Yeast基因数据集
多标签学习算法通过分析Yeast基因集中已知功能的Yeast基因,对待测试样本中的Yeast基因的功能进行标注。Yeast基因的功能类别被分为4层,本文实验采用的文献[5]中的方案,即仅仅使用顶层的功能类别。最终该数据集包含2417个基因,共有14个类别,每个基因由一个103维的特征向量表示,每个基因的平均标签个数为4.24$ \pm $1.57个。
3) scene数据集
scene数据集[14]的任务是通过已知标签集的训练图像来预测待分类样本图像的标签集。该数据集包含2 407张图像,其中每张图像包含落日、海滩、山川、原野、落叶、都市这6个标签中的一个或多个,每张图像可表示为一个294维的特征向量。
4.2 ML-NSNRC中参数初始化的影响本文所提出的ML-NSNRC迭代更新算法需要对稀疏系数进行初始化,不同初始稀疏系数会对迭代更新算法的收敛性产生影响。为了测试参数初始化带来的影响,分别采用全部平均1/n、绝对标准正态随机分布随机数$|N(0,1)|$、(0,1)均匀分布随机数、绝对最小二乘解以及最小二乘解正部对稀疏系数初始化。图 1显示了在自然场景数据集下,对所提出的ML-NSNRC算法采用5种不同的初始化方法,其目标函数值的迭代更新趋势可看出,不同的参数初始化对ML-NSNRC迭代更新算法并未造成较大的影响,而且所提出的优化方法收敛速度非常快。为了简化算法并节省时间,将稀疏系数s的每个元素初始值设为1/n。
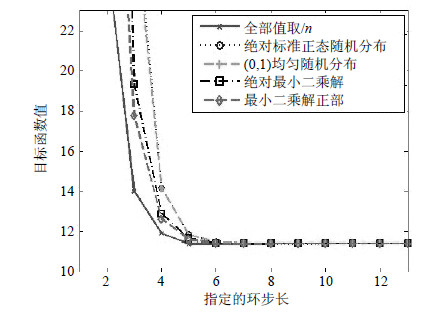 |
| 图1 不同稀疏系数初始化对ML-NSNRC收敛性的影响 |
用k-近邻来近似表示数据中非线性流形的局部结构时,近邻数k的选择至关重要。不同数据分布形状及不同的数据采集密度都需要设置不同的近邻数k。在ML-NSNRC中,近邻数k值受到库中每类标签正负样本个数的影响,如训练样本集中标签l的正样本数为n1,负样本数为n2,其中n1<<n2,那么k必须小于等于n1。为了测试不同近邻数k对所提出的ML-NSNRC的影响,分别取近邻数k为5的正整数倍,在scene数据集上进行多标签学习。图 2显示了ML-NSNRC和ML-KNN的平均分类精度随着不同近邻数k的变化情况。为了便于比较,将相同实验配置下的ML-SRC和ML-NSRC的平均分类精度用水平线表示。从图中可知当k取20时ML-NSNRC的平均精度达到较好水平,当k取5时ML-KNN的平均精度达到较好水平。
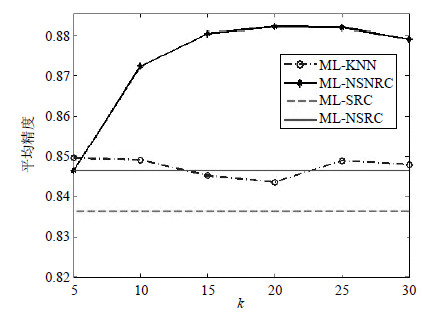 |
| 图2 近邻数k对ML-NSNRC和ML-KNN平均精度的影响 |
利用文献[3]中的多标签算法评价标准验证本文所提出的算法的有效性。评价标准包括汉明损失、1-错误率、排序损失、覆盖率、平均精度这5个方面,其中,平均精度的值越大表示多标签算法越好,而其他4个标准则是值越小表示算法越好。在实施ML-SRC时对稀疏系数限制为非负,提出非负稀疏表示的多标签学习算法(ML-NSRC)。为了进一步验证本文算法的性能,将所提出的ML-NSNRC与3种多标签学习算法进行比较。这3种算法分别是基于k-近邻和传统贝叶斯的多标签学习算法ML-KNN、基于稀疏表示的多标记学习算法ML-SRC和基于非负稀疏表示的多标签学习算法ML-NSRC。其中ML-KNN和ML-SRC均是当前多标签学习领域效果最好的方法之一。ML-NSNRC实验中非负稀疏系数求解的迭代次数为100次,自然场景数据集下k取400,Yeast数据集下k取5,scene数据集下k取20。
表 1是4种多标签学习算法在自然场景数据集上的性能比较。可看出,在自然场景数据集上,本文所提出的算法在1-错误率、覆盖率、排序损失和平均精度上比其他3种算法表现更佳。其中,汉明损失比ML-KNN低19.4%,覆盖率比ML-KNN低14.7%,平均精度比ML-KNN高4.3%。
| 表1 4种多标签学习算法在自然场景数据集上的性能比较 |
表 2是4种多标签学习算法在Yeast基因集上的性能比较,其中ML-SRC和ML-NSRC采用了十折交叉验证的方法。可知在Yeast基因集上,本文所提出的算法在汉明损失、覆盖率、排序损失和平均精度这4个性能指标上比其他3种算法更佳。其中,汉明损失比ML-KNN降低18.5%,排序损失比ML-KNN降低9%,平均精度比ML-KNN和ML-SRC提高1.6%。
| 表2 4种多标签学习算法在Yeast数据集上的性能比较 |
表 3是4种多标签学习算法在scene数据集上的性能比较。可知本文算法在各项指标上都优于其他3种算法。其中,本文算法的汉明损失比ML-KNN和ML-SRC分别降低18.2%和21.4%,覆盖率比ML- KNN降低32.6%,平均精度比ML-KNN和ML-SRC分别提高了4.3%和5.6%。
| 表3 4种多标签学习算法在scene数据集上的性能比较 |
通过比较自然场景图像数据集、Yeast基因数据集以及scene数据集上的实验结果可知,本文所提出的ML-NSNRC算法在分类精确度上比ML-KNN、ML-SRC、ML-NSRC算法均有明显提高,在其他4项指标上也表现出较好的水平。本文所提出的算法结合了非负稀疏表示的有效鉴别能力,和k-近邻方法对非线性流形数据集的局部线性整理,可以有效解决多标签数据分类问题。
5 结束语本文提出了一种非负稀疏近邻表示分类算法(NSNRC),将其成功地应用到多标签数据分类中,并提出一种非负稀疏近邻表示分类的多标签学习算法ML-NSNRC。将待测试样本在训练样本每一类中的k-近邻作为待测试样本的训练样本基,并在稀疏编码过程中对稀疏系数加入非负性限制。该算法有效克服了非线性流形数据对算法的影响,并且得到了全为非负值的稀疏系数,从而为数据的标签分类保留了更多的判别信息。提出一种快速优化迭代求解算法,并给出其收敛到全局最优的证明。在自然场景图像、Yeast基因、scene这3个数据集上的实验结果表明,所提出的算法在性能上优于其他经典算法,符合预期目标。下一阶段需要寻求更优的稀疏模型,进一步提高多标签分类效果。
| [1] | Schapire R E, Singer Y. Boostexter: a boosting-based system for text categorization[J]. Machine Learning, 2000, 39(2-3): 135-168. |
| [2] | Ueda N, Saito K. Parametric mixture models for multi-label text[J]. Advances in Neural Information Processing, 2003(15): 721-728. |
| [3] | Zhang M L, Zhou Z H. ML-KNN: a lazy learning approach to multi-label learning[J]. Pattern Recognition, 2007, 40(7): 2038-2048. |
| [4] | Sanden C, Zhang J Z. Enhancing multi-label music genre classification through ensemble techniques[C] //Proceedings of the 34th international ACM SIGIR Conference on Research and development in Information Retrieval. New York: ACM, 2011: 705-714. |
| [5] | Elisseeff A, Weston J. A kernel method for multi-labelled classification[J]. Advances in Neural Information Processing, 2002(14): 681-687. |
| [6] | Candès E J, Romberg J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. |
| [7] | Wright J, Yang A Y, GANESH A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. |
| [8] | JI Y, LIN T, ZHA H. Mahalanobis distance based non-negative sparse representation for face recognition[C]// International Conference on Machine Learning and Applications. Miami, FL: IEEE, 2009: 41-46. |
| [9] | Hui K, Li C, Zhang L. Sparse neighbor representation for classification[J]. Pattern Recognition Letters, 2012, 33(5): 661-669. |
| [10] | 宋相法, 焦李成. 基于稀疏表示的多标记学习算法[J]. 模式识别与人工智能, 2012, 25(1): 124-129. SONG Xiang-fa, JIAO Li-cheng. A multi-label learning algorithm based on sparse representation[J]. Pattern Recognition and Artificial Intelligence, 2012, 25(1): 124-129. |
| [11] | Tibshirani R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society (Series B, Methodological), 1996, 58(1): 67-88. |
| [12] | Lee D D, Seung H S. Algorithms for non-negative matrix factorization[J]. Advances in Neural Information Processing, 2001(2): 556-562. |
| [13] | Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. |
| [14] | Boutell M R, Luo J, Shen X, et al. Learning multi-label scene classification[J]. Pattern Recognition, 2004, 37(9): 1757-1771. |
 2015, Vol. 44
2015, Vol. 44
