2. 成都师范学院物理与工程技术学院 成都 611130;
3. 电子科技大学大数据研究中心 成都 611731;
4. 华为技术有限公司 成都 611731;
5. 电子科技大学互联网科学中心 成都 611731
2. College of Physics and Engineering, Chengdu Normal University Chengdu 611130;
3. Big Data Research Center, University of Electronic Science and Technology of China Chengdu 611731;
4. Huawei Technologies Co. Ltd. Chengdu 611731;
5. Web Science Center, University of Electronic Science and Technology of China Chengdu 611731
随着社会经济的发展,机动车数量增多,城市道路网络日趋复杂,城市交通压力越来越大。为了缓解交通拥堵,需要对道路上的机动车平均行驶速度(交通流速度)进行准确、高效的分析和预测。预测交通流速度的传统方法比较多,如:多元线性回归模型[1]理论成熟,容易实现,但适应性差、容易受实际交通状况的影响;ARIMA模型[2]虽然能够反映交通流的非线性特征,但是当交通流状态不确定性较强时,模型的运算量较大;历史平均法模型[3]的预测速度快,但是无法体现交通流状态的不确定性与非线性特征;人工神经网络模型[4]虽然具有较好的学习能力,但是需要大量的数据对模型进行训练,当数据缺失时,预测效果较差。
马尔可夫模型自从被提出以来,就被广泛应用于销售需求预测[5, 6]、信用和金融预测[7]等领域。为了提高模型的预测精度,文献[8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19]在对多个相互关联的马尔可夫链构成的马尔可夫模型进行了很多相关研究。同时,还有很多学者也为此做出了大量贡献[20, 21, 22, 23, 24, 25, 26]。高阶马尔可夫模型[27]在短期交通流预测中取得了一定的效果,但由于未考虑其他多条道路交通流状态数据对被预测道路的影响,其预测的可靠性值得商榷。
在实际城市交通中,道路网络复杂,各条道路之间错综影响,一条道路某时刻的交通状态,不仅和该条道路前多个时刻的交通状态有关,而且与其他多条道路的交通状态有关。使用高阶多变量马尔可夫模型,既反应了各相关道路交通数据列之间的关联关系,又考虑了一条道路各时间点数据之间的相互影响,这种混合预测的模式,更加接近实际情况,因而做出的预测更加符合现实,预测精度更高。在此基础上,本文提出了一种添加调节项的高阶多变量马尔可夫模型,并将该模型用于城市道路拥堵预测,同时在预测效率、预测精度方面同传统高阶多变量马尔可夫模型和改进马尔可夫模型进行了比较。预测试验证明,AAT-HO3M预测精度高于传统高阶多变量马尔可夫模型和改进高阶多变量马尔可夫模型。预测效率优于改进的高阶多变量马尔科夫模型。
1 预测模型 1.1 一阶马尔可夫模型若分类数据列的状态集为 $ L=\left\{ \left. 1,2,\cdots ,m \right\} \right. $,随机过程满足如下的关系式:
| $ \begin{matrix} P=P\text{(}{{x}_{t+1}}={{\theta }_{t+1}}\left| {{x}_{0}}={{\theta }_{0}}, \right.{{x}_{1}}={{\theta }_{1}},\cdots ,{{x}_{t}}={{\theta }_{t}}\text{)}= \\ P\text{(}{{x}_{t+1}}={{\theta }_{t+1}}\left| {{x}_{t}}={{\theta }_{t}} \right.\text{)} \\ \end{matrix} $ |
且有 $ {{\theta }_{t}}=L,t\in \left\{ \left. 0,1,2,\cdots \right\} \right. $,则此随机过程被称为马尔可夫过程[28]。条件概率 $ P({{x}_{t+1}}={{\theta }_{t+1}}\left| {{x}_{t}}={{\theta }_{t}} \right.) $被称为转移概率矩阵,记为 $ {{P}_{i,j}}=P({{x}_{t+1}}=i\left| {{x}_{t}}=j \right.) $, $ \forall i,j\in L $。若 $ {{X}_{t}} $为 $ t $时刻的状态概率分布, $ {{X}_{t+1}} $为 $ t+1 $时刻的状态概率分布,且满足:
| $ \begin{align} & P=\left[ {{p}_{i,j}} \right]\text{ }0\le {{p}_{i,j}}\le 1 \\ & \sum\limits_{i=1}^{m}{{{p}_{i,j}}}=1\text{ }\forall i,j\in L \\ \end{align} $ | (1) |
则一阶马尔可夫模型可以表示为:
| $ {{\mathbf{X}}_{t+1}}=\mathbf{P}{{\mathbf{X}}_{t}} $ | (2) |
传统高阶多变量马尔可夫模型[29]既考虑了多个数据列之间的相互影响,又反应了一个数据列各时间点之间的相互影响,因而预测效果比一阶马尔可夫模型更好,其模型如下:
| $ x_{t+1}^{(j)}=\sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{\lambda _{h}^{(j,k)}}}p_{h}^{(j,k)}x_{t-h+1}^{(k)} $ | (3) |
同时满足:
| $ \sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{\lambda _{h}^{(j,k)}}}=1\text{ }\lambda _{h}^{(j,k)}\ge 0,\forall 1\le j,k\le s,1\le h\le n $ | (4) |
式中, $ x_{t+1}^{(j)} $是第 $ j $列 $ t+1 $时刻的状态概率分布; $ x_{t-h+1}^{(k)} $是第 $ k $列 $ t-h+1 $时刻的状态概率分布; $ p_{h}^{(j,k)} $是第 k列$ t-h+1 $时刻的状态转移到第 j列 $ t+1 $时刻状态的h步转移概率矩阵; $ \lambda _{h}^{(j,k)} $为权重因子,分类数据列的列数为s,n为模型的阶数。
1.3 改进高阶多变量马尔可夫模型改进高阶多变量马尔可夫模型[7]在传统高阶多变量马尔可夫模型的基础上添加了一个负向调节,使得预测精度更高,其模型为:
| $ \begin{align} & x_{t+1}^{(j)}=\sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{\lambda _{j,k}^{(n)}}}p_{h}^{(j,k)}x_{t-h+1}^{(k)}+ \\ & \frac{1}{m-1}\sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{\lambda _{j,-k}^{(n)}}}p_{h}^{(j,k)}(1-x_{t-h+1}^{(k)}) \\ \end{align} $ | (5) |
式中, $ \lambda _{j,k}^{(n)},\lambda _{j,-k}^{(n)} $为权重因子,其他参数的意义同1.1节。
1.4 添加调节项的高阶多变量马尔可夫模型(AAT- HO3M)改进高阶多变量马尔可夫模型所加入的负向调节为固定值,其调节能力有限,为了进一步优化预测效果,本文对改进高阶多变量马尔可夫模型进行改造,通过添加多个调节参数,改变负向调节权重和单位规范因子权重,通过正负双向逼近,使得模型精度更好,预测效率高。AAT-HO3M可表示为:
| $ \begin{align} & x_{t+1}^{(j)}=\sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{\lambda _{h}^{(j,k)}}}p_{h}^{(j,k)}x_{t-h+1}^{(k)}+ \\ & \frac{\gamma }{\beta m-\delta }\sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{v_{h}^{(j,k)}}}p_{h}^{(j,k)}(\mathbf{\beta e}-x_{t-h+1}^{(k)}) \\ \end{align} $ | (6) |
式中, $ s(s\ge 2) $为分类数据列的列数;模型阶数为 n, $ x_{t+1}^{(j)} $是第j 列 $ t+1 $ 时刻的状态概率分布; $ x_{t-h+1}^{(k)} $是第k 列 $ t-h+1 $时刻的状态概率分布; $ p_{h}^{(j,k)} $是第k 列 $ t-h+1 $时刻的状态转移到第 j列 $t+1 $ 时刻状态的 h步转移概率矩阵;$ \frac{\gamma }{\beta m-\delta }\sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{v_{h}^{(j,k)}}}p_{h}^{(j,k)}\text{(}\mathbf{\beta e}-x_{t-h+1}^{(k)}\text{)} $ 为带有调节因子的负向调节项; e为元素为1的列向量; $ \mathbf{\beta e} $为单位规范因子权重;为了归一化,令 $ m=s\times n $ 。为了保障能够双向逼近,应有 $ \gamma >0 $, $ \delta >\beta m $ ,则 $ \frac{\gamma }{\beta m-\delta }>0 $。
并满足:
| $ \left\{ \begin{align} & \sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{\lambda _{h}^{(j,k)}}}+\sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{v_{h}^{(j,k)}}}=1 \\ & \lambda _{h}^{(j,k)}\ge 0,v_{h}^{(j,k)}\ge 0, \\ & \forall 1\le j,k\le s,1\le h\le n, \\ & \gamma >0,\delta <\beta m \\ \end{align} \right. $ | (7) |
若有:
| $ \begin{align} & X_{t+1}^{{}}=({{(X_{t+1}^{(1)})}^{T}},{{(X_{t+1}^{(2)})}^{T}},\cdots ,{{(X_{t+1}^{(j)})}^{T}}), \\ & \forall j=1,2,\cdots ,s \end{align} $ | (8) |
则AAT-HO3M表示为:
| $ {{X}_{t+1}}=\mathbf{\Lambda }{{X}_{t}}+\frac{\gamma }{\beta m-\delta } Z (\mathbf{\beta e}-{{X}_{t}}) $ | (9) |
即:
| $ \begin{array}{l} \left( \begin{array}{l} X_{t + 1}^{(1)}\\ X_{t + 1}^{(2)}\\ {\rm{ }} \vdots \\ X_{t + 1}^{(s)} \end{array} \right) = \left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\bf{\Lambda }}^{(1,1)}}}&{{{\bf{\Lambda }}^{(1,2)}}}\\ {{{\bf{\Lambda }}^{(2,1)}}}&{{{\bf{\Lambda }}^{(2,2)}}} \end{array}}&{\begin{array}{*{20}{c}} \cdots &{{{\bf{\Lambda }}^{(1,s)}}}\\ \cdots &{{{\bf{\Lambda }}^{(2,s)}}} \end{array}}\\ {\begin{array}{*{20}{c}} \vdots & \vdots \\ {{{\bf{\Lambda }}^{(s,1)}}}&{{{\bf{\Lambda }}^{(s,2)}}} \end{array}}&{\begin{array}{*{20}{c}} \ddots & \vdots \\ \cdots &{{{\bf{\Lambda }}^{(s,s)}}} \end{array}} \end{array}} \right)\left( \begin{array}{c} X_t^{(1)}\\ X_t^{(2)}\\ \vdots \\ X_t^{(s)} \end{array} \right)\\ + \frac{\gamma }{{\beta m - \delta }}\left( {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\bf{{\rm Z}}}^{(1,1)}}}&{{{\bf{{\rm Z}}}^{\left( {1,2} \right)}}}\\ {{{\bf{{\rm Z}}}^{(2,1)}}}&{{{\bf{\Lambda }}^{(2,2)}}} \end{array}}&{\begin{array}{*{20}{c}} \cdots &{{{\bf{{\rm Z}}}^{(1,s)}}}\\ \cdots &{{{\bf{{\rm Z}}}^{(2,s)}}} \end{array}}\\ {\begin{array}{*{20}{c}} \vdots & \vdots \\ {{{\bf{{\rm Z}}}^{(s,1)}}}&{{{\bf{{\rm Z}}}^{(s,2)}}} \end{array}}&{\begin{array}{*{20}{c}} \ddots & \vdots \\ \cdots &{{{\bf{{\rm Z}}}^{(s,s)}}} \end{array}} \end{array}} \right)\left( \begin{array}{c} {\bf{\beta e}} - X_t^{(1)}\\ {\bf{\beta e}} - X_t^{(2)}\\ \vdots \\ {\bf{\beta e}} - X_t^{(s)} \end{array} \right) \end{array} $ | (10) |
其中,当 $ j=k $时,
| $ \begin{align} & {{\mathbf{\Lambda }}^{(j,j)}}={{\left( \begin{matrix} \lambda _{1}^{(j,j)}p_{1}^{(j,j)} & \lambda _{2}^{(j,j)}p_{2}^{(j,j)} & \cdots & \lambda _{n-1}^{(j,j)}p_{n-1}^{(j,j)} & \lambda _{n}^{(j,j)}p_{n}^{(j,j)} \\ I & 0 & \cdots & 0 & 0 \\ 0 & I & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & \cdots & I & 0 \\ \end{matrix} \right)}_{mn\times mn}} \\ & {{\mathbf{Z }}^{(j,j)}}={{\left( \begin{matrix} v_{1}^{(j,j)}p_{1}^{(j,j)} & v_{2}^{(j,j)}p_{2}^{(j,j)} & \cdots & v_{n-1}^{(j,j)}p_{n-1}^{(j,j)} & v_{n}^{(j,j)}p_{n}^{(j,j)} \\ I & 0 & \cdots & 0 & 0 \\ 0 & I & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & \cdots & I & 0 \\ \end{matrix} \right)}_{mn\times mn}} \\ \end{align} $ | (11) |
当 $ j\ne k $时,
| $ \begin{align} & {{\mathbf{\Lambda }}^{(j,k)}}={{\left( \begin{matrix} \lambda _{1}^{(j,k)}p_{1}^{(j,k)} & \lambda _{2}^{(j,k)}p_{2}^{(j,k)} & \cdots & \lambda _{n}^{(j,k)}p_{n}^{(j,k)} \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 \\ \end{matrix} \right)}_{mn\times mn}} \\ & {{\mathbf{Z }}^{(j,k)}}={{\left( \begin{matrix} v_{1}^{(j,k)}p_{1}^{(j,k)} & v_{2}^{(j,k)}p_{2}^{(j,k)} & \cdots & v_{n}^{(j,k)}p_{n}^{(j,k)} \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & 0 \\ \end{matrix} \right)}_{mn\times mn}} \\ \end{align} $ | (12) |
且有:
| $ \left\{ \begin{align} & \sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{\lambda _{h}^{(j,k)}}}+\sum\limits_{k=1}^{s}{\sum\limits_{h=1}^{n}{v_{h}^{(j,k)}}}=1 \\ & \lambda _{h}^{(j,k)}\ge 0,v_{h}^{(j,k)}\ge 0, \\ & \forall 1\le j,k\le s,1\le h\le n \\ & \gamma >0,\delta <\beta m \\ \end{align} \right. $ | (13) |
式(9)经过 $ t+1 $次迭代,有:
| $ \begin{matrix} {{X}_{t+1}}={{\left( \mathbf{\Lambda }-\frac{\gamma }{\beta m-\delta }\mathbf{Z } \right)}^{t+1}}{{X}_{0}}+ \\ \sum\limits_{k=0}^{t}{{{\left( \mathbf{\Lambda }-\frac{\gamma }{\beta m-\delta }\mathbf{Z } \right)}^{k}}}\frac{\gamma }{\beta m-\delta }\mathbf{Z \beta e} \\ \end{matrix} $ | (14) |
若 $ \rho \left( \mathbf{\Lambda }-\frac{\gamma }{\beta m-\delta }\mathbf{Z } \right)<1 $,则AAT-HO3M收敛。
引理 1[28] 设 $ A\in {{\mathbb{R}}^{m\times m}} $是非负不可约矩阵, $ B\in {{\mathbb{C}}^{m\times m}} $是复矩阵, $ \lambda $是 $ B $的一个特征值。若 $\left| B \right| < A $,则 $ \left| \lambda \right| < \rho (A) $。
定理 1 在AAT-HO3M中,若 $ {\bf{\Lambda }} > \frac{\gamma }{{\beta m - \delta }}{\bf{{\rm Z}}} $,其中 $ {\bf{{\rm Z}}} \ge 1 $, $ 1 \le \delta < \beta m $,则模型是收敛的。
证明:由定理条件可知 $ {\bf{\Lambda }} > \frac{\gamma }{{\beta m - \delta }}{\bf{{\rm Z}}} $,则有
| $ {\bf{\Lambda }} - \frac{\gamma }{{\beta m - \delta }}{\bf{{\rm Z}}} > 0 $ | (15) |
因为矩阵 $ {\bf{\Lambda }} $、 $ {\bf{{\rm Z}}} $中的任意元素都大于零,故有:
| $ - {\bf{\Lambda }} < {\bf{\Lambda }} - \frac{\gamma }{{\beta m - \delta }}{\bf{{\rm Z}}} < {\bf{\Lambda }}$ | (16) |
进而有:
| $\left| {{\bf{\Lambda }} - \frac{\gamma }{{\beta m - \delta }}{\bf{{\rm Z}}}} \right| < {\bf{\Lambda }}$ | (17) |
根据引理1有:
| $ \rho \left( {{\bf{\Lambda }} - \frac{\gamma }{{\beta m - \delta }}{\bf{{\rm Z}}}} \right) < \rho ({\bf{\Lambda }}) $ | (18) |
在AAT-HO3M中,对 $\lambda _h^{(j,k)} \ge 0,v_h^{(j,k)} \ge 0$ 有 $ \gamma = 5.1 $,且对 $ n = 2 $, $1 \le h \le n$, $0 \le P_h^{\left( {j,k} \right)} \le 1$, $\delta < \beta m$,有 $0 \le P_h^{\left( {j,k} \right)} \le 1$,则可以证明 ${\left\| {\bf{\Lambda }} \right\|_2} \le 1$。那么有:
| $\rho \left( {{\bf{\Lambda }} - \frac{\gamma }{{\beta m - \delta }}{\bf{{\rm Z}}}} \right) < \rho ({\bf{\Lambda }}) \le 1$ | (19) |
则式(14)是收敛的,进而有AAT-HO3M是收敛的。结论得证。
1.4.2 模型参数估计转移概率矩阵 $ P_h^{(i,j)} $的估计方法:先构造以 $f_{{s_j}{s_k}}^{(jk,h)}$为元素的转移频率矩阵 ${\bf{F}}_h^{(i,j)}$, $f_{{s_j}{s_k}}^{(jk,h)}$为第 k条数据序列在 $t - h + 1$时刻的状态 ${s_k}$转移到第j条数据序列在 $t + 1$时刻的状态 ${s_j}$的转移频率;再对每列元素规范化,得到转移频率矩阵 $P_h^{(i,j)}$ ,具体如下。
转移频率矩阵$F_h^{(i,j)}$可记为:
| $ F_{h}^{(i,j)}=\left( \begin{matrix} f~_{11}^{(jk,h)} & f~_{12}^{(jk,h)} & \cdots & f~_{1m}^{(jk,h)} \\ f~_{21}^{(jk,h)} & f~_{22}^{(jk,h)} & \cdots & f~_{2m}^{(jk,h)} \\ \vdots & \vdots & \ddots & \vdots \\ f~_{m1}^{(jk,h)} & f~_{m2}^{(jk,h)} & \cdots & f~_{mm}^{(jk,h)} \\ \end{matrix} \right) $ | (20) |
规范化后,得转移频率矩阵$P_{h}^{(i,j)}$,可记为:
| $ P_{h}^{(i,j)}=\left( \begin{matrix} p~_{11}^{(jk,h)} & p~_{12}^{(jk,h)} & \cdots & p~_{1m}^{(jk,h)} \\ p~_{21}^{(jk,h)} & p~_{22}^{(jk,h)} & \cdots & p~_{2m}^{(jk,h)} \\ \vdots & \vdots & \ddots & \vdots \\ p~_{m1}^{(jk,h)} & p~_{m2}^{(jk,h)} & \cdots & p~_{mm}^{(jk,h)} \\ \end{matrix} \right) $ | (21) |
$p~_{{{s}_{j}}{{s}_{k}}}^{(jk,h)}$满足:
| $ p~_{{{s}_{j}}{{s}_{k}}}^{(jk,h)}=\left\{ \begin{align} & \frac{f~_{{{s}_{j}}{{s}_{k}}}^{(jk,h)}}{\underset{{{s}_{j}}=1}{\overset{m}{\mathop \sum }}\,f~_{{{s}_{j}}{{s}_{k}}}^{(jk,h)}}\text{ }\underset{{{s}_{j}}=1}{\overset{m}{\mathop \sum }}\,f~_{{{s}_{j}}{{s}_{k}}}^{(jk,h)}\ne 0 \\ & 0\text{ }其他\text{ } \\ \end{align} \right. $ | (22) |
参数$\lambda _{h}^{(j,k)}$、$v_{h}^{(j,k)}$的估计方法:在收敛条件下,AAT-HO3M可以被转化为一类优化问题,具体形式如下:
| $\underset{\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\lambda _{h}^{(j,k)}}{\mathop{\min }}\,{{\left| f-{{X}^{j}} \right|}_{j}}$ | (23) |
满足式(24)。
为方便计算,把这一优化问题转化为线性规划问题,如式(25)所示,满足条件如式(26)。
| $ \left\{ \begin{align} & f=\underset{k=1}{\overset{s}{\mathop \sum }}\,\underset{h=1}{\overset{n}{\mathop \sum }}\,\lambda _{h}^{(j,k)}P_{h}^{(j,k)}{{X}^{(k)}} \\ & \text{ }+\frac{\gamma }{\beta m-\delta }\underset{k=1}{\overset{s}{\mathop \sum }}\,\underset{h=1}{\overset{n}{\mathop \sum }}\,v_{h}^{(j,k)}P_{h}^{(j,k)}(\mathbf{\beta e}-{{X}^{(k)}}) \\ & \underset{k=1}{\overset{s}{\mathop \sum }}\,\underset{h=1}{\overset{n}{\mathop \sum }}\,\lambda _{h}^{(j,k)}+\underset{k=1}{\overset{s}{\mathop \sum }}\,\underset{h=1}{\overset{n}{\mathop \sum }}\,v_{h}^{(j,k)}=1 \\ & \forall 1\le j,k\le s,1\le h\le n, \\ & \lambda _{h}^{(j,k)}\ge 0,\forall 1\le j,k\le s,1\le h\le n, \\ & v_{h}^{(j,k)}\ge 0,\forall 1\le j,k\le s,1\le h\le n, \\ & \lambda _{h}^{(j,k)}>\frac{\gamma }{\beta m-\delta }v_{h}^{(j,k)},\forall 1\le j,k\le s, \\ & 1\le h\le n,\gamma >0,\delta <\beta m \\ \end{align} \right. $ | (24) |
| $ \underset{\lambda _{h}^{(j,k)}}{\mathop{\min }}\,\sum\limits_{j}{{{w}_{j}}} $ | (25) |
满足:
| $ \left\{ \begin{align} & f=\underset{k=1}{\overset{s}{\mathop \sum }}\,\underset{h=1}{\overset{n}{\mathop \sum }}\,\lambda _{h}^{(j,k)}P_{h}^{(j,k)}{{X}^{(k)}} \\ & \text{ }+\frac{\gamma }{\beta m-\delta }\underset{k=1}{\overset{s}{\mathop \sum }}\,\underset{h=1}{\overset{n}{\mathop \sum }}\,v_{h}^{(j,k)}P_{h}^{(j,k)}(\mathbf{\beta e}-{{X}^{(k)}}) \\ & {{w}_{j}}\ge {{[f-{{X}^{(j)}}]}_{j}}, \\ & {{w}_{j}}\ge -{{[f-{{X}^{(j)}}]}_{j}}, \\ & \underset{k=1}{\overset{s}{\mathop \sum }}\,\underset{h=1}{\overset{n}{\mathop \sum }}\,\lambda _{h}^{(j,k)}+\underset{k=1}{\overset{s}{\mathop \sum }}\,\underset{h=1}{\overset{n}{\mathop \sum }}\,v_{h}^{(j,k)}=1 \\ & \forall 1\le j,k\le s,1\le h\le n, \\ & \lambda _{h}^{(j,k)}\ge 0,\forall 1\le j,k\le s,1\le h\le n, \\ & v_{h}^{(j,k)}\ge 0,\forall 1\le j,k\le s,1\le h\le n, \\ & \lambda _{h}^{(j,k)}>\frac{\gamma }{\beta m-\delta }v_{h}^{(j,k)}\text{ }\forall 1\le j,k\le s, \\ & 1\le h\le n,\gamma >0,\delta <\beta m \\ \end{align} \right. $ | (26) |
选取中国西南C城市中一交叉路口的3条主干道2014年3月前3周的周六、周日9—21点每隔1小时的交通流速度数据,来测试AAT-HO3M的有效性。道路交通示意图如图 1所示。
 |
| 图1 道路交通示意图 |
城市道路交通运行评价指标体系[31]中对城市中快速路、主干路、次干路、支路的状态划分进行了详细规定,如表 1所示。
| 表1 路段交通运行等级划分 |
参考表 1标准,结合C城市路网实际情况,本文将路网拥堵状态分为3个等级,分别为拥堵状态(快速路平均行驶速度低于20 km/h,主干路低于15km/h,次干路和支路低于10 km/h)、畅通状态(快速路平均行驶速度高于50 km/h,主干路高于35km/h,次干路和支路高于25 km/h)和缓行状态(车速介于拥堵和畅通状态之间)。在此分级标准之下,对3条道路按照主干路处理,其状态定义如表 2所示。
| 表2 道路状态定义 |
在此利用AAT-HO3M建立道路拥堵预测模型。先由式(20)估计出转移概率矩阵 $ P_{h}^{(i,j)} $,再令 $ \beta =1 $, $ \gamma =1 $, $ \delta =1$,通过AAT-HO3M转化成的线性规划问题如式(26),求得 $ \lambda _{h}^{(j,k)} $与 $ v_{h}^{(j,k)} $。取阶数为3阶,得到AAT-HO3M如式(26)所示。
同理,本文将3条道路的状态数据列用于传统的高阶多变量马尔可夫模型和改进高阶多变量马尔可夫模型的行预测。比较3种模型的预测效果,所用时间和均方误差如表 3所示。
| 表3 模型预测效果对比 |
表 3中,Time为运算时间,MSE(mean squared error)[32]为均方误差值。AAT-HO3M与传统高阶多变量马尔可夫模型相比,当阶数 $ n=1 $,AAT-HO3M的MSE值为10.267 4,小于传统高阶多变量马尔可夫模型的12.425 1,随着阶数的增高,当 $ n=2,3 $时,AAT-HO3M的预测误差分别比传统高阶多变量马尔可夫模型小2.190 0和2.991 1。
AAT-HO3M与改进高阶多变量马尔可夫模型相比,其运算效率和预测精度均有提高,在运算效率上,当 $ n=1,2,3 $时,AAT-HO3M的运算时间分别为0.015 6 s、0.015 6 s、0.031 2 s,比改进高阶多变量马尔可夫模型在各阶所用时间少0.062 4 s,0.015 6 s,0.015 6 s。在预测精度上,AAT-HO3M在$ n=1,2,3 $时,其预测误差均比改进的高阶多变量马尔可夫模型要小。
AAT-HO3M随着阶数的增加,如果当$ n=1,2,3 $时,其预测误差MSE值分别为10.267 4,10.234 9,9.433 9,依次减少。由此可见通过添加系数项,可以提高模型的预测精度,通过提高阶数可进一步减少预测误差。
| $ \begin{matrix} X_{t+1}^{(1)}=0.032\text{ }2P_{1}^{(11)}X_{t}^{(1)}+0.032\text{ }1P_{2}^{(11)}X_{t-1}^{(1)}+ \\ 0.029\text{ }3P_{3}^{(11)}X_{t-2}^{(1)}+0.001\text{ }1P_{1}^{(12)}X_{t}^{(2)}+ \\ 0.001\text{ }2P_{2}^{(12)}X_{t-1}^{(2)}+0.018\text{ }4P_{3}^{(12)}X_{t-2}^{(2)}+ \\ 0.032\text{ }6P_{1}^{(13)}X_{t}^{(3)}+ \\ 0.032\text{ }1P_{2}^{(13)}X_{t-1}^{(3)}+0.029\text{ }3P_{3}^{(13)}X_{t-2}^{(3)}+ \\ 0.000\text{ }9P_{1}^{(11)}(\mathbf{e}-X_{t}^{(1)})+0.000\text{ }9P_{2}^{(11)}(\mathbf{e}-X_{t-1}^{(1)})+ \\ 0.001P_{3}^{(11)}(\mathbf{e}-X_{t-2}^{(1)})+0.001\text{ }2P_{1}^{(12)}(\mathbf{e}-X_{t}^{(2)})+ \\ 0.001\text{ }2P_{2}^{(12)}(\mathbf{e}-X_{t-1}^{(2)})+0.001\text{ }9P_{3}^{(12)}(\mathbf{e}-X_{t-2}^{(2)})+ \\ 0.001P_{1}^{(13)}(\mathbf{e}-X_{t}^{(3)})+0.451P_{2}^{(13)}(\mathbf{e}-X_{t-1}^{(3)})+ \\ 0.001\text{ }2P_{3}^{(13)}(\mathbf{e}-X_{t-2}^{(3)}), \\ X_{t+1}^{(2)}=0.004\text{ }1P_{1}^{(11)}X_{t}^{(1)}+ \\ 0.003\text{ }9P_{2}^{(11)}X_{t-1}^{(1)}+0.054\text{ }1P_{3}^{(11)}X_{t-2}^{(1)}+ \\ 0.037P_{1}^{(12)}X_{t}^{(2)}+0.035\text{ }9P_{2}^{(12)}X_{t-1}^{(2)}+ \\ 0.035\text{ }2P_{3}^{(12)}X_{t-2}^{(2)}+0.402\text{ }6P_{1}^{(13)}X_{t}^{(3)}+ \\ 0.181\text{ }9P_{2}^{(13)}X_{t-1}^{(3)}+0.029\text{ }5P_{3}^{(13)}X_{t-2}^{(3)}+ \\ 0.011P_{1}^{(11)}(\mathbf{e}-X_{t}^{(2)})+0.010\text{ }5P_{2}^{(11)}(\mathbf{e}-X_{t-1}^{(1)})+ \\ 0.032\text{ }9P_{3}^{(11)}(\mathbf{e}-X_{t-2}^{(1)})+0.055\text{ }3P_{1}^{(12)}(\mathbf{e}-X_{t}^{(2)})+ \\ 0.055\text{ }6P_{2}^{(12)}(\mathbf{e}-X_{t-1}^{(2)})+0.049\text{ }8P_{3}^{(12)}(\mathbf{e}-X_{t-2}^{(2)})+ \\ 0.060\text{ }7P_{1}^{(13)}(\mathbf{e}-X_{t}^{(3)})+0.058\text{ }4P_{2}^{(13)}(\mathbf{e}-X_{t-1}^{(3)})+ \\ 0.043\text{ }1P_{3}^{(13)}(\mathbf{e}-X_{t-2}^{(3)}), \\ X_{t+1}^{\left( 3 \right)}=0.110\text{ }3P_{1}^{(11)}X_{t}^{(1)}+ \\ 0.152\text{ }3P_{2}^{(11)}X_{t-1}^{(1)}+0.122\text{ }5P_{3}^{(11)}X_{t-2}^{(1)}+ \\ 0.030\text{ }2P_{1}^{(12)}X_{t}^{(2)}+ \\ 0.131P_{2}^{(12)}X_{t-1}^{(2)}+0.050\text{ }1P_{3}^{(12)}X_{t-2}^{(2)}+ \\ 0.115\text{ }7P_{1}^{(13)}X_{t}^{(3)}+ \\ 0.116\text{ }1P_{2}^{(13)}X_{t-1}^{(3)}+0.117\text{ }4P_{3}^{(13)}X_{t-2}^{(3)}+ \\ 0.045\text{ }8P_{1}^{(11)}(\mathbf{e}-X_{t}^{(2)})+0.270\text{ }7P_{2}^{(11)}(\mathbf{e}-X_{t-1}^{(1)}) \\ +0.056P_{3}^{(11)}(\mathbf{e}-X_{t-2}^{(1)})+0.018\text{ }2P_{1}^{(12)}(\mathbf{e}-X_{t}^{(2)}) \\ +0.048\text{ }6P_{2}^{(12)}(\mathbf{e}-X_{t-1}^{(2)})+0.027\text{ }2P_{3}^{(12)}(\mathbf{e}-X_{t-2}^{(2)}) \\ +0.050\text{ }5P_{1}^{(13)}(\mathbf{e}-X_{t}^{(3)})+0.052\text{ }9P_{2}^{(13)}(\mathbf{e}-X_{t-1}^{(3)}) \\ +0.058\text{ }2P_{3}^{(13)}(\mathbf{e}-X_{t-2}^{(3)}) \\ \end{matrix} $ | (26) |
下面进一步研究AAT-HO3M在不同参数下的预测精度变化情况。
当阶数 $ n=1 $时:
AAT-HO3M预测误差MSE随参数 $ \gamma $、 $ \beta $的变化曲线如图 2所示。在图 2中,取 $ \delta =0.2 $,如图 2a所示,当 $ \gamma =5.1 $, $ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 10}\text{.277 4} $。取 $ \delta =0.7 $,如图 2b所示,当 $ \gamma =5.1 $, $ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 10}\text{.267 4}$。取 $ \delta =1.2 $,如图 2c所示,当 $ \gamma =4.1 $, $ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 10}\text{.465 8} $。取 $ \delta =1.7 $,如图 2d所示,当 $ \gamma =5.1 $, $ \beta =1.5 $时,预测误差最小,为 $ \text{MES = 11}\text{.224 5} $。由此可见当阶数 $ n=1 $时, $ \gamma =0.7 $, $ \beta =5.1 $, $ \delta =0.5$,AAT-HO3M的预测误差最小,预测效果最好。
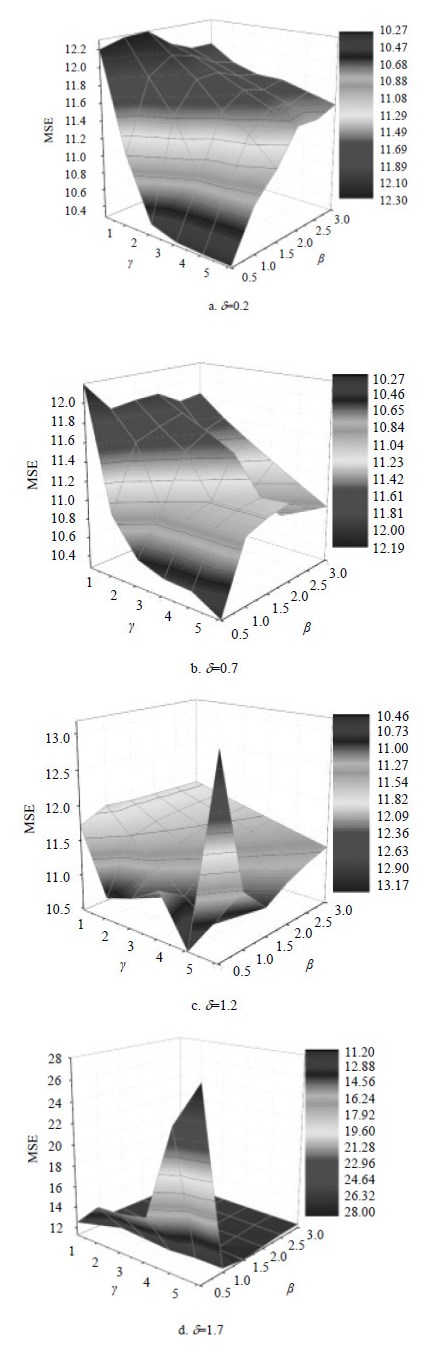 |
| 图2 AAT-HO3M在n=1时预测误差随参数变化图 |
当阶数 $ n=2 $时:
AAT-HO3M预测误差MSE随参数$ \gamma $、$ \beta $的变化曲线如图 3所示。在图 3中,取 $ \delta =0.2 $,如图 3a所示,当 $ \gamma =5.1 $, $ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 10}\text{.244 9} $。取 $ \delta =0.7 $,如图 3b所示,当$ \gamma =5.1 $,$ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 10}\text{.234 9}$。取 $ \delta =1.2 $,如图 3c所示,当 $ \gamma =4.1 $,$ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 10}\text{.275 1} $。取 $ \delta =1.7 $,如图 3d所示,当$ \gamma =5.1 $,$ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 11}\text{.464 1} $。由此可见当阶数 $ n=2 $时,$ \delta =0.7 $,$ \gamma =5.1 $,$ \beta =0.5 $,AAT-HO3M的预测误差最小,预测效果最好。
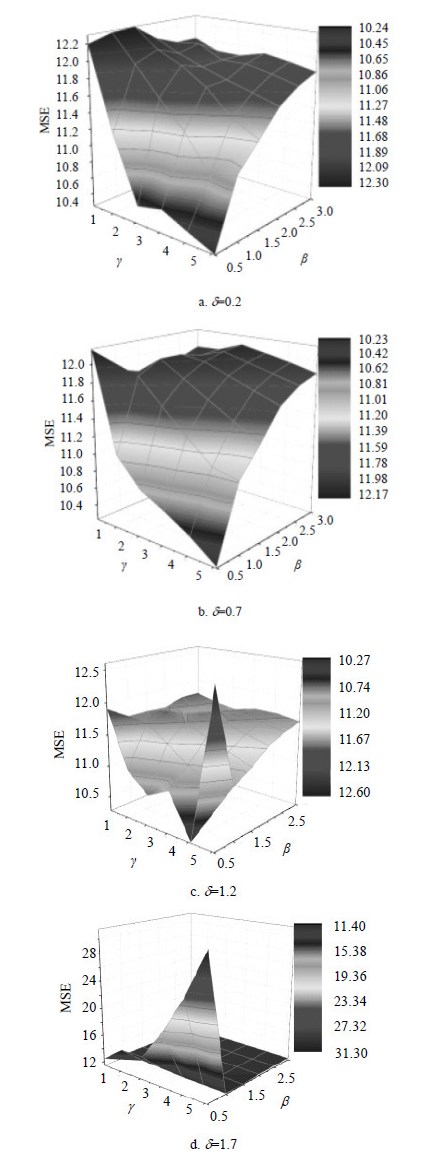 |
| 图3 AAT-HO3M在n=2时预测误差随参数变化图 |
当阶数 $ n=3 $ 时:
AAT-HO3M预测误差MSE随参数$ \gamma $、$ \beta $的变化曲线如图 4所示。取$ \delta =0.2 $,如图 4a所示,当$ \gamma =5.1 $,$ \beta =0.5 $时,预测误差最小,为$ \text{MES = 10}\text{.244 9} $。取$ \delta =0.7 $,如图 4b所示,当$ \gamma =5.1 $,$ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 9}\text{.433 9} $。取$ \delta =1.2 $,如图 4c所示,当 $ \text{MES = 11}\text{.185 1} $,$ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 11}\text{.185 1} $。取$ \delta =0.2 $,如图 4d所示,当$ \gamma =5.1 $,$ \beta =0.5 $时,预测误差最小,为 $ \text{MES = 10}\text{.277 4} $。由此可见当阶数$ n=3 $时,$ \delta =0.7 $,$ \gamma =5.1 $,$ \beta =0.5 $,AAT-HO3M的预测误差最小,预测效果最好。
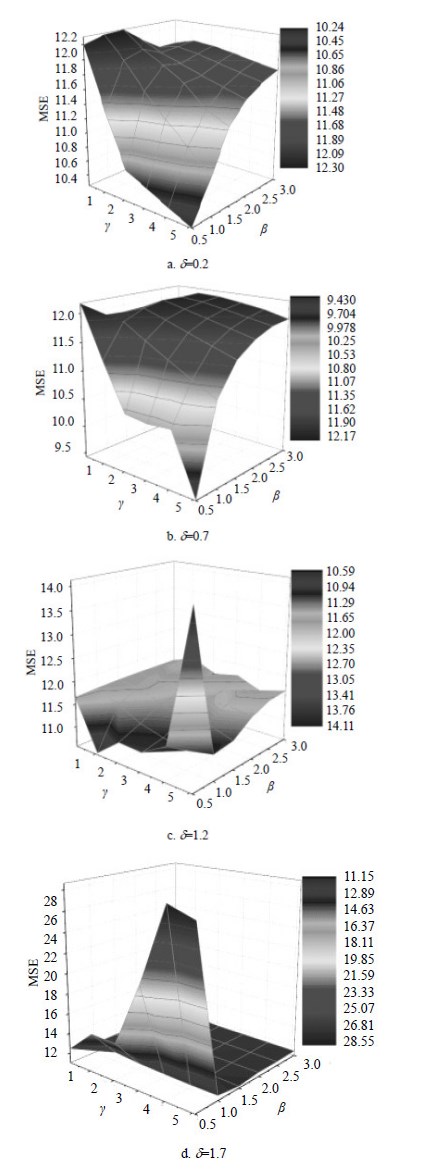 |
| 图4 AAT-HO3M在n=3时预测误差随参数变化图 |
进一步,给出AAT-HO3M在不同阶数下,取最优参数时,计算时间变化趋势如图 5所示,预测精度变化趋势如图 6所示。
 |
| 图5 AAT-HO3M在不同阶数下计算时间变化趋势图 |
 |
| 图6 AAT-HO3M在不同阶数下预测精度变化趋势图 |
从以上两幅图可以看到随着预测模型阶数的增加,预测精度提高,计算成本变高。
综合图 2~图 6可知,通过调节AAT-HO3M的参数来提升预测精度是有效的。
3 结束语本文提出的基于复杂城市道路网络的AAT-HO3M既反映了一条道路各时间点数据之间的相互影响,又考虑了各相关道路数据列之间的关联关系,这种混合预测的模式,更加接近城市交通网络的复杂情况,因而做出的预测更加符合现实。本文在改进模型的基础上引入多个参数,使得预测精度更高,预测效率更优。模型还可以通过调节参数,进一步提高模型预测精度。由于论文只涉及3周数据,实验数据集较小,但在实际应用中,可以根据不同情况通过收集更多的数据来验证预测模型的预测精度和预测效率,这不影响模型的实用价值。AAT-HO3M即可以用于复杂交通路口各相关道路的拥堵预测,也可以用于在整个交通网络下对各条道路的拥堵预测。这一研究结果为城市道路交通拥堵预测提供了一种新的方法。
本文研究工作得到成都师范学院科研项目(CS14ZB02)的支持,在此表示感谢。
| [1] | RICE J, ZWETE V. A simple and effective method for predicting travel times on freeways[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(3): 200-207. |
| [2] | HORVITZE J, APACIBLE J, SARIN R, et al. Prediction, expectation, and surprise: Methods, designs, and study of a deployed traffic forecasting service[C]//Proceedings of the Twenty-First Conference on Uncertainty in Artificial Intelligence. Edinburgh: [s.n.], 2005: 275-283. |
| [3] | STEPHANEDES Y J, MICHALOPOULOS P G, PLUM R A. Improved estimation of traffic flow for real-time control[C]//Proceedings of The 60th Annual Meeting of the Transportation Research Board. Washington: Transportation Research Board, 1981: 28-39. |
| [4] | DOUGHERTY M S, KIRBYHR, BOYLE R D. The use of neural networks to recognizeand predict trafficcongestion[J]. Trafic Engineering and Control, 1993, 34(6): 311-314. |
| [5] | CHINGWK, FUNG E S, NG MK. A multivariate Markov chain model for categorical data sequences and its applications in demand predictions[J]. IMA Journal of Management Mathematics, 2002,13(3): 187-199. |
| [6] | CHING W K, FUNG E S, NG MK. Higher-order Markovchain models for categorical data sequences[J]. Naval Research Logistics, 2004, 51(4): 557-574. |
| [7] | CHING W K, SIU T, LI L. An improved parsimonious multivariate Markov chain model for credit risk[J]. Journal of Credit Risk, 2009, 5(1): 1-25. |
| [8] | CHING W K. Iterative methods for queuing and manufacturing systems[M]. London: Springer, 2001. |
| [9] | CHING W K. A higher-order Markov model for the newsboy's problem[J]. Journal of Operational Research Society, 2003, 54: 291-298. |
| [10] | CHING W K, FUNG E S, NG MK. Higher-order hidden Markov models with applications to DNA sequences[C]//Intelligent Data Engineering and Automated Learning. Heidelberg: Springer, 2003: 535-539. |
| [11] | CHING W K, NG MK, WONG K. Hidden Markov models and their applications to customer relationship management[J]. IMA Journal of Management Mathematics, 2004, 15(1): 13-24. |
| [12] | CHING W K, SCHOLTES S, ZHANG S. Numerical algorithms for dynamic traffic demand estimation between zones in a network[J]. Engineering Optimization, 2004, 36(3): 379-400. |
| [13] | SIU T K, CHING W K, FUNG E S, et al. Extracting information from spot interest rates and credit ratings using double higher-order hidden Markov models[J]. Computational Economics, 2005, 26(3): 69-102. |
| [14] | CHING W K, ZHANG S, NG MK. An approximation method for solving the steadys-tate probability distribution of probabilistic Boolean networks[J]. Bioinformatics, 2007, 23(12): 1511-1518. |
| [15] | CHING WK, FUNG ES, NG MK, et al. Interactive hidden Markov models and their applications[J]. IMA Journal of Management Mathematics, 2007, 18(1): 85-97. |
| [16] | CHING W K, SIU T, LI L. Modeling default data via an interactive hidden Markov model[J]. Computational Economics, 2009, 34(1): 1-19. |
| [17] | GU J, CHING WK, SIU T. On infectious models for dependent default risk[C]//The 4th In-ternational Joint Conference on Computational Sciences and Optimization. Yunnan: [s.n.], 2011: 1196-1200. |
| [18] | CHENX, CHING W K, CHEN X S, et al. Construction of probabilistic Boolean networks from a prescribed transition probability matrix: a maximum entropy rate approach[J]. East Asian Journal of Applied Mathematics, 2011, 1: 132-154. |
| [19] | CHING W K, CHEN X, CONG Y, et al. A maximum entropy rate approach for the construction of probabilistic Boolean networks from a prescribed transition probability matrix[J]. East Asian Journal of Applied Mathematics, 2011(1): 132-154. |
| [20] | KIJIMA M, MUROMACHI Y. Evaluation of credit risk of a portfolio with stochastic interest rate and default processes[J]. Journal of Risk, 2000(3): 5-36. |
| [21] | LI D. On default correlation: a copula function approach[J]. Journal of Fixed Income, 2000, 9(4): 43-54. |
| [22] | FREY R, MCNEIL A J. Dependent defaults in models of portfolio credit risk[J]. Journal of Risk, 2003(6): 59-92. |
| [23] | DUFFIE D, ECKNER A, HOREL G, et al. Frailty correlated default[J]. The Journal of Finance, 2009, 64(5): 2089-2123. |
| [24] | XI X J, MAMON R, DAVISON M. A higher-order hidden Markov chain-modulated model for asset allocation[J]. Journal of Mathematical Modelling and Algorithms in Operations Research, 2014, 13(1): 59-85. |
| [25] | GIORDANO J O, KALANTARI A S, FRICHE P M, et al. A daily herd Markov-chain model to study the reproductive and economic impact of reproductive programs combining timed artificial insemination and estrus detection[J]. Journal of Dairy Science, 2012, 95(9): 5442-5460. |
| [26] | HUANG X, XU N, BIGAARD S. A class of Markov chain models for average run length computations for autocorrelatedprocesses[J]. Communications in Statistics-Simulation and Computation, 2013, 42(7): 1495-1513. |
| [27] | QIANG Y G, MING H J, SHUI Z C, et al. Short-term traffic flow forecasting based on Markov chain model[C]//Intelligent Vehicles Symposium. Columbus: [s.n.], 2003: 208-212. |
| [28] | WANG C, HUANG T Z. A new improved parsimonious multivariate Markov chain model[J]. Journal of Applied Mathematics, 2013(4): 924-970. |
| [29] | CHING W K, NG MK, FUNG E S. Higher-order multivariate Markov chains and their applications[J]. Linear Algebra and its Applications, 2008, 428: 492-507. |
| [30] | YONG Z Y, WANG C L. A concept of nonlinear block diagonal dominance[J]. Journal of Computational and Applied Mathematics, 1997, 83: 1-10. |
| [31] | 北京市质量技术监督局. DB11/T 785-2011. 城市道路交 通运行评价指标体系[S]. 北京: 中国标准出版社, 2011. Beijing Bureau of Quality and Technical Supervision. DB11/T 785-2011. Urban road traffic performance index[S]. Beijing: Standards Press China, 2011. |
| [32] | NIELSEN T S, JOENSEN A. A new referencefor wind powerforecasting[J]. Wind Energy, 1998(1): 29-34. |
 2016, Vol. 45
2016, Vol. 45
