2. 广西师范大学数学与统计学院 广西 桂林 541004
2. College of Mathematics and Statistics, Guangxi Normal University Guilin Guangxi 541004
自美国物理学家发现玻色-爱因斯坦凝聚[1, 2, 3] ( Bose-Einstein condensate,BEC)现象以来,研究者在原子BEC体与光场的相互作用方面获得了大量的研究成果[4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]。原子BEC体有隧穿、宏观相干和量子超流性等奇异特性,在量子计算机、原子芯片和原子激光等领域都具有重要的应用价值。
本文在改进文献[16]中哈密顿量的基础上,对二能级原子玻色-爱因斯坦凝聚与二项式光场相互作用系统中原子激光的压缩性质进行了研究。原子激光出现了量子Rabi振荡现象并被周期性压缩,其振荡频率和最大压缩深度主要依赖于光场和原子间的相互作用强度$\varepsilon $,并且随$\varepsilon $的增大而增大。
1 改进的模型和求解在Bogoliubov近似下[17],文献[16]中的哈密顿量可表示为:
| $\begin{align} & H=({{\omega }_{0}}+2{{N}_{0}}\Omega ){{b}^{+}}b+\omega {{a}^{+}}a+ \\ & \varepsilon \sqrt{{{N}_{0}}}({{a}^{+}}b{{\text{e}}^{i\theta }}+a{{b}^{+}}{{\text{e}}^{-i\theta }})+N_{0}^{2}\Omega \\ \end{align}$ | (1) |
根据文献[18]的分析,可知式(1)中$\Omega $对应于${{u}_{0}}/(2{{N}_{0}})$,可将式(1)改写为:
| $\begin{matrix} H=({{\omega }_{0}}+{{u}_{0}}){{b}^{+}}b+\omega {{a}^{+}}a+ \\ \varepsilon \sqrt{{{N}_{0}}}({{a}^{+}}b{{\text{e}}^{i\theta }}+a{{b}^{+}}{{\text{e}}^{-i\theta }})+\frac{1}{2}{{u}_{0}}{{N}_{0}} \\ \end{matrix}$ | (2) |
通过比较式(1)和式(2)可知,本文改进后的哈密顿量与文献[16]的哈密顿量有两点区别:1) 文献[16]中哈密顿量第一项的能级间隔${{\omega }_{0}}+2{{N}_{0}}\Omega $,增加量$\Delta =2{{N}_{0}}\Omega $与BEC中的原子数${{N}_{0}}$和原子间的相互作用强度$\Omega $的乘积成正比,即哈密顿量的能级间隔与原子间的相互作用强度$\Omega $有关,而本文改进后的哈密顿量第一项的能级间隔${{\omega }_{0}}+{{u}_{0}}$,增加量$\Delta ={{u}_{0}}$与原子间相互作用强度$\Omega $无关;2) 文献[16]中哈密顿量第四项$N_{0}^{2}\Omega $与原子间的相互作用强度$\Omega $有关,而本文改进后的哈密顿量中第四项${{u}_{0}}{{N}_{0}}/2$只与BEC中的原子数${{N}_{0}}$有关,与原子间的相互作用强度$\Omega $无关。这说明文献[16]中的哈密顿量与原子间的相互作用强度$\Omega $有关,具有一定的局限性;而通过本文改进后的哈密顿量与原子间的相互作用强度$\Omega $无关,更具有普遍性。
在非共振条件下,求解系统的海森堡运动方程为:
| $i\dot{a}=[a,H]=\omega a+\varepsilon \sqrt{{{N}_{0}}}b{{\text{e}}^{\text{i}\theta }}$ | (3) |
| $i\dot{b}=[b,H]=\varepsilon \sqrt{{{N}_{0}}}a{{\text{e}}^{-\text{i}\theta }}+({{\omega }_{0}}+{{u}_{0}})b$ | (4) |
| $a(t)=\frac{{{\text{e}}^{-\text{i}(\omega +{{\omega }_{0}}+{{u}_{0}})t/2}}}{\gamma }\left\{ \left[ \gamma \cos (\gamma t)-i\frac{\omega -{{\omega }_{0}}-{{u}_{0}}}{2}\times \sin (\gamma t) \right]a(0)-i\sqrt{{{N}_{0}}}\varepsilon \sin (\gamma t){{\text{e}}^{\text{i}\theta }}b(0) \right\}$ | (5) |
| $b(t)=\frac{{{\text{e}}^{-\text{i}(\omega +{{\omega }_{0}}+{{u}_{0}})t/2}}}{\gamma }\left\{ -i\sqrt{{{N}_{0}}}\varepsilon \sin (\gamma t){{\text{e}}^{-\text{i}\theta }}a(0)+\left[ \gamma \cos (\gamma t)+i\frac{\omega -{{\omega }_{0}}-{{u}_{0}}}{2}\sin (\gamma t) \right]b(0) \right\}$ | (6) |
二项式光场[19]定义为:
| $\left| \eta M \right\rangle =\sum\limits_{n=0}^{M}{C_{n}^{M}\left| n \right\rangle \begin{matrix} {} & 0 < \eta < 1 \\ \end{matrix}}$ |
原子激光的两个缓变正交分量算符为[20]:
| ${{U}_{1}}=\frac{1}{2}(b{{\text{e}}^{\text{i}\omega t}}+{{b}^{+}}{{\text{e}}^{-\text{i}\omega t}})$ | (7) |
| ${{U}_{2}}=\frac{1}{2i}(b{{\text{e}}^{\text{i}\omega t}}-{{b}^{+}}{{\text{e}}^{-\text{i}\omega t}})$ | (8) |
| ${{Q}_{i}}={{(\Delta {{U}_{i}})}^{2}}-1/4$ | (9) |
| ${{Q}_{1}}(t)=\frac{{{\varepsilon }^{2}}}{2({{\varepsilon }^{2}}+u_{0}^{2}/2)}{{\sin }^{2}}(\gamma t)\times \left\{ \begin{align} & \sum\limits_{n=0}^{M}{[C_{n}^{2}n-{{C}_{n}}{{C}_{n+2}}\sqrt{(n+2)(n+1)}\times }\cos ({{u}_{0}}t)]- \\ & {{\left( \sum\limits_{n=0}^{M}{{{C}_{n}}{{C}_{n+1}}}\sqrt{n+1} \right)}^{2}}[1-\cos ({{u}_{0}}t)] \\ \end{align} \right\}$ | (10) |
由于${{Q}_{1}}(t)$和${{Q}_{2}}(t)$具有对称性,本文只对${{Q}_{1}}(t)$进行数值分析,如图 1所示。
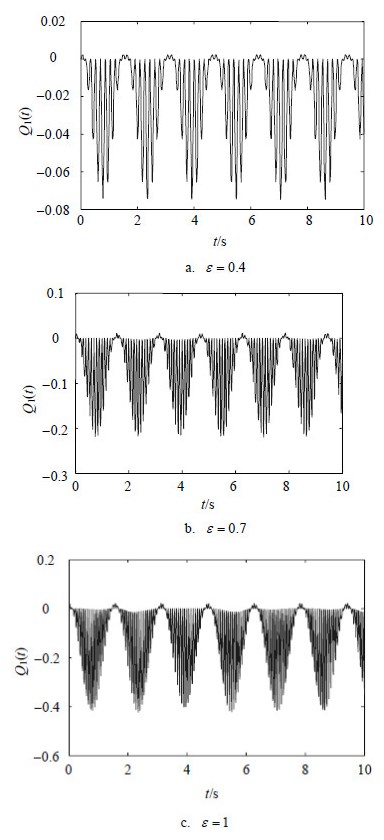 |
| 图1 ${{Q}_{1}}(t)$随$\varepsilon $变化的时间演化曲线 (${{N}_{1}}=2\text{ }000$,${{u}_{0}}=4$,$M=5$,$\eta =0.4$) |
从图 1可以看出,原子激光的两正交分量的涨落均出现周期性压缩,并且具有量子Rabi振荡。当保持光场参数$M$和场模参数$\eta $不变时,量子Rabi振荡频率和最大压缩深度均随$\varepsilon $的增大而增大。对于文献[16],当$\varepsilon $较小时,${{Q}_{1}}(t)$呈现周期性变化较明显;当$\varepsilon $较大时,${{Q}_{1}}(t)$呈现类似混沌的行为;而本文中${{Q}_{1}}(t)$都呈现明显的周期性变化。在相同条件下,文献[16]中原子激光的压缩效果较差,最大压缩深度约为-0.005,而本文中的原子激光的压缩效果较好,几乎完全压缩,且最大压缩深度约为-0.08,是文献[16]中原子激光最大压缩深度的16倍。
3 结束语本文在改进文献[16]中哈密顿量的基础上,对二能级原子玻色-爱因斯坦凝聚与二项式光场相互作用系统中原子激光的压缩性质进行了研究。 原子激光出现量子Rabi振荡现象且能被周期性压缩,其振荡频率和最大压缩深度主要依赖于光场和原子间的相互作用强度。
| [1] | ANDERSON M H, ENSCHER J R, METHEWS M R, et al. Observation of Bose-Einstein condensation in a dilute atomic vapor[J]. Science, 1995, 269(5221): 198-201. |
| [2] | DAVIS K B, MEWES M O, ANDREWS M R, et al. Bose-Einstein condensation in a gas of sodium atoms[J]. Physical Review Letter, 1995, 75(22): 3969-3973. |
| [3] | MEMES M O, ANDREWS M R, KURN D M, et al. Output coupler for Bose-Einstein condensed atoms[J]. Physical Review Letter, 1997, 78(4): 582-584. |
| [4] | YOU L, LEWENSTEIN M, COOPER J. Quantum field theory of atoms interacting with photons[J]. Physical Review A, 1995, 51(6): 4712-4727. |
| [5] | JING Hui, CHEN Jing-ling, GE Mo-lin. Quantumdynamical theory for squeezing the output of a Bose-Einstein condensate[J]. Physical Review A, 2001, 63(1): 015601-015604. |
| [6] | KUANG Le-man, ZHOU Lan. Generation of atom-photon entangled states in atomic Bose-Einstein condensate via electromagnetically induced transparency[J]. Physical Review A, 2003, 68(4): 043606-043614. |
| [7] | ZHENG Gong-ping, LIANG Jiu-qing, LIU Wu-ming. Phase diagram of two-species Bose-Einstein condensates in an optical lattice[J]. Physical Review A, 2005, 71(5): 053608-053612. |
| [8] | XIE Zheng-wei, CAO Ze-xian, KATS E I, et al. Nonlinear dynamics of a dipolar Bose-Einstein condensate in an optical lattice[J]. Physical Review A, 2005, 71(2): 025601-025604. |
| [9] | JI An-chun, LIU Wu-ming, SONG Jun-liang, et al. Dynamical creation of fractionalized vortices and vortex lattices[J]. Physical Review Letter, 2008, 101(1): 010402-010405. |
| [10] | 李明, 陈鼎汉. 光场-原子BEC相互作用系统中的压缩 特性[J]. 电子科技大学学报, 2011, 40(4): 541-543. LI Ming, CHEN Ding-han. Squeezing properties of light field interacting with Bose-Einstein condensate of atoms[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(4): 541-543. |
| [11] | 李明. 原子玻色-爱因斯坦凝聚体对V型三能级原子激 光压缩性质的影响[J]. 物理学报, 2011, 60(6): 063201. LI Ming. Influence of an atomic Bose-Einstein condensate on the squeezing properties of V-type three-level atomic lasers[J]. Acta Physica Sinica, 2011, 60(6): 063201. |
| [12] | 李明, 唐涛, 陈鼎汉. V型三能级原子双模光场系统中光 场压缩性质[J]. 物理学报, 2011, 60(7): 073203. LI Ming, TANG Tao, CHEN Ding-han. Squeezing properties of two-mode squeezed field interacting with V-type three-level atoms[J]. Acta Physica Sinica, 2011, 60(7): 073203. |
| [13] | 李明, 陈鼎汉, 陈翠玲. Ξ型三能级原子玻色-爱因斯坦 凝聚体对光场压缩性质的影响[J]. 物理学报, 2013, 62(18): 183201. LI Ming, CHEN Ding-han, CHEN Cui-ling. Influence of Ξ-type three-level atomic Bose-Einstein condensate on the squeezing properties of light field[J]. Acta Physica Sinica, 2013, 62(18): 183201. |
| [14] | 李明, 陈翠玲. 二能级原子玻色-爱因斯坦凝聚体与双 模光场相互作用系统中原子激光的压缩性质[J]. 物理学 报, 2014, 63(4): 043201. LI Ming, CHEN Cui-ling. Squeezing properties of atom laser from two-level atomic Bose-Einstein condensate interacting with two-mode light field[J]. Acta Physica Sinica, 2014, 63(4): 043201. |
| [15] | 农春选, 李明, 陈翠玲. Ξ型三能级原子玻色-爱因斯坦 凝聚体单模光场系统中双模原子激光的压缩性质[J]. 物 理学报, 2014, 63(4): 043202. NONG Chun-xuan, LI Ming, CHEN Cui-ling. Squeezing properties of two-mode atom laser in a system of Ξ-type three-level atomic Bose-Einstein condensate interacting with single-mode light field[J]. Acta Physica Sinica, 2014, 63(4): 043202. |
| [16] | 宫艳丽, 萨楚尔夫, 崔英华. 玻色-爱因斯坦凝聚与二项 式光场相互作用系统中的压缩特性[J]. 内蒙古师范大学 学报, 2007, 36(5): 605-609. GONG Yan-li, SACHUERFU, CUI Ying-hua. The squeezing properties of the binomial states field interacting with atomic Bose-Einstein condensate[J]. Journal of Inner Mongolia Normal University, 2007, 36(5): 605-609. |
| [17] | 倪光炯, 陈苏卿. 高等量子力学[M]. 上海: 复旦大学出 版社, 2000. NI Guang-jiong, CHEN Su-qing. Advanced quantum mechanics[M]. Shanghai: Fudan University Press, 2000. |
| [18] | 李明, 孙久勋. 原子间相互作用对光场和原子激光压缩 性质的影响[J]. 物理学报, 2006, 55(6): 2702-2707. LI Ming, SUN Jiu-xun. Influence of the interaction between atoms on the squeezing of light field and atomic lasers[J]. Acta Physica Sinica, 2006, 55(6): 2702-2707. |
| [19] | 王晓光, 于荣金, 李文. 位移二项式态与位移负二项式 态的性质及其与二能级原子的相互作用[J]. 物理学报, 1998, 47(11): 1798-1803. WANG Xiao-guang, YU Rong-jin, LI Wen. The properties of displaced binomial states and displaced negative binomial states and their interaction with two-level atoms[J]. Acta Physica Sinica, 1998, 47(11): 1798-1803. |
| [20] | 彭金生, 李高翔. 近代量子光学导论[M]. 北京: 科学出 版社, 1996. PENG Jin-sheng, LI Gao-xiang. Introduction of modern quantum optics[M]. Beijing: Science Press, 1996. |
 2016, Vol. 45
2016, Vol. 45
