内模控制是由文献[1]提出的一种性能优越的控制方法,它具有设计简单、调节性能好、鲁棒性强以及消除不可测干扰的影响等优点[2, 3]。由于实际系统大多是非线性的,需要设计非线性的内模控制方法,目前应用最广泛的是神经网络和支持向量机两种方法。基于神经网络[2, 4]的内模控制系统,利用输入输出数据可以获得未知非线性系统的神经网络模型,但是神经网络的训练一般采用梯度算法,收敛慢且容易陷入局部最小,神经网络结构难以选择。基于结构风险最小化的支持向量机[5, 6],在一定程度上克服了传统非线性建模的近似线性,能有效克服局部极小点、过学习等缺陷,但是对大规模训练样
本难以实施,训练速度也较慢。ELM[7, 8]是一种网络结构简单、学习速度快的前馈神经网络。利用Moore- Penrose广义逆求解网络输出层权重,可获得较小的权重范数和泛化性能。但是基本的极限学习机却存在模型参数不稳定的缺点,输入权值和阈值的随机设定容易造成过拟合或训练不充分的问题。
本文将L1和L2范数罚函数引入极限学习机模型,并提出MELM算法。将这种改进的极限学习机用于构造内模控制系统,并用于典型的非线性系统中。通过与极限学习机和最小二乘支持向量机两种方法的对比,分析基于改进极限学习机的内模控制系统在控制性能、抗干扰能力和鲁棒性能方面的优势。
1 极限学习机的算法描述 1.1 极限学习机的基本原理ELM是由文献[9]提出的一种新型单隐含层前馈神经网络,由于其具有全局逼近能力,参数学习不需迭代以及速度明显快于现有的神经网络和支持向量机等特点,其改进算法和实际应用引起了广泛的关注[10]。极限学习机的模型可以描述为:
| $\mathbf{y}=f(\mathbf{x})=\sum\limits_{i=1}^{L}{{{\mathbf{\beta }}_{i}}}g(\mathbf{x};{{\mathbf{w}}_{i}},{{b}_{i}})$ | (1) |
| $g(\mathbf{x};{{\mathbf{w}}_{i}}\text{,}{{b}_{i}})=g({{\mathbf{w}}_{i}}\mathbf{x}\text{+}{{b}_{i}})$ | (2) |
若采用RBF形式的隐层节点,那么激活函数模型可描述为:
| $g(\mathbf{x};{{\mathbf{w}}_{i}},{{b}_{i}})=g(\frac{\left\| \mathbf{x}-\mathbf{w}_{i}^{\text{T}} \right\|}{{{b}_{i}}})$ | (3) |
ELM中除了${{\mathbf{\beta }}_{i}}$其他参数都是随机产生的。对于给定的$N$个样本$\{{{x}_{i}},{{y}_{i}}\}$,代入式(1)有:
| $\mathbf{H\beta }=\mathbf{Y}$ | (4) |
| $\mathbf{H}={{\left[ \begin{matrix} g({{\mathbf{w}}_{1}}{{\mathbf{x}}_{1}}+{{b}_{1}}) & g({{\mathbf{w}}_{2}}{{\mathbf{x}}_{1}}+{{b}_{2}}) & \cdots & g({{\mathbf{w}}_{L}}{{\mathbf{x}}_{1}}+{{b}_{L}}) \\ g({{\mathbf{w}}_{1}}{{\mathbf{x}}_{2}}+{{b}_{1}}) & g({{\mathbf{w}}_{2}}{{\mathbf{x}}_{2}}+{{b}_{2}}) & \cdots & g({{\mathbf{w}}_{L}}{{\mathbf{x}}_{2}}+{{b}_{L}}) \\ \vdots & \vdots & \ddots & \vdots \\ g({{\mathbf{w}}_{1}}{{\mathbf{x}}_{N}}+{{b}_{1}}) & g({{\mathbf{w}}_{2}}{{\mathbf{x}}_{N}}+{{b}_{2}}) & \cdots & g({{\mathbf{w}}_{L}}{{\mathbf{x}}_{N}}+{{b}_{L}}) \\ \end{matrix} \right]}_{N\times L}}$ | (5) |
| $\mathbf{\beta }=\left[ \begin{matrix} \mathbf{\beta }_{1}^{T} \\ \mathbf{\beta }_{2}^{T} \\ \vdots \\ \mathbf{\beta }_{L}^{T} \\ \end{matrix} \right]\mathbf{Y}=\left[ \begin{matrix} \mathbf{y}_{1}^{T} \\ \mathbf{y}_{2}^{T} \\ \vdots \\ \mathbf{y}_{L}^{T} \\ \end{matrix} \right]$ | (6) |
ELM的最小二乘模型可以描述为:
| $L(\mathbf{X},\mathbf{Y};\mathbf{\beta })={{\left\| \mathbf{Y}-\mathbf{H\beta } \right\|}^{2}}$ | (7) |
故极限学习机的训练过程等价于式(7)的最小二乘解:
| $\mathbf{\hat{\beta }}={{\mathbf{H}}^{\dagger }}\mathbf{Y}$ | (8) |
式中,${{\mathbf{H}}^{\dagger }}$为隐含层输出矩阵的Moore-Penrose广义逆。
1.2 正则极限学习机极限学习机具有强大的回归性能,能够获得全局最优解,且模型训练时间很短。然而在ELM求解的过程中,存在由于特征矩阵奇异化造成模型参数不稳定的问题。因此,为了增强ELM的稳定性,可以在ELM中加入${{L}_{2}}$范数的罚函数,构成正则极限学习机[11]。其模型为:
| $L(\mathbf{X},\mathbf{Y};\mathbf{\beta },{{\lambda }_{2}})={{\left\| \mathbf{Y}-\mathbf{H\beta } \right\|}^{2}}+{{\lambda }_{2}}{{\left\| \mathbf{\beta } \right\|}^{2}}$ | (9) |
| $\mathbf{\hat{\beta }}={{({{\mathbf{H}}^{T}}\mathbf{H}+{{\lambda }_{2}}\mathbf{I})}^{-1}}{{\mathbf{H}}^{T}}\mathbf{Y}$ | (10) |
正则极限学习机本质上是一种结构风险最小化模型,能够较好的权衡经验风险和结构风险,因而相比基本的极限学习机,具有更好的泛化性能。
2 改进的极限学习机基本的ELM算法的隐层节点数、输入权值和阈值都是随机生成的,这样使得矩阵H中产生冗余特征和无关特征。隐层节点数设置过多,容易造成过拟合,设置过少,又会使得ELM的训练不充分。这些问题都使得ELM对数据的回归效果欠佳。本文MELM算法在正则极限学习机的模型中加入L1范数的罚函数,形式为:
| $L(\mathbf{X},\mathbf{Y};\mathbf{\beta },{{\lambda }_{1}},{{\lambda }_{2}})={{\left\| \mathbf{Y}-\mathbf{H\beta } \right\|}^{2}}+{{\lambda }_{1}}{{\left\| \mathbf{\beta } \right\|}^{1}}+{{\lambda }_{2}}{{\left\| \mathbf{\beta } \right\|}^{2}}$ | (11) |
式(11)称为naïve elastic net模型[12] 。在特征矩阵的初始化过程中,先随机生成充分多的隐藏节点,并利用L1范数的罚函数对重要的隐藏节点进行筛选。同时,利用L2范数的罚函数解决特征矩阵的奇异化问题。该模型使得选出的隐藏节点的信息量相对充分且干扰小,相当于从多次随机初始化的含有较少的隐藏节点的特征矩阵中选出了一个最优特征矩阵,因而使ELM算法的性能得到提高。
式(11)的模型可以改写成:
| $L(\mathbf{X},{{\mathbf{Y}}^{*}};{{\mathbf{\beta }}^{*}},\lambda )={{\left\| {{\mathbf{Y}}^{*}}-{{\mathbf{H}}^{*}}{{\mathbf{\beta }}^{*}} \right\|}^{2}}+\lambda {{\left\| {{\mathbf{\beta }}^{*}} \right\|}^{1}}$ | (12) |
它是一个典型的Lasso模型,其中:
| ${{\mathbf{Y}}^*} = \left( \begin{gathered} {\mathbf{Y}} \hfill \\ {0_{N \times 1}} \hfill \\ \end{gathered} \right){\text{ }}{{\mathbf{H}}^*} = {(1 + {\lambda _2})^{ - 1/2}}\left( \begin{gathered} {\mathbf{H}} \hfill \\ \sqrt {{\lambda _2}} {I_{N \times N}} \hfill \\ \end{gathered} \right)$ | (13) |
| ${{\mathbf{\beta }}^{*}}=\sqrt{1+{{\lambda }_{2}}}\mathbf{\beta } ,\text{ } \lambda ={{\lambda }_{1}}/\sqrt{1+{{\lambda }_{2}}}$ | (14) |
式(11)等价于式(12)求得参数$\mathbf{\beta }$的稀疏解,从而实现了隐藏节点的筛选功能。式(12)的解可以采用最小角回归(LARS)算法[15]求得,且解为:
| ${{\mathbf{\beta }}^{*}}=\underset{{{\mathbf{\beta }}^{*}}}{\mathop{argmin}}\,L(\mathbf{X},{{\mathbf{Y}}^{*}};{{\mathbf{\beta }}^{*}},\lambda )$ | (15) |
由式(14)中${{\mathbf{\beta }}^{*}}=\sqrt{1+{{\lambda }_{2}}}\mathbf{\beta }$推出式(9)模型的解为:
| $\mathbf{\beta }={}^{{{\mathbf{\beta }}^{*}}}\!\!\diagup\!\!{}_{\sqrt{1+{{\lambda }_{2}}}}\;$ | (16) |
naïve elastic net模型通过引入两个罚函数,减少了模型的方差,但同时对回归系数造成了过多收缩,引入过多的偏倚。为了修正偏倚,需要对回归系数进行调整,即将naïve elastic net模型修正为elastic net模型 [13]:
| $\mathbf{\beta }(elstic net)=(1+{{\lambda }_{2}})\mathbf{\beta }(naive elstic net)$ | (17) |
elastic net模型中的非零参数${{\mathbf{\beta }}_{i}}$对应的隐藏节点就是关键节点。
3 基于极限学习机的内模控制 3.1 内模控制的系统结构在本文采用的内模控制设计方案中需要建立两个极限学习机模型,一个用于构造内部模型,另一个用来构造逆模型。基于改进极限学习机的内部模型如图 1所示,图中${{G}_{P}}$表示被控对象,${{G}_{M}}$为改进极限学习机的内部模型,${{G}_{IMC}}$是改进极限学习机的内模控制器,d为干扰,${{F}_{1}}$是滤波器,${{y}_{r}}$是系统的输入,${{y}_{k}}$是系统的输出。
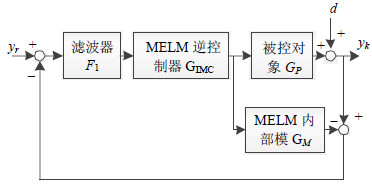 |
| 图1 改进极限学习机内模控制框图 |
内模控制系统的输出为:
| ${{y}_{k}}=\frac{{{G}_{IMC}}{{G}_{P}}}{1+{{G}_{IMC}}({{G}_{P}}-{{G}_{M}})}({{y}_{r}}-d)+d$ | (18) |
假如有如下单输入单输出非线性系统模型:
| $\begin{align} & y(k+1)=f(y(k),y(k-1),\cdots ,y(k-n), \\ & u(k),u(k-1),\cdots ,u(k-m)) \\ \end{align}$ | (19) |
式中,y为系统输出;u为系统输入;n为系统阶次;m为输入延迟;f为一非线性函数。设:
| $\begin{align} & X(k)=(y(k),y(k-1),\cdots ,y(k-n), \\ & u(k),u(k-1),\cdots ,u(k-m)) \\ \end{align}$ | (20) |
式中,$k=1,2,\cdots ,N$,则$\[y(k+1)=f(X(k))\]。对于极限学习机,只需要知道输入输出数据,构造训练样本集$(X(k),y(k+1))$并将其作为极限学习机的输入输出数据对,因此用极限学习机可建立起内部模型。
3.3 极限学习机建立的逆模型极限学习机建立起的被控对象的逆模型被用作内模控制器,并且要考虑到过程的可逆性问题。式(15)所描述的非线性系统,如果存在一个集合${{R}^{m+n+1}}$的子集A,当$[y(k),\text{ }y(k-1), \cdots ,\text{ }y(k-n),\text{ }u(k),\text{ }$$u(k-1), \cdots ,$$u(k-m)]\in A$时,对于任意两个不同输入${{u}_{1}}(k)$和${{u}_{2}}(k)$,都有:
| $\begin{matrix} f(y(k),y(k-1),\cdots ,y(k-n), \\ u(k),u(k-1),\cdots ,u(k-m))\ne \\ f(y(k),y(k-1),\cdots ,y(k-n), \\ \end{matrix}$ |
| ${{u}_{2}}(k),{{u}_{2}}(k-1),\cdots ,{{u}_{2}}(k-m))$ | (21) |
成立,则系统在$[y(k),y(k-1),\cdots ,y(k-n),u(k),u(k - 1), \cdots ,u(k - m)]$处是可逆的,并且如果式(18)对于$u(k)$是单调的,那么系统在$[y(k),y(k-1),\cdots ,$$y(k-n),u(k),u(k-1),\cdots ,u(k-m)]$处是可逆的[14]。
假设系统是可逆的,则用极限学习机方法建立的内部模型的逆模型就是所设计的控制器,即:
| $\begin{align} & u(k)={{f}^{-1}}({{y}_{k}}(k+1),y(k),y(k-1),\cdots ,y(k-n), \\ & u(k),u(k-1),\cdots ,u(k-m)) \\ \end{align}$ | (22) |
对于非线性控制,过程的逆模型往往很难得到,由于过程是可逆的,因此模型一定存在。本文采用极限学习机方法估计过程的逆模型。设:
| $\begin{align} & Y(k)=({{y}_{r}}(k+1),y(k),y(k-1),\cdots ,y(k-n), \\ & u(k),u(k-1),\cdots ,u(k-m)) \\ \end{align}$ | (23) |
式中,$k=1,2,\cdots ,N$,则$u(k)={{f}^{-1}}(Y(k))$。
构造训练样本集$(Y(k),u(k))$并将其作为极限学习机输入输出数据对,采用极限学习机建立内部模型的逆模型,并将该模型作为控制器。
3.4 极限学习机模型参数的作用及设置方法内模控制系统中,两个基于改进极限学习机的模型(即内部模型和外部模型)均是回归模型。改进的极限学习机模型,在训练前有两个参数需要提前设定,分别是惩罚系数${{\lambda }_{1}}$和${{\lambda }_{2}}$。系数${{\lambda }_{1}}$的作用是通过控制所选择的隐藏层节点的数目,实现特征的自动选择;系数${{\lambda }_{2}}$的作用是防止系统过拟合,提升系统模型的泛化能力。参数${{\lambda }_{1}}$和${{\lambda }_{2}}$通过交叉验证法确定。
4 内模控制器仿真分析 4.1 信号跟踪研究采用如下的非线性系统:
| $y(k+1)=\frac{0.6y(k)}{1+{{y}^{2}}(k)}+0.3u(k)y(k)+0.8u(k)$ | (24) |
容易证得该系统是单调的,故而该系统可逆。辨识信号采用幅值为2的随机信号,得到200组非线性系统的输入输出数据对。用极限学习机离线辨识该非线性系统的内部模型和逆模型。
将训练好的改进极限学习机的内部模型和逆模型与原系统复合构成内模控制系统,对复合系统的输入段分别施加各典型信号,检验其跟踪效果。
采用的典型信号包括:幅值为1的阶跃信号、正弦波信号$0.5sin(2\pi kts)+0.5$、方波信号$0.5sign(sin(2\times $ $\pi kts))+0.5$和锯齿波信号。MELM、ELM和LS-SVM对各信号的跟踪结果对比情况(以正弦波和方波为例)如图 2~图 4所示。采用均方根误差(RMSE)作为跟踪误差的评价指标,采用系统响应时间衡量各算法的计算复杂度,结果如表 1所示。
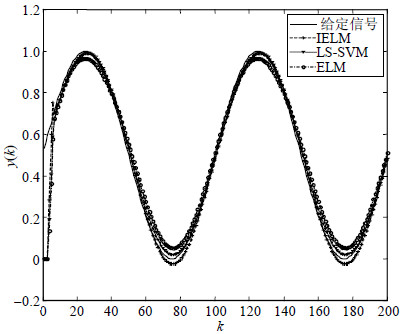 |
| 图2 正弦波信号跟踪结果 |
 |
| 图3 方波信号跟踪结果 |
 |
| 图4 正弦波信号抗扰跟踪结果 |
| 表1 典型信号跟踪误差(响应时间) |
从图 2和图 3可以看出,改进极限学习机对给定输入信号的跟踪精度高,响应速度快,动态性能好。表 1表明改进极限学习机的跟踪误差小于最小二乘支持向量机和基本的极限学习机,稳态性能更优。MELM的响应时间慢于ELM,略小于LS-SVM,但总的来说响应时间较快。
4.2 控制系统对外部不确定干扰的抑制能力非线性系统不可避免的存在测量噪声和外部干扰,为了检验内模控制的抗干扰特性,对输入信号施加干扰。假设在0.8s(k=80)时施加幅值为0.2的阶跃扰动,在1.3s(k=130)时施加幅值为-0.2的阶跃扰动,即:
| $d(k)=\left\{ \begin{array}{*{35}{l}} 0.2, & k=80 \\ -0.2, & k=130 \\ 0, & 其他 \\ \end{array} \right.$ | (25) |
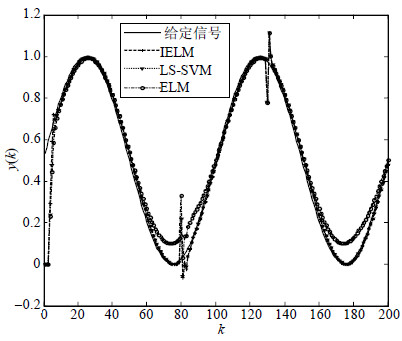
依然采用4种典型信号作为输入信号。本文实验选取均方根误差(RMSE)和系统响应时间作为衡量指标,其多次试验结果如表 2所示。跟踪结果选取两种如图 4和图 5所示。
| 表2 典型信号抗干扰均方根误差(响应时间) |
 |
| 图4 正弦波信号抗扰跟踪结果 |
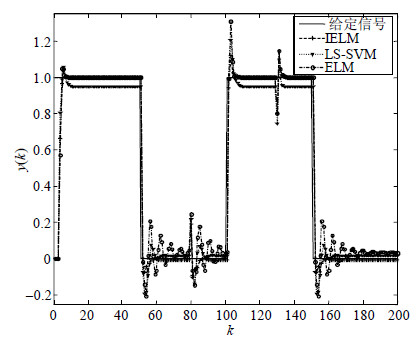 |
| 图5 方波信号抗扰跟踪结果 |
从图 4和图 5可以看出,在0.8s(k=80) 和1.3s(k=130)时,系统输出的误差增大。从表 2可以看出,所提出的基于改进极限学习机的内模控制系统,在有干扰信号情况下的均方根误差是最小的,LS-SVM其次,而ELM最大。但是在响应时间上,ELM最短,MELM其次,LS-SVM最长。表明改进极限学习机的内模控制系统有良好的鲁棒性,系统响应较快,对测量噪声和外部干扰等扰动有较强的抑制作用,使得控制系统能够较好地跟踪输入信号。
4.3 非线性系统参数发生变化时的鲁棒性为研究非线性系统的参数发生变化时,内模控制器的鲁棒性,假设$t>1.3\text{ }s(k>130)$时,原系统的参数发生变化,原系统变为:
| $y(k+1)=\frac{0.6y(k)}{1+{{y}^{2}}(k)}+0.1u(k)y(k)+0.6u(k)$ | (26) |
选取4种信号中跟踪难度最大的方波信号作为系统的输入信号,其跟踪结果和跟踪误差如图 6和图 7所示。
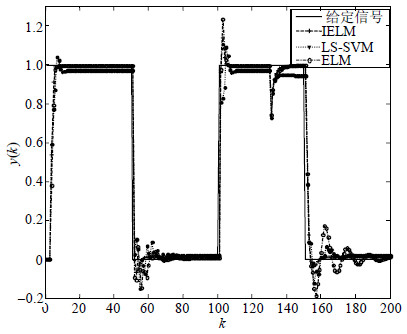 |
| 图6 方波信号参数变化的跟踪结果 |
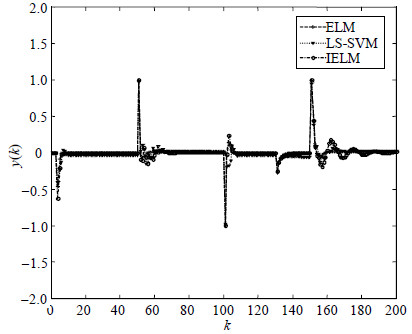 |
| 图7 方波信号参数变化的跟踪误差 |
从图 6和图 7可以看出,基于MELM的内模控制系统对系统参数的扰动具有较强的鲁棒性,跟踪精度优于极限学习机算法和最小二乘支持向量机。
5 结束语本文利用一种极限学习机算法用于逼近非线性系统的内部模型和逆模型,将内模控制和逆控制方法相结合,提出一种基于改进极限学习机算法的内模控制系统。在该系统中,不需要依赖控制对象太多的先验知识,只需要知道被控对象的输入输出数据就可以对非线性系统进行控制。通过一个典型的非线性系统进行控制仿真,对四种典型信号进行跟踪。在正常情况、系统存在干扰和系统参数发生变化3种情况下,基于改进极限学习机算法的内模控制系统具有更高的跟踪精度,系统的跟踪性能和鲁棒性能明显优于极限学习机算法和最小二乘支持向量机算法。因此,基于改进极限学习机的内模控制是一种有效的非线性系统的控制方法。
| [1] | ECONOMOU C G, MORARI E, PALSSON B O. Internal model control: Extension to nonlinear systems[J]. Industrial & Engineering Chemistry Process Design and Development, 1986, 25(25): 403-411. |
| [2] | ISABELLE R, LEON P. Nonlinear internal model control using neural networks: Application to processes with delay and design issues[J]. IEEE Transactions on Neural Networks, 2000, 11(1): 80-90. |
| [3] | DENG H, XU Z, LI H. A novel neural internal model control for multi-input multi-output nonlinear discrete-time processes[J]. Journal of Process Control, 2009, 19(8): 1392-1400. |
| [4] | LI H, DENG H. An Approximate internal model-based neural control for unknown nonlinear discrete processes[J]. IEEE Transactions on Neural Networks, 2006, 17(3): 659-670. |
| [5] | LIU G, CHEN L, ZHAO Wen-xiang, et al. Internal model control of permanent magnet synchronous motor using support vector machine generalized inverse[J]. IEEE Transactions on Industrial Informatics, 2013, 9(2): 890-898. |
| [6] | WANG Y, YUAN X. SVM approximate-based internal model control strategy[J]. ACTA Automatic Sinica, 2008, 34(2): 172-179. |
| [7] | HUANG G, ZHU Q, SIEW C K. Extreme learning machine: a new learning scheme of feed forward neural networks[C]//IEEE International Joint Conference on Neural Networks.[S.L.]: IEEE, 2004. |
| [8] | HONG J, WANG X. Training extreme learning machine via regularized correntropy criterion[J]. Neural Computing and Applications, 2013, 23(1): 1977-1986. |
| [9] | HUANG G, CHEN L, SIEW C K. Universal approximation using incremental constructive feed forward networks with random hidden nodes[J]. IEEE Transactions on Neural networks, 2006, 17(4): 879-892. |
| [10] | HUANG G, ZHU Q, SIEW C K. Extreme learning machine: Theory and applications[J]. Neurocomputing, 2006, 70(1): 489-501. |
| [11] | HUANG G, WANG D, LAN Y. Extreme learning machine: a survey[J]. International Journal of Machine Learning and Cybernetics, 2011(2): 107-122. |
| [12] | ZOU H, HASTIE T. Regularization and variable selection via the elastic net[J]. Journal of Computational and Graphical Statistics, 2006(15): 265-286. |
| [13] | SHI L, LU L. EEG-based vigilance estimation using extreme learning machines[J]. Neurocomputing, 2013(102): 135-143. |
| [14] | ZHANG W,MAO J. Internal model control for nonlinear system based on fuzzy-free method[J]. Control Theory & Applications, 2013, 30(4): 463-468. |
| [15] | EFRON B, HASTIE T, JOHNSTONE I, et al. Least angle regression[J]. Annals of Statistics, 2004, 32(2): 407-499. |
 2016, Vol. 45
2016, Vol. 45
