根据黑体辐射理论,温度高于绝对零度的物体都将向外产生热辐射,其强度与物体材料发射率及物理温度有关。被动毫米波成像技术利用聚焦天线结合高灵敏度辐射计接收机接收场景辐射的毫米波能量,根据不同物体间辐射能量强度差异实现成像[1]。由于毫米波具有穿透云雾、衣物等材料的能力,因此毫米波被动成像技术在机场等重要关口安检、场景监控等场合中有广泛的潜在应用[2, 3, 4]。
毫米波被动成像系统在应用于安检成像时,检测对象位于聚焦天线近场区域内,同时为提高成像速度,往往需要将多个馈源置于天线焦平面上构成焦平面阵列[5, 6]。这就要求系统的准光系统在特定的成像距离上形成最佳聚焦,且偏轴波束均匀性良好。
介质透镜天线由于具有无遮挡、损耗小、安装方式灵活等优点,被许多毫米波被动成像系统采用。作为被动成像系统的“眼睛”,透镜天线性能直接影响到系统的成像空间分辨率、亮温分辨率、成像景深等指标,是被动成像系统的关键部件之一。
透镜天线外形轮廓的优化设计是透镜天线设计的关键。透镜天线轮廓设计方法一般都是基于等光程原理,采用射线追踪方法优化得到[7, 8, 9, 10]。该方法设计理论简单,但设计精度一般,尤其在设计近程聚焦透镜时难以实现对聚焦波束束腰位置及束腰半径进行精确设计。
本文针对近场区域3 mm波焦平面阵列被动成像系统,完成了大口径介质透镜天线的设计。首先基于高斯波束法计算得到系统光路参数,然后采用光学软件ZEMAX对透镜天线外形轮廓优化设计,在此基础上利用近场仿真对设计结果进行验证与优化调整,实现了对透镜天线聚焦波束束腰位置及尺寸的精确设计,同时具有良好的偏轴波束均匀性,满足焦平面被动成像系统应用的需求。该方法提高了透镜天线设计效率,且设计精度高。
1高斯准光理论根据高斯准光理论,透镜天线近轴波束电场分布近似为高斯分布,其归一化表达式为[11]:
| $E(r,z) = \exp \left( { - \frac{{{r^2}}}{{{\omega ^2}(z)}}} \right)$ | (1) |
式中,r为场点偏离光轴的距离;z为距离透镜波束束腰位置的轴向距离;$\omega (z)$为z处的波束半径,即对应于波束场幅度降低到轴线上幅度的1/e时的半径值,其计算表达式为:
| $\omega (z) = {\omega _0}\sqrt {1 + {{\left( {\frac{{\lambda z}}{{{\rm{\pi }}\omega _0^2}}} \right)}^2}} $ | (2) |
| ${\omega _0} = \frac{{\omega (z)}}{2}\sqrt {1 - \sqrt {1 - {{\left( {\frac{{2\lambda z}}{{{\rm{\pi }}\omega _{}^2(z)}}} \right)}^2}} } $ | (3) |
式中,${\omega _0}$为束腰位置处的波束半径;$\lambda $为工作波长。可以推知,3 dB波束半径为高斯波束半径尺寸的约1.18倍。
高斯波束经透镜作用后,在另一侧形成的场分布仍然可以近似为高斯分布,即波束先在束腰位置处汇聚后再发散(如图 1所示)。
 |
| 图1 准光透镜高斯波束变换示意图 |
利用薄透镜变换关系,对于束腰位置距离透镜S1、半径为${\omega _{01}}$的高斯波束,变换后的聚焦波束束腰半径${\omega _{02}}$及位置${S_2}$可由下式求得[11]:
| ${\omega _{02}} = \frac{{{\omega _{01}}}}{{\sqrt {{{({S_1}/f - 1)}^2} + z_c^2/{f^2}} }}$ | (4) |
| ${S_2} = f + \frac{{{S_1} - f}}{{{{({S_1}/f - 1)}^2} + z_c^2/{f^2}}}$ | (5) |
式中,$f$为透镜焦距;${z_c} = {\rm{\pi }}\omega _0^2/\lambda $为透镜共焦距离。
由于透镜尺寸$D$有限,透镜高斯波束在透镜边缘被截断,透镜以外区域毫米波能量不能被接收,使天线效率降低。由式(1)可知,当透镜天线直径$D$与透镜处高斯波束半径$\omega $满足$D = 3\omega $时,透镜天线的截获效率为98.9%,满足工程应用要求[12]。
2 3 mm波被动成像系统光路设计 2.1 设计要求被动成像系统工作中心频率为89 GHz,要求在距离系统约3 m处的图像分辨率为30 mm,成像范围为700 mm×1 800 mm。
2.2 3 mm波被动焦平面成像系统光路设计要在距离系统3 m处实现30 mm图像分辨率,则要求透镜天线波束束腰位于距离系统3 m处,且3 dB焦斑尺寸不大于30 mm,相邻焦斑中心间距30 mm。
要实现700 mm×1 800 mm视场范围,可通过在透镜像方焦平面水平方向上放置24个天线单元组成焦平面线阵,实现在水平方向覆盖700 mm视场范围;垂直方向则采用机械扫描方式,在透镜与场景之间加入镜面反射器,通过镜面反射器周期扫描,覆盖1 800 mm场景。被动成像系统光路结构如图 2所示。
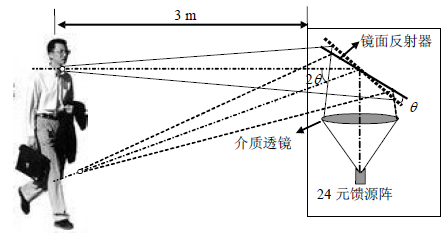 |
| 图2 3 mm波被动成像系统光路结构示意图 |
在系统光路中,镜面反射板的作用是改变光路传输路径。将其置于透镜与场景之间,当反射器转动$\theta $角度时,反射后的波束指向改变角度为$2\theta $,这样在覆盖场景区域固定的情况下可减小反射板转动角度范围,有利于实现快速扫描,实现3~5帧/s的系统成像速率。
考虑到部分光路被包含在系统内部,因此透镜设计时将透镜波束束腰位置确定于距离透镜3500mm处,以实现在距离系统3 m处获得最佳聚焦特性。
3 介质透镜天线的设计 3.1 透镜参数的确定透镜参数根据高斯准光理论确定。根据光学成像理论,物点通过透镜天线后将在像平面上形成爱里焦斑,相邻斑的间距与物点间距、物距、像距等有关。因此要在物平面上实现30mm分辨率,焦斑间距、物距、像距必须要合理选择并精心设计。
像平面上焦斑间距即为焦平面系统中接收馈源的间距。由于馈源口径以及辐射计接收通道物理尺寸均受限于馈源间距$d$,过小将限制辐射计通道尺寸使其难以实现,同时馈源口径尺寸受限导致馈源辐射波束展宽从而降低天线效率;过大则将导致对场景的采样密度不足,使成像效果恶化。
根据设计要求,透镜要在物距S1=3 500 mm处形成波束束腰,且其3dB聚焦焦斑尺寸${d_{{\rm{3dB}}}}$为30mm。由式(1)可求得该焦斑尺寸对应的波束束腰半径${\omega _{01}}$为12.8 mm,进而由式(2)求得$\omega $$ \approx $293 mm。
根据辐射计通道模块通道尺寸可实现性以及系统对场景采样要求,选择馈源间距$d$为6.1 mm。根据采样定理要求,相邻焦斑需交叠于3 dB位置,即透镜像平面上聚焦波束3 dB焦斑尺寸应为6.1 mm,对应波束束腰半径${\omega _{02}}$为2.6 mm。
将${S_1}$=3 500 mm,$\lambda $=3.37 mm,${\omega _{01}}$=12.7 mm,${\omega _{02}}$=2.6 mm代入式(4),确定$f$=592 mm时满足要求。进而由式(5)求得对应的聚焦点位置为${S_2}$≈712mm,即像距为712 mm。
3.2 馈源天线设计与效率分析在被动成像系统中,馈源被排成阵列置于透镜聚焦面上接收目标热辐射信号,因此馈源尺寸受限于馈源间距$d$,即小于6.1 mm。
本文采用矩形角锥喇叭天线作为馈源,经仿真优化,确定其口面尺寸$a \times b$=8.06 mm×5.8 mm,长度为10.4 mm。测试表明,该喇叭天线增益为16.2dB,E面和H面10 dB波束宽度分别为50°和52°,如图 3所示。
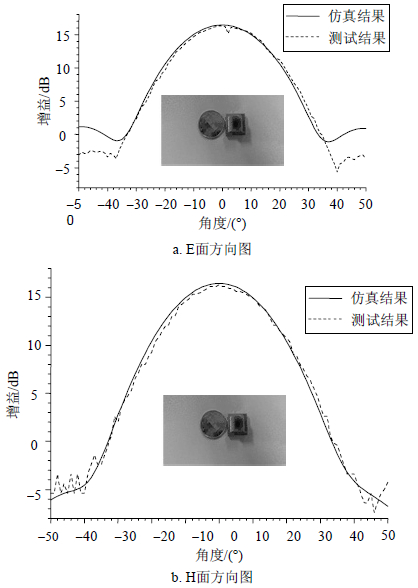 |
| 图3 喇叭馈源辐射方向图仿真与测试结果 |
喇叭天线辐射场不是理想高斯波束,其与透镜高斯波束间的耦合系数$c$可表示为:
| $c = \frac{{\left\langle {{E_{\rm{f}}}|{E_{\rm{G}}}} \right\rangle }}{{{{\left[{\left\langle {{E_{\rm{f}}}|{E_{\rm{f}}}} \right\rangle \left\langle {{E_{\rm{G}}}|{E_{\rm{G}}}} \right\rangle } \right]}^{0.5}}}}$ | (6) |
式中,$E{}_{\rm{f}}$为喇叭馈源口径场;$E{}_{\rm{G}}$为高斯波束场;$\left\langle {{f_1}|{f_2}} \right\rangle = \int {\int_s {{f_1}^ * {f_2}} } {\rm{d}}S$。将喇叭口径场近似为余弦分布,高斯波束展开为Gauss-Hermite模式,可得[13]:
| $\begin{array}{l} {c_m} = {\left[{\frac{2}{\pi }} \right]^{0.25}}{\left[{{2^m}m!} \right]^{ - 0.5}}{\left[{\frac{{\sqrt 2 s}}{\pi }} \right]^{0.5}} \times \\ \int_{ - \frac{\pi }{{2s}}}^{\frac{\pi }{{2s}}} {{H_m}(u)\exp \left( {\frac{{ - {u^2}}}{2}} \right)\cos (su){\rm{d}}u} \end{array}$ | (7) |
式中,$m$为高斯模阶数;${H_m}(u)$为$m$阶Hermite多项式,${H_0}(u) = 1$;$s = {\rm{\pi }}\omega /\sqrt 2 d$,$\omega $为高斯波束束腰半径,$d$为喇叭口径尺寸。
由式(7)可知,场耦合系数${c_m}$与高斯模阶数$m$及$s$有关,基模高斯波束($m = 0$)包含绝大部分能量[13],矩形喇叭口径场与基模高斯波束耦合系数${c_0}$随$s$变化,如图 4所示。由图可知,当$s$=0.78,即$\omega = 0.35d$时,${c_0}$达到最大值99.5%。
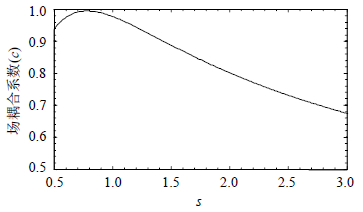 |
| 图4 喇叭馈源口径场与基模高斯波束间场耦合系数($s = {\rm{\pi }}\omega /\sqrt 2 d$) |
本文设计中,${\omega _{02}}$≈2.6 mm,所采用的馈源口径尺寸对应的$s$值分别为0.72和0.99,由图 4知,对应的基模高斯波束与馈源口径场间的一维耦合系数分别为0.991和0.978,功率耦合系数为|c0|2=0.9912×0.9782≈0.939。
3.3 介质透镜天线轮廓优化设计与仿真透镜天线结构一般为旋转轴对称,因此只要确定其截面曲线方程即可确定天线的轮廓。
在被动成像应用中,透镜天线的作用是将物平面上某点的辐射能量聚焦到像平面上,因此最简单的透镜天线轮廓设计方法是令其两侧表面都为具备聚焦特性的曲面(如双曲面),其焦距分别等于物距和像距。但这种方法设计的透镜难以保证聚焦位置、聚焦焦斑尺寸达到最优[10]。
本文采用光学设计与透镜天线近场仿真相结合的方法设计介质透镜天线。透镜天线采用双凸透镜,两侧曲面轮廓均选择为非球面,其方程为:
| $z = \frac{{{y^2}}}{{R + \sqrt {{R^2} - (1 + k){y^2}} }} + a{y^2} + b{y^4} + c{y^6} + d{y^8} + e{y^{10}}$ | (8) |
式中,$R$为曲面曲率半径;$k$为圆锥系数;$(y,z)$曲线点坐标;$a,b,c,d,e$为待定系数。
轮廓曲线方程中的待定系数由ZEMAX优化设计。ZEMAX是一款功能强大的综合性光学设计仿真软件,可以在实践中对所有光学系统进行设计、优化和分析。在软件中设定折射率(透镜材料)、物距、像距、口径尺寸、波长等设计参数,并确定优化目标后,即可对成像光路进行优化设计。
材料是透镜设计的要素之一,本文选用高密度聚乙烯(HDPE),其相对介电常数为2.3(折射率$n$约为1.517),介质损耗与聚四氟乙烯相近,但比重为约0.96,有利于减轻透镜天线重量。
在ZEMAX中新建折射率$n$为1.517的材料,以3.1节中所确定的物距、像距、透镜口径、波长等为预设参数,以聚焦波束尺寸及球差为优化目标,经过优化计算,ZEMAX自动给出满足要求的透镜轮廓曲线方程,式(8)中的各待定系数值即可确定。
由于ZEMAX是基于光学理论的设计软件,适用于可见光频段的光学系统设计与分析。将其用于毫米波频段的光学系统设计时,得到的设计结果还必须采用基于场的方法来进行仿真分析,验证结果正确性。本文采用FEKO对设计结果进行仿真验证。
首先将前述矩形喇叭天线在FEKO建模仿真,得到其远区辐射方向图并将结果保存为数据文件,作为透镜天线的馈电点辐射源输入。然后根据ZEMAX优化得到的透镜结构在FEKO中建立仿真模型,并将馈电点源位置设置在像平面上。由于透镜电尺寸较大(约为128$\lambda $),设定透镜区域求解方法为几何光学(GO)方法,以提高求解速度并降低对计算机内存的需求。
仿真结果显示,在ZEMAX中以物距${S_1}$=3500mm,像距${S_2}$=712 mm优化得到的透镜结构,在FEKO中仿真得到其聚焦波束束腰位置位于3 116 mm处,小于所需距离(3 500 mm)。为了实现物方波束束腰位置落在3 500 mm附近,对透镜轮廓进行反复优化,最终确定在ZEMAX中以物距${S_1}$=4 000 mm,像距${S_2}$=712 mm时优化得到的透镜,经FEKO仿真得到其波束束腰位置位于3 520 mm,聚焦焦斑尺寸${d_{{\rm{3dB}}}}$为26 mm,满足指标要求。
最终优化得到的透镜天线轮廓方程系数见表 1。
| 表1 透镜天线轮廓方程系数值 |
对近程毫米波成像系统而言,透镜天线最关键的参数是物方、像方聚焦波束束腰位置以及聚焦波束3 dB波束尺寸,前者分别决定成像系统的最佳成像距离及像平面所在位置,后者则决定系统的成像分辨率。
根据测试要求,搭建了专用的测试支架并搭建测试平台,如图 5所示。在发射端,矩形喇叭馈源连同W波段毫米波源模块置于支架上,支架可以沿水平、垂直、纵向3个方向平移;在接收端,W波段标准增益喇叭连同下变频谐波混频器置于支架上,支架置于3 m长滑轨上,同样可以沿水平、垂直、纵向3个方向平移。
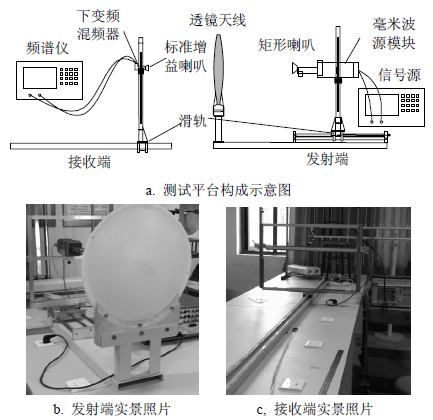 |
| 图5 透镜天线测试平台构成示意图及实景照片 |
由于系统工作于3 mm频段,测试支架的加工和安装精度要求较高。测试前,必须对测试平台进行细致调试,包括对轴调试以及平台水平性调试,以确保测试时,收、发端沿轴向移动时始终位于透镜的中心轴线上,沿水平方向横向移动时始终在同一水平面上。
测试时,首先将接收与发射端喇叭天线中心置于透镜中心轴线上,并使接收端天线位于距透镜3500mm,然后轴向移动发射端馈源,当接收到的信号最强时,发射馈源所在位置确定为像方聚焦波束束腰位置,这样即可测得物距为3 500 mm时对应的像距。
确定了成像系统的物距和像距后,将收、发天线分别在物平面、像平面上横向平移,即可测得聚焦波束的3 dB波束尺寸等性能参数。
4.2 测试结果与分析将接收端天线固定在距离透镜3 500 mm(物距)处,然后沿轴向移动发射端,测得当发射端天线距离透镜682 mm(像距)时,信号电平达到最大值。即透镜天线的物距为3 500 mm时,对应像距为682 mm。由透镜方程:
| $\frac{1}{f} = \frac{1}{{{S_i}}} + \frac{1}{{{S_o}}}$ | (9) |
求得透镜的实际焦距为571 mm,比设计值小21 mm。由于材料HDPE的折射率n与频率相关,其在89 GHz的真实值难以准确测得,设计值(n=1.517)与真实值存在误差,导致透镜实际焦距与设计值产生差异。
将发射端天线固定在像平面(682 mm)并位于中心轴线上,然后将接收端沿轴向移动,测得物方轴向归一化电平分布如图 6所示。结果表明,物方对应的电平最大值出现在距透镜天线约3 500 mm处,此处即为聚焦波束束腰所在位置。
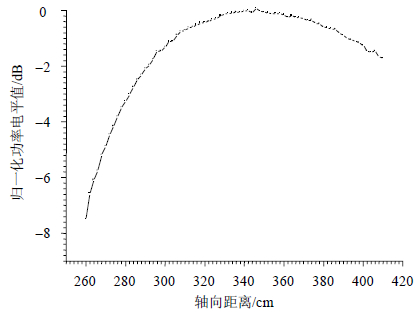 |
| 图6 物方轴向功率电平分布测试结果(${S_i}$=682 mm) |
物平面和像平面上聚焦焦斑尺寸及聚焦波束均匀性,是焦平面阵列天线的关键指标。将收、发天线分别固定在物平面和像平面上,并使接收端天线在物平面内以30 mm间隔依次横向偏移,模拟间距30 mm物点。然后在像平面内以1 mm步进横向移动发射天线并记录接收功率电平值,即可测得像平面上的聚焦波束焦斑尺寸及分布。物方天线偏离0、30、…、300 mm时像平面上聚焦波束分布测试结果如图 7所示。图中已对各波束电平值进行了归一化处理。
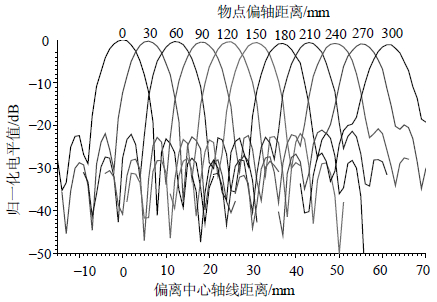 |
| 图7 像平面上聚焦波束电平分布测试结果(${S_o}$=3 500 mm, ${S_i}$=682 mm) |
测试结果表明,物平面上相距30 mm的两个物点,在像平面上形成聚焦波束中心间距为约6.1 mm,与理论值非常吻合;3 dB波束尺寸为约6.4 mm,比理论值偏大0.3 mm;随着物点偏轴距离的增大,像方波束电平值下降,偏轴300 mm时(最外侧波束),波束电平比中心波束降低约0.9 dB。因此,在设计馈源阵时,馈源中心间距应为6.1 mm。
将发射端天线置于像平面,并使其在像平面内以6 mm间隔依次横向偏移,然后让接收天线在物平面内横向移动,即测得物平面上聚焦波束信号电平分布,如图 8所示,图中也对各波束电平值进行了归一化处理。
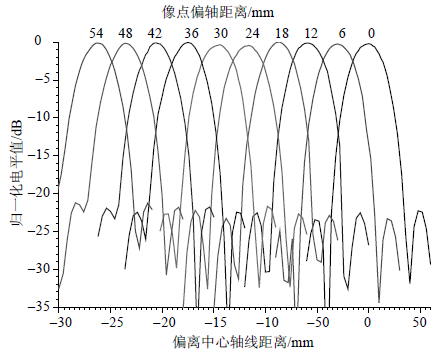 |
| 图8 物平面上聚焦波束电平分布测试结果(${S_o}$>=3 500 mm, ${S_i}$=682 mm) |
测试表明:在像平面上间隔6 mm的馈源,在物平面上形成的聚焦波束中心间距29 mm。由图像放大率关系可推知,若馈源间距为6.1 mm时,则物平面上聚焦波束中心间距将为约30 mm,与图 7测试结果相吻合。物平面上聚焦波束3 dB焦斑尺寸为约29.5 mm,比仿真结果展宽3.5 mm,但满足预期指标。
测试时只测试了透镜的单侧线性偏轴特性,由于透镜为轴对称结构,其另一侧偏轴特性也是相似的。根据测试结果可知,若将24个矩形喇叭馈源排成一列置于透镜像方焦平面上,并保持馈源间距$d$=6.1 mm,即可在距透镜3 500 mm的像平面上获得720 mm水平视场覆盖范围,在最佳聚焦位置处3 dB焦斑尺寸小于30 mm。
5 结束语准光介质透镜天线是近程被动毫米波成像系统的关键部件。本文针对3 mm波段焦平面阵列被动成像系统应用,设计了工作于3 mm波频段的大口径近程聚焦准光介质透镜天线。首先基于高斯准光理论设计了光路参数,然后利用ZEMAX强大的光学系统分析与综合能力,综合得到了具有小像差特性的非球面双凸透镜天线,再利用场仿真软件FEKO对设计结果进行验证。该设计方法简化了透镜天线轮廓的寻优设计过程,提高了透镜天线设计效率,并实现了对透镜天线波束束腰位置的精确设计。近场仿真结果表明,透镜天线的物距、像距将比ZEMAX中的设计值更小,因此在利用ZEMAX优化设计透镜轮廓时,采用的物距、像距应比设计值大才能获得所需的物距、像距。实测表明,所设计的介质透镜天线指标参数与设计参数吻合良好,且具有良好的波束均匀性,适用于近程被动毫米波焦平面阵列成像系统。
| [1] | YUJIRI L, SHOUCRI M, MOFFA P. Passive millimeter wave imaging[J]. IEEE Microwave Magazine, 2003, 4(3): 39-50. |
| [2] | PATI P, MATHER P. Open area concealed weapon detection system[C]//Proceeding of SPIE 8017, Detection and Sensing of Mines, Explosive Objects, and Obscured Targets XVI. Orlando: [s.n.], 2011. |
| [3] | STANKO S, NOTEL D, WAHLEN A, et al. Active and passive mm-wave imaging for concealed weapon detection and surveillance[C]//The 33rd International Conference on Infrared, Millimeter and Terahertz Waves. Pasadena: [s.n.], 2008. |
| [4] | SHI Xiang, YANG M H. Development of passive millimeter wave imaging for concealed weapon detection indoors[J]. Microwave and Optical Technology Letters, 2014, 56(7): 1701-1706. |
| [5] | VOLKOV P V, BELOV Y I, GORYUNOV A V, et al. Aspherical single-lens objective for radio-vision systems of the millimeter-wavelength range[J]. Technical Physics, 2014, 59(4): 588-593. |
| [6] | GOLDSMITH P F, HSIEH C T, HUGUENIN G R, et al. Focal plane imaging systems for millimeter wavelengths[J]. IEEE Transactions on Microwave Theory and Techniques, 1993, 41(10): 1664-1675. |
| [7] | SATO S, SAWAYA K, MIZUNO K, et al. Passive millimeter-wave imaging for security and safety applications[C]//Proceedings of SPIE 7671, Terahertz Physics, Devices, and Systems. Bellingham: [s.n.], 2010. |
| [8] | THAKUR J P, KIM W G, KIM Y H. Large aperture low aberration aspheric dielectronic lens antenna for w-band quasi optics[J]. Progress in Electromagnetics Research, PIER, 2010, 103: 57-65. |
| [9] | KIM W G, MOON N W, SINGH M K, et al. Characteristic analysis of aspheric quasi optical lens antenna in millimeter-wave radiometer imaging system[J]. Applied Optics, 2013, 52(6): 1122-1131. |
| [10] | QIU Jing-hui, ZHUANG Zhong, HAN Xue, et al. Design of quasi-optical subsystem for millimeter-wave imaging system[C]//The 8th International Symposium on Antennas Propagation & Em Theory. Kunming: IEEE Conference Publications, 2008: 530-533. |
| [11] | GOLDSMITH P F. Quasi-optical techniques[J]. Proceedings of the IEEE, 1992, 80(11): 1729-1747. |
| [12] | 窦文斌. 毫米波准光理论与技术[M]. 第2版. 北京: 高等教育出版社, 2006. DOU Wen-bin. Millimeter wave quasioptical theory and techniques (second edition)[M]. 2nd ed. Beijing: Higher Education Press, 2006. |
| [13] | GOLDSMITH P F. Quasi optical systems : Gaussian beam quasi optical propagation and applications[M]. New York: IEEE Press/chapman & Hall Publishers, 1998. |
 2016, Vol. 45
2016, Vol. 45
