人们对通信系统的要求是永无止境的,例如希望通信系统更廉价、更快速、更可靠、不但需要传输话音,还需要传输数据图像等,这些迫使许多研究者寻找取得接近或最终达到香农限的可靠通信的方式。文献[1]提出低密度奇偶校验(low density parity check,LDPC)码,近十几年来,它在纠错编码领域得到了极大的发展,已经成为了Turbo码的有力竞争者。LDPC码是最有希望在广泛的信道范围下接近香农极限的误差纠正技术[2]。
根据LDPC码校验矩阵的构造方式的不同,编码的构造方法主要分为随机构造和结构化构造两类。随机构造的方法虽然纠错性能优秀,但是由于校验矩阵的随机性无法实现简单编码,编码复杂度高、硬件成本昂贵且不易于实现[3, 4]。结构型码由于其校验矩阵的准循环特性使其备受青睐,具有代表性的结构型码主要是文献[5, 6]提出的一系列基于有限几何和基于有限域的LDPC码的构造方法。由于LDPC码不允许存在短环,否则将使得译码器不能快速收敛甚至不能收敛,因此构造大围长的LDPC码成为编码学的研究热点[7]。文献[8]提出了一类QC-LDPC码存在2k环的充要条件,码字性能非常优秀,但缺点是循环置换矩阵的维数P值下界不能简单连续取值。文献[9]提出当列重为5、6及不小于7的3种情况时,依次利用完全确定的方式构造围长为8的QC-LDPC码。文献[10]基于环约束方程并利用贪婪算法获得大围长的OCS-LDPC码,需要通过计算机搜索获得。文献[11]的确定码和文献[12]的QF-LDPC码都是定式构造围长为8的码字,但是由于列重为3的单一选择以及码率受限,导致实际应用有很大的局限性。
本文利用卢卡斯数列(Lucas sequence)的性质提出了一种行重为k,列重为j(j≥3)的规则的卢卡斯QC-LDPC(L-QC-LDPC)码构造方法。这种方法构造出来的QC-LDPC码可以有效地避免短环,且L-QC-LDPC的围长至少为8;特别地,该方法构造码的码型都具有一定的结构特征、计算复杂度低、易于硬件实现且p值的下界允许连续取值。
1 QC-LDPC码的通用构造方法QC-LDPC码的校验矩阵是由分组矩阵构成的,而每个分组的矩阵又是由满秩的循环置换矩阵和全0的方阵组合而成。校验矩阵H的列重和行重分别用j和k表示,QC-LDPC码的校验矩阵为:
| $H = {\left[{\begin{array}{*{20}{c}} {{I_{y(0,0)}}}&{{I_{y(0,1)}}}&{{I_{y(0,2)}}}& \cdots &{{I_{y(0,k - 1)}}}\\ {{I_{y(1,0)}}}&{{I_{y(1,1)}}}&{{I_{y(1,2)}}}& \cdots &{{I_{y(1,k - 1)}}}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {{I_{y(j - 1,0)}}}&{{I_{y(j - 1,1)}}}&{{I_{y(j - 1,2)}}}& \cdots &{{I_{y(j - 1,k - 1)}}} \end{array}} \right]_{pj \times pk}}$ | (1) |
对应的指数矩阵为:
| $W = {\left[{\begin{array}{*{20}{c}} {y(0,0)}&{y(0,1)}&{y(0,2)}& \cdots &{y(0,k - 1)}\\ {y(1,0)}&{y(1,1)}&{y(1,2)}& \cdots &{y(1,k - 1)}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {y(j - 1,0)}&{y(j - 1,1)}&{y(j - 1,2)}& \cdots &{y(j - 1,k - 1)} \end{array}} \right]_{j \times k}}$ | (2) |
式中,2≤j≤k≤p;I0是p×p维的单位矩阵;In是置换矩阵,通过I0右移n位得到;指数矩阵中的y(s,i)(0≤s<j,0≤i<k)表示该循环置换矩阵的移位值。
校验矩阵含有的环可以用对应的指数矩阵中的元素表示,QC-LDPC码中长度为2k的环可以表示为y(s0,i0),y(s0,i1),y(s1,i1),…,y(sk-1,ik-1),y(sk-1,i0),y(s0,i0)。文献[8]给出了校验矩阵中存在长度为2k的环的充要条件满足式(3),其中,it≠it+1,st≠st+1。构造LDPC码的首要条件就是避免四环,即y(s0,i0)-y(s1,i0)+y(s1,i1)-y(s0,i1)≠0 mod p。因此若要使得设计的QC-LDPC码避免存在长度为2k的环,就必须通过一定规则的设计使得下式不成立:
| $\begin{array}{*{20}{c}} {\sum\limits_{t = 0}^{k - 1} {(y({s_t},{i_t}) - y({s_{t + 1}},{i_t}))} = 0}&{\bmod p} \end{array}$ | (3) |
定义1 对于一个整数数列l(n),n为正整数。如果l(n)=l(n-1)+l(n-2),n≥3且l(1)=2,l(2)=1,满足以上初始条件和递推关系的数列称为卢卡斯数列,它的每一项称为卢卡斯数。
典型卢卡斯数列表示如下:2,1,3,4,7,11,18,39,57,96,…。
定理1 对于一个卢卡斯数列,若n>m且n,m,k∈Z+,则有l(n+k)-l(n)>l(m+k)-l(m)[13]。
本文基于卢卡斯数列中元素的性质特征构造出一个列重和行重分别为j和k、围长至少为8的规则QC-LDPC码。
2.2 基于卢卡斯数列的QC-LDPC码的构造方法首先构造一个指数矩阵为:
| $W = {\left[{\begin{array}{*{20}{c}} 0&0& \cdots &0\\ {l(0)}&{l(1)}& \cdots &{l(k - 1)}\\ {l(j + 1)}&{l(j + 2)}& \cdots &{l(j + k)}\\ {l(2(j + 1))}&{l(2(j + 1) + 1)}& \cdots &{l(2(j + 1) + k - 1)}\\ \vdots & \vdots & \ddots & \vdots \\ {l((j - 2)(j + 1))}&{l((j - 2)(j + 1) + 1)}& \cdots &{l((j - 2)(j + 1) + k - 1)} \end{array}} \right]_{j \times k}}$ | (4) |
式中,W的维数为j×k,j≥3,k>j。指数矩阵W的第一行为全0,第二行为集合{l(n)}中的前k个元素:l(0),l(1),…,l(k-1);从集合{l(n)}中的第j+1个元素开始到第j+k个元素作为指数矩阵的第三行:l(j+1),l(j+2),…,l(j+k);…;最后一行的元素为:l((j-2)(j+1)),l((j-2)(j+1)+1),…,l((j-2)(j+1)+k-1),即指数矩阵中任意元素y(s,i)( 0≤s<j,0≤i<k),当s=0时,y(s,i)=0;当s≠0时,y(s,i)=l((s-1)(j+1)+i)。然后对指数矩阵W进行填充,W中对应的元素用p×p的单位矩阵及其相应的循环移位矩阵替换,其中p>l((j-2)(j+1)+k-1);0元素用p×p的单位矩阵I0替换,Iy(s,i)用相应的单位矩阵右循环移位y(s,i)位得到的矩阵I(l((s-1)(j+1)+i))进行替换,最终构成校验矩阵H。
定理2 只要满足p>l((j-2)(j+1)+k-1),基于卢卡斯数列构造的QC-LDPC码的校验矩阵H对应的Tanner图的围长至少为8。
证明:为了证明H对应的Tanner图中的环长为8,要依次证明Tanner图中没有四环和六环。
对于四环,由式(3)可知要避免四环即y(s0,i0)-y(s1,i0)+y(s1,i1)-y(s0,i1) ≠0 mod p。为了不失去一般性,假设i0<i1,s0<s1,则有:
y(s0,i1)-y(s0,i0)=l((s0-1)(j+1)+i1) -
l((s0-1)(j+1)+i0)
y(s1,i1)-y(s1,i0)=l((s1-1)(j+1)+i1)-
l((s1-1)(j+1)+i0)
由定理1可得:
y(s1,i1)-y(s1,i0)>y(s0,i1)-y(s0,i0),
0<y(s1,i1)-y(s1,i0)+y(s0,i0)-y(s0,i1)<p
因此所构造的校验矩阵已经有效地避免了四环的存在。
对于六环,Tanner图中存在六环的可能性有6种形式,如图 1所示。
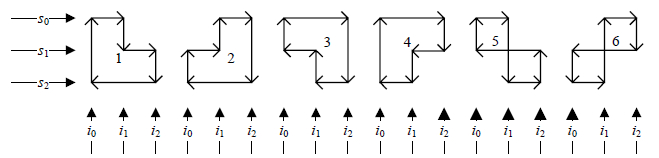 |
| 图1 6种六环的存在形式 |
图 1所示6种六环的存在形式,根据结构形式可将其分为两类:前4种具有相同的结构形式为一类,后两种具有相同的结构形式为另一类。每一类中的任意形式可以在已知其中一种的情况下,通过特定的方式得到其他形式。所以,为了证明H矩阵中不存在六环,只需分别证明这两种结构任意一种形式是不存在的,理论分析及证明如下:
1) 第一大类
图 1中的形式1的六环不存在性证明分为两种情况。
① 当六环的所在位置的第一行就是校验矩阵的第一行,即s0=0,令ti=si-1,1≤i<j,由式(3)和式(4)可得:
y(s0,i0)-y(s0,i1)+y(s1,i1)-
y(s1,i2)+y(s2,i2)-y(s2,i0)=
0-0+l(t1(j+1)+i1)-l(t1(j+1)+i2)+
l(t2(j+1)+i2)-l(t2(j+1)+i0)=
l(t1(j+1)+i1)-l(t1(j+1)+i2)+
l(t2(j+1)+i2)-l(t2(j+1)+i0)
由图 1中的第一种形式令i0=i2-m,i1=i2-n且m>n,原式可以简化为:
| $\begin{array}{l} l\left( {{t_1}\left( {j + 1} \right) + {i_2} - n} \right) - l\left( {{t_1}\left( {j + 1} \right) + {i_2}} \right) + \\ l\left( {{t_2}\left( {j + 1} \right) + {i_2}} \right) - l\left( {{t_2}\left( {j + 1} \right) + {i_2} - m} \right) = \\ \left\{ {l\left( {{t_2}\left( {j + 1} \right) + {i_2}} \right) - l\left( {{t_2}\left( {j + 1} \right) + {i_2} - m} \right)} \right\} - \\ \;\left\{ {l\left( {{t_1}\left( {j + 1} \right) + {i_2}} \right) - l\left( {{t_1}\left( {j + 1} \right) + {i_2} - n} \right)} \right\} \end{array}$ | (5) |
由定理1可得:l(t2(j+1)+i2)-l(t2(j+1)+i2-m)>l(t1× (j+1)+i2)-l(t1(j+1)+i2-n)。
所以,0<(5)<l(t2(j+1)+i2)<p,即原式≠0 mod p。
② 当s0≠0时,有:
y(s0,i0)-y(s0,i1)+y(s1,i1)-
y(s1,i2)+y(s2,i2)-y(s2,i0) >
y(s0,i0)-y(s0,i1)+y(s1,i1)-
y(s1,i2)+y(s1,i2)-y(s1,i0) =
y(s0,i0)-y(s0,i1)+y(s1,i1)-
y(s1,i0)>0
y(s0,i0)-y(s0,i1)+y(s1,i1)-
y(s1,i2)+y(s2,i2)-y(s2,i0) <
y(s2,i0)-y(s0,i1)+y(s1,i1)-
y(s1,i2)+y(s2,i2)-y(s2,i0) =
y(s1,i1)-y(s0,i1)+y(s2,i2)-
y(s1,i2)<y(s1,i2)+y(s2,i2)-
y(s1,i2)=y(s2,i2)<p
所以利用夹逼准则可知,原式≠0 mod p。
2) 第二大类
图 1中的形式5的六环不存在性证明也分为两种情况。
① 六环的所在位置的第一行就是校验矩阵的第一行,即s0=0,令ti=si-1,1≤i<j,由式(3)和式(4)可得:
y(s0,i0)-y(s0,i1)+y(s2,i1)-
y(s2,i2)+y(s1,i2)-y(s1,i0)=
0-0+l(t2(j+1)+i1)-l(t2(j+1)+i2)+
l(t1(j+1)+i2)-l(t1(j+1)+i0)=
l(t2(j+1)+i1)-l(t2(j+1)+i2)+
l(t1(j+1)+i2)-l(t1(j+1)+i0)
由图中的第五种形式令i0=i2-m,i1=i2-n且m>n,原式可以简化为:
| $\begin{array}{l} l\left( {{t_2}\left( {j + 1} \right) + {i_2} - n} \right) - l\left( {{t_2}\left( {j + 1} \right) + {i_2}} \right) + \\ l\left( {{t_1}\left( {j + 1} \right) + {i_2}} \right) - l\left( {{t_1}\left( {j + 1} \right) + {i_2} - m} \right) = \\ \left\{ {l\left( {{t_1}\left( {j + 1} \right) + {i_2}} \right) - l\left( {{t_1}\left( {j + 1} \right) + {i_2} - m} \right)} \right\} - \\ \;\left\{ {l\left( {{t_2}\left( {j + 1} \right) + {i_2}} \right) - l\left( {{t_2}\left( {j + 1} \right) + {i_2} - n} \right)} \right\} \end{array}$ | (6) |
由定理1可得:
l(t1(j+1)+i2)-l(t1(j+1)+i2-m)<
l(t2(j+1)+i2)-l(t2(j+1)+i2-n)
所以,0>(6)>-l(t2(j+1)+i2),即原式≠0 mod p。
② 当s0≠0时,有:
y(s0,i0)-y(s0,i1)+y(s2,i1)-
y(s2,i2)+y(s1,i2)-y(s1,i0)<
y(s1,i0)-y(s1,i1)+y(s2,i1)-
y(s2,i2)+y(s1,i2)-y(s1,i0)=
y(s1,i2)-y(s1,i1)+y(s2,i1)-y(s2,i2)<0
y(s0,i0)-y(s0,i1)+y(s2,i1)-
y(s2,i2)+y(s1,i2)-y(s1,i0)>
y(s0,i0)-y(s0,i1)+y(s2,i1)-
y(s2,i2)+y(s0,i2)-y(s0,i0)=
y(s0,i2)-y(s0,i1)+y(s2,i1)-
y(s2,i2)>y(s2,i1)-y(s2,i2)>
-y(s2,i2)>-p
所以,利用夹逼准则可知,原式≠0 mod p。
综上所述,图 1中的6种六环形式是不存在的。因此当p>l((j-2)(j+1)+k-1)时,构造的L-QC-LDPC码的校验矩阵对应的Tanner图中没有四六环,定理2得证。
通常情况下,QC-LDPC码为了存储其校验矩阵,需要存储指数矩阵中的每一个元素值,即使是仅仅存储每一个元素值,也需要一定的存储空间,对于编码器来说,节省存储空间就是降低实际应用中的成本。而对于卢卡斯数列,仅需存储0、l(1)和l(2)的3个元素,其他元素的值可由简单的加法和乘法运算得到,这样很大程度上节省了系统所需要的存储空间。
3 性能分析本文在仿真中采用BPSK调制,传输信道选用AWGN信道,采用BP译码算法。首先基于卢卡斯数列所构造的L-QC-LDPC码指数矩阵如式(4)所示;然后确定所构造的LDPC码的列重和行重的参数j和k,构造一个j×k的指数矩阵;例如j=3,k=6,对应的指数矩阵W可以表示为W(3,6)。将k维的全0向量作为指数矩阵的第一行,前k个卢卡斯数作为指数矩阵的第二行,第四个到第k+3个数作为指数矩阵的第三行,即得到指数矩阵:
| ${\bf{W}}{\rm{(3,6) = }}\left[{\begin{array}{*{20}{c}} 0&0&0&0&0&0\\ 2&1&3&4&7&{11}\\ 4&7&{11}&{18}&{29}&{47} \end{array}} \right]$ | (7) |
通过指数矩阵确定参数p,上述指数矩阵p的取值范围为p>47,为构造码长1302的QC-LDPC码,令p=217,指数矩阵中的0元素扩展为217×217的单位矩阵I0,其他元素扩展为相应的单位矩阵的右循环移位。图 2给出了所构造的码字在BP译码中不同迭代次数下的误码性能,由图 2可见,在BER为10-5时,迭代次数为10、20、30、40和50时所需的SNR分别为:3.81、3.60、3.48、3.45和3.43dB,距香农限分别为:3.623、3.413、3.293、3.263和3.243dB。在SNR=4.0dB的情况下,所对应的BER分别约为:3.277×10-6、7.424×10-7、3.84×10-7、3.064×10-7和2.569×10-7。通过以上分析可以得出,随着迭代次数的增加,纠错性能越来越好,但NCG提高幅度却越来越小。迭代过程其实是节点信息更新的一个过程,变量节点译码器将附加的信息传送给校验节点译码器,然后校验节点译码器将更新的信息传送给变量节点译码器,如此迭代,最终完成整个译码过程。但是当每个译码器信息更新到一定量后,每次迭代后再转化的信息很少,对结果影响不大,甚至有可能没有需要再转化的信息。通过仿真分析可以看出,译码迭代30次与50次时与香农限仅仅相差0.05dB左右,非常接近,而译码迭代50次时时间复杂度和运算量都较高。因此,需要在复杂度和纠错性能之间找到一个折衷点,所以选择迭代30次。
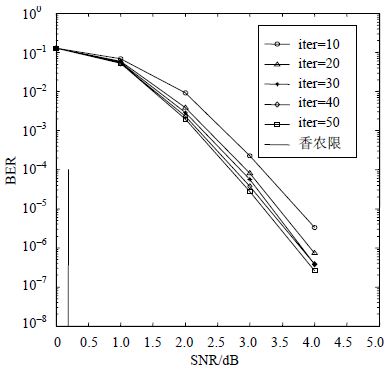 |
| 图2 不同迭代次数的误码性能图 |
为充分说明(1302,651)L-QC-LDPC码的纠错性能,在相同条件下不同码字仿真结果如图 3所示。由图 3可知,在误码率为10-6时,在相同的码长、1/2码率的条件下,所构造的L-QC-LDPC码与其他算法构造的码相比,均有不同程度的性能提升,如表 1所示。从表中可以看出,L-QC-LDPC码与文献[10]的OCS-LDPC码相比,可获得约2dB的净编码增益,与文献[11]的确定性码及文献[12]的QF-LDPC码相比,分别有约0.8dB和0.1dB净编码增益的改善。在相近码长、相同行列重和码率的情况下,所提出的码字与文献[7]中基于有限域的循环子集的QC- LDPC码相比,提高了约0.5dB的净编码增益的改善。同时可以从表中看出,本文提出的码最接近香农限。
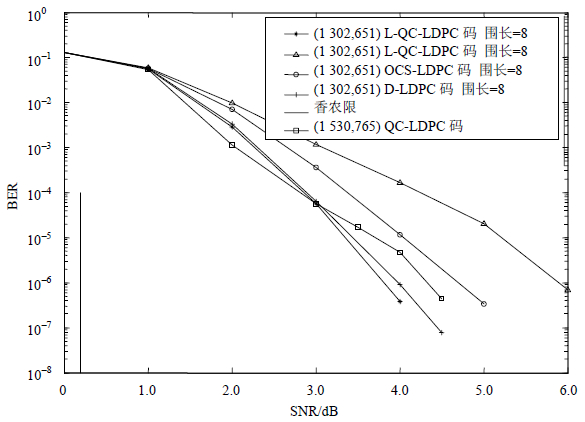 |
| 图3 不同码字的性能对比图 |
| 表1 不同对比算法所构造的码与香农限的距离及和L-QC-LDPC码相比获得的净编码增益 |
本文提出一种基于卢卡斯数列构造围长至少为8的规则L-QC-LDPC码的确定性方法。当p>l((j-2)(j+1)+k-1)时,这类码字可以有效地避免四六环。仿真结果表明,在同等条件下,L-QC-LDPC码的性能明显优于OCS-LDPC码和确定性码,略优于QF-LDPC码。与OCS-LDPC码相比,其构造简单,不需要借助计算机搜索或者计算,虽然确定性码和QF-LDPC码都是定式构造—给定校验矩阵的显式表达式,但是它们的列重受限。除此之外,对于编码器而言,基于卢卡斯数列的码字只需要存储3个元素:0、l(1)和l(2),其他元素的值可以通过简单的加法和乘法运算得到,可以有效地节约系统所需要的存储空间,进而降低硬件实现成本和复杂度。
| [1] | GALLAGER R. Low-density parity-check codes[J]. IRE Transactions on Information Theory, 1962, 8(1): 21-28. |
| [2] | MACKAY D J C, NEAL R M. Near Shannon limit performance of low density parity check codes[J]. Electronics letters, 1996, 32(18): 1645. |
| [3] | MACKAY D J C. Good error-correcting codes based on very sparse matrices[J]. IEEE Transactions on Information Theory, 1999, 45(2): 399-431. |
| [4] | ASVADI R, BANIHASHEMI A H. A rate-compatible puncturing scheme for finite-length LDPC codes[J]. IEEE Communications Letters, 2013, 17(1): 147-150. |
| [5] | TANG H, XU J, LIN S, et al. Codes on finite geometries[J]. IEEE Transactions on Information Theory, 2005, 51(2): 572-596. |
| [6] | HAN G, GUAN Y, KONG L. Construction of irregular QC-LDPC codes via masking with ACE optimization[J]. IEEE Communications Letters, 2014, 18(2): 348-351. |
| [7] | ZHANG L, LIN S, ABDEL-GHAFFAR K, et al. Quasi-cyclic LDPC codes on cyclic subgroups of finite fields[J]. IEEE Transactions on Communications, 2011, 59(9): 2330-2336. |
| [8] | FOSSORIER M P C. Quasicyclic low-density parity-check codes from circulant permutation matrices[J]. IEEE Transactions on Information Theory, 2004, 50(8): 1788-1793. |
| [9] | ZHANG J, ZHANG G. Deterministic girth-eight QC-LDPC codes with large column weight[J]. IEEE Communications Letters, 2014,18(4): 656-659. |
| [10] | HUANG J F, HUANG C M, YANG C C. Construction of one-coincidence sequence quasi-cyclic LDPC codes of large girth[J]. IEEE Transactions on Information Theory, 2012, 58(3): 1825-1836. |
| [11] | 张国华, 陈超, 杨洋, 等. Girth-8 (3,L)-规则 QC-LDPC 码的一种确定性构造方法[J]. 电子与信息学报, 2010, 32(5): 1152-1156. ZHANG Guo-hua, CHEN Chao, YANG Yang, et al. Girth-8 (3,L)-regular QC-LDPC codes based on novel deterministic design technique[J]. Journal of Electronics & Information Technology, 2010, 32(5): 1152-1156. |
| [12] | ZHANG G, SUN R, WANG X. Deterministic construction of girth-eight (3,L) QC-LDPC codes from quadratic function[J]. Electronics Letters, 2013, 49(9): 600-602. |
| [13] | FU Cheng-hua, LI Xiu-li. Construction of QC-LDPC codes on combinatorial sequences[C]//]2013 Fifth International Conference on Intelligent Human-Machine Systems and Cybernetics. [S.l.: IEEE, 2013(2): 74-78. |
 2016, Vol. 45
2016, Vol. 45
