一个能充分反映接收信号衰落统计特性的陆地移动卫星(LMS)信道模型是卫星通信和广播系统设计的关键。近年来对LMS信道模型的研究主要集中在不同频段、不同场景和不同仰角下统计特性及传播参数的估计。文献[1]给出了Loo、Corazza和Suzuki等统计模型,均假定在给定仰角和场景下时间序列服从唯一的分布。文献[2]在Markov链的基础上研究了能描述窄带和宽带信号动态行为的LMS信道统计模型,给定环境和仰角下信号变化的参数是固定的。文献[3]针对多卫星LMS信道模型估计了传播参数之间的相关性。文献[4]研究了两状态窄带LMS信道模型及双卫星信道分集的四状态模型,并基于抽头延迟线概述了宽带LMS信道模型。以上提出的信道模型能用于模拟真实的传播环境,但信号变化的单一分布或固定不变的传播参数在一定程度上影响了LMS系统参数的选择。
本文提出改进的两状态LMS信道模型,适合DVB-SH[5, 6]系统。该模型在三状态LMS信道模型[7, 8, 9, 10]的基础上采用“好”、“坏”状态代表阴影衰落,并由一阶离散Markov链[10]或semi_Markov链[11, 12]控制状态之间的转移,在新状态到达时刻根据传播参数之间的联合分布获取当前状态的参数。同时,在能真实反映LMS信道传播特性的前提下对接收信号进行功率控制(PC)[13],对缓慢突发阴影迅速做出反应,缩小信道衰落因子的动态范围,降低卫星发射功率、增加DVB-SH系统的多媒体业务的可靠性。该模型具有复杂度低、拟合性好及通用性等特点。
1 三状态LMS信道模型DVB-SH系统是一个卫星与陆地的混合系统,结合卫星接收和陆地转发在城市、城郊和乡村等覆盖区之间提供高质量移动电视广播业务。在DVB-SH系统中,由物理层交织器深度和LL-FEC引入的时间分集能确保卫星链路的有效性,因此非视距状态成为估计卫星空中接口性能的关键。
将信道的非常慢衰落成分模型化为信道状态,根据当前状态和接收环境生成视距信号和非视距信号的幅度,并采用对数正态模型、莱斯模型和瑞利模型的不同结合描述窄带LMS传播信道的衰落,以此得到复包络的时间序列。三状态LMS信道模型采用“视距”、“阴影”和“阻塞”划分阴影遮蔽情况,状态间转移由一阶离散Markov链控制,并假设每一状态内接收信号的包络服从固定模型参数的Loo分布,是DVB-SH标准分析的基础。包络的概率密度函数可表示为:
| $\begin{array}{l} f(r) = \int_{{\rm{ }}0}^{{\rm{ }}\infty } {f(r|z)} f(z){\rm{d}}z,r \ge 0{\rm{ = }}\\ \frac{{8.686r}}{{{\sigma ^2}{\sum _A}\sqrt {2{\rm{\pi }}} }}\int_{\,0}^{\,\infty } {\frac{1}{z}} \exp \left[{ - \frac{{{r^2} + {z^2}}}{{2{\sigma ^2}}}} \right] \times \\ \exp \left[{ - \frac{{{{(20\log z - {M_A})}^2}}}{{2\sum _{\rm A}^2}}} \right]{I_0}\left( {\frac{{rz}}{{{\sigma ^2}}}} \right){\rm{d}}z \end{array}$ | (1) |
式中,$z$是直射信号的幅度;$\sigma = \sqrt {{{10}^{{\rm{MP/10}}}}/2} $是多径分量的功率;${M_A}$、${\sum _A}$分别表示对数正态分布的均值和标准偏差。模型参数${\rm{Loo}}({M_A},{\sum _A},{\rm{MP}})$在给定场景和仰角下是固定不变的,以dB为单位,因此在每一状态内Loo分布是唯一的。
2 改进的两状态LMS信道模型随着未来移动广播系统对衰减裕量的需求,非视距条件需要更好的统计特性,而三状态LMS信道模型存在的缺陷影响了DVB-SH系统标准的分析且不满足卫星到移动终端视距链路裕量的要求,因此本文提出改进的两状态LMS信道模型,其框图如图 1所示。
 |
| 图1 改进的两状态LMS信道模型实现框图 |
SSG模块描述了两个状态:“好”状态代表视距到轻阴影范围内的衰落,“坏”状态代表重阴影到阻塞范围内的衰落。在一帧内由Markov链或semi- Markov链更新信道状态,其状态模型如图 2所示。
 |
| 图2 两状态的状态模型 |
Markov链由转移概率矩阵$P$获得精确的状态概率矩阵$W$和平均状态持续时间,它的状态持续时间概率密度服从指数分布,在LMS信道中,这是不精确的。对于semi-Markov链,每一状态的持续时间概率密度服从对数正态分布[12],分别采用${\mu _{{\rm{Dur}}}}$、${\sigma _{{\rm{Dur}}}}$代表状态持续时间的均值和标准偏差。相比Markov模型,它采用当前状态和平均状态持续时间改善了状态持续时间的统计特性,对系统同步、系统有效性估计及中断周期至关重要。SSG模块的输出为当前状态和状态持续时间${D_{{\rm{state}}}}$。
2.2 传播参数生成器(PPG)在PPG中,新状态的模型参数与SSG输出的当前状态及终端的接收环境有关,其联合的统计分布为:
| $\left\{ \begin{array}{l} f({M_A}) \sim {\rm N}({\mu _1},{\sigma _1})\\ f({\sum _A}|{M_A}) \sim {\rm N}({\mu _2},{\sigma _2})\\ f({\rm{MP}}) \sim {\rm N}({\mu _3},{\sigma _3}) \end{array} \right.$ | (2) |
式中,
| $\left\{ \begin{array}{l} {\mu _2} = {a_1}M_A^2 + {a_2}{M_A} + {a_3}\\ {\sigma _2} = {b_1}M_A^2 + {b_2}{M_A} + {b_3} \end{array} \right.$ | (3) |
相比三状态LMS信道模型,该模型的传播参数能在接收信号的动态范围上获得可靠的模型,具有大范围的参数空间。
2.3 Loo生成器Loo生成器根据当前状态及PPG输出的传播参数生成多径快衰落和视距慢衰落。其中,快衰落采用巴特沃斯低通滤波器引入由移动终端运动引起的多普勒扩展,传递函数可以表示为:
| ${\left| {H(f)} \right|^2} = B/[1 + {(f/{f_c})^{2k}}]$ | (4) |
式中,${f_c}$为3 dB截止频率;$k$为滤波器的阶数。为了确保复高斯过程的标准偏差经过滤波器后不变,采用$B$将滤波器的能量归一化为1。在慢衰落信号中引入相位的变化,它与移动终端速度$v$、相对卫星的运动方向$\varphi $和卫星仰角$\theta $有关。初始相位为:
| $\Delta {\phi _1} = 2{\rm{\pi }}\frac{v}{c}f\cos (\varphi )\cos (\theta ){T_s}$ | (5) |
式中,$f、c$是载波频率和光速;${T_s}$是采样间隔。视距信号的相位$\Delta {\varphi _1}[n]$是初始相位的时间序列。对受阴影影响的视距信号以相关距离${l_{{\rm{corr}}}}$进行采样,并以不低于8倍最大多普勒频移的采样率得到快衰落信号。在生成复时间序列时,可通过样条插值法对慢衰落信号进行采样率的转换。在Loo生成器中,与文献[6]不同的是:先进行采样率转化和插值,再转化为对数正态分布,确保了慢衰落的对数正态阴影。同时,需要对接收到的复时间序列相对于LoS电平归一化处理,以消除视距传播的损失。
2.4 PC机制由于两状态LMS信道模型生成复时间序列的动态范围较大,在能真实反映信道传播特性的前提下,对接收信号包络进行PC,以跟踪、纠正快衰落和补偿慢衰落,从而缩小信号的动态范围,同时以最小发射功率保证准确的通信链路性能和降低同频干扰。忽略传播时延和卫星与移动终端的处理时间,在1s内,反馈链路向卫星发送1 500次控制命令:增加或减少1 dB发射功率。为了优化接收信号的PC过程,采用预处理滤波器推测接收信号,其控制门限为每一帧长内接收信号功率的中值。控制过程为:
1) 在一帧内生成复时间序列,计算控制门限。
2) 根据滑动窗的持续时间,计算窗内接收信号包络功率的平均值,若大于控制门限,控制信号减
1 dB;反之,加1 dB,更新下一个窗内的接收信号的功率,记录此帧内控制后的接收信号序列。
3) 判断是否为最后一帧,若不是返回过程2),反之,PC机制结束。
该模型可以用于L频段和S频段,且移动终端与卫星之间的仰角为40°、60°、80°时的城市、城郊、开阔地、树阴影等场景。为了验证该模型的准确性和通用性,可以选择不同的传播场景,将其一阶、二阶统计特性与实测数据比较,同时,针对树阴影坏境研究PC机制信号的统计特性。
3 仿真分析图 3给出了改进模型的仿真流程,它包含SSG、PPG、Loo生成器和PC机制,可实现两状态LMS信道模型衰落统计特性的分析及控制前后信号统计特性的统计归一化均方误差。
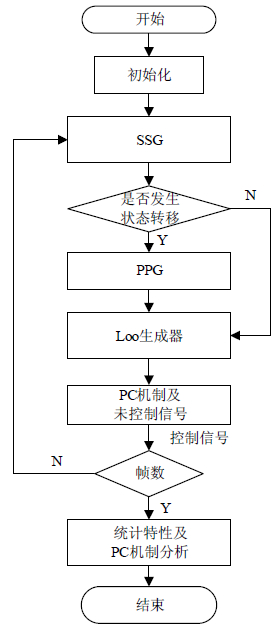 |
| 图3 模型的仿真流程图 |
基于图 1所示的模型对本文提出的改进LMS信道模型的衰落统计特性进行研究,仿真参数设置如下。在DVB-SH系统中,考虑S频段,卫星仰角40°,快衰落采样间隔为1/8波长,慢衰落采用间隔为${l_{{\rm{corr}}}} = 2\;{\rm{m}}$,帧长5 m,巴特沃斯低通滤波器的通带、阻带归一化截止频率分别为0.225和0.75,进行500 000个采样。
3.1 两状态LMS信道统计分析选择城郊场景,移动终端速度50 km/h,将改进的两状态LMS信道模型的一阶、二阶衰落统计特性与三状态LMS信道模型、文献[6]及实测数据比较,验证所建信道模型的准确性,仿真结果如图 3所示。其中实测数据来源于:CNES在法国南部,频率2.1775 GHz和卫星仰角40°左右测得的数据及英国布拉德福德大学在S频段(2.618 GHz),卫星仰角40°、60°和80°下对开阔地、城郊、城市和树阴影环境实测的数据。
图 3表明尽管改进模型与文献[6]有一致的一阶统计特性,但归一化电平通过率与实测之间的偏差低于文献[6]。
图 3a表明两状态和三状态模型的一阶统计特性与实测数据拟合的很好,相比Markov模型,semi-Markov模型的接收信号动态范围更小。同时,经计算实测信号与仿真信号的残余累积分布函数之间的欧几里德距离大于10%,对于给定传播场景及仰角常选择距离最小的模型。
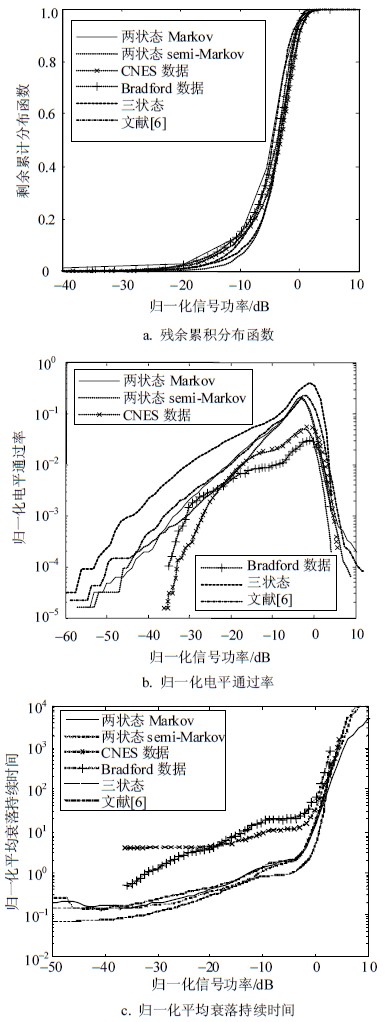 |
| 图 3 城郊环境40°仰角两状态Markov和semi-Markov模型的一阶、二阶衰落统计特性 |
图 3b和图 3c表明相比一阶统计特性,二阶统计特性与实测数据拟合稍差,这是由实测中幅度和相位的频率响应受不精确的多普勒频带宽度影响引起的。同时,改进的两状态比三状态模型变化趋势慢,与实测数据拟合的更好。
3.2 PC机制的仿真分析对于PC机制,假设滑动窗持续时间为$1/1\;500\;{\rm{s}}$,终端的速度范围为$50\;{\rm{km/h}} \le v \le 5\;000\;{\rm{km/h}}$,15次仿真后统计归一化均方误差。针对中级树阴影,图 4a和图 4b分别基于Markov模型和semi-Markov模型给出了控制前后时间序列的残余累积分布函数、归一化电平通过率的归一化均方误差的统计平均值。
 |
| 图4 中级树阴影S波段40°仰角下PC机制的归一化均方误差 |
图 4a和图 4b表明:PC机制下接收信号的一阶、二阶衰落统计特性与实测数据拟合的较好,仍能准确地表征LMS信道的传播特性。相比Markov模型,semi_Markov模型的PC机制跟踪、纠正快衰落和补偿慢衰落能力较强,在维持链路性能的前提下信号衰减较大,能在更大程度上降低发射信号功率和同频干扰。仿真结果还表明:移动终端速度在250 km/h时,能获得最大的控制增益和最小的动态范围;而随着速度的增加,在相同的仿真路径下,更新次数减少,跟踪和纠正能力降低,当达到3 650 km/h时,PC机制失效。因此PC机制能在一定的终端速度下获得最大的控制增益。
4 结论为了解决三状态LMS信道模型在给定场景和卫星仰角下每一状态传播参数固定不变且统计特性不能很好地拟合到实测数据的缺陷,本文提出了改进的两状态LMS信道模型。在准确反应传播特性的前提下,引入PC机制减少信号的衰减,适用于DVB-SH系统中不同场景、不同频段、不同卫星仰角和方位角下LMS信道的模拟,能为DVB-SH标准的参数选择提供准确的信息,并可扩展到单卫星接收的MiLADY模型[14]中。具有复杂度低、可靠性高及通用性等特点。
| [1] | FONTAN F P, MAYO A, MAROTE D, et al. Review of generative models for the narrowband land mobile satellite propagation channel[J]. International Journal of Satellite Communications and Networking, 2008, 26(4): 291-316. |
| [2] | FONTAN F P, CASTRO M V, CABADO C E, et al. Statistical modeling of the LMS channel[J]. IEEE Trans on Vehicular Technology, 2001, 50(6): 1549-1567. |
| [3] | KONIG J, ARNDT D, IHLOW A, et al. Estimation of fading parameter correlation for modeling the land mobile satellite channel[C]//IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). Seoul: IEEE, 2012: 1-5. |
| [4] | LUTZ E. Modelling of the satellite communications channel-With emphasis on the land mobile satellite channel[C]//IEEE First AESS European Conference on Satellite Telecommunications (ESTEL). Rome: IEEE, 2012: 1-7. |
| [5] | Digital Video Broadcasting (DVB). Framing structure, channel coding and modulation for satellite services to handheld devices(SH) below 3 GHz[S]. ETSI 302 583 V1.1.0 (2008-01). |
| [6] | CERDEIRA R P, FONTAN F P, BURZIGOTTI P, et al. Versatile two-state land mobile satellite channel model with first application to DVB-SH analysis[J]. International Journal of Satellite Communications and Networking, 2010, 28(5-6): 291-315. |
| [7] | FONTAN F P, CASTRO M A V, BUONOMO S, et al. S-band LMS propagation channel behaviour for different environments, degrees of shadowing and elevation angles[J]. IEEE Trans on Broadcasting, 1998, 44(1): 40-76. |
| [8] | BURZIGOTTI P, CERDEIRA R P, ALAMANAC A B, et al. DVB-SH analysis using a multi-state land mobile satellite channel model[C]//Advanced Satellite Mobile Systems, 2008, ASMS 2008 4th. Bologna: IEEE, 2008: 149-155. |
| [9] | FONTAN F P, LAGO I S, CERDEIRA R P, et al. Consolidation of a multi-state narrowband land mobile satellite channel model[C]//The Second European Conference on Antennas and Propagation(EuCAP). Edinburgh: IET, 2007: 1-6. |
| [10] | MILOJEVIC M, HAARDT M, EBERLEIN E, et al. Channel modeling for multiple satellite broadcasting systems[J]. IEEE Trans on Broadcasting, 2009, 55(4): 705-718. |
| [11] | BRATEN L E, TJELTA T. Semi-Markov multistate modeling of the land mobile propagation channel for geostationary satellites[J]. IEEE Trans on Antennas and Propagation, 2002, 50(12): 1795-1802. |
| [12] | REY I D, SANCHEZ M G. Semi-Markov model for low-elevation satellite-earth radio propagation channel[J]. IEEE Trans on Antennas and Propagation, 2012, 60(5): 2481-2490. |
| [13] | FONTAN F P, ESPINEIRA P M. Modelling the wireless propagation channel: a simulation approach with MATLAB[M]. Spain: John Wiley and Sons, Ltd University of Vigo, 2008. |
| [14] | ARNDT D, HEYN T, KONIG J, et al. Extended two-state narrowband LMS propagation model for S-band[C]//IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB). Seoul: IEEE, 2012: |
 2016, Vol. 45
2016, Vol. 45
