2. 北京工业大学电子信息与控制工程学院 北京 朝阳区 100124
2. College of Electronic Information and Control Engineering, Beijing University of Technology Chaoyang Beijing 100124
移动互联网业务的迅猛发展对未来移动通信系统提出更高的传输质量与系统容量要求。为此,需要研究新的网络体系架构来提高整个系统容量。研究表明,相对于传统编码、调制不到10倍的频谱效率提升以及带宽信号的几十倍传输速率的提升,缩小小区带来的频谱效率增益达到数千倍。因此,未来无线网络中,在宏基站覆盖区域内,高密度地部署各类低功率无线节点形成超密集网络(UDN),通过减小覆盖小区半径来提高频谱资源的空间复用率,是支持移动互联业务量不断增长的关键。
由于UDN技术具有提高频谱效率的巨大潜力,成为当前无线通信领域的研究热点。针对UDN小区数多、小区边界不规则以及由此带来的更复杂的切换问题,文献[1]提出了切换算法以保证移动性性能。考虑到UDN网络拓扑和干扰图样随机地动态变化,文献[2]研究了适应这些变化的网络动态部署技术。文献[3]采用随机几何理论研究推导出UDN中最佳小区部署密度及相应的基站发射功率。为了最大限度地提高UDN的网络吞吐量,文献[4]提出一种同时选择接入点路由信息以及与每条链路无线资源的联合设计方法。这些研究主要从UDN基站部署和网络层资源分配角度出发,而较少考虑如何合理利用空域资源来提高系统性能。
在UDN中网络的密集化部署使得网络节点更接近用户端,大幅度地提高了系统容量,也使得未来移动网络将使现有的小区结构微型化。这时,由于相邻基站节点传输损耗差别不大,对用户端而言可能存在多个强度相近的干扰源,从而导致更严重的小区间干扰。这需要通过小区间协调处理,解决UDN小区微型化所带来的干扰问题,最大限度地提高整个网络容量。
同时,因超密集网络小区覆盖半径较小,易于解决基站间同步和回程链路等工程实现问题,更有利于基站间协同处理以消除干扰[5]。因此,本文研究了UDN网络中干扰消除问题。首先建立了UDN空域协同波束形成的系统优化模型;并根据凸优化理论实现其最优解,即最优波束形成器;其次考虑到最优波束形成器难以工程实现的局限,采用基于信号泄漏噪声比(SLNR)的线性波束形成器来减少区间干扰,从而提高系统容量。
1 系统模型假设UDN网络有${K_t}$个基站,每个基站安装${N_m}$幅天线,总发射天线$N = \sum\limits_{m = 1}^{{K_t}} {{N_m}} $。基站覆盖区内共有${K_r}$用户,且每个用户安装单幅天线。根据用户终端的位置,将其动态划分为小区内所有用户集${{\cal C}_m} \subseteq \{ 1,{\rm{2}},\cdots ,{K_r}\} $和该集合中小区中心用户子集${{\cal D}_m} \subseteq {{\cal C}_m}$,用户集${{\cal C}_m}$包括小区中心用户和需要采用协同BF进行干扰抑制的小区边缘用户,对于不属于用户集${{\cal C}_m}$的其他用户的干扰可忽略不计,并可视作高斯背景噪声,如图 1所示。
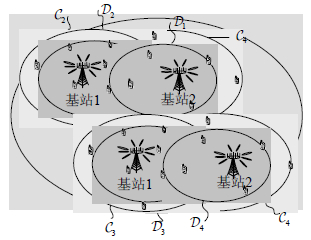 |
| 图1 超密集网络 |
考虑UDN小区下行链路,若协同基站对用户k发送信号${s_k}$,则用户k端的接收符号为:
| ${y_k} = \sum\limits_{m = 1}^{{K_t}} {{\bf{h}}_{mk}^{\rm{H}}{{\bf{C}}_{mk}}\left( {\sum\limits_{n = 1}^{{K_r}} {{{\bf{D}}_{mn}}{{\bf{w}}_{mn}}{s_n}} } \right)} + {n_k}$ | (1) |
式中,波束成形向量${{\bf{w}}_k} = {\left[{{\bf{w}}_{1k}^{\rm{T}},{\bf{w}}_{2k}^{\rm{T}},\cdots ,{\bf{w}}_{{K_t}k}^{\rm{T}}} \right]^{\rm{T}}}$,${{\bf{w}}_{mk}}$表示${m^{th}}$基站对${k^{th}}$用户的${N_m} \times 1$维波束成形矢量;高斯白噪声${n_k}$~$CN(0,\sigma _k^2)$;${{\bf{h}}_k} = {\left[{{\bf{h}}_{1k}^{\rm{T}},{\bf{h}}_{2k}^{\rm{T}},\cdots ,{\bf{h}}_{Ktk}^{\rm{T}}} \right]^{\rm{T}}}$ $ \in {\mathbb{C}^{N \times N}}$为用户k的信道衰落系数,${{\mathbf{h}}_{mk}} \in {\mathbb{C}^{{N_m}}}$为${N_m} \times 1$维信道向量。为了简化分析,定义矩阵为:
| ${{\mathbf{D}}_k} = \left[{\begin{array}{*{20}{c}} {{{\mathbf{D}}_{1k}}}&{}&0 \\ {}& \ddots &{} \\ 0&{}&{{{\mathbf{D}}_{Ktk}}} \end{array}} \right]$ | (2) |
式中,${{\mathbf{D}}_k} \in {\mathbb{C}^{N \times N}}$;$\begin{array}{*{20}{c}} {{{\mathbf{D}}_{mk}} = \left\{ \begin{gathered} {{\mathbf{I}}_{{N_m}}}{\text{ }}k \in {\mathcal{D}_m} \hfill \\ {{\mathbf{0}}_{{N_m}}}{\text{ }}其他 \hfill \\ \end{gathered} \right.} \end{array}$。则有:
| ${{\mathbf{C}}_k} = \left[{\begin{array}{*{20}{c}} {{{\mathbf{C}}_{1k}}}&{}&0 \\ {}& \ddots &{} \\ 0&{}&{{{\mathbf{C}}_{Ktk}}} \end{array}} \right]$ | (3) |
式中,${{\mathbf{C}}_k} \in {\mathbb{C}^{N \times N}}$;$\begin{array}{*{20}{c}} {{{\mathbf{C}}_{mk}} = \left\{ \begin{gathered} {{\mathbf{I}}_{{N_m}}}{\text{ }}k \in {\mathcal{C}_m} \hfill \\ {{\mathbf{0}}_{{N_m}}}{\text{ }}其他 \hfill \\ \end{gathered} \right.} \end{array}$。
由以上定义可知,${\mathbf{h}}_k^{\text{H}}{{\mathbf{D}}_k}$表示小区中心用户的传输信道,${\mathbf{h}}_k^{\text{H}}{{\mathbf{C}}_k}$表示小区所有用户的传输信道,则用户k的接收信号干扰噪声比为:
| ${\text{SIN}}{{\text{R}}_k} = \frac{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right|}^2}}}{{\sigma _k^2 + \sum\limits_{i \ne k} {{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}{{\mathbf{w}}_{mi}}} } \right|}^2}} }} $ | (4) |
又因${{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}} = {{\mathbf{D}}_{mk}}$,$\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}} \ne {\mathbf{0}}} \end{array}} \end{array}$,可得:
| ${\text{ SIN}}{{\text{R}}_k} = \frac{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right|}^2}}}{{\sigma _k^2 + \sum\limits_{i \ne k} {{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}{{\mathbf{w}}_{mi}}} } \right|}^2}} }} $ | (5) |
通常可从UDN网络中,单个用户性能和所有用户性能两个方面来衡量系统性能。若定义用户k的性能函数${g_k}({\text{SIN}}{{\text{R}}_k})$是以SINR为变量的连续、可微、严格单调递增函数,常用的用户性能函数包括信息速率(容量)等,这些函数通常为非凸函数。则基于用户性能的UDN空域协同波束形成可描述为多目标的单调优化问题[6],有:
| $\begin{gathered} \mathop {\max }\limits_{{{\mathbf{w}}_1} > {0_N},\cdots ,{{\mathbf{w}}_{{K_r}}} > 0} \{ {g_1}({\text{SIN}}{{\text{R}}_1}),{g_1}({\text{SIN}}{{\text{R}}_2}),\cdots ,{g_{{K_r}}}({\text{SIN}}{{\text{R}}_{{K_r}}})\} \hfill \\ {\text{s}}{\text{.t}}{\text{. }} \sum\limits_{k \in {\mathcal{D}_m}} {{{\left\| {{{\mathbf{w}}_{mk}}} \right\|}^2}} \leqslant {P_{{\text{tot}}}}/\left| \mathcal{A} \right| \hfill \\ {\text{SIN}}{{\text{R}}_k} = \frac{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{{\mathbf{h}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right|}^2}}}{{\sigma _k^2 + \sum\limits_{i \ne k} {{{\left| {\sum\limits_{m = 1}^{{K_t}} {{{\mathbf{h}}_{mk}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}{{\mathbf{w}}_{mi}}} } \right|}^2}} }} \hfill \\ \end{gathered} $ | (6) |
式中,$\mathcal{A}$为参与协同BF的基站集合;每个参与协同BF的基站发射功率需满足功率约束${P_m} \leqslant {P_{{\text{tot}}}}/\left| \mathcal{A} \right|$,$\forall m \in \mathcal{A}$,${P_{{\text{tot}}}}$为所有协同BF基站的总发送功率。模
型式(6)表示在满足基站发射功率和用户端接收SINR的约束条件下,寻找最优波束形成向量${{\mathbf{w}}_1},{{\mathbf{w}}_2},\cdots ,{{\mathbf{w}}_{{K_r}}}$,使得每个用户性能最佳。
为了达到用户性能域的Pareto最优边界,引入了系统性能函数如下$f({g_1}({\text{SIN}}{{\text{R}}_1}),{g_2}({\text{SIN}}{{\text{R}}_2}),\cdots ,$ ${g_{{K_r}}}({\text{SIN}}{{\text{R}}_{{K_r}}}))$,其可为系统的加权算术平均容量、加权几何平均容量等,通常为非凸函数。故基于系统性能函数的UDN空域协同波束形成可建模为单目标优化问题,有:
| $\begin{gathered} \mathop {\max }\limits_{{{\mathbf{w}}_1},{{\mathbf{w}}_2},\cdots ,{{\mathbf{w}}_{{K_r}}}} \begin{array}{*{20}{c}} {f({g_1}({\text{SIN}}{{\text{R}}_1}),{g_2}({\text{SIN}}{{\text{R}}_2}),\cdots ,{g_{{K_r}}}({\text{SIN}}{{\text{R}}_{{K_r}}}))} \end{array} \\ {\text{s}}{\text{.t}}{\text{.}} \sum\limits_{k \in {\mathcal{D}_m}} {{{\left\| {{{\mathbf{w}}_{mk}}} \right\|}^2}} \leqslant {P_{{\text{tot}}}}/\left| \mathcal{A} \right| \\ {\text{SIN}}{{\text{R}}_k} = \frac{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{{\mathbf{h}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right|}^2}}}{{\sigma _k^2 + \sum\limits_{i \ne k} {{{\left| {\sum\limits_{m = 1}^{{K_t}} {{{\mathbf{h}}_{mk}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}{{\mathbf{w}}_{mi}}} } \right|}^2}} }} \\ \end{gathered} $ | (7) |
UDN协同波束形成模型式(7)中,功率和SINR约束均有二阶锥形式的凸约束,但目标函数$f({g_1}({\text{SIN}}{{\text{R}}_1}),{g_2}({\text{SIN}}{{\text{R}}_2}),\cdots ,{g_{{K_r}}}({\text{SIN}}{{\text{R}}_{{K_r}}}))$可能是非凸函数,且对非凸性能域内的波束形成矢量${{\mathbf{w}}_1},{{\mathbf{w}}_2},\cdots ,{{\mathbf{w}}_{{K_r}}}$,${\text{SIN}}{{\text{R}}_k}$为非凸函数。因此,该优化问题是否为凸优化问题的关键在于SINR约束。为了获得该优化问题的全局最优解,下面采用根据用户业务质量(QoS)需求来设定用户SINR值的方法,将目标函数转化为凸函数,进而将单调优化问题转化为凸优化问题。
假设已知用户k的QoS需求,即可设定SINR值,则其性能函数${g_k}({\text{SIN}}{{\text{R}}_k}) = r_k^ * $,此时,用户k的SINR值${\gamma _k} = g_k^{ - 1}(r_k^ * )$,$r_1^ * \geqslant 0,1,\cdots $,$r_{{K_r}}^ * \geqslant 0$,故系统性能函数为:
| $f({g_1},{g_2},\cdots ,{g_{{K_r}}}) = \left\{ \begin{gathered} 0,\mathop {\min }\limits_{\{ k:r_k^ * > 0\} } \frac{{{g_k}}}{{r_k^ * }} \geqslant 1 \hfill \\ - \infty {\text{ }}其他 \hfill \\ \end{gathered} \right.$ | (8) |
式(8)表明,若满足用户QoS需求则系统性能函数为0,否则趋近于$ - \infty $,即可行解为空集。将式(8)代入式(7),得到如下优化问题:
| $\begin{gathered} {\text{find}} {{\mathbf{w}}_1},{{\mathbf{w}}_2},\cdots ,{{\mathbf{w}}_{{K_r}}} \\ {\text{s}}{\text{.t}}{\text{. }}\sum\limits_{k \in {\mathcal{D}_m}} {{{\left\| {{{\mathbf{w}}_{mk}}} \right\|}^2}} \leqslant {P_{{\text{tot}}}}/\left| \mathcal{A} \right| \\ \end{gathered} $ | (9) |
式中,第二项约束为${\text{SIN}}{{\text{R}}_k} \geqslant g_k^{ - 1}(r_k^ * )$的二阶锥形式;$\Re \left( {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right) $表示用户k接收信号$\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} $的实部,并且其虚部为$\Im \left( {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right) = 0$。下面利用凸优化方法求解模型式(9)的最优波束形成矢量,该式的拉格朗日函数为:
| $\begin{gathered} \mathcal{L}(\{ {{\mathbf{w}}_k}\} ,\lambda ,\mu ) = \\ \sum\limits_{m = 1}^{{K_t}} {{\mu _m}\left( {\frac{{\left| A \right|}}{{{P_{{\text{tot}}}}}}\sum\limits_{k \in {\mathcal{D}_m}}^{} {{{\left| {{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} \right|}^2}} - 1} \right)} + \\ \sum\limits_{k = 1}^{{K_r}} {{\lambda _k}\left( {1 + \frac{1}{{\sigma _k^2}}\sum\limits_{i \ne k} {{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}{{\mathbf{w}}_{mi}}} } \right|}^2}} } \right.} - \\ \left. {\frac{1}{{\sigma _k^2{\gamma _k}}}{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right|}^2}} \right) = \\ \sum\limits_{k = 1}^{{K_r}} {{\lambda _k}} - \sum\limits_{m = 1}^{{K_t}} {{\mu _m}} + \sum\limits_{m = 1}^{{K_t}} {\frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}}\sum\limits_{k \in {\mathcal{D}_m}} {{{\left| {{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} \right|}^2}} } + \\ \sum\limits_{k = 1}^{{K_r}} {\frac{{{\lambda _k}}}{{\sigma _k^2}}\sum\limits_{i \ne k} {{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}{{\mathbf{w}}_{mi}}} } \right|}^2}} } - \\ \sum\limits_{k = 1}^{{K_r}} {\frac{{{\lambda _k}}}{{\sigma _k^2{\gamma _k}}}{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right|}^2}} \\ \\ \end{gathered} $ | (10) |
式中,$\lambda ,\mu $分别为拉格朗日乘子。根据上下行链路对偶原理,引入式(10)的拉格朗日对偶函数$\mathop {\min i{\text{mize}}}\limits_{{{\mathbf{w}}_1},{{\mathbf{w}}_2},\cdots ,{{\mathbf{w}}_{{K_r}}}} \mathcal{L} = \sum\limits_{k = 1}^{{K_r}} {{\lambda _k}} - \sum\limits_{m = 1}^{{K_t}} {{\mu _m}} $,其为式(7)最优解的下界,相当于:
| $\begin{gathered} \sum\limits_{m = 1}^{{K_t}} {\frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}}\sum\limits_{k \in {\mathcal{D}_m}} {{{\left| {{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} \right|}^2}} } + \\ \sum\limits_{k = 1}^{{K_r}} {\frac{{{\lambda _k}}}{{\sigma _k^2}}\sum\limits_{i \ne k} {{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}{{\mathbf{w}}_{mi}}} } \right|}^2}} } - \\ \sum\limits_{k = 1}^{{K_r}} {\frac{{{\lambda _k}}}{{\sigma _k^2{\gamma _k}}}{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } \right|}^2}} \geqslant 0 \\ \end{gathered} $ | (11) |
将${\gamma _k} = g_k^{ - 1}(r_k^ * )$带入式(11),则式(11)的对偶可行性约束为:
| $\begin{gathered} {\gamma _k} \geqslant \frac{{\frac{{{\lambda _k}}}{{\sigma _k^2}}{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} }}{{\frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}}{{\mathbf{w}}_{mk}} + \sum\limits_{i \ne k} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } }} = \\ \mathop {\max }\limits_{{{{\mathbf{\bar w}}}_{mk}}} \frac{{\frac{{{\lambda _k}}}{{\sigma _k^2}}{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}{{{\mathbf{\bar w}}}_{mk}}} }}{{\frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}}{{{\mathbf{\bar w}}}_{mk}} + \sum\limits_{i \ne k} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}{{{\mathbf{\bar w}}}_{mk}}} } }} \\ \end{gathered} $ | (12) |
其中,引入辅助变量${{\mathbf{\bar w}}_{mk}} \in {\mathbb{C}^{{N_m} \times 1}}$实现约束${\gamma _k}$的最大化。
由此得到式(9)的拉格朗日对偶问题为:
| $\begin{gathered} \mathop {\max }\limits_{{\lambda _k}\forall k,{\mu _l}\forall l} \sum\limits_{k = 1}^{{K_r}} {{\lambda _k}} - \sum\limits_{m = 1}^{{K_t}} {{\mu _m}} \\ {\text{s}}{\text{.t}}{\text{. }}{\mu _m} \geqslant 0,{\text{ }}{\lambda _k} \geqslant 0\begin{array}{*{20}{c}} {} \end{array}\forall k,m \\ \end{gathered} $ | (13) |
该对偶问题的KKT条件为:
| $\begin{gathered} 0 = \frac{{\left| A \right|{\mu _m}}}{{{P_{{\text{tot}}}}}}{{\mathbf{w}}_{mk}} + \\ \sum\limits_{i \ne k} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} } - \\ \frac{{{\lambda _k}}}{{\sigma _k^2{\gamma _k}}}{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} \\ \end{gathered} $ | (14) |
| $\begin{gathered} \left( {\frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i = 1}^{{K_r}} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } } \right){{\mathbf{w}}_{mk}} = \\ \frac{{{\lambda _k}}}{{\sigma _k^2}}\left( {1 + \frac{1}{{{\gamma _k}}}} \right){\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}} {{\mathbf{w}}_{mk}} = \\ {\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}\frac{{{\lambda _k}}}{{\sigma _k^2}}\left( {1 + \frac{1}{{{\gamma _k}}}} \right)\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}} {{\mathbf{w}}_{mk}} \\ \end{gathered} $ | (15) |
定义标量${d_k} = \frac{{{\lambda _k}}}{{\sigma _k^2}}\frac{{(1 + {\gamma _k})}}{{{\gamma _k}}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{\mathbf{w}}_{mk}}} $,又因${{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}} = {{\mathbf{D}}_{mk}}$,等式两边乘以$\left( {\frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}} + } \right.\left. {\sum\limits_{i = 1}^{{K_r}} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } } \right)$的Moore-Penrose伪逆,得到式(9)的拉格朗日对偶问题最优解,即最优对偶波束形成矢量:
| $\begin{array}{c} {w_{mk}}{\rm{ = }}\\ {\rm{ }}{d_k}{\left( {\frac{{{\mu _m}\left| A \right|}}{{{P_{{\rm{tot}}}}}} + \sum\limits_{i = 1}^{{K_r}} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\bf{h}}_{mi}^{\rm{H}}{{\bf{C}}_{mi}}{{\bf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\bf{h}}_{mi}^{\rm{H}}{{\bf{C}}_{mi}}{{\bf{D}}_{mk}}} } } \right)^\dagger }{\bf{h}}_{mk}^{\rm{H}}{{\bf{D}}_{mk}} \end{array}$ | (16) |
由式(16)可知,最优对偶波束形成矢量${\mathbf{w}}_{mk}^{}$与式${\left( {\frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i = 1}^{{K_r}} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } } \right)^\dagger }{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}$成比例。由凸优化理论知,式(9)的最优波束形成矢量${\mathbf{w}}_{mk}^ * $等于最优对偶波束形成矢量${{\mathbf{w}}_{mk}}$乘以一个比例因子,故得最优波束形成矢量:
| $\begin{gathered} {\mathbf{w}}_{mk}^ * {\text{ = }} \\ {\left( {\frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i = 1}^{{K_r}} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } } \right)^\dagger }{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}} \\ \end{gathered} $ | (17) |
式(17)表明,最优波束形成向量和最优对偶波束形成向量具有相似的解结构,即${\mathbf{\Psi }}_{mk}^\dagger {\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}$形式,其中,${{\mathbf{\Psi }}_{mk}} = \frac{{{\mu _m}\left| A \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i = 1}^{{K_r}} {\frac{{{\lambda _i}}}{{\sigma _i^2}}{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } $。式(17)中最优波束形成矢量可写为:
| ${\mathbf{w}}_{mk}^ * = \sqrt {{p_{mk}}} {{\mathbf{\bar v}}_{mk}}$ | (18) |
式中,${{\mathbf{\bar v}}_{mk}} = \frac{{{\mathbf{\Psi }}_{mk}^\dagger {\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}}}{{\left\| {{\mathbf{\Psi }}_{mk}^\dagger {\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{D}}_{mk}}} \right\|}}$为归一化的基站m对用户k的发送波束形成导向向量;${p_{mk}}$表示基站m分配给用户k的功率。将${{\mathbf{\bar v}}_{mk}}$带入式(17),可求得分配给每个用户的功率:
| $[{p_{{m_1}}}{p_{{m_2}}} \cdots {p_{m{K_r}}}] = [{\gamma _1}\sigma _1^2{\gamma _2}\sigma _2^2 \cdots {\gamma _{{K_r}}}\sigma _{{K_r}}^2]{{\mathbf{M}}^\dagger }$ | (19) |
式中,${\mathbf{M}} \in {\mathbb{R}^{{K_r} \times {K_r}}}$,其第i,k个元素${[{\mathbf{M}}]_{ik}}$为:
| ${\left[{\mathbf{M}} \right]_{ik}} = \left\{ \begin{gathered} {\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mi}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mi}}{{{\mathbf{\bar v}}}_{mi}}} {\text{ }}i = k \hfill \\ - {\gamma _k}\left( {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mi}}{{{\mathbf{\bar v}}}_{mi}}} } \right){\text{ }}i \ne k \hfill \\ \end{gathered} \right.$ | (20) |
由上推导过程可知,式(9)的UDN协同BF通过最大化${\text{SIN}}{{\text{R}}_k}$,并满足总功率约束实现,由于系统效用函数$f({g_1}({\text{SIN}}{{\text{R}}_1}),{g_2}({\text{SIN}}{{\text{R}}_2}),,\cdots ,{g_{{K_r}}}({\text{SIN}}{{\text{R}}_{{K_r}}}))$是以SINR为变量的严格单调递增函数,最大化${\text{SIN}}{{\text{R}}_k}$相当于最大化系统效用函数,则式(9)的BF解也是式(7)的可行解,故式(7)的最优波束形成向量也可写成式(18)的形式。
3 线性次优协同波束形成器最优波束形成器式(17)中存在拉格朗日因子$\lambda $,通常难以找到一组最优$\lambda $参数实现最优波束形成。因此,基于协同BF最优解式(18)的结构特征,本文采用次优波束形成导向矢量${{\mathbf{\bar v}}_{mk}}$和最优功率分配${p_{mk}}$,来设计UDN协同波束形成器,以此逼近最优系统容量。考虑到多用户系统中,基于信号泄漏噪声比的线性波束形成器在不同信噪比条件下,均具有较好的性能,本文采用SLNR发送波束形成。UDN系统中用户k的信号泄漏噪声比为:
| ${\text{SLN}}{{\text{R}}_k} = \frac{{\frac{1}{{\sigma _k^2}}{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{{\mathbf{\bar v}}}_{mk}}} } \right|}^2}}}{{\frac{1}{{{\eta _k}}} + \sum\limits_{i \ne k} {\frac{1}{{\sigma _i^2}}{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}{{{\mathbf{\bar v}}}_{mk}}} } \right|}^2}} }}$ | (21) |
式中,参数$\{ {\eta _k}\} _{k = 1}^{{K_r}}$表示用户k的接收功率,且${\eta _k} = \frac{{{P_{{\text{tot}}}}}}{{\left| \mathcal{A} \right|\left| {{\mathcal{D}_m}} \right|}}$;$\left| {{\mathcal{D}_m}} \right|$表示服务于用户k的协同基站m包含的用户数。
式(21)中,分子$\frac{1}{{\sigma _k^2}}{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{{\mathbf{\bar v}}}_{mk}}} } \right|^2}$是标量,故可通过最小化分母,即最小化${\mathbf{B}}$,实现最大化${\text{SLN}}{{\text{R}}_k}$。为便于求解,令${\mathbf{A}} = \frac{1}{{\sigma _k^2}}{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{{{\mathbf{\bar v}}}_{mk}}} } \right|^2}$,${\mathbf{B}} = {\mathbf{\bar v}}_{mk}^{\text{H}}\frac{1}{{{\eta _k}}}{{\mathbf{\bar v}}_{mk}} + \sum\limits_{i \ne k} {\frac{1}{{\sigma _i^2}}{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}{{{\mathbf{\bar v}}}_{mk}}} } \right|}^2}} $,${\mathbf{a}} = {\mathbf{D}}_{mk}^{\text{H}} \times $${\mathbf{C}}_{mk}^{\text{H}}{{\mathbf{h}}_{mk}}$。由此构建如下优化问题:
| $\begin{gathered} \mathop {\min }\limits_{{{{\mathbf{\bar v}}}_{mk}}} \frac{{\left| \mathcal{A} \right|\left| {{\mathcal{D}_m}} \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i \ne k} {\frac{1}{{\sigma _i^2}}} {\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}{{{\mathbf{\bar v}}}_{mk}}} } \right|^2} \\ {\text{s}}{\text{.t}}{\text{.}} {\mathbf{\bar v}}_{mk}^H{\mathbf{a}} = 1 \forall k,m \\ \end{gathered} $ | (22) |
由KKT条件可得:
| $\begin{gathered} \left( {\frac{{\left| \mathcal{A} \right|\left| {{\mathcal{D}_m}} \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i \ne k} {\frac{1}{{\sigma _i^2}}} {\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } \right){{{\mathbf{\bar v}}}_{mk}} + \\ \frac{1}{{\sigma _k^2}}{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}} {{{\mathbf{\bar v}}}_{mk}} = {\mathbf{D}}_{mk}^{\text{H}}{\mathbf{C}}_{mk}^{\text{H}}{{\mathbf{h}}_{mk}} \\ \end{gathered} $ | (23) |
| $\begin{gathered} {{{\mathbf{\bar v}}}_{mk}} = {\left( {\frac{{\left| \mathcal{A} \right|\left| {{\mathcal{D}_m}} \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i{\text{ = }}1}^{{K_r}} {\frac{1}{{\sigma _i^2}}} {\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } \right)^{ - 1}} \times \\ {\mathbf{D}}_{mk}^{\text{H}}{{\mathbf{h}}_{mk}} \\ \end{gathered} $ | (24) |
则SLNR次优波束形成导向矢量为:
| ${\mathbf{\bar v}}_{mk}^{({\text{SLNR}})} = \frac{{{{{\mathbf{\bar v}}}_{mk}}}}{{{{\left\| {{{{\mathbf{\bar v}}}_{mk}}} \right\|}_2}}}$ | (25) |
下面求解分配给用户的最优功率,选择加权算术平均的系统效用函数$\sum\limits_{k \in {\mathcal{D}_m}} {{\alpha _k}{g_k}({\text{SIN}}{{\text{R}}_k})} $作为目标函数。由于采用SLNR波束形成器消除了来自其他用户的干扰,这时用户k的接收信号干扰噪声比为${\text{SIN}}{{\text{R}}_k} \approx {\text{SN}}{{\text{R}}_k} = \frac{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}\sqrt {{p_{mk}}} {\mathbf{\bar v}}_{mk}^{{\text{SLNR}}}} } \right|}^2}}}{{\sigma _k^2}}$,故总系统效用函数可写为$\sum\limits_{k \in {\mathcal{D}_m}} {{\alpha _k}{g_k}({\text{SN}}{{\text{R}}_k})} $,由此构建功率分配的凸优化问题为:
| $\begin{gathered} \mathop {\max }\limits_{{p_{jk}} \geqslant 0\begin{array}{*{20}{c}} {} \end{array}\forall k \in {\mathcal{D}_j}} \sum\limits_{k \in {\mathcal{D}_m}} {{\alpha _k}{g_k}({\text{SN}}{{\text{R}}_k})} \\ {\text{s}}{\text{.t}}{\text{. }} \sum\limits_{k \in {\mathcal{D}_m}} {{p_{mk}}} \leqslant {P_{{\text{tot}}}}/\left| \mathcal{A} \right| \forall m \\ \end{gathered} $ | (26) |
由凸优化理论可知,式(26)的拉格朗日函数为:
| $\begin{gathered} \mathcal{L} = \\ - \sum\limits_{k \in {\mathcal{D}_m}} {{\alpha _k}{g_k}\left( {\frac{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}\sqrt {{p_{mk}}} {\mathbf{\bar v}}_{mk}^{{\text{SLNR}}}} } \right|}^2}}}{{\sigma _k^2}}} \right)} + \\ \frac{1}{{{\nu _m}}}\left( {\sum\limits_{k \in {\mathcal{D}_m}} {{p_{mk}}} - {P_{{\text{tot}}}}/\left| \mathcal{A} \right|} \right) \\ \end{gathered} $ | (27) |
式中,$\frac{1}{{{\nu _m}}}$为拉格朗日乘子。令${\rho _{mk}} = {\mathbf{h}}_{mk}^{\text{H}}{{\mathbf{C}}_{mk}}{{\mathbf{D}}_{mk}}{\mathbf{\bar v}}_{mk}^{{\text{SLNR}}}$,由KKT条件可得:
| $\frac{1}{{{\nu _m}}} = {\alpha _k}{g'_k}\left( {\frac{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\rho _{mk}}\sqrt {{p_{mk}}} } } \right|}^2}}}{{\sigma _k^2}}} \right)\frac{{{\rho _{mk}}\sum\limits_{m = 1}^{{K_t}} {{\rho _{mk}}\sqrt {{p_{mk}}} } }}{{\sigma _k^2\sqrt {{p_{mk}}} }}$ | (28) |
| ${p_k} = {\left[{\frac{{\sigma _k^2}}{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\rho _{mk}}} } \right|}^2}}}{{g'}^{{\text{ - }}1}}_k\;\left( {\frac{{\sigma _k^2}}{{{\nu _m}{\alpha _k}{\rho _{mk}}\sum\limits_{m = 1}^{{K_t}} {{\rho _{mk}}} }}} \right)} \right]_ + }$ | (29) |
| ${p_{mk}} = {\left[{\frac{{\sigma _k^2}}{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\rho _{mk}}} } \right|}^2}}}{{g'}^{{\text{ - }}1\;}}_k\;\left( {\frac{{\sigma _k^2}}{{{\nu _m}{\alpha _k}{\rho _{mk}}\sum\limits_{m = 1}^{{K_t}} {{\rho _{mk}}} }}} \right)} \right]_ + }/\left| \mathcal{A} \right|$ | (30) |
式中,$\frac{{\text{d}}}{{{\text{d}}x}}{g_k}(x) = {g'_k}(x)$;${[\cdot]_{\text{ + }}}$表示用0代替负值;参数${\nu _m} \geqslant 0$。
由以上分析可知,在计算出次优波束形成导向矢量${\mathbf{\bar v}}_{mk}^{({\text{SLNR}})}$和功率分配${p_{mk}}$的基础上,可设计SLNR波束形成器,有:
| $\begin{gathered} {\mathbf{w}}_{mk}^{sub} = \sqrt {{{\left[{\frac{{\sigma _k^2}}{{{{\left| {\sum\limits_{m = 1}^{{K_t}} {{\rho _{mk}}} } \right|}^2}}}{{g'}^{{\text{ - }}1}}_k\;\left( {\frac{{\sigma _k^2}}{{{\nu _m}{\alpha _k}{\rho _{mk}}\sum\limits_{m = 1}^{{K_t}} {{\rho _{mk}}} }}} \right)} \right]}_ + }/\left| \mathcal{A} \right|} \times \\ \frac{{{{\left( {\frac{{\left| \mathcal{A} \right|\left| {{\mathcal{D}_m}} \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i{\text{ = }}1}^{{K_r}} {\frac{1}{{\sigma _i^2}}} {\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } \right)}^{ - 1}}{\mathbf{D}}_{mk}^{\text{H}}{{\mathbf{h}}_{mk}}}}{{{{\left\| {{{\left( {\frac{{\left| \mathcal{A} \right|\left| {{\mathcal{D}_m}} \right|}}{{{P_{{\text{tot}}}}}} + \sum\limits_{i{\text{ = }}1}^{{K_r}} {\frac{1}{{\sigma _i^2}}} {\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}\sum\limits_{m = 1}^{{K_t}} {{\mathbf{h}}_{mi}^{\text{H}}{{\mathbf{C}}_{mi}}{{\mathbf{D}}_{mk}}} } \right)}^{ - 1}}{\mathbf{D}}_{mk}^{\text{H}}{{\mathbf{h}}_{mk}}} \right\|}_2}}} \\ \end{gathered} $ | (31) |
下面通过仿真来验证本文的UDN空域协同波束形成器的性能。仿真参数如下:UDN网络中用户${K_r} = 4$,基站数${K_t} = 4$,每个基站安装天线${N_m} = 4$,$m = 1,2,3,4$,每个用户终端为单天线;系统效用函数采用加权最大最小公平性函数$f(g) = \min \frac{{{g_k}}}{{{\beta _k}}} $,$\forall k,k \in {K_r}$;用户性能函数为${g_k}({\text{SIN}}{{\text{R}}_k}) = $${\log _2}(1 + {\text{SIN}}{{\text{R}}_k})$;信道服从瑞利衰落,噪声方差${\sigma ^2} = 1$。图 2给出了不同数量基站协同BF的
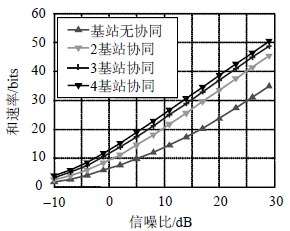 |
| 图2 基站协同BF的和速率 |
系统和容量。可以看到,与非协同BF相比,基站间协同处理后提高了UDN系统容量(和速率),且随着参与协同BF的基站数增加,UDN系统的和速率随之增大。
5 结束语本文提出了一种消除UDN小区间干扰的空域协同波束形成方法。首先构建了UDN空域协同波束形成系统模型。然后利用凸优化方法求解原协同BF问题的最优解,从理论上获得最优协同波束形成器的通用表达式。针对此最优协同波束形成器在工程中实现的局限性,提出由SLNR波束形成导向矢量和最优功率分配构成的次优波束形成器。仿真结果表明,所提出的UDN次优空域协同波束形成器能有效地抑制小区间干扰,提高系统容量。
| [1] | GODANA B E, GESBERT D. Coordinated beamforming in multicell networks with channel state information exchange delays[C]//London, UK: Institute of Electrical and Electronics Engineers Inc, 2013. |
| [2] | HUI D, AXNAS J. Joint routing and resource allocation for wireless self-backhaul in an indoor ultra-dense network[C]// London, UK: Institute of Electrical and Electronics Engineers Inc, 2013. |
| [3] | ESCUDERO G J J, HONG M, GARCIA A, et al. Interference pricing mechanism for downlink multicell coordinated beamforming[J]. IEEE Transactions on Communications, 2014, 62(6): 1871-1883. |
| [4] | DAHROUJ H, YU W. Coordinated beamforming for the multicell multi-antenna wireless system[J]. IEEE Transactions on Wireless Communications, 2010, 9(5): 1748-1759. |
| [5] | UTSCHICK W, BREHMER J. Monotonic optimization framework for coordinated beamforming in multicell networks[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 1899-1909. |
| [6] | TAPIA E M, INTILLE S S, LARSON K. Portable wireless sensors for object usage sensing in the home: Challenges and practicalities[C]//Darmstadt, Germany: Springer Verlag, 2007. |
 2016, Vol. 45
2016, Vol. 45
