信道编码识别即是根据解调后的比特流序列,辨识所采用的纠错编码类型及其对应参数,广义上还包括对交织和扰码的识别。
当前信道编码识别的主要研究成果集中于${\rm{GF}}(2)$上分组码和卷积码。文献[1, 2, 3, 4, 5]分别从代数、矩阵、优化、迭代译码等思路出发,讨论了从有噪信道识别分组码的可能性;文献[6, 7]从引入新的判决统计量的角度出发,分别将码字重量和${\rm{GF}}(2)$上的秩作为分类器;文献[8]使用Walsh-Hadamard变换,加速了误码条件下校验关系的搜索速度;文献[9]基于Grönber基理论,实现了关键方程的有效求解,进而提出了一种删除卷积码盲识别算法。
LDPC码虽属于分组码范畴,但由于其码长往往极长,构造方法多样且随机,故传统识别思路在可接受计算量内难以发挥作用。文献[10, 11, 12]通过计算后验概率对数似然比(LLR),将软解调序列与LDPC码校验关系联系在一起。文献[13]在前者基础上,进一步完善了约束关系模型,推导并量化了相应统计学特征。
以上LDPC码的研究成果均将编码识别问题弱化为一种假设检验判决问题,是在已知集合内实现码型的准确匹配,仅能适用于闭集识别应用背景。本文重点关注无误码LDPC码的开集识别问题,力求在从无误码编码序列流中,重建LDPC码稀疏校验矩阵,最终实现非合作条件下的有效译码。
1 问题描述与分析${\rm{GF}}(q)$上$(n,k)$线性分组码的识别问题为:通过接收序列${{\bf{c}}_1},{{\bf{c}}_2},{{\bf{c}}_3},\cdots $恢复出编码的生成矩阵${\bf{G}} \in {\rm{GF}}{(q)^{k \times n}}$及校验矩阵${\bf{H}} \in {\rm{GF}}{(q)^{r \times n}}$,$r = n - k$的过程,最终用于非合作条件下的信息提取,其中${\bf{c}} \in {\rm{GF}}{(q)^{1 \times n}}$称为码字。考虑问题的独立性,为简化讨论和分析,本文假设已通过使用文献[2, 3]的相关方法,实现了某$(n,k)$线性分组码码长$n$和码组起点的识别。
1.1 一般线性分组码识别问题给定${\rm{GF}}(q)$上的$(n,k)$线性分组码,存在生成矩阵$G$,使得信息${\bf{m}} \in {\rm{GF}}{(q)^{1 \times k}}$与码字${\bf{c}}$满足公式$c = mG$,称为编码约束关系(encoding restrict relationship,ERR);又存在校验矩阵$H$,与码字${\bf{c}}$满足公式$c{H^{\text{T}}} = 0$,称为校验约束关系(checking restrict relationship,CRR);将式$c = mG$代入式$c{H^{\text{T}}} = 0$可得,$mG{H^{\text{T}}} = 0$,构成公式${\bf{G}}{{\bf{H}}^{\rm{T}}} = 0$,称为正交约束关系(orthography restrict relationship,ORR)。任何试图恢复$(n,k)$码生成矩阵$G$和校验矩阵$H$的方法,都依赖于这3种约束关系。
从矩阵论角度分析可得:$(n,k)$分组码的所有${2^k}$个码字${\bf{c}}$所组成的码字空间$\mathbb{C}$,可看作由${2^k}$个信息向量${\mathbf{m}}$通过生成矩阵$G$的线性表出,若$G$由$k$个$n$维线性无关向量组成,则$G$为码字空间$\mathbb{C}$的一组基;与之相对,由于校验矩阵$H$总是与$(n,k)$分组码的所有${2^k}$个码字${\bf{c}}$正交,若$H$由$n - k$个$n$维线性无关向量组成,则由$H$张成的空间必定与码字空间$\mathbb{C}$正交,该空间称为$\mathbb{C}$的零化空间${\mathbb{C}^ \bot }$,$H$为${\mathbb{C}^ \bot }$的一组基。因此,恢复$(n,k)$分组码的生成矩阵$G$,就是寻找$(n,k)$分组码码字空间$\mathbb{C}$的某组基;而恢复校验矩阵$H$,就是寻找$(n,k)$分组码码字空间$\mathbb{C}$的零化空间${\mathbb{C}^ \bot }$的某组基。
由于有限维线性空间中的每个线性无关向量组,都可以充当此空间一组基。因此,生成矩阵$G$作为编码空间$\mathbb{C}$的一组基,并不唯一。若设定$(n,k)$分组码采用系统结构,且信息前置,则生成矩阵$G$必然满足$[I|P]$形式,其中,${\mathbf{I}}$为$k \times k$单位矩阵。通过对无误码码字${\bf{c}}$做高斯消元线性变换,获得该形式的$G$为:
| $C \to G{\text{ = }}\left[ {I|P} \right]$ | (1) |
同理,尽管编码空间$\mathbb{C}$的零化空间${\mathbb{C}^ \bot }$的基也并不唯一,但按照下式:
| $G{\text{ = }}\left[ {I|P} \right] \to H{\text{ = }}\left[ {I|P} \right]$ | (2) |
进行转换,则总可以得到一组与$G$满足ORR关系的$H$,作为${\mathbb{C}^ \bot }$的基。
综上,这种以恢复或测量码字空间的基为目标、获得编码生成矩阵$G$或校验矩阵$H$的编码识别思路,是几乎所有编码识别方法的理论基础。
1.2 LDPC码的识别信道编码识别的本质目的不仅是获取一系列编码参数,而是在此基础上实现非合作条件下的信息获取。对于一般线性分组码,$G$和$H$的恢复问题等价,按照前述计算流程,在获取$G$或$H$的基础上,结合各种代数译码方法即可展开译码,识别工作基本完成。
然而,LDPC码的识别工作则相对不同。LDPC码稀疏校验矩阵$H$的结构对该码译码性能具有决定性的影响。基于置信度传播的BP算法是LDPC码的常用译码算法,它建立在节点间信息传递具备统计独立性这一基本假设上。若$H$所对应Tanner图中存在短环,则某一节点发出的信息经过短环传递回自身,则将破坏该统计独立性假设,进而影响译码性能。因此,LDPC码在构造稀疏校验矩阵时,总是力求减少甚至完全规避短环。
因此,直接按1.1节所述方法获取的校验矩往往不可能取得好的译码效果。以IEEE 802.16e的(576,288) LDPC码为例,图 1a所示为标准中所定义的具备准循环结构的真实校验矩阵$H$,图 1b所示为根据式(2)所得的具备$[{{\mathbf{P}}^{\text{T}}}|{\mathbf{I}}]$结构的等价校验矩阵${{\mathbf{H}}_d}$。
 |
| 图1 (576,288)LDPC码的两种$H$ |
尽管$H$与${{\mathbf{H}}_d}$均满足CRR和ORR关系,都是${\mathbb{C}^ \bot }$的一组基。然而,$H$的非零元素比例占仅1%,最大行重6,4-环个数为0;而${{\mathbf{H}}_d}$的非零元素比例高达10.1%,最大行重93,4-环总数35064,显然,${{\mathbf{H}}_d}$不具备LDPC码校验矩阵的稀疏特性,无法用于译码,因此也无法实现非合作条件下的信息恢复。
综上,LDPC码识别问题与一般线性分组码识别问题不同,它不仅是寻找$(n,k)$分组码码字零化空间${\mathbb{C}^ \bot }$的任意一组基,而且是在前者基础上,恢复所有基中某组具备稀疏特性的基。本文不限定LDPC码的具体构造方法,尝试仅利用码字空间的线性相关性,实现稀疏校验矩阵$H$的重建,即对原非稀疏校验矩阵${{\mathbf{H}}_d}$的稀疏化,用以实现无误码条件下的LDPC码识别。
2 矩阵的稀疏化 2.1 2-阶行间线性变换算法非稀疏校验矩阵${{\mathbf{H}}_d}$的稀疏化就是在保证约束关系不变,校验节点与变量节点完全覆盖的前提下,尽量减少${{\mathbf{H}}_d}$中校验节点与变量节点中不必要的边。本文使用线性行变换这一手段,以非稀疏校验矩阵${{\mathbf{H}}_d}$的行重${\mathbf{W}}$作为稀疏化量度,设计了相应的矩阵稀疏化算法,称为2-阶行间线性变换。
输入:$(n,k)$分组码的非稀疏校验矩阵$H_d^{\text{T}} = \left[ {{h_1}{h_2} \cdots {h_r}} \right]$,$r = n - k$,矩阵的行重向量${\mathbf{W}} = $$\{ {w_1}{w_2} \cdots {w_r}\} $。
输出:稀疏校验矩阵${{\mathbf{H}}_s}$。
1) 取${{\mathbf{H}}_d}$中某一个行向量记做${{\mathbf{h}}_{\mathbf{i}}}$,$1 \leqslant i \leqslant r$。
2) 取${{\mathbf{H}}_d}$中另外$r - 1$个向量中的某个向量记作${{\mathbf{h}}_j}$,$j \ne i$。
3) 计算${\mathbf{h}} = {{\mathbf{h}}_i} \oplus {{\mathbf{h}}_j}$,${w'_j} = {\text{weight}}({\mathbf{h}})$。
4) 如果存在$l$使得:①${w'_j}$在$W$中最小,②${w'_l} < {w_i}$,则${{\mathbf{h}}_i} \leftarrow {{\mathbf{h}}_l}$,${w_i} \leftarrow {w'_l}$否则返回步骤2)。
5) 返回步骤1)。
6) 直至再也没有行可替换,迭代终止。
一般来说,待化简的非稀疏校验矩阵${{\mathbf{H}}_d}$形如$[{{\mathbf{P}}^{\text{T}}}|{\mathbf{I}}]$,其中,${{\mathbf{h}}_i}$表示$H$的第$i$行。实际上,该算法是一种通过对${{\mathbf{H}}_d}$做2间线性变换的矩阵稀疏化策
略,其核心思想是:在一次迭代过程中,固定${{\mathbf{H}}_d}$的某一行,并遍历其余所有行,取定两者模二加后汉明重量最小的一组结果,替换所固定的一行;重复此过程,直至在某次迭代中再也无行可换,则迭代终止,此时获取的即是稀疏化后的校验矩阵${{\mathbf{H}}_s}$。该算法计算量约为$l{r^2}n$,其中,$l$为迭代次数。
图 2记录了IEEE 802.16e (576,288)LDPC码使用该算法所得的历次迭代后的行重分布图。原始待稀疏校验矩阵${{\mathbf{H}}_d}$,平均行重58.5,最大行重68,最小行重48,经过12次稀疏化迭代后,行重降为6或7。
 |
| 图2 (576,288)LDPC码历次迭代的行重分布 |
最终的稀疏化结果如图 3所示。由图可见,其与图 1a所示的真实校验矩阵$H$是等价的,算法成功。
 |
| 图3 (576,288)LDPC稀疏化结果 |
当前,LDPC码已广泛应用于卫星、深空、无线等通信领域,具有代表性的公开标准包括IEEE 802.16e[14]、IEEE 802.11n[15]及DVB-S2[16]、GJB 7296[17],各种私有标准也层出不穷。本文使用2-阶行间线性变换算法,对它们展开测试。
图 4针对IEEE 802.16e标准进行,参数(2112,1056)。图 4a为待稀疏校验矩阵$H$,图 4b为稀疏化后的结果。由图可见,稀疏化后校验矩阵${{\mathbf{H}}_s}$已具备明显的准循环结构,经比对,与标准中描述的真实校验矩阵完全相同。
 |
| 图4 IEEE 802.16e(2112,1056) LDPC |
同理,图 5是针对IEEE 802.11n的(1944,1620)LDPC码进行仿真结果,算法证实有效。
 |
| 图5 IEEE 802.11n(1 944,1 620)LDPC |
图 6描述了针对GJB 7296-2011标准的试验情况。编码参数(992,744),该系列LDPC码由清华大学设计,已成功应用于嫦娥探月工程。图 6b为稀疏化结果,与真实矩阵完全一致。
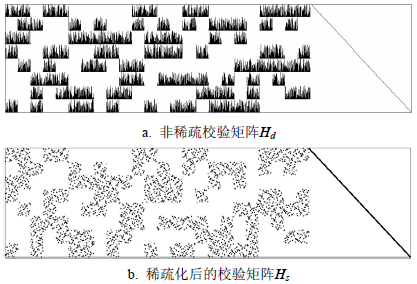 |
| 图6 GJB 7296-2011(992,744)LDPC |
以上3种LDPC标准,均属于准循环LDPC结构(QC,Quasi-Cyclic),前两种的扩展矩阵由单位阵循环移位形成,后一种的扩展矩阵被定义为一个基于伽罗华域的伪随机交织阵。
DVB-S2的校验矩阵采用了另一种结构化设计思路。其左侧为若干带状化矩阵,可在码长极长的同时控制存储量,编码效率也获得提高。图 7针对DVB-S2标准中(16200,14400)LDPC短码进行仿真,图 7b的稀疏结果呈现明显的带状形态,非零元素比由最初的$43.1\% $降为$0.19\% $,经与真实矩阵比对后证实完全相同。
 |
| 图7 DVB-S2(16200,14400)LDPC |
对于采用随机构造方式产生的LDPC码,本文选择了某商用卫星LDPC编码进行算法试验,结果如图 8所示。该矩阵右侧保持双对角形式,左侧非零元素位置随机分布。经算法处理后,非零元素个数仅占$0.17\% $,四环个数为0,可见本文的算法依然有效。
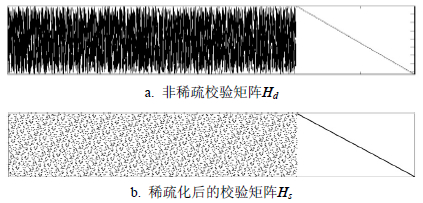 |
| 图8 某商用LDPC |
更为全面的测试显示,前述算法在某些应用场合可能失效。
图 9给出了GB20600[19]中编码参数为(7493,6096)的LDPC码校验矩阵。该标准采用信息后置设定,构造方法虽属于QC结构(扩展因子127bit),但与以往明显不同的是,左侧规模为$1\;397 \times 1\;397$的校验区,并非由每行2个$127 \times 127$的单位阵组成双对角结构,而是由每行4个$127 \times 127$的循环移位阵组成不规则的4对角结构。
 |
| 图9 GB20600(7493,6096)LDPC码校验矩阵 |
利用前述算法对非稀疏矩阵进行化简,非零元素个数仅能够由$40.69\% $降为$38.90\% $,算法可认定已失效。失效的原因与校验矩阵的特殊形态密切相关[19]。为提高编码速度,绝大多数LDPC码校验矩阵均设计为双对角形式,而2-阶行间线性变换初始时的非稀疏校验矩阵总是形如$[I|P]$,其中${\mathbf{I}}$为一$r \times r$矩阵单位阵。显然,仅仅通过两行间的线性变换,2-阶行间线性变换算法,总能够在保证校验矩阵满秩、线性关系不变的前提下,实现单位阵${\mathbf{I}}$向双对角阵的转化,在此过程中,矩阵的稀疏化就已经完成。
反观图 9所示的GB20600校验矩阵,其校验区方阵为不规则4对角,若利用原有算法,的确难以实现矩阵恢复。将原2-阶行间线性变换,拓展为p-阶行间线性变换,形成如下p-阶行间线性变换算法。
输入:$(n,k)$分组码的非稀疏校验矩阵$H_d^{\text{T}} = \left[ {{h_1}{h_2} \cdots {h_r}} \right]$,矩阵的行重向量${\mathbf{W}} = \{ {w_1}{w_2} \cdots {w_r}\} $,抽头个数$p$。
输出:稀疏校验矩阵${{\mathbf{H}}_s}$。
1) 取定抽头个数$p$,$2 \leqslant p \leqslant {p_{\max }}$。
2) 按顺序取${{\mathbf{H}}_d}$中某一个行向量记做${{\mathbf{h}}_{\mathbf{i}}}$,$1 \leqslant i \leqslant r$。
3) 取$H$另外$r - 1$个向量中的$p - 1$个向量记作${{\mathbf{h}}_{{{\mathbf{l}}_{\text{1}}}}},{{\mathbf{h}}_{{{\mathbf{l}}_{\text{2}}}}},\cdots ,{{\mathbf{h}}_{{{\mathbf{l}}_{{\mathbf{p}} - {\text{1}}}}}}$。
4) 计算${{\mathbf{h'}}_l} = {{\mathbf{h}}_{{l_1}}} \oplus {{\mathbf{h}}_{{l_2}}} \cdots \oplus {{\mathbf{h}}_{{l_{p - 1}}}}$,${w'_l} = {\text{weight}}({{\mathbf{h}}_l})$。
5) 如果存在$l$使得:① ${{\mathbf{h}}_{{l_1}}},{{\mathbf{h}}_{{l_2}}},\cdots ,{{\mathbf{h}}_{{l_{p - 1}}}}$的码重均小于${{\mathbf{h}}_l}$;② ${w'_l}$在$W$中最小;③ ${w'_l} < {w_i}$,则${{\mathbf{h}}_i} \leftarrow {{\mathbf{h'}}_l}$,${w_i} \leftarrow {w'_l}$;否则回到步骤3)。
6) 回到步骤2)。
7) 回到步骤1)。
8) 直至再也没有行可替换,迭代终止。
其中抽头个数$p$指从$r$行中一次性挑选的校验行个数。算法复杂度约为$l{r^{{p_{\max }}}}n$。
3.2 线性关系有限穷举算法前述两种算法均可以从一定程度上,实现LDPC码的校验矩阵重建。前者基于2-阶行间线性变换这一手段,适用于采用双对角结构的LDPC码;后者是对前者的加强,将运算规则拓展为p-阶行间线性变换,但仍未彻底解决稀疏校验矩阵的重建问题。
经过更为丰富的测试,本文发现:无论是2-阶行间线性变换算法还是p-阶行间线性变换算法,其基本思想均是希望通过遍历原始待稀疏校验矩阵中若干种行线性变换,穷举出有限量级内可能的稀疏化校验向量;但在实际算法进行时,第$p$层的校验节点将可能随机地等价为大于等于$p$个原始矩阵的校验节点的线性组合;而所希望的$p$个校验节点间的线性组合并未得到穷举,稀疏效果因此难以保证最优。这也解释了p-阶行间线性变换算法仍未能彻底实现矩阵稀疏化的根本原因。
基于确保校验关系得到穷举这一目标,本文形成了矩阵稀疏化通用算法:
输入:$(n,k)$分组码的非稀疏校验矩阵$H_d^{\text{T}} = \left[ {{h_1}{h_2} \cdots {h_r}} \right]$,抽头个数$p$。
输出:稀疏校验矩阵${{\mathbf{H}}_s}$。
1) 遍历抽头个数$p$,形成${\Gamma _p} = {\text{\{ }}{\mathbf{h}}_p^1,{\mathbf{h}}_p^2,{\mathbf{h}}_p^3,\cdots {\text{\} }}$。
2) 将${\Gamma _1},{\Gamma _2},\cdots ,{\Gamma _p}$中所有向量按照码重由小至大排序,并入集合$\Gamma $。
3) 按照某准则,挑选$\Gamma $中向量选入集合$\Phi $,$\Phi $所对应的矩阵即为${{\mathbf{H}}_s}$。
该算法通过穷举非稀疏校验矩阵${{\mathbf{H}}_d}$中原$r$行线性无关校验向量的部分排列组合,存储于集合${\Gamma _1},{\Gamma _2},\cdots ,{\Gamma _p}$中。此时,集合${\Gamma _1},{\Gamma _2},\cdots ,{\Gamma _p}$中包含的校验向量,从数量上远大于$r$个,从码重分布上稀疏和稠密并存。
此时的任务是从${\Gamma _1},{\Gamma _2},\cdots ,{\Gamma _p}$中仅仅挑选$r$个向量,组成集合$\Phi $,使得$\Phi $对应的矩阵满足:
1) 足够稀疏;
2) 行满秩。为此,该算法采用了如下挑选策略:首先将${\Gamma _1},{\Gamma _2},\cdots ,{\Gamma _p}$中所有向量按照码重由小到大进行排序,记做集合$\Gamma $。接着从$\Gamma $中,顺序挑选$h$放入集合$\Phi $中,每放入一个$h$,则对此时集合$\Phi $中所有向量组成的矩阵进行一次秩检测:如果矩阵行满秩,则挑选下一个$h$,再次扩充集合$\Phi $,重复前述操作;否则,从$\Phi $中剔除此$h$,而选择另一个$h$,重复前述操作。最终,当$\Phi $中向量个数达到$r$后,算法终止。
综上所述,该算法为一种确定性算法,以确保重建结果存在并局部最优。算法复杂度约为${r^{p{\;_{\max }}\; + \;2}}$,其中$2 \leqslant {p_{\max }} \ll r < n$。
通过设定${p_{\max }} = 4$,最终成功地重建了GB20600中(7493,6096)LDPC码的校验矩阵,证实了该有限穷举算法的可行性。重建结果如图 10所示。
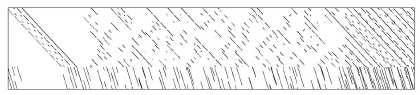 |
| 图10 GB20600(7493,6096)LDPC码校验矩阵 |
本文研究了无误码条件下LDPC码稀疏校验矩阵的重建问题。经过与一般分组码识别问题的分析与比较,将LDPC码识别问题等价为寻找LDPC码码字零化空间内某组稀疏基的数学问题,相继设计并实现了2-阶行间线性变换、p-阶行间线性变换、线性关系有限穷举在内的3种矩阵稀疏化算法。以上算法均以线性变换作为工具,以非稀疏校验矩阵的行重作为优化对象,力求实现无误码条件下,对适度码长长度LDPC码校验矩阵的有效重建。针对包括802.16e、802.11n、DVB-S2、GJB7296在内的多种LDPC标准/协议的测试结果显示,本文算法所重建的稀疏矩阵与真实校验矩阵完全相同,实现了非合作条件下的等效译码,基本验证了该算法的有效性。
对于难度更大的误码条件下LDPC码重建问题,将在后续文章中提出相应的解决方案。
| [1] | VALEMBOIS A. Detection and recognition of a binary linear code[J]. Discrete Applied Mathematics, 2001, 111(1): 199-218. |
| [2] | CHABOT C. Recognition of a code in a noisy environment [C]//Proceedings of IEEE International Symposium on Information Theory. Nice, USA: IEEE, 2007: 2211-2215. |
| [3] | BARBIER J. SICOT G, HOUCKE S. Algebraic approach for the reconstruction of linear and convolutional error correcting codes[J]. Proceedings of World Academy of Science Engineering & Technology, 2006, 2(3): 113-118. |
| [4] | CLUZEAU M, TILLICH J. On the code reverse engineering problem[C]//Proceedings of IEEE International Symposium on Information Theory. Toronto, ON, USA: IEEE, 2008: 634-638. |
| [5] | CLUZEAU M. Block code reconstruction using iterative decoding techniques[C]//Proceedings of 2006 IEEE International Symposium on Information Theory. Seattle, WA, USA: IEEE, 2006: 2269-2273. |
| [6] | 昝俊军.低码率线性分组码的盲识别[J].无线电技术,2009, 39(1): 19-24. ZAN Jun-jun. Blind recognition of low code-rate binary linear block codes[J]. Radio Engineering, 2009, 39(1): 19-24. |
| [7] | 张永光.信道编码及其识别分析[M].北京:电子工业出版社, 2010. ZHANG Yong-guang. Recognition and analyze the channel coding[M]. Beijing: Publishing House of Electronic Industry, 2010. |
| [8] | 游凌, 朱中梁. Walsh函数在解二元域方程组上的应用[J]. 信号处理, 2000, 16: 27-30. YOU Ling. The application of walsh function in resolving of GF(2) equations[J]. Signal Processing, 2000,16: 27-30. |
| [9] | 陆佩忠. 删除卷积码的盲识别[J]. 中国科学(E辑), 2005, 35(2): 173-185. LU Pei-zhong. Blind recognition of punctured convolutional codes[J]. Science in China, Series E, 2005, 35(2): 173-185. |
| [10] | 于沛东.一种利用软判决的信道编码识别新算法[J]. 电子学报, 2013 (2): 301-306. YU Pei-dong. A norei algorithm for channei coding recognition using soft decision[J]. Acta Electronica Sinica, 2013(2): 301-306. |
| [11] | XIA T, WU H C. Novel blind identification of LDPC codes using average LLR of syndrome a Postereriori probability [C]//2012 12th International Conference on ITS Telecommunications (ITST). [S.l.]: IEEE, 2012: 12-16. |
| [12] | XIA T, WU H C. Novel blind identification of LDPC codes using average LLR of syndrome a posteriori probability [C]//2012 12th International Conference on ITS Telecommunications (ITST). [S.l.]: IEEE, 2012: 12-16. |
| [13] | 包昕. 基于软解调序列的LDPC码闭集识别方法[J]. 电讯技术, 2015, 55(1): 55-60. BAO Xin. A finite set recognition algorithm of LDPC coding by using soft-demodulation sequence[J]. Telecommunication Engineering, 2015, 55(1): 55-60. |
| [14] | LAN/MAN Standards Committee of IEEE Computer Society, IEEE Microwave Theory and Techniques Society. Draft IEEE standard for local and metropolitan area networks part 16: Air interface for fixed and mobile broadband wireless access systems amendment for physical and medium access control layers for combined fixed and mobile operation in licensed bands[S]. IEEE P802.16e. New York, USA: IEEE Standards Activities Department, 2005: 472-475. |
| [15] | LAN/MAN Standards Committee of IEEE Computer Society. IEEE standard for information technology telecommunications and information exchange between systems-local and metropolitan area networks specific requirements part11: Wireless lan medium access control (MAC) and physical layer (PHY) specifications[S]. IEEE P802.11n. New York, USA: IEEE Standards Activities Department, 2009: 289-293. |
| [16] | European Broadcasting Union. Digital video broadcasting (DVB): Second generation framing structure, channel coding and modulation systems for broadcasting, interactive services, news gathering and other broadband satellite applications[S]. DVB-S2. Europe: European Telecommunications Standards Institute, 2006: 21-23. |
| [17] | 中国人民解放军总参谋部. 军用低密度奇偶校验码参数及编译码算法[S]. GJB-7296. 北京: 中国人民解放军总参谋部, 2011. The General Equipment Department of the Chinese People's Liberation Army. Parameters and algorithm of low density parity check code for military application[S]. GJB-7296. Beijing: Chinese People's Liberation Army Press, 2011. |
| [18] | 中国国家标准化管理委员会. 数字电视地面广播传输系统帧结构, 信道编码和调制[S]. GB 20600-2006. 北京: 中国标准出版社, 2007. Standardization Administration of the People's Republic of China. Digital TV terrestrial broadcasting transmission system: Frame structure, channel encoding and modulation [S]. GB 20600-2006. Beijing: China Standard Press, 2007. |
| [19] | QIN H, DIAO Q, LIN S, et al. Cyclic and quasi-cyclic LDPC codes on constrained parity-check matrices and their trapping sets[J]. IEEE Transactions on Communications, 2012, 58(5): 2648-2671. |
 2016, Vol. 45
2016, Vol. 45
