近年来,作为环境和能源问题的一种解决方案,电动汽车受到了越来越多的关注[1]。而由4个轮毂电机独立驱动的电动汽车因其独特的优势代表了汽车未来发展的方向。相对于一般的电动汽车,四轮轮毂驱动电动汽车取消了中央驱动电机以及传统部件(包括变速器、差速器、万向节和传动轴),简化了整车结构并降低了整车重量,从而减少了行车能量消耗[2]。另外,由于4个驱动轮可以单独控制,能通过直接横摆力矩控制改善车辆的侧向动态性能[3, 4, 5, 6]。
在四轮独立驱动电动汽车的研究方面,人们提出了多种基于直接横摆力矩控制的控制算法提高车身稳定性。文献[7]将滑膜控制器应用于四轮独立驱动电动汽车的车身稳定控制。文献[8, 9]提出了一种基于自适应前馈反馈控制器的轮毂电机驱动电动电动汽车的车身稳定控制。模糊逻辑控制器也被广泛应用于四轮轮毂电动汽车车身稳定的研究中[10, 11, 12]。
目前大部分针对四轮独立驱动电动汽车车身稳定性的研究都是基于四轮同时驱动进行的。但在实际应用中,存在只利用两个驱动轮的情况。如在低速行驶工况下采用双轮驱动相对四轮驱动具有更好的经济性[13, 14]。另外在单个轮毂电机失效的情况下也可以利用两个正常工作的驱动轮继续行驶以提高系统的安全性[15, 16]。虽然也有针对两轮独立驱动电动汽车车身稳定控制算法的研究[17, 18],但同时适用于两轮独立驱动和四轮独立驱动的车身稳定控制算法的研究处于空白阶段。
本文针对四轮独立驱动电动汽车在实际行驶中可能存在的两轮独立驱动和四轮独立驱动两种驱动模式,设计了一种双层控制结构,实现了电动汽车在两种驱动模式下的车身稳定控制。基于Matlab/ Simulink和CarSim软件的联合仿真也证明了本文设计的控制算法的有效性。
1 车辆模型本文的控制方法是基于8自由度的车辆模型进行设计的,车辆模型如图 1所示。这8个自由度包括纵向速度、侧向速度、横摆角速度和侧倾角组成的4个自由度以及4个车轮轮速自由度。
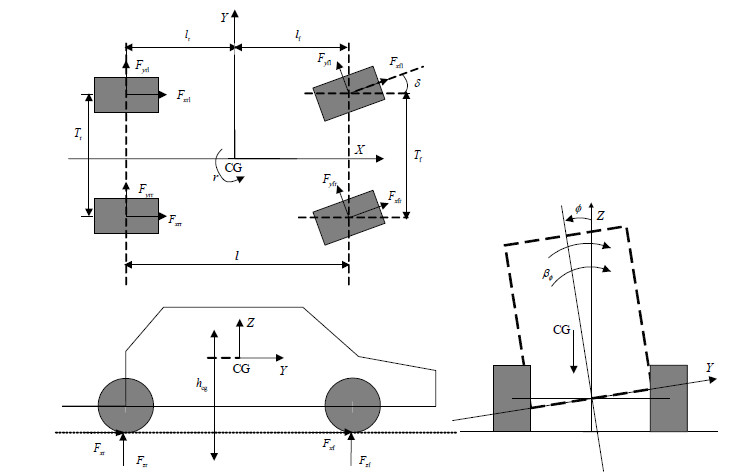 |
| 图1 8自由度车辆模型 |
车辆的纵向和侧向运动方程为:
| $m{{\dot{v}}_{x}}=({{F}_{x\text{fl}}}+{{F}_{x\text{fr}}})\cos \delta -({{F}_{y\text{fl}}}-{{F}_{y\text{fr}}})\sin \delta +{{F}_{x\text{rl}}}+{{F}_{x\text{rr}}}$ | (1) |
| $m{{\dot{v}}_{y}}=({{F}_{x\text{fl}}}+{{F}_{x\text{fr}}})\sin \delta +({{F}_{y\text{fl}}}+{{F}_{y\text{fr}}})\cos \delta +{{F}_{y\text{rl}}}+{{F}_{y\text{rr}}}$ | (2) |
式中,m表示车辆质量;${{F}_{x\text{fl}}}$、${{F}_{x\text{fr}}}$、${{F}_{x\text{fl}}}$和${{F}_{x\text{fr}}}$表示4个轮子的纵向力;${{F}_{y\text{fl}}}$、${{F}_{y\text{fr}}}$、${{F}_{y\text{fl}}}$和${{F}_{y\text{fr}}}$分别表示4个轮子的侧向力;$\delta$ 是方向盘转向角度。
横摆运动方程为:
| $\begin{align} & {{I}_{z}}\dot{r}={{l}_{\text{f}}}({{F}_{x\text{fl}}}\sin \delta +{{F}_{y\text{fl}}}\cos \delta )-\frac{{{T}_{\text{f}}}}{2}({{F}_{x\text{fl}}}\cos \delta -{{F}_{y\text{fl}}}\sin \delta )+ \\ & {{l}_{\text{f}}}({{F}_{x\text{fr}}}\sin \delta +{{F}_{y\text{fr}}}\cos \delta )+\frac{{{T}_{\text{f}}}}{2}({{F}_{x\text{fr}}}\cos \delta -{{F}_{y\text{fr}}}\sin \delta )- \\ & {{l}_{\text{r}}}({{F}_{x\text{rl}}}+{{F}_{x\text{rr}}})+\frac{{{T}_{\text{r}}}}{2}({{F}_{x\text{rr}}}-{{F}_{x\text{rl}}}) \\ \end{align}$ | (3) |
式中,Iz为车辆围绕Z轴的转动惯量;If表示前轴距;Ir表示后轴距;Tf表示前轮距;Tr表示后轮距。
侧倾运动方程为:
| ${{J}_{\text{s}x}}\ddot{\phi }=\phi (mg{{h}_{\text{cg}}}-{{\kappa }_{\phi }})-m{{h}_{\text{cg}}}{{\dot{v}}_{y}}-\dot{\phi }{{\beta }_{\phi }}$ | (4) |
车轮运动方程为:
| $\left\{ \begin{align} & {{I}_{w}}{{{\dot{\omega }}}_{\text{fl}}}={{T}_{\text{dfl}}}-{{T}_{\text{bfl}}}-{{R}_{\text{eff}}}{{F}_{x\text{fl}}} \\ & {{I}_{w}}{{{\dot{\omega }}}_{\text{fr}}}={{T}_{\text{dfr}}}-{{T}_{\text{bfr}}}-{{R}_{\text{eff}}}{{F}_{x\text{fr}}} \\ & {{I}_{w}}{{{\dot{\omega }}}_{\text{rl}}}={{T}_{\text{drl}}}-{{T}_{\text{brl}}}-{{R}_{\text{eff}}}{{F}_{x\text{rl}}} \\ & {{I}_{w}}{{{\dot{\omega }}}_{\text{rr}}}={{T}_{\text{drr}}}-{{T}_{\text{brr}}}-{{R}_{\text{eff}}}{{F}_{x\text{rr}}} \\ \end{align} \right.$ | (5) |
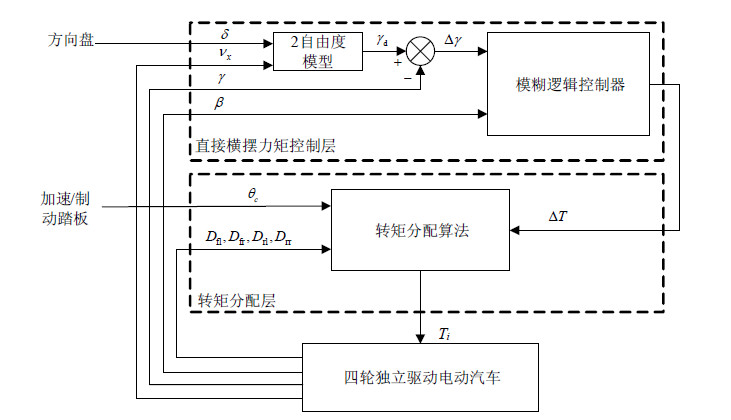 |
| 图2 双层控制结构框图 |
在车辆的运动控制中,横摆角速度和质心侧偏角因与车身的稳定状态有着紧密的联系而被作为车身稳定的控制量。而期望的横摆角速度和质心侧偏角可通过简化的2自由度车辆模型计算得到。2自由度车辆模型方程为:
| $\dot{r}=\frac{l_{\text{f}}^{2}{{C}_{\text{f}}}+l_{\text{r}}^{2}{{C}_{\text{r}}}}{{{I}_{z}}{{v}_{\text{x}}}}r+\frac{{{l}_{\text{f}}}{{C}_{\text{f}}}-{{l}_{\text{r}}}{{C}_{\text{r}}}}{{{I}_{z}}}\beta -\frac{{{l}_{\text{f}}}{{C}_{\text{f}}}}{{{I}_{z}}}\delta $ | (6) |
| $\dot{\beta }=\left( \frac{{{l}_{\text{f}}}{{C}_{\text{f}}}-{{l}_{\text{r}}}{{C}_{\text{r}}}}{mv_{x}^{2}}-1 \right)r+\frac{{{C}_{\text{f}}}+{{C}_{\text{r}}}}{m{{v}_{x}}}\beta -\frac{{{C}_{\text{f}}}}{m{{v}_{x}}}\delta $ | (7) |
| ${{r}_{\text{ref}}}=\frac{{{v}_{x}}/l}{1+\frac{m}{{{l}^{2}}}\left( \frac{{{l}_{\text{f}}}}{{{C}_{\text{r}}}}-\frac{{{l}_{\text{r}}}}{{{C}_{\text{f}}}} \right)v_{x}^{2}}\delta =\frac{{{v}_{x}}/l}{1+Kv_{x}^{2}}\delta $ | (8) |
| $K=\frac{m}{{{l}^{2}}}\left( \frac{{{l}_{\text{f}}}}{{{C}_{\text{r}}}}-\frac{{{l}_{\text{r}}}}{{{C}_{\text{f}}}} \right)$ | (9) |
直接横摆力矩控制通过在车辆的左右车轮间施加合适的驱动力或制动力从而实现车辆的车身稳定控制。因为四轮独立驱动电动汽车每个车轮的驱动力矩可单独控制,所以直接横摆力矩控制被广泛应用于四轮独立驱动电动汽车的控制中。由于汽车是一个复杂的非线性系统,本文采用模糊逻辑控制器进行附加横摆力矩的计算,其结构如图 3所示。
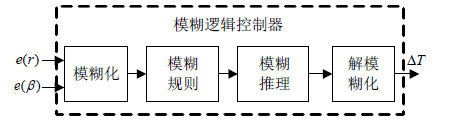 |
| 图3 模糊逻辑控制器结构框图 |
模糊逻辑控制器的两个输入为e(r)和$e(\beta )$,其中e(r)为实际横摆角速度与期望横摆角速度的差值,$e(\beta )$为实际质心侧偏角与期望质心侧偏角的差值,表达式分别为:
| $e(r)=r-{{r}_{d}}$ | (10) |
| $e(\beta )=\beta -{{\beta }_{d}}$ | (11) |
两个输入都采用7个模糊集合,其定于为:
| $\{e(r),e(\beta )\}=\{\text{NB},\text{NM},\text{NS},\text{ZO},\text{PS},\text{PM},\text{PB}\}$ | (12) |
7个语言值为:负大(NB)、负中(NM)、负小(NS)、零(ZE)、正小(PS)、正中(PM)和正大(PB)。两个输入e(r)和$e(\beta )$采用相同的隶属度函数,如图 4所示。
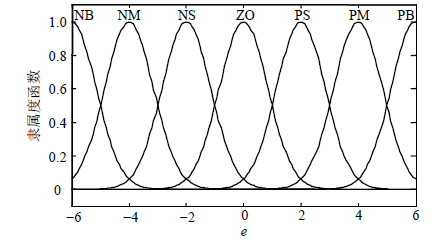 |
| 图4 隶属度函数 |
模糊控制器的输出为$\text{ }\!\!\Delta\!\!\text{ }T$为附加横摆力矩,与两个输入采用同样的隶模糊集合和隶属度函数。模糊规则表是反映输入与输出关系的一组规则,模糊规则可通过所设计系统的已有的知识得到。本文的模糊规则通过已有的专家知识和线下仿真得到,如表 1所示。
| 表1 模糊规则表 |
表 1中,本文设计的模糊规则表共包含49条规则,具体规则描述如下:
1) If e(r)is NB and $e(\beta )$isNB then U is NB
2) If e(r)is NB and $e(\beta )$isNM then U is NB
$\vdots $
49) If e(r)is NB and $e(\beta )$isNM then U is NB
2.2 力矩分配层 在力矩分配层,本文设计了同时适用于两轮独立驱动和四轮独立驱动的力矩分配算法。首先需要对每个车轮的工作状态进行定义,有:
| ${{D}_{i}}=\left\{ \begin{matrix} 0 & 从动轮 \\ 1 & 驱动轮 \\ \end{matrix} \right.$ | (12) |
| ${T}'=\left\{ \begin{matrix} K{{\theta }_{C}} & 四轮驱动 \\ 2K{{\theta }_{C}} & 两轮驱动 \\ \end{matrix} \right.$ | (13) |
式中,${T}'$表示每个车轮的期望驱动力矩;${{\theta }_{C}}$是加速踏板深度;K是反映加速踏板和参考驱动力矩之间对应关系的常数。从式(13)可以看出,在两轮独立驱动模式下每个驱动轮的参考驱动力矩为四轮独立驱动模式下的2倍,从而使总的驱动力矩在两种模式下是相等的。图 2中所示的力矩分配算法为:
| $\left\{ \begin{align} & {{T}_{\text{fl}}}^{\prime }={{D}_{\text{fl}}}({T}'+\text{ }\!\!\Delta\!\!\text{ }T) \\ & {{T}_{\text{fr}}}^{\prime }={{D}_{\text{fr}}}({T}'-\text{ }\!\!\Delta\!\!\text{ }T) \\ & {{T}_{\text{rl}}}^{\prime }={{D}_{\text{rl}}}({T}'+\text{ }\!\!\Delta\!\!\text{ }T) \\ & {{T}_{\text{rr}}}^{\prime }={{D}_{\text{rr}}}({T}'-\text{ }\!\!\Delta\!\!\text{ }T) \\ \end{align} \right.$ | (14) |
式中,${{T}_{\text{fl}}}^{\prime }$、${{T}_{\text{fr}}}^{\prime }$、${{T}_{\text{fl}}}^{\prime }$和${{T}_{\text{fr}}}^{\prime }$分别表示4个车轮的参考驱动力矩。为了防止参考驱动力矩超出电机的最大值${{T}_{\text{max}}}$,最终给每个电驱动系统的力矩设定值为:
| ${{T}_{i}}=\min \{\text{ }\!\!|\!\!\text{ }{{T}_{i}}^{\prime }|,{{T}_{\max }}\}\text{sign}({{T}_{i}}^{\prime })$ | (15) |
本文利用Matlab/Simulink和CarSim进行联合仿真分别在两轮独立驱动模式下和四轮独立驱动模式下对所设计算法进行了验证。CarSim是针对汽车动态控制的多自由度非线性仿真软件,因其仿真结果与实车实验有着较高的一致性,被广泛应用于汽车的设计和演技中。本文仿真所用车辆的参数取值如表 2所示,仿真的初始车速为80 km/h,方向盘转角如图 5所示。
| 表2 车辆参数表 |
 |
| 图5 方向盘转角 |
在四轮独立驱动模式下,所有4个车轮的驱动力矩都可以控制,其仿真结果如图 6、图 7和图 8所示。
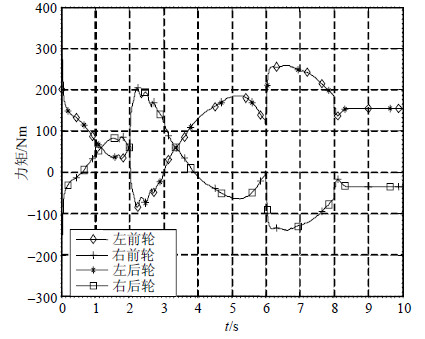 |
| 图6 四轮独立驱动模式下的驱动力矩 |
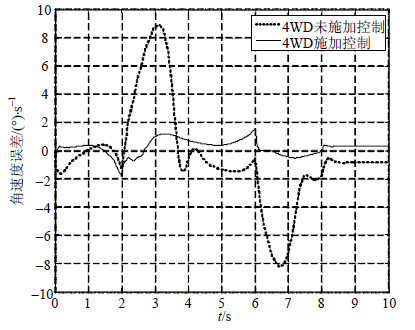 |
| 图7 四轮独立驱动模式下的横摆角速度误差 |
 |
| 图8 四轮独立驱动模式下的质心侧偏角 |
图 6为4个车轮的驱动力矩仿真结果,4个车轮的驱动力矩都处于受控的状态,且同一侧的车轮的驱动力矩是一致的,而在转向时,施加在左侧车轮和右侧车轮的附加力矩是相反的。图 7为四驱模式下横摆角速度误差的仿真结果,通过与未施加控制算法的控制效果对比可以看出,采用本文控制算法后的横摆角速度误差e(r)趋近于0,控制效果有着比较明显的改善。图 8为四轮独立驱动模式下质心侧偏角的仿真结果,可以看出相对未施加控制控制算法的控制效果,采用本文控制算法后质心侧偏角也有一定程度的改善。
3.2 两轮独立驱动模式仿真在两轮独立驱动模式下,采用两个后轮为驱动轮进行仿真,两个前轮为从动轮。采用两个前轮驱动的仿真结果与两个后轮驱动的仿真结果类似,本文中不在赘述。采用两个后轮为驱动轮的仿真结果如图 9~图 11所示。图 9为4个车轮的驱动力矩仿真结果,从图中可以看出两个前轮作为从动轮其驱动力矩为零,两个后轮的驱动力矩处于受控状态,其趋势与图 6四轮独立驱动模式下相似,但幅度更大。
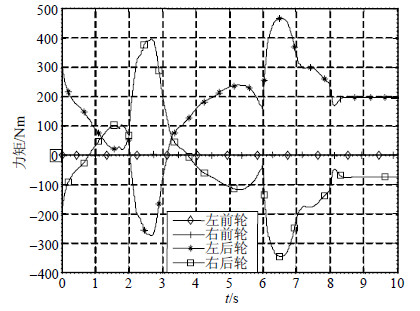 |
| 图9 两轮独立驱动模式下的驱动力矩 |
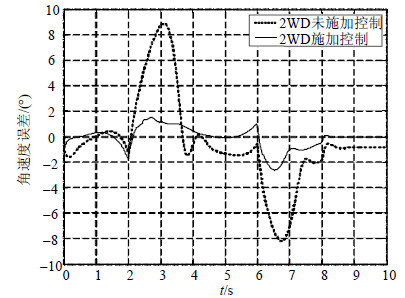 |
| 图10 两轮独立驱动模式下的横摆角速度误差 |
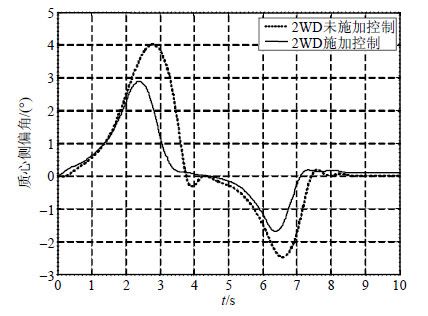 |
| 图11 两轮独立驱动模式下的质心侧偏角 |
图 10为两轮独立驱动模式下横摆角速度误差的仿真结果,从图中可以看出,采用本文控制算法后,相对于未施加控制算法的横摆角速度误差有比较明显的改善。图 11为两轮驱动模式下质心侧偏角的仿真结果,从图中可以看出,采用本文控制算法后在横摆角速度改善明显的情况下,质心侧偏角也有一定程度的改善。
4 结 论本文以四轮独立驱动电动汽车为研究对象,设计了同时适用于四轮独立驱动模式和两轮独立驱动模式的车身稳定控制算法。通过仿真结果可以看出,本文设计的车身稳定算法不论是在四轮独立驱动模式下,还是两轮独立驱动模式下,都能在明显改善横摆角速度控制效果的同时对质心侧偏角也有相应的改善,实现车身的稳定控制。本文的研究成果对于提高四轮独立驱动电动汽车的行驶安全有着积极的意义。
| [1] | MAEDA K, FUJIMOTO H, HORI Y. Four-wheel driving-force distribution method based on driving stiffness and slip ratio estimation for electric vehicle with in-wheel motors[C]//Vehicle Power and Propulsion Conference (VPPC), 2012 IEEE. Seoul, Korea: IEEE, 2012: 1286-1291. |
| [2] | 李刚, 宗长富. 四轮独立驱动轮毂电机电动汽车研究综述[J]. 辽宁工业大学学报(自然科学版), 2014, 34(1): 47-52. LI Gang, ZONG Chang-fu. Review on electric vehicle with four-wheel independent drive in-wheel motors[J]. Journal of Liaoning Institute of Technology (Natural Science Edition), 2014, 34(1): 47-52. |
| [3] | DEMIRCI M, GOKASAN M. Adaptive optimal control allocation using Lagrangian neural networks for stability control of a 4WS-4WD electric vehicle[J]. Transactions of the Institute of Measurement and Control, 2013, 35(8): 1139-1151. |
| [4] | KIM D, HWANG S, KIM H. Vehicle stability enhancement of four-wheel-drive hybrid electric vehicle using rear motor control[J]. IEEE Transactions on Vehicular Technology, 2008, 57(2): 727-735. |
| [5] | SAKAI S, SADO H, HORI Y. Motion control in an electric vehicle with four independently driven in-wheel motors[J]. Transactions on Mechatronics, IEEE/ASME, 1999, 4(1): 9-16. |
| [6] | TAHAMI F, FARHANGI S, KAZEMI R. A fuzzy logic direct yaw-moment control system for all-wheel-drive electric vehicles[J]. Vehicle System Dynamics, 2004, 41(3): 203-221. |
| [7] | HASAN M M A E, EKTESABI M, KAPOOR A. A suitable electronic stability control system using sliding mode controller for an in-wheel electric vehicle[J]. Lecture Notes in Engineering and Computer Science, 2013, 2202: 152-158. |
| [8] | NAM K, FUJIMOTO H, HORI Y. Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors[J]. IEEE Transactions on Vehicular Technology, 2012, 61(5): 1972-1985. |
| [9] | MA H. Finite-model adaptive control using WLS-like algorithm[J]. Automatica, 2007, 43(4): 677-684. |
| [10] | TAHAMI F, FARHANGI S, KAZEMI R. A fuzzy logic direct yaw-moment control system for all-wheel-drive electric vehicles[J]. Vehicle System Dynamics, 2004, 41(3): 203-221. |
| [11] | BOADA B L, BOADA M, DIAZ V. Fuzzy-logic applied to yaw moment control for vehicle stability[J]. Vehicle System Dynamics, 2005, 43(10): 753-770. |
| [12] | WANG X, FU M, YANG Y, et al. Lateral control of autonomous vehicles based on fuzzy logic[C]// Control and Decision Conference (CCDC), 2013 25th Chinese.Guiyang: IEEE, 2013:237-242. |
| [13] | 余卓平, 张立军, 熊璐. 四驱电动车经济性改善的最优转矩分配控制[J]. 同济大学学报(自然科学版), 2005, 33(10): 1355-1361. YU Zhuo-ping, ZHANG Li-jun, XIONG Lu. Optimized torque distribution control to achieve higher fuel economy of 4WD electric vehicle with four in-wheel motors[J]. Journal of Tongji University (Natural Science), 2005, 33(10): 1355-1361. |
| [14] | GU J, OUYANG M, LU D, et al. Energy efficiency optimization of electric vehicle driven by in-wheel motors[J]. International Journal of Automotive Technology, 2013, 14(5): 763-772. |
| [15] | 郑汉耕. 四轮轮毂电动车电驱动系统失效控制研究[D]. 成都: 电子科技大学, 2013. ZHENG Han-geng. Research on electric drive system failure control of four in-wheel driven electric vehicle[D]. Chengdu: University of Electronic Science and Technology of China, 2013. |
| [16] | XIN X, ZHENG H, XU H, et al. Control strategies for four in-wheel driven electric vehicles when motor drive systems fail[C]//American Control Conference (ACC), 2014. Portland, OR: IEEE, 2014: 885-890. |
| [17] | NADERI P, MIRSALIM M, BATHAEE S. Driving/regeneration and stability enhancement for a two-wheel-drive electric vehicle[J]. International Review of Electrical Engineering (IREE), 2009, 4(1): 57-65. |
| [18] | NIASAR A H, MOGHBELI H, KAZEMI R. Yaw moment control via emotional adaptive neuro-fuzzy controller for independent rear wheel drives of an electric vehicle[C]//Proceedings of 2003 IEEE Conference on Control Applications, 2003, CCA 2003. [S.l.]: IEEE, 2003: 380-385. |
 2016, Vol. 45
2016, Vol. 45
