自从作为先驱的OGY法[1]问世以来,人们就开始不断地研究适用于不同混沌系统的各种混沌控制方法,如脉冲控制法[2]、分数阶控制器[3]、无抖振滑模控制法[4]、递归反步非线性控制器[5]、双T凹槽滤波器[6]、自适应时间延迟反馈法[7]等,来控制碰撞振动系统、重新调节的Chen系统、Lorenz系统、Lorenz- Stenflo等系统中的混沌。
电压控制型Buck变换器在电力电子电路领域中得到了广泛的应用,其开关的高频切换作用及电路元件的非线性特性使得该分段光滑物理系统非常复杂,在某些电路参数条件下,存在倍周期分岔、边界碰撞分岔、切分岔、Hopf分岔、共存吸引子和混沌等非线性现象[8,9,10]。变换器在实际运行过程中会出现一些不良状况,如刺耳的电磁噪声、控制系统的间歇振荡和临界运行的突然崩溃等,这些不良状况是其工作在混沌状态的外部表现形式[11,12]。因此寻求有效的混沌控制方法将变换器的混沌状态控制在周期轨道上具有重要的意义。为了控制变换器中的混沌,国内外学者已经研究了一些方法,如模糊逻辑法[13]、冲洗滤波器[14]、改善关联性法[15]、参数共振微扰法及其改进法[16,17]、时间延迟反馈法[18,19]、OGY改进法[20]和打靶法[21]等。参数共振微扰法及其改进法属于开环控制,结构简单,需要调整扰动振幅$f$和频率$\omega $这两个参数,但在将混沌状态控制到周期状态的整个过程中,不能保证控制过程的稳定性,控制器的输出也始终不为零。时间延迟反馈法需要调整延迟时间$\tau $和控制强度k这两个参数。参数共振微扰法及其改进法和时间延迟反馈法都不需要预先确定期望的目标轨道。OGY法及其改进法和打靶法都需要预先确定期望的目标轨道。
本文通过结合状态反馈和参数扰动的思想提出了一种混合控制策略,并采用该策略实现了电压控制型Buck变换器的混沌控制。首先对电压控制型Buck变换器的数学模型,分析了输入电压变化时输出电压的分岔图和混沌状态的庞加莱截面。然后对模型施加混合控制策略,通过分析外部可调参数变化时输出电压的分岔图、周期状态的相图、周期状态的电感电流波形、周期状态的输出电压波形、周期状态的开关逻辑图,验证了该混合控制策略的有效性。该策略属于闭环控制,能够保证控制过程的稳定性,不需要预先确定期望的目标轨道,不依赖于电压控制型Buck变换器的内部电路参数,施加混合控制策略后变换器所处的周期轨道数只与一个外部可调参数的大小有关。本文的研究结果为实现变换器的混沌控制提供了一种有效的方法。
1 电压控制型Buck变换器数学模型图 1表示电压控制型Buck变换器,它由一个电阻R、一个电感L、一个电容G、一个开关G和一个二极管D组成[22]。其中开关G由误差放大器A1和比较器A2组成的反馈回路控制。
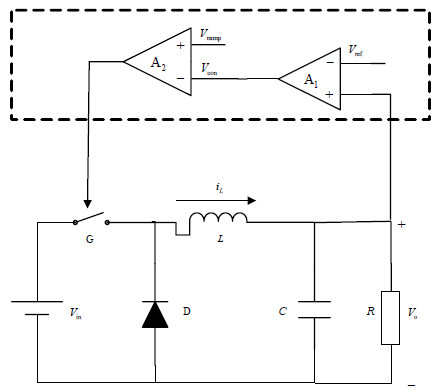 |
| 图1 电压控制型Buck变换器 |
假定电压控制型Buck变换器工作于连续导通模式(CCM),即电感电流${{i}_{\text{L}}}$不会降为0。由图 1的虚框部分可知,误差放大器A1通过放大输出电压${{V}_{\text{o}}}$与参考电压${{V}_{\text{ref}}}$之间的误差,得到控制电压${{V}_{\text{con}}}$为:
| ${{V}_{\text{con}}}(t)=A[{{V}_{\text{o}}}(t)-{{V}_{\text{ref}}}]$ | (1) |
| $\left\{ \begin{matrix} s=1\text{ }\begin{matrix} \text{ } & {{V}_{\text{ramp}}}>{{V}_{\text{con}}} \\ \end{matrix} \\ s=0\text{ }\begin{matrix} {} & {{V}_{\text{ramp}}}<{{V}_{\text{con}}} \\ \end{matrix} \\ \end{matrix} \right.$ | (2) |
| ${{V}_{\text{ramp}}}(t)={{V}_{\text{L}}}+({{V}_{\text{H}}}-{{V}_{\text{L}}})\left(\frac{t}{T}\bmod 1 \right)$ | (3) |
式中,${{V}_{\text{H}}}$和${{V}_{\text{L}}}$分别为${{V}_{\text{ramp}}}$的上限电压和下限电压;T为开关周期,即锯齿波电压${{V}_{\text{ramp}}}$的周期。
本文取电感电流iL和输出电压Vo作为状态变量。当开关G导通,二极管D截止时,电压控制型Buck变换器的状态方程为:
| ${{\dot{i}}_{\text{L}}}=\frac{-{{V}_{\text{o}}}}{L}+\frac{{{V}_{\text{in}}}}{L}{{\dot{V}}_{\text{o}}}=\frac{{{i}_{\text{L}}}}{C}-\frac{{{V}_{\text{o}}}}{RC}$ | (4) |
式中,${{V}_{\text{in}}}$为输入电压。当开关G截止,二极管D导通时,电压控制型Buck变换器的状态方程为:
| ${{\dot{i}}_{\text{L}}}=\frac{-{{V}_{\text{o}}}}{L},\ {{\dot{V}}_{\text{o}}}=\frac{{{i}_{\text{L}}}}{C}-\frac{{{V}_{\text{o}}}}{RC}$ | (5) |
将开关G导通截止的信号值s加入式(4)和式(5),得到控制前电压控制型Buck变换器的数学模型为:
| ${{\dot{i}}_{\text{L}}}=\frac{-{{V}_{\text{o}}}}{L}+\frac{{{V}_{\text{in}}}}{L}s,{{\dot{V}}_{\text{o}}}=\frac{{{i}_{\text{L}}}}{C}-\frac{{{V}_{\text{o}}}}{RC}$ | (6) |
控制前电压控制型Buck变换器的电路参数:${{V}_{\text{in}}}=18\sim 38\ \text{V}$,$R=22\ \Omega$,$L=20\ \text{mH}$,$C=47\ \mu \text{F}$,$T=400\ \mu \text{s}$,${{V}_{\text{ref}}}=11.3\ \text{V}$,A=8.4,${{V}_{\text{H}}}=8.2\ \text{V}$,${{V}_{\text{L}}}=3.8\ \text{V}$[23,24]。以输入电压${{V}_{\text{in}}}$为分岔参数输出电压${{V}_{\text{o}}}$的分岔图(${{V}_{\text{in}}}=18$~$38\ \text{V}$),如图 2所示。由图 2可知,当${{V}_{\text{in}}}>33\ \text{V}$时,电压控制型Buck变换器处于混沌状态。
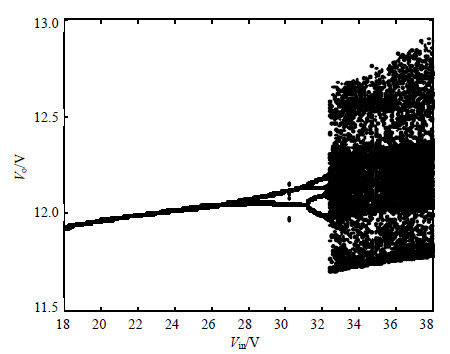 |
| 图2 分岔图(${{V}_{\text{in}}}=18\sim 38\ \text{V}$) |
下文采用混沌状态的庞加莱截面验证了电压控制型Buck变换器中混沌的存在性。也可以采用李雅普诺夫指数谱来验证该存在性,见文献[25,26,27],本文不再详述。由图 3可知,混沌状态的庞加莱截面(以输入电压${{V}_{\text{in}}}=35\ \text{V}$为例)表现为具有一定结构在相空间占据有限范围的奇怪吸引子。奇怪吸引子是指具分形结构的吸引子,在奇怪吸引子外的一切运动都趋向(被吸引)到吸引子,属于“稳定”的方向;一切到达奇怪吸引子内的运动都互相排斥,对应于“不稳定”方向。由图 3所示的奇怪吸引子可知,当电压控制型Buck变换器处于混沌状态时,该变换器是有界的,即该混沌系统的轨线在相空间中有界。因此可以通过设计控制策略将该变换器中的不稳定周期轨道(UPO)控制在稳定的周期轨道上,消除系统中的混沌。
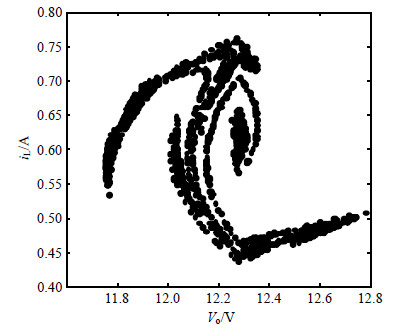 |
| 图3 混沌状态的庞加莱截面(${{V}_{\text{in}}}=35\ \text{V}$) |
考虑一个二维混沌系统:
| $\left\{ \begin{align} & \frac{\text{d}{{x}_{1}}}{\text{d}t}={{f}_{1}}({{x}_{1}},{{x}_{2}},t)\\ & \frac{\text{d}{{x}_{2}}}{\text{d}t}={{f}_{2}}({{x}_{1}},{{x}_{2}},t)\\ \end{align} \right.$ | (7) |
| $\left\{ \begin{align} & {{{\tilde{f}}}_{1}}({{x}_{1}},{{x}_{2}},t)=(1-\gamma){{f}_{1}}({{x}_{1}},{{x}_{2}},t)+\gamma {{x}_{1}} \\ & {{{\tilde{f}}}_{2}}({{x}_{1}},{{x}_{2}},t)=(1-\gamma){{f}_{2}}({{x}_{1}},{{x}_{2}},t)+\gamma {{x}_{2}} \\ \end{align} \right.$ | (8) |
式中,$\gamma $表示外部可调参数,取值范围为0~1;$\gamma {{x}_{1}}$、$\gamma {{x}_{2}}$为状态反馈;$(1-\gamma){{f}_{1}}({{x}_{1}},{{x}_{2}},t)$,$(1-\gamma){{f}_{2}}({{x}_{1}},{{x}_{2}},t)$为参数扰动。将式(8)代入式(7),即用${{\tilde{f}}_{1}}({{x}_{1}},{{x}_{2}},t)$,${{\tilde{f}}_{2}}({{x}_{1}},{{x}_{2}},t)$分别代替式(7)中的${{f}_{1}}({{x}_{1}},{{x}_{2}},t)$,${{f}_{2}}({{x}_{1}},{{x}_{2}},t)$,得到受控的二维混沌系统为:
| $\left\{ \begin{align} & \frac{\text{d}{{x}_{1}}}{\text{d}t}={{{\tilde{f}}}_{1}}({{x}_{1}},{{x}_{2}},t)=(1-\gamma){{f}_{1}}({{x}_{1}},{{x}_{2}},t)+\gamma {{x}_{1}} \\ & \frac{\text{d}{{x}_{2}}}{\text{d}t}={{{\tilde{f}}}_{2}}({{x}_{1}},{{x}_{2}},t)=(1-\gamma){{f}_{2}}({{x}_{1}},{{x}_{2}},t)+\gamma {{x}_{2}} \\ \end{align} \right.$ | (9) |
由式(9)可知,当γ=0时,${{\tilde{f}}_{2}}({{x}_{1}},{{x}_{2}},t)$,${{\tilde{f}}_{1}}({{x}_{1}},{{x}_{2}},t)$分别退化为${{f}_{1}}({{x}_{1}},{{x}_{2}},t)$,${{f}_{2}}({{x}_{1}},{{x}_{2}},t)$,即式(9)退化为式(7),此时式(9)自由演化。当$0 <\gamma <1$时,此时式(9)在受控状态下演化。混沌系统式(7)隐含着各种不稳定的周期轨道,通过施加混合控制策略,可将原混沌系统中存在的不稳定周期轨道(UPO)控制到稳定的周期轨道上(可参考文献[28])。给出如下定理。
定理1 受控混沌系统式(9)与原混沌系统式(7)具有相同的p周期轨道。
证明原系统式(7)经过p次迭代后为:
| $x_{1}^{(p+1)}=f_{1}^{(p)},\text{ }x_{2}^{(p+1)}=f_{2}^{(p)}\text{ }$ | (10) |
式中,p为某个正整数;$f_{1}^{(p)}$、$f_{2}^{(p)}$分别为映射${{f}_{1}}$、${{f}_{2}}$的p次复合函数。这里,迭代是指一种不断用变量的旧值代替新值的反馈过程。当原系统式(7)有p周期轨道时,则$x_{1}^{(p)}={{x}_{1}}\text{,}x_{2}^{(p)}={{x}_{2}}$,那么由式(10)可得原系统式(7)的p周期轨道满足的方程为:
| $\text{d}{{x}_{1}}/\text{d}t=f_{1}^{(p)}\text{,d}{{x}_{2}}/\text{d}t=f_{2}^{(p)}$ | (11) |
同理,当受控系统式(9)有p周期轨道时,由式(8)得其p周期轨道满足的方程为:
| $\left\{ \begin{align} & \frac{\text{d}{{x}_{1}}}{\text{d}t}=(1-\gamma)f_{1}^{(p)}+\gamma x_{1}^{(p)} \\ & \frac{\text{d}{{x}_{2}}}{\text{d}t}=(1-\gamma)f_{2}^{(p)}+\gamma x_{2}^{(p)} \\ \end{align} \right.$ | (12) |
即:
| $\text{d}{{x}_{1}}/\text{d}t={{\tilde{f}}_{1}}^{(p)}\text{,d}{{x}_{2}}/\text{d}t={{\tilde{f}}_{2}}^{(p)}$ | (13) |
由式(11)、式(13)可知,原系统式(7)和受控系统式(9)的p周期轨道满足相同的方程,定理1得证。
下文通过数值仿真验证该策略的有效性并分析稳定后p周期轨道对应的外部可调参数γ的稳定域。
4 采用混合控制策略控制电压控制型Buck变换器中的混沌由于${{i}_{\text{L}}}$、${{V}_{\text{o}}}$是电压控制型Buck变换器的状态变量,即${{x}_{1}}={{i}_{\text{L}}}$,${{x}_{2}}={{V}_{\text{o}}}$,式(6)可写为:
| $\left\{ \begin{align} & {{f}_{1}}({{i}_{\text{L}}},{{V}_{\text{o}}},t)=\frac{-{{V}_{\text{o}}}}{L}+\frac{{{V}_{\text{in}}}}{L}s \\ & {{f}_{2}}({{i}_{\text{L}}},{{V}_{\text{o}}},t)=\frac{{{i}_{\text{L}}}}{C}-\frac{{{V}_{\text{o}}}}{RC} \\ \end{align} \right.$ | (14) |
那么控制后电压控制型Buck变换器的数学模型为:
| $\left\{ \begin{align} & {{{\dot{i}}}_{\text{L}}}=\frac{-{{V}_{\text{o}}}}{L}+\frac{{{V}_{\text{in}}}}{L}s-\gamma \left(\frac{-{{V}_{\text{o}}}}{L}+\frac{{{V}_{\text{in}}}}{L}s-{{i}_{\text{L}}} \right)\\ & {{{\dot{V}}}_{\text{o}}}=\frac{{{i}_{\text{L}}}}{C}-\frac{{{V}_{\text{o}}}}{RC}-\gamma \left(\frac{{{i}_{\text{L}}}}{C}-\frac{{{V}_{\text{o}}}}{RC}-{{V}_{\text{o}}} \right)\\ \end{align} \right.$ | (15) |
由式(15)可以设计施加混合控制策略后电压控制型Buck变换器的电路框图,如图 4所示。端口1(Out1),端口2(Out2)的输出信号分别为${{i}_{\text{L}}}$和${{V}_{\text{o}}}$。端口3(Out3),端口4(Out4)的输出信号分别为${{V}_{\text{ramp}}}$和${{V}_{\text{con}}}$,通过对这两个电压取差可得开关G导通截止的信号值s。增益模块“gamma”表示外部可调参数γ。式(15)中的两个微分方程可以由两个积分模块来实现。根据图 4执行仿真,仿真区间为$t=[0,0.4]\ \text{s}$,并在$t=0.1\ \text{s}$时开始施加混合控制策略。图 5表示以外部可调参数γ为分岔参数输出电压Vo的分岔图。图 6为图 5的局部放大图。由图 5和图 6可知,随着外部可调参数γ的减小,混合控制策略能够将电压控制型Buck变换器的混沌状态控制在周期1、2、4、8轨道上。
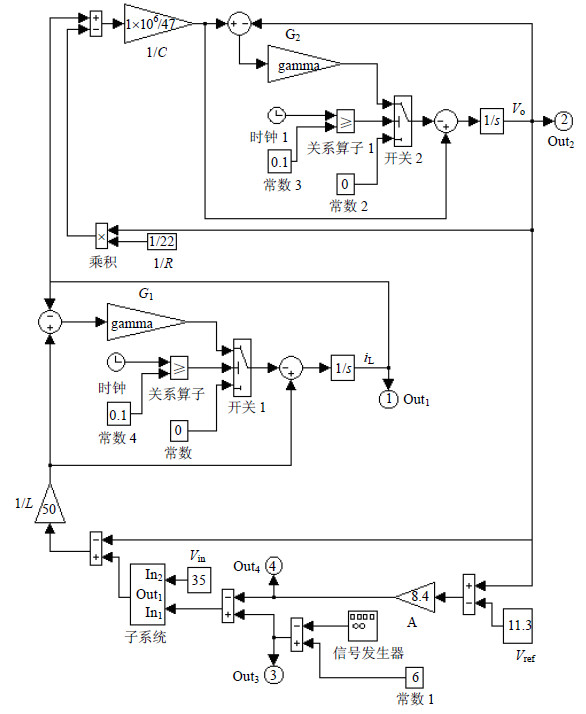 |
| 图4 施加混合控制策略后电压控制型Buck变换器的电路框图 |
 |
| 图5 以外部可调参数γ为分岔参数输出电压V.的分岔图($\gamma =[0,1]$) |
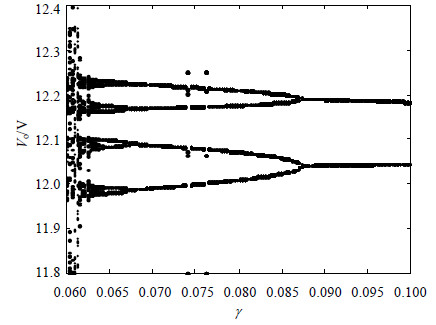 |
| 图6 图 5的局部放大图($\gamma =[0.06,0.1]$) |
下文通过分析图 7a~图 7d、图 8~图 11,可以研究施加混合控制策略后,当外部可调参数γ取具体的不同值时,电压控制型Buck变换器的非线性动力学行为。
 |
| 图7 控制后周期1、2、4、8相图 |
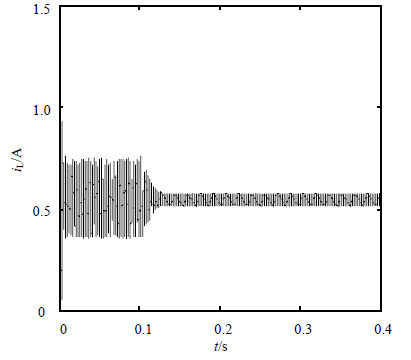 |
| 图8 电感电流由混沌状态过渡到周期1状态的过程,在$t=0.1\ \text{s}$时开始施加混合控制策略 |
 |
| 图9 控制后周期1电感电流波形(γ=0.6) |
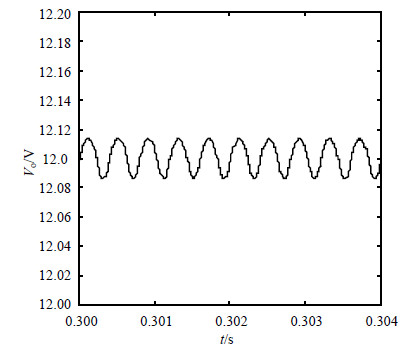 |
| 图10 控制后周期1输出电压波形(γ=0.6) |
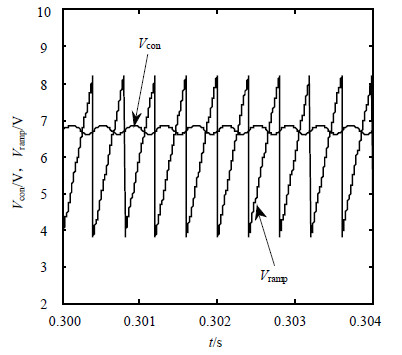 |
| 图11 控制后周期1开关逻辑图(γ=0.6) |
图 7a~图 7d分别表示控制后周期1、2、4、8的相图,它们由有限条闭合轨线组成。图 8描述了施加混合控制策略前后即t=0.1s前后,电感电流由混沌状态过渡到周期1状态的过程(γ=0.6)。同样,可得电感电流由混沌状态过渡到周期2、4、8状态的过程,及输出电压Vo和控制电压Vcon由混沌状态过渡到周期1、2、4、8状态的过程,因篇幅有限,这里不再给出。
控制后周期1电感电流波形如图 9所示、输出电压波形如图 10所示、开关逻辑图如图 11所示,可得一致的结果:它们的波形是规则、固定的。同样,可得控制后周期2、4、8电感电流波形、输出电压波形、开关逻辑图。
5 结论本文采用一种混合控制策略实现了电压控制型Buck变换器的混沌控制。结果表明,随着外部可调参数γ的减小,即$\gamma=0.6>0.15>0.08>0.065$,该策略能够将变换器的混沌状态控制在周期${{2}^{n}}$($n=0,1,2,3$)轨道上。该策略不需要预先确定期望的目标轨道,不依赖变换器的内部电路参数,其控制结果只与一个外部可调参数γ的大小有关,因而该策略也可用来控制其他电力电子电路中的混沌。
| [1] | OTT E, GREBOGI C, YORKE J A. Controlling chaos[J]. Physical Review Letters, 1990, 64(11): 1196-1199. |
| [2] | WANG Liang, XU Wei, LI Ying. Impulsive control of a class of vibro-impact systems[J]. Physics Letters A, 2008, 372: 5309-5313. |
| [3] | TAVAZOEI M S, HAERI M, JAFARI S, et al. Some applications of fractional calculus in suppression of chaotic oscillations[J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 4094-4101. |
| [4] | FALAHPOOR M, ATAEI M, KIYOUMARSI A. A chattering-free sliding mode control design for uncertain chaotic systems[J]. Chaos Solitons and Fractals, 2009, 42: 1755-1765. |
| [5] | LAOYE J A, VINCENT U E, KAREEM S O. Chaos control of 4D chaotic systems using recursive backstepping nonlinear controller[J]. Chaos Solitons and Fractals, 2009, 39: 356-362. |
| [6] | IU H H C, YU D S, FITCH A L, et al. Controlling chaos in a memristor based circuit using a twin-T notch filter[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2011, 58(6): 1337-1344. |
| [7] | ZHANG Zhen, CHAU K T, WANG Zheng. Analysis and stabilization of chaos in the electric-vehicle steering system[J]. IEEE Transactions on Vehicular Technology, 2013, 62(1): 118-126. |
| [8] | ZHUSUBALIYEV Z T, MOSEKILDE E, MAITY S, et al. Border collision route to quasiperiodicity: Numerical investigation and experimental confirmation[J]. Chaos, 2006, 16: 02312211-0231221. |
| [9] | MAITY S, TRIPATHY D, BHATTACHARYA T K, et al. Bifurcation analysis of PWM-1 voltage mode controlled Buck converter using the exact discrete model[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2007, 54(5): 1120-1130. |
| [10] | MIRANDA M, ALVAREZ J. Bifurcations and chaos produced by the modulation signal in a PWM buck converter[J]. Chaos Solitons and Fractals, 2009, 42: 2260-2271. |
| [11] | WOOD J R. Chaos: a real phenomenon in power elctronics[C]//Applied Power Electronics Conference and Exposition. Baltimore, MD, USA: IEEE, 1989: 115-124. |
| [12] | DEANE J H B, HAMILL D C. Instability, subharmonics, and chaos in power electronic systems[J]. IEEE Transactions on Power Electronics, 1990, 5(3): 260-268. |
| [13] | GUESMI K, HAMZAOUI A, ZAYTOON J. Control of nonlinear phenomena in DC-DC converters: Fuzzy logic approach[J]. International Journal of Circuit Theory and Applications, 2008, 36: 857-874. |
| [14] | MA W, WANG M Y, LI C. Control of bifurcation in the one-cycle controlled Cuk converter[J]. Nonlinear Dynamics, 2012, 67: 2573-2583. |
| [15] | 贾美美, 张国山, 牛弘. 基于改善关联性Buck变换器的混沌控制[J]. 物理学报, 2013, 62(13): 1305031-1305038. JIA Mei-mei, ZHANG Guo-shan, NIU Hong. Chaotic control of the buck converter based on improving the correlation[J]. Acta Physica Sinica, 2013, 62(13): 1305031-1305038. |
| [16] | ZHOU Y F, TSE C K, QIU S S, et al. Applying resonant parametric perturbation to control chaos in the buck DC-DC converter with phase shift and frequency mismatch considerations[J]. International Journal of Bifurcation and Chaos, 2003, 13(11): 3459-3471. |
| [17] | ZHOU Y F, TSE C K, QIU S S, et al. An improved resonant parametric perturbation for chaos control with applications to control of DC-DC converters[J]. Chinese Physics, 2005, 14(1): 61-66. |
| [18] | NATSHEH A N, KETTLEBOROUGH J G, JANSON N B. Experimental study of controlling chaos in a DC-DC boost converter[J]. Chaos Solitons and Fractals, 2009, 40: 2500-2508. |
| [19] | 卢伟国, 周雒维, 罗全明. 电压模式Buck变换器输出延迟反馈混沌控制[J]. 物理学报, 2007, 56(10): 5648-5654. LU Wei-guo, ZHOU Luo-wei, LUO Quan-ming. Output time-delay feedback control of chaos in voltage-mode Buck converter[J]. Acta Physica Sinica, 2007, 56(10): 5648-5654. |
| [20] | PODDAR G, CHAKRABARTY K, BANERJEE S. Control of chaos in the Boost converter[J]. Electronics Letters, 1995, 31(11): 841-842. |
| [21] | CHAKRABARTY K, BANERJEE S. Control of chaos in piecewise linear systems with switching nonlinearity[J]. Physics Letters A, 1995, 200(2): 115-120. |
| [22] | DAI D, TSE C K, MA X K. Symbolic analysis of switching systems: Application to bifurcation analysis of DC-DC switching converters[J]. IEEE Transactions on Circuits and Systems-I: Regular Papers, 2005, 52(8): 1632-1643. |
| [23] | HAMILL D C, DEANE J H B, JEFFERIES D J. Modeling of chaotic DC-DC converters by iterated nonlinear mappings[J]. IEEE Transactions on Power Electronics, 1992, 7(1): 25-36. |
| [24] | GIAOURIS D, MAITY S, BANERJEE S, et al. Application of filippov method for the analysis of subharmonic instability in DC-DC converters[J]. International Journal of Circuit Theory and Applications, 2009, 37(8): 899-919. |
| [25] | 钟洁, 于盛林. 电路参数变化引起的DC-DC变换器混沌现象的仿真研究[J]. 吉林大学学报(工学版), 2003, 33(4): 73-78. ZHONG Jie, YU Sheng-lin. Simulation study on chaos in DC-DC converter depending on variation of circuit parameters values[J]. Journal of Jilin University (Engineering and Technology Edition), 2003, 33(4): 73-78. |
| [26] | LU W G, ZHOU L W, LUO Q M. Notch filter feedback controlled chaos in Buck converter[J]. Chinese Physics, 2007, 16(11): 3256-3261. |
| [27] | LU W G, ZHOU L W, WU J K. Self-stable chaos control of DC-DC converter[J]. Chinese Physics Letters, 2009, 26(3): 0305031-0305034. |
| [28] | LUO X S, Chen G R, Wang B H, et al. Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems[J]. Chaos, Solitons and Fractals, 2003, 18: 775-783. |
 2016, Vol. 45
2016, Vol. 45
