目标跟踪是无线传感器网络(wireless sensor networks,WSN)的典型应用之一,多目标跟踪的目的是确定目标的位置、身份以及运动状态等融合信息,涉及到WSN中的路由、定位、加密以及数据融合等关键技术[1,2,3,4]。在实际应用环境中,目标节点会受到多个因素的影响,机动性和隐蔽性都在不断地增强,因而新形势下的多目标跟踪问题会变得越来越复杂。如何在复杂环境中实现快速定位和跟踪多目标的动态轨迹成了研究的重点[5,6,7,8]。
WSN多目标跟踪的方法有很多,目前的讨论热点是如何在系统跟踪精度与网络能量开销之间做一个权衡关系,要求在尽量提高系统跟踪精度的同时,也能有效节省节点的能量开销,从而延长网络的生命周期[9,10]。比如在跟踪算法中加入节点的唤醒机制,处在监控区域中的传感节点均处于一种周期性的睡眠状态,只有当节点检测到有事件发生时,才会通过事件触发的方式唤醒自己进行事件的跟踪与监控,有效地减少了节点的能量开销。同时,基于区域查询的跟踪应用也越来越受到关注与重视。用户指定任意一片监控区域,可以对该区域中目标的个数、身份及状态等信息进行查询访问。但现有的区域查询算法能耗开销大,查询时延长,且能同时对目标进行区域查询以及轨迹跟踪的研究较少。
针对以上问题,本文提出了一种新的基于边权值动态轨迹的多目标区域跟踪算法EWDT。主要处理流程如下:
1)构建系统模型,采用节点唤醒机制来有效降低系统的能耗开销,延长网络周期;
2)采用网络分割算法进行网络平面划分,并赋予网络中每条划分边初始权值。实时更新边权值,当权重为w的监测目标进入某个区域顺时针跨过一条边时,该边的权值会自增w。反之离开某块区域,逆时针跨过一条边时,该边的权值则自减w;
3)设计节点边权值状态转换策略和查询统计机制,完成节点间状态转换和区域有效查询;
4)采用卡尔曼滤波技术设计轨迹跟踪算法,实现动态跟踪目标,确定目标当前的位置或者预测下一个时刻目标的位置。
1 相关研究目标跟踪在国内外已有较多的研究。文献[9]提出了一种可以用于处理多种跟踪问题的近似最优方法—卡尔曼(KALMAN)滤波,该算法通过对含有噪声数据的测量值进行递归性的融合,从而得出系统状态的较为准确的估计。该算法具有较强的跟踪精度,但只用于单目标跟踪中,且系统所需的计算开销较大。
文献[10]提出了一种基于树形的目标跟踪算法(scalable tracking using networked sensors,STUN),用以对网络中的移动目标进行跟踪和监控。该算法的实现非常简单,路由结构也较为稳定,节点的计算存储开销都较小。但需要网络中的所有节点都一直处于工作状态,能耗较大,跟踪精度也不高。
文献[11]对STUN算法进行了改进,提出了一种新的目标跟踪算法(dynamicconvoy tree based collaboration,DCTC)[11]。该算法的基本思想是在监控目标的周围建立一棵用于目标跟踪的传送树,树内节点的动作由树根节点进行决策。DCTC算法通过建立传送树的机制,有效地节省了网络中的能量消耗。但是基于树状的网络结构,系统的可扩展性受到了限制。
文献[12]提出了一种基于簇状网络结构的算法(dynamic cluster detection and tracking,DCDT)。该算法以检测目标信息的所有网络节点组成边界节点构建动态跟踪簇,而处于边界处的节点可能会被划分到多个簇里面。DCDT算法具有较高的跟踪精度,系统的实时性也比较强,通常情况下可以有效地降低系统的计算以及通信开销。但当网络中目标的运动轨迹频繁出现交叉相遇时,系统便会频繁地进行动态跟踪簇的合成与分解,这势必会给系统造成严重的资源开销,影响系统的性能。
文献[13]提出了一种区域跟踪算法(continuous objects tracking algorithm,COTA)。COTA算法是以一片连续的区域作为监测目标,该目标具有覆盖范围广、随机性强、受环境因素影响大等特点,相比大多数传统的目标跟踪算法,该算法是一种较新型的算法,具有较强的实时性和稳定性,所需的能量开销较小。不过该算法是以火情监控、化学气体泄露、放射性物质辐射等为应用场景,这就需要对节点进行更好的物理保护,并且所涉及到的节点数量众多,这可能会造成系统成本的增加。
文献[14]提出的LLS算法将网络划分为网格结构,网络中若干节点作为中心节点,中心节点周围的邻居节点作为其附属节点。当目标进入某块监控区域时,附属节点负责采集目标信息,而中心节点只负责信息的处理。总体上跟踪精度较高,但该算法要求中心节点具有较强的处理能力,实际应用性不强,且算法的计算开销也较大。
文献[15]提出Forms算法,通过对任意指定的一块区域进行边权值计算,可以对该区域中目标的个数、身份以及状态等关键信息进行分析和确认,能够进行区域查询。但该算法边权值更新过程能耗过大,无法对目标进行轨迹跟踪。
综上分析,现有的多目标跟踪算法虽然都取得了一定的效果,同时也存在着通信和计算开销大、平均更新和查询时间长等缺点。
2 系统构建模型 2.1 传感模型1)节点模型:在传感器节点中,其功能模块与通讯模块之间相互独立,功能模块主要负责环境信息的采集,而通信模块主要用于数据的转发与传送,并且节点采集一次数据所消耗的能量远远大于节点进行一次信道侦听所消耗的能量。
2)节点唤醒机制:处在监控区域中的传感节点都处于一种周期性的睡眠状态,在这种周期性的睡眠状态下,节点的通讯模块以时间${T_1}$作为周期进行信道侦听,当接收到其邻居节点发送的特定信息时,将会唤醒自己的功能模块,并以时间${T_2}$为周期进行数据采集,当检测到有事件发生时再进入唤醒状态,并开始对目标事件进行监控跟踪。其中${T_2}=N{T_1}$,这样既可以保证网络中的节点在没有事件发生时能量消耗降到最低,也可以保证当节点采集到数据需要向周围节点发送信息时,节点的通讯模块也正好是开启的。
2.2 网络模型在该方案中,网络模型有如下假设:网络中的所有节点间彼此同构对等,且随机分布,节点部署后的坐标位置均已知。单个节点对环境的监测范围等于其通信半径R。系统中监测目标根据各自的不同特征赋予不同的权重值,第i个目标的权值为wi。对于算法中将要使用到的常量定义如下:
传感节点部署的区域为B,节点集合为V,其中$V=\{ {v_i}\},i=1,2,\cdots,N$,N表示节点数目,节点vi的监测区域Bi是以节点为圆心、R为半径的圆,因此$B={B_1} \cup {B_2} \cup \cdots \cup {B_N}$。
3 EWDT算法的设计以下从系统初始化、边权值更新、节点间的状态转换、区域查询以及轨迹跟踪这5个步骤详细描述算法设计。
3.1 系统初始化节点采用随机部署的方式,并根据网络分割算法[16,17]将网络进行平面划分,得到一个网络节点的连通子图如图 1所示。图中,每个顶点表示一个节点,边表示节点间可以单跳通信,所有边初始权重值为0。
 |
| 图1 节点初始化 |
在最初部署系统时,所有的网络节点都处于周期性的睡眠状态。假设在某时刻发生了突发事件,这时事件周围的某些节点必然会检测到该目标信息,并且会修改自身所对应边的权重值。这些节点将进入唤醒状态,向其周围邻居节点传播唤醒消息,记为W_Message,消息的具体格式如表 1所示。
| 表1 W_Message格式 |
接收到唤醒消息的节点以及最初检测到目标信息的节点此后都会周期性地检测其通信范围内多边形边的权重值,若权重值为0,则节点继续保持等待状态,并同时启动一个定时器,这时可以分为两种情况:
1)若在定时器设定的时间内边权重值始终为0,则节点进入睡眠状态;
2)若在定时器设定的时间内边权重值不为0,则说明有目标在该节点的检测范围之内,此时节点开启功能模块对目标进行周期性的信息采集。
3.2 边权值的更新边权值更新流程如图 2所示。每一块区域都能表示成若干条有向边的顺时针连接,如图中的区域ABD、BCD以及ABCD。方向相反的两条边的权值互为相反数,如边AB的权值为x,则边BA的权值为-x。区域的权值统计结果为顺时针方向组成该区域的各边权值之和,W(ABCD)=W(AB)+W(BC)+W(CD)+W(DA)。假设当权值为w的监控目标跨过一条边进入某块区域时,该边的权值会相应的增加w,相反当目标跨过一条边离开某块区域时该边的权值会减少w。
 |
| 图2 边权值更新 |
图中,权值为w的监控目标由区域ABD跨过边BD进入区域BCD时,边BD的权重值会自加w,而边DB的权重值会自减w,即W(ABD)-=w,W(BCD)+=w,然而W(ABCD)=W(ABD)+W(BCD)结果保持不变,因为此时目标仍处于区域ABCD中。
3.3 节点间的状态转换1)休眠节点的状态转换
处于休眠状态的节点接收到W_Message消息后,将进入等待状态,所有处于等待状态的节点${v_i}$都将以${T_s}$为周期,对自己的检测区域${B_i}$进行边权重值的统计,根据检测的结果不同,分为以下两种情况:
①区域统计的权值和不为0,则节点进入检测状态,对目标进行信息采集,并且向其周围节点发送唤醒消息。
②区域统计的权值和在一段时间内始终都为0,则进入睡眠状态。
2)唤醒状态节点的状态转换
处于唤醒状态的节点${v_i}$需以时间${T_s}$为周期对区域${B_i}$进行目标的信息采集,同时对区域${B_i}$进行边的权值计算,根据计算结果的不同,节点分为以下两种情况:
①若节点${v_i}$对区域${B_i}$权值统计不为0,则${v_i}$会向其周围节点传播W_Message消息。而对于那些已经处于检测状态的节点接收到W_Message时,则直接丢弃;
②若节点${v_i}$在${T_0}$$时刻检测到权值为0,则节点立刻进入等待状态,并启动一个定时器,在一段时间内若统计到权值不为0则进入检测状态,否则进入睡眠状态。节点间的状态转移图如图 3所示。
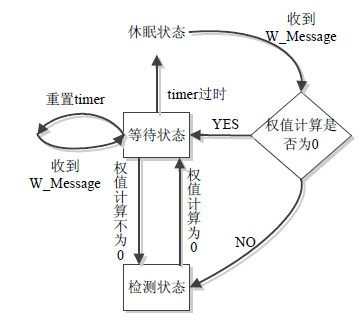 |
| 图3 节点状态转移图 |
由于系统初始化过程中,所有边的权重值都初始化为0,并且当目标进入一块区域后再离开该区域时不会造成区域权值的变化。所以可以通过对指定的一块区域进行边权值的统计判断其结果是否为0,若为0则说明该区域中不存在监控目标,否则说明该区域存在有监控目标。在特定情况下还能对该区域中的目标个数以及身份信息进行确认。
区域查询如图 4所示,每个监控目标事先都根据其不同的重要特性按照2的幂次赋初始权值,对区域ABCD进行查询:各边权重值相加为W(ABCD)=4+0+0+2=6,由此可以判断该区域中含有权重值为2和4的两个监控目标。对区域CEFD进行查询:W(CEFD)=0+1+0+0,由此可见该区域中只含有权重值为1的监控目标。对区域ADG进行查询:由于W(DA)=2,则W(AD)=2,说明该区域中不含监控目标。
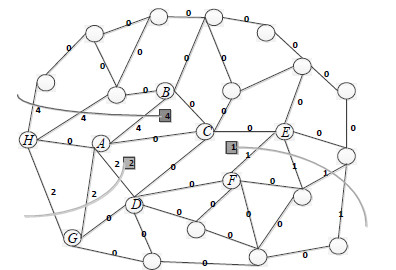 |
| 图4 区域查询 |
在边权值的基础上结合动态跟踪簇以及卡尔曼滤波技术,除了可以对区域进行目标查询外,还能对目标进行传统的轨迹跟踪。轨迹跟踪如图 5所示。普通节点将目标的监控信息发送给簇头节点,簇头节点对收集的信息进行滤波处理,以确定目标当前的位置或者预测下一时刻目标出现的位置。
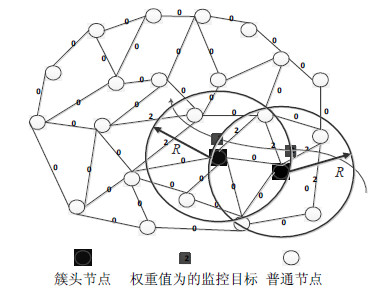 |
| 图5 轨迹跟踪 |
假设${\bf{X}}(k)$是系统的状态向量,${\bf{Z}}(k)$是系统状态的观测向量,${\bf{\Phi }}(k+1,k)$是系统的状态转移矩阵,${\bf{V}}(k)$是系统观测的噪声向量,${\bf{W}}(k)$是系统状态的随机干扰向量,${\bf{H}}(k)$是系统的观测矩阵。则系统的状态方程和观测方程可表示为:
| ${\bf{X}}(k+1)={\bf{\Phi }}(k+1,k){\bf{X}}(k)+{\bf{W}}(k)$ | (1) |
| ${\bf{Z}}(k)={\bf{H}}(k){\bf{X}}(k)+{\bf{V}}(k)$ | (2) |
首先通过卡尔曼滤波估计每个监控目标在下一个时刻点t的位置,并利用式(3)对估计的位置信息与最新获得的位置信息之间的相关性进行测量,以便得到一组相关概率值$\{ P({t_1},T),P({t_2},T),\cdots,P({t_n},T)\} $。然后找出其中的最大概率值${P_{\max }}$,并将${P_{\max }}$与门限值P进行比较,若${P_{\max }} \ge P$则说明当前观测值与${P_{\max }}$所对应的轨迹具有相关性,否则说明当前观测值与所有轨迹都不具有相关性,即当前观测信息是一个新目标加入网络时所测得的。可以将对多个目标进行跟踪的问题转化为一组单目标跟踪的问题。
假设用监控目标的位置、速度以及加速度来表示其在每个时刻的状态。而在目标跟踪的整个过程中,节点的采样周期很小,所以在一个周期内目标的运动近似为匀速运动。在此定义卡尔曼滤波器的系统状态为:
| ${x_k}={[{x_{ik}},{y_{ik}},{v_{xk}},{v_{yk}},{a_{xk}},{a_{yk}}]^{\mathop{\rm T}\nolimits} }$ | (3) |
式中,${x_{ik}}$、${y_{ik}}$为目标${T_i}$的坐标位置;${v_{xk}}$、${v_{yk}}$为目标在第k个时刻时的x轴方向和y轴方向的速度;${a_{xk}}$、${a_{yk}}$为目标在第k个时刻时的x轴方向和y轴方向的加速度,状态方程为:
| ${X_k}={\bf{\Phi }}{x_{k - 1}}+{K_k}[{Z_k} - H{\bf{\Phi }}{X_{k - 1}}]$ | (4) |
式中,${X_{k - 1}}$为目标第$k - 1$个时刻状态的卡尔曼滤波输出;${X_k}$为目标在第k个时刻状态的卡尔曼滤波输出;${Z_k}$为第k个时刻的观测状态;${K_k}$为第k个时刻的卡尔曼滤波系数;${\bf{\Phi }}$为第$k - 1$个时刻到第k个时刻的状态转移矩阵。假设目标在一个周期内是匀速运动的,${\bf{\Phi }}$可定义为:
| ${\bf{\Phi }}=\left[ {\begin{array}{*{20}{c}} 1&0&{\Delta t}&0&{{{(\Delta t)}^2}/2}&0\\ 0&1&0&{\Delta t}&0&{{{(\Delta t)}^2}/2}\\ 0&0&1&0&{\Delta t}&0\\ 0&0&0&1&0&{\Delta t}\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right]$ | (5) |
EWDT轨迹跟踪算法流程为:
输入:在第k个时刻获取的观测值${Z_k} $
输出:预测的轨迹
步骤1:
//计算${Z_1},{Z_2},\cdots,{Z_{k - 1}}$对${Z_k}$的预测值${Z'_k} $
//以及预测值与测量值之间的相关度
FOR i=1:1:n
${D_{nk}}=P({Z_k},{Z'_k})$
END FOR
步骤2:
//选择相关概率最大的轨迹进行关联
${D_t}=\max({D_{nk}})$
步骤3:
计算轨迹t的${K_k}$
步骤4:
计算轨迹t的${P_k}$和${P_{k+1}} $
步骤5:
更新轨迹t的卡尔曼滤波器
步骤6:
FINISH()//结束计算
4 实验及性能评估从边权值更新和目标查询两个过程中的平均能耗与时延方面,对本文提出的EWDT算法、Forms算法以及LLS算法进行性能分析与比较。
4.1 实验参数设置具体实验参数如表 3所示:
| 表3 实验参数 |
图 6和图 7分别表示系统的平均查询时间和查询时的平均能量消耗,当网络节点规模从1000逐渐增加到10000时,网络规模越大则查询区域离监控中心的平均距离也越大,所以系统的平均查询时间和查询时的平均能量消耗也会显著的增加。
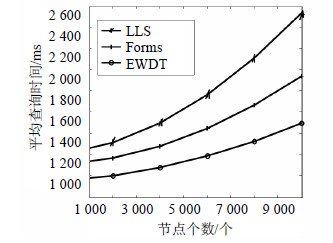 |
| 图6 平均查询时间 |
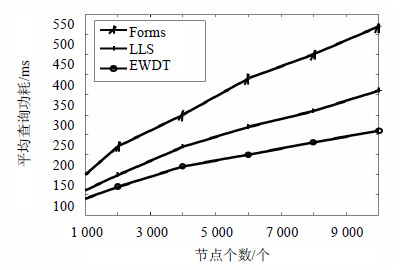 |
| 图7 平均查询能耗 |
由于在EWDT算法中采用了动态跟踪簇对目标进行跟踪,对于普通区域的查询无需进行边权值的统计,而只需对包含在跟踪簇里的查询区域进行权值统计,相比较Forms和LLS而言,EWDT算法能在较大程度上减少系统查询时的处理开销以及处理时延。通过计算比较分析后可知,在系统平均查询时间上,EWDT算法相对于Forms算法以及LLS算法分别减少了21.8%和36.4%的查询时间;而在系统平均查询能耗上则分别减少了18.6%和30.5%。
4.3 平均更新时间与能耗图 8和图 9分别表示系统平均更新时间以及更新过程中的平均能量开销。
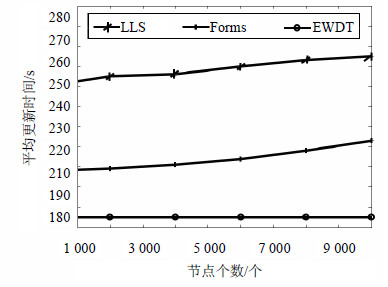 |
| 图8 平均更新时间 |
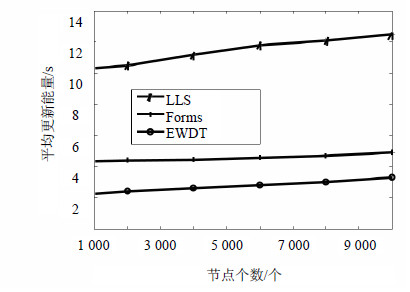 |
| 图9 平均更新能量 |
虽然网络规模逐渐增大,但并不影响系统在局部区域进行边权值更新时的平均能量开销以及平均处理时延,因此几乎不受网络规模大小的影响。但在EWDT算法中加入了节点状态转换机制,并通过统计节点所在区域的边权值是否为0这种最简单的方式来进行节点的状态转换,从而大大的减少了节点采样信息的频率。因此相比Forms算法和LLS算法,在相同的网络规模时EWDT算法可以在较大程度上减少系统的平均更新成本以及更新时延。通过比较分析可知,在系统更新上,EWDT算法相对于Forms算法以及LLS算法分别减少了12.3%和30.2%的更新时间;而在系统平均更新能耗上则分别减少了50.4%和78.6%。
5 结束语通过实验对比结果分析可知,EWDT算法在区域查询和边权值更新过程中,系统平均能耗和平均时延都能大大的减小,从而延长了网络周期,增强了系统的实用性。
| [1] | QU H, HOU G, GUO Y, et al. Localization with single stationary anchor for mobile node in wireless sensor networks[J]. International Journal of Distributed Sensor Networks, 2013(1): 74-82. |
| [2] | 王瑞锦, 秦志光, 包红来, 等. 基于三角划分的复杂3D凹/凸不平表面网络定位算法[J]. 计算机应用研究, 2013, 30(9): 2823-2830. WANG Rui-jin, QIN Zhi-guang, BAO Hong-lai, et al. Triangulation-based localization algorithm over complex 3D terrains[J]. Application Research of Computer, 2013, 30(9): 2823-2830. |
| [3] | 王瑞锦, 秦志光, 王佳昊. 无线传感器网络分簇路由协议分析[J]. 电子科技大学学报, 2013, 42(3): 400-406. WANG Rui-jin, QIN Zhi-guang, WANG Jia-hao. Analysis of wireless sensor network cluter routing protocol[J]. Journal of University of Electronic Science and Technology of China, 2013, 42(3): 400-406. |
| [4] | ZHOU H, WU H, JIN M. A robust boundary detection algorithm based on connectivity only for 3D wireless sensor networks[C]//2012 Proceedings IEEE on International Conference on Computer Communications. Orlando, USA: IEEE, 2012. |
| [5] | WANG R J, BAO H L, CHEN D J, et al. 3D-CCD: a novel 3D localization algorithm based on concave/convex decomposition and layering scheme in WSNs[J]. Ad hoc & Sensor Wireless Networks, 2014(23): 235-254. |
| [6] | WANG J, HUANG L, LI X, et al. A collaborative localization scheme from connectivity in wireless sensor networks[C]//Wired/Wireless Internet Communications. Finland: Springer, 2008: 213-223. |
| [7] | WANG R J, QIN Z G. A weighted 3D localization algorithm based on partial hop size in wireless sensor network[J]. International Journal of Advancementsin Computing Technology, 2012, 4(9): 504-513. |
| [8] | WANG R J, QIN Z G, LI D F, et al. 3DT-PP: Localization and path planning of mobile anchors over complex 3D terrains[J]. High Technology Letters, 2014(4): 367-375. |
| [9] | SHENG X, HU Y H, RAMANATHAN P. Distributed particle filter with GMM approximation for multiple targets localization and tracking in wireless sensor network[C]//.Proceedings of the 4th International Symposium on Information Processing in Sensor Networks. [S.l]: IEEE, 2005. |
| [10] | 王瑞锦. 复杂环境下的无线传感器网络定位关键技术研究[D]. 成都: 电子科技大学, 2013. WANG Rui-jin. Key techniques of localization in wireless sensor networks under complex environment[D]. Chengdu: University of Electronic Science and Technology of China, 2013. |
| [11] | ZHANG W, CAO G. DCTC: Dynamic convoy tree-based collaboration for target tracking in sensor networks[J]. IEEE Transactions on Wireless Communications, 2004, 3(5): 1689-1701. |
| [12] | JI X, ZHA H, METZNER J J, et al. Dynamic cluster structure for object detection and tracking in wireless ad-hoc sensor networks[C]//IEEE International Conference on Communications. [S.l.]: IEEE, 2004, 7: 3807-3811. |
| [13] | 鲍微. 无线传感器网络中能量高效的目标跟踪问题研究[D]. 合肥: 中国科学技术大学, 2009. BAO Wei. Research on energy-efficient target tracking in WSNs[D]. Hefei: University of Science and Technology of China, 2009. |
| [14] | ABRAHAM I, DOLEV D, MALKHI D. LLS: a locality aware location service for mobile Ad hoc networks[C]//Proceedings of the 2004 Joint Workshop on Foundations of Mobile Computing. [S.l.]: ACM, 2004. |
| [15] | SARKAR R, GAO J. Differential forms for target tracking and aggregate queries in distributed networks[J]. IEEE/ACM Transactions on Networking, 2013, 21(4): 1159-1172. |
| [16] | SARKAR R, YIN X, GAO J, et al. Greedy routing with guaranteed delivery using ricci flows[C]//International Conference on Information Processing in Sensor Networks, IPSN 2009. [S.l.]: IEEE, 2009: 121-132. |
 2016, Vol. 45
2016, Vol. 45
