随着无线局域网(WLAN)的广泛部署,利用WLAN基础设施进行定位可以大大降低定位设备和系统维护的开销。目前,基于RSS的室内WLAN位置指纹定位系统得到了广泛的关注[1, 2, 3]。该系统主要包括两个阶段,即离线阶段和在线阶段。在离线阶段,系统需在定位目标区域内选择一定数目的参考点(reference point,RP),并在每个参考点处测量来自不同接入点(access point,AP)的信号强度值,建立位置指纹数据库;在在线阶段,通过用户实测RSS值与位置指纹数据库中的指纹数据进行匹配,从而实现对用户的定位。
位置指纹定位方法需在离线阶段采集所选RP处来自不同AP的信号强度值,从而需要大量的人力和时间开销。为了解决这一问题,人们提出了基于即时定位与SLAM的室内WLAN定位方法[4, 5]。然而,由于SLAM定位方法需要利用传感器信息进行辅助定位,所以其对终端设备的选择会有特殊的要求。同时,考虑到在大多数基于位置的服务(location based services,LBS)中,往往勿需精确计算用户的位置坐标,而仅需获得用户所处的位置区域或其周边的位置信息。基于此,本文提出了一种基于图像边缘检测的WLAN室内用户运动地图构建及映射方法,首先在定位目标区域内随机采集一定数目的RSS序列;然后,利用谱聚类算法对带有时间戳标记的RSS序列进行聚类处理,以构建RSS类转移图;其次,利用图像边缘检测方法,对得到的RSS类转移图进行拼接,以建立运动用户所对应的信号空间逻辑图;最后,根据信号空间逻辑图与定位目标区域的物理连接图的映射关系,完成对用户位置的估计。此外,采用绘图正交算法对逻辑图与物理连接图进行绘制,以增强图形结构的可读性和可靠性。
1 基于图像边缘检测的WLAN室内用户运动地图构建与映射 1.1 信号采集定义移动终端在定位目标区域内随机采集的z条接收信号的强度序列为${S_j} = \{ {\rm{RS}}{{\rm{S}}_{j{\rm{1}}}},{\rm{RS}}{{\rm{S}}_{j2}}, \cdots ,{\rm{RS}}{{\rm{S}}_{j{M_j}}}\} $(j=1,2,…,z),其中,Sj为第j条RSS序列,Mj为第j条接收信号强度序列的长度,即接收信号强度矢量个数,${\rm{RS}}{{\rm{S}}_{jk}} = ({\rm{RS}}{{\rm{S}}_{jk1}},{\rm{RS}}{{\rm{S}}_{jk2}}, \cdots ,{\rm{RS}}{{\rm{S}}_{jkn}})$,$k = (1,2, \cdots ,{M_j})$为第j条接收信号序列中第k个RSS矢量,n为AP个数,${\rm{RS}}{{\rm{S}}_{{\rm{jkr}}}}(r = (1,2, \cdots ,n))$为第j条接收信号强度序列中第k个RSS矢量内来自第r个AP的信号强度值。
在完成对接收信号强度序列的采集后,将各序列中的RSS矢量按升序标记时间戳。对于每个接收信号强度矢量中的时间戳和RSS进行加权,构成混合矢量${\varphi _{jk}} = ({w_{ts}}k,{w_{rss}}{\rm{RS}}{{\rm{S}}_{jk1}}, \cdots ,{w_{rss}}{\rm{RS}}{{\rm{S}}_{jkn}})$,其中,φjk为第j条接收信号强度序列中第k个混合矢量,wts和wrss分别为时间戳和RSS的权重,且wts+wrss=1。
1.2 逻辑图构建对每一条包含混合矢量的接收信号强度序列进行谱聚类[6],以得到每个混合矢量所属的聚类号及相应聚类的类心,然后利用中值滤波对序列中不同混合矢量所属的聚类号进行平滑处理,并根据相邻聚类的转移关系,以连接图的形式构建每条序列所对应的RSS类转移图,其中,中值滤波后的类号重排过程,其目的是得到较为规整的类号转移关系。
当得到所有RSS类转移图后,将利用图像边缘检测技术,确定不同RSS类转移图中不同聚类之间的相关性,同时合并相关性大于门限Std的RSS聚类,以实现对不同RSS类转移图的拼接,从而得到所有待筛选的信号逻辑图。具体步骤为:
1) 将所有接收信号强度序列按序号升序排列为$\Gamma = \{ {\rm{RS}}{{\rm{S}}_{11}},{\rm{RS}}{{\rm{S}}_{12}}, \cdots ,{\rm{RS}}{{\rm{S}}_{1{M_1}}},{\rm{RS}}{{\rm{S}}_{21}},{\rm{RS}}{{\rm{S}}_{22}}, \cdots ,{\rm{RS}}{{\rm{S}}_{2{M_2}}},{\rm{RS}}{{\rm{S}}_{z1}},{\rm{RS}}{{\rm{S}}_{z2}}, \cdots ,{\rm{RS}}{{\rm{S}}_{z{M_z}}}\} $。
2) 计算Γ中不同接收信号强度矢量的欧式距离,得到距离矩阵Mdis,其中,Mdis表示为:
| ${{\bf{M}}_{{\rm{dis}}}} = \left[ {\begin{array}{*{20}{c}} {d{i_{11}}}&{d{i_{12}}}&{...}&{d{i_{1{M_\Gamma }}}}\\ {d{i_{21}}}&{d{i_{22}}}&{...}&{d{i_{2{M_\Gamma }}}}\\ \vdots & \vdots & \ddots & \vdots \\ {d{i_{{M_\Gamma }1}}}&{d{i_{{M_\Gamma }2}}}&{...}&{d{i_{{M_\Gamma }{M_\Gamma }}}} \end{array}} \right]$ | (1) |
式中,MΓ为序列Γ中接收信号强度矢量个数;didi1di2 (di1,di2=1,2,…,MΓ)为序列Γ中第di1和第di2个接收信号强度矢量的欧氏距离,即相关性度量值。
3) 设定门限Std,当didi1di2<Std时,令didi1di2=1;当didi1di2≥Std时,令didi1di2=0。
4) 由于矩阵Mdis中每个元素刻画了序列Γ中对应接收信号强度矢量的相关性。对Mdis做中值滤波处理,可有效剔除矩阵中的奇异值元素,即减小环境噪声的影响。图 1为对原始矩阵进行中值滤波后所得的二值图像。
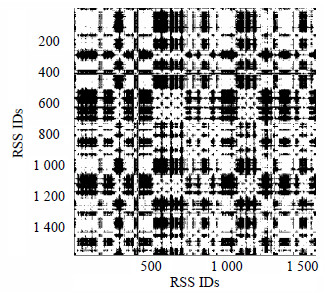 |
| 图1 中值滤波处理后的二值图像 |
此外,对图 1中的二值图像进行腐蚀处理,能够得到矩阵中数值为1的元素块,即相关性较大的元素集合。由于矩阵中(xpi,ypi)(xpi,ypi=1,2,…,MΓ)处的元素值表示序列Γ中第xpi个和第ypi个接收信号强度的相关性,故相关性较大的元素集合能够有效表征序列Γ中相关性较强的接收信号强度序列。图 2为经腐蚀处理后的二值图像。
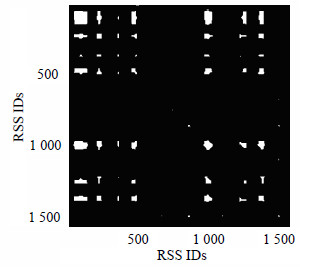 |
| 图2 腐蚀处理后的二值图像 |
5) 选定二值图像中横向和纵向边缘检测Sobel卷积因子Gx和Gy,并用3×3的滑动窗遍历腐蚀图像中的元素,得到腐蚀图像中第dis_a行且第dis_b列的元素,Ero(dis_a,dis_b)(dis_a,dis_b=1,2,…,MΓ),在横向和纵向的灰度差分值Gx_dis_a和Gy_dis_a,其中,Gx和Gy分别为:
| ${{\bf{G}}_x} = \left[ {\begin{array}{*{20}{c}} { + 1}&{ + 2}&{ + 1}\\ 0&0&0\\ { - 1}&{ - 2}&{ - 1} \end{array}} \right],{\rm{ }}{{\bf{G}}_y} = \left[ {\begin{array}{*{20}{c}} { - 1}&0&{ + 1}\\ { - 2}&0&{ + 2}\\ { - 1}&0&{ + 1} \end{array}} \right]$ | (2) |
此外,Gx_dis_a和Gy_dis_a分别为:
| $\begin{array}{c} {{\bf{G}}_{x\_{\rm{dis}}\_a}} = {\rm{Ero}}(({\rm{dis}}\_a) + 1,({\rm{dis}}\_b) + 1) + \\ 2{\rm{Ero}}(({\rm{dis}}\_a),({\rm{dis}}\_b) + 1) + \\ {\rm{Ero}}(({\rm{dis}}\_a) - 1,({\rm{dis}}\_b) + 1) - \\ [{\rm{Ero}}(({\rm{dis}}\_a) + 1,({\rm{dis}}\_b) - 1) + \\ 2{\rm{Ero}}(({\rm{dis}}\_a),({\rm{dis}}\_b) - 1) + \\ {\rm{Ero}}(({\rm{dis}}\_a) - 1,({\rm{dis}}\_b) - 1)]\\ {{\bf{G}}_{y\_{\rm{dis}}\_b}} = {\rm{Ero}}(({\rm{dis}}\_a) + 1,({\rm{dis}}\_b) + 1) + \\ 2{\rm{Ero}}(({\rm{dis}}\_a) + 1,({\rm{dis}}\_b)) + \\ {\rm{Ero}}(({\rm{dis}}\_a) + 1,({\rm{dis}}\_b) - 1) - \\ [{\rm{Ero}}(({\rm{dis}}\_a) - 1,({\rm{dis}}\_b) + 1) + \\ 2{\rm{Ero}}(({\rm{dis}}\_a) - 1,({\rm{dis}}\_b)) + \\ {\rm{Ero}}(({\rm{dis}}\_a) - 1,({\rm{dis}}\_b) - 1)] \end{array}$ | (3) |
由Gx_dis_a和Gy_dis_a,可利用式(4)计算得到元素Ero(dis_a,dis_b)的灰度差分值Gxy,即:
| ${G_{xy}} = |{{\bf{G}}_{x\_{\rm{dis}}\_a}}| + |{{\bf{G}}_{y\_{\rm{dis}}\_b}}|$ | (4) |
设定灰度差分门限Gth,当Gxy≥Gth时,令Ero(dis_a,dis_b)=1,当Gxy<Gth时,令Ero(dis_a,dis_b)=0。图 3为经腐蚀处理后的某局部图像,图 4为图 3经边缘检测后所得到的图像。从图 4可以看出,经边缘检测后所得图像,将原始矩阵中相关性较大的元素块的边缘轮廓信息进行了提取,根据轮廓的长度和宽度可得对应的接收信号强度矢量序号。
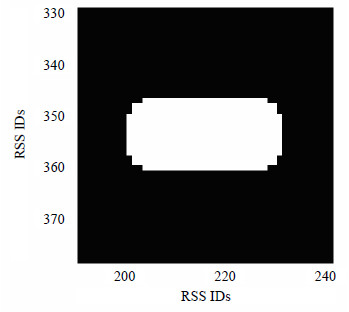 |
| 图3 腐蚀处理后的某局部图像 |
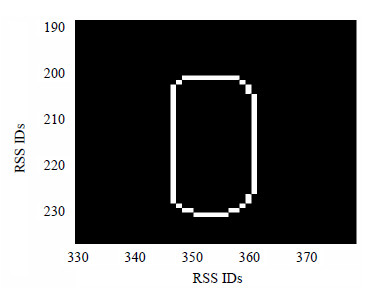 |
| 图4 边缘检测后的某局部图像 |
在将腐蚀后的图像经边缘检测后,可得序列Γ中所有相关性较大的接收信号强度矢量的序号。此外,根据RSS类转移图构建中的谱聚类结果,可知每个接收信号强度矢量的所属聚类,从而,利用Γ中所有相关性较大的接收信号强度矢量的序号信息,可得Γ中相关性较大的RSS聚类。将相关性较大的RSS聚类进行合并,用合并前各RSS聚类的类心均值作为合并后的新的类心,且保持合并前后各类之间的连接关系。最后,将此拼接后的逻辑图与剩余未拼接的逻辑图共同构成待筛选的逻辑图。
6) 以定位目标区域内的每个物理交叉路口作为区域边界进行子区域划分,并对每个子区域进行序号标记。此外,在定位目标区域内随机选择少量标记位置点(calibration point,CP),且在各标记位置点处采集少量来自不同AP的信号强度值,并将其均值矢量作为各标记位置点的代表矢量(representative vector,RV)。
7) 计算得到与每个RV具有最小欧式距离的信号逻辑图中的节点(或称逻辑节点),且令此逻辑节点与该RV所对应子区域存在映射关系。同时,剔除包含与不止一个子区域存在映射关系的逻辑节点的待筛选信号逻辑图。
8) 根据逻辑图与物理连接图(即根据物理区域邻接关系所确定的以各子区域为节点、子区域邻接关系为边的连通图)的映射关系,选择对于标记位置点具有最高平均定位精度的信号逻辑图为最优信号逻辑图。对于一个给定的标记位置点,其所对应的定位精度定义为:在该标记位置点上采集的能够正确定位到其所对应子区域的信号强度矢量个数与采集的信号强度矢量总数的比值,即:
| ${\rm{pro}}_{nc}^x = \frac{{nu_{co}^{nc}}}{{NR}}$ | (5) |
式中,proncx表示第x个待筛选信号逻辑图关于第nc个标记位置点的定位精度,nuconc为第nc个标记位置点上采集的能够正确定位到其所对应子区域的信号强度矢量个数;NR为第nc个标记位置点上采集的信号强度矢量总数。于是,对于所有标记位置点的平均定位精度为:
| ${\rm{pro}}_{{\rm{mean}}}^x = \frac{1}{{NC}}\sum\nolimits_{nc = 1}^{NC} {{\rm{pro}}_{nc}^x} $ | (6) |
在上节讨论的逻辑图构建步骤8)中,最优信号逻辑图的选择需要利用待筛选逻辑图与物理连接图的映射关系。该映射关系的构建过程如下:
1) 计算物理连接图中各子区域的邻接度(adjacent degree,AD)。对于一个给定的子区域,其邻接度定义为:该子区域与其邻接子区域在物理连接图中所对应的度数总和。定义子区域的最大和最小邻接度为Amag和Amig。
2) 对于第x(x=1,2,…,y)个待筛选逻辑图Grx,其中,y为待筛选逻辑图个数。同样,计算Grx中各逻辑节点的邻接度。对于一个给定的逻辑节点,其邻接度定义为:该逻辑节点与其邻接逻辑节点的度数总和。
3) 令Grx中逻辑节点的最大和最小邻接度为Amal和Amil,且将每个逻辑节点的邻接度VADl修正为VADg,即:
| ${V_{{\rm{ADg}}}} = {A_{{\rm{mig}}}} + \frac{{{A_{{\rm{mag}}}} - {A_{{\rm{mig}}}}}}{{{A_{{\rm{mal}}}} - {A_{{\rm{mil}}}}}}({V_{{\rm{ADl}}}} - {A_{{\rm{mil}}}})$ | (7) |
4) 对于一个给定的逻辑节点,选择物理连接图中与其具有最小邻接度距离的子区域,作为该逻辑节点的映射子区域,即该逻辑节点与此子区域具有映射关系。
5) 在物理连接图中,构建每个子区域与其余子区域的Floyd最短路径[7],并进而得到每个子区域所对应的中心区域节点,最后将得到的所有中心区域节点的并集,作为物理连接图所对应的中心区域节点。对于一个给定的子区域,其所对应的中心区域节点定义为:该子区域与其余子区域的Floyd最短路径的公共节点。
6) 在每个待筛选逻辑图中,构建每个逻辑节点与其余逻辑节点的Floyd最短路径,并进而得到每个逻辑节点所对应的中心逻辑节点,最后将得到的所有中心逻辑节点的并集作为该待筛选逻辑图所对应的中心逻辑节点。对于一个给定的逻辑节点,其所对应的中心逻辑节点定义为:该逻辑节点与其余逻辑节点的Floyd最短路径的公共节点。
7) 对于待筛选逻辑图中映射到非中心区域节点的中心逻辑节点,将其所映射的子区域修正为与其具有最小邻接度距离的中心区域节点。
在完成最优信号逻辑图与物理连接图的映射后,对于用户实时采集的信号强度矢量,首先计算其与不同逻辑节点类心的欧式距离,确定最小类心欧式距离所对应的逻辑节点,然后利用逻辑节点与子区域的映射关系,估计用户位置所属子区域。
1.4 基于Graph Drawing正交算法的图形绘制为了提高最优逻辑图与物理连接图结构的可读性和可靠性,本文采用graph drawing正交算法[7]对逻辑图和物理连接图进行绘制,具体步骤如下:
1) 对于初始图(即最优信号逻辑图或物理连接图)G=(V,E),随机选择两个节点s和t,其中,V={vei}(i=1,2,…,nve)和E={edj}(j=1,2,…,ned)分别为G中的点集和边集,vei表示G中第i个节点,edj表示G中第j条边,nve和ned分别表示G中节点及边的数目。
2) 在G中搜索得到包含s的边及这些边包含的节点,以s为源点且以这些边包含的节点为终点作有向边,然后,在所有终点中选择不为t的终点作为新的起点。
3) 对于每一个新的起点,搜索得到包含该起点的边及这些边包含的节点,以该起点为源点且以这些边包含的节点为终点作有向边,当某条有向边的两个端点均为新的起点时,规定从左往右或从上往下绘制该有向边,然后,在所有终点中选择不为t的终点作为新的起点。
4) 重复步骤3),得到最终有向图G'。
5) 对图G'中每条有向边的两个端点赋值,且要求:① 每条有向边的终点赋值大于起点赋值;② s的值为0;③ 终点赋值的最大值与起点赋值的最小值的差值达到最小[7]。
6) 构造另一无向图${D_\prod }$。过程如下:
图${D_\prod }$的三部分点集为:① 图G'中边所构成的所有最小区域,其中最小区域定义为:不存在其余边对该区域进行分割的封闭区域;② 图G'外部空间所形成的两个邻近区域,且满足:两个邻近区域的并集为图G'外部空间、s和t在两个邻近区域的边界上。不妨令两个邻近区域中的左边区域(或上边区域)为s*,右边区域(或下边区域)为t*,有s*$ \cup $t*=图G'外部空间。s*的边界包含3段:第1段为连接s与t的最左边(或最上边)的无向路径$\prod '$;第2段为连接s与s'的任意一条无向边路径$\prod ''$,其中s'为图G'外部空间的任意一点、$\prod ''$包含于图G'外部空间、s'与s的路径长度趋于无穷大;第3段为连接t与t'的任意一条无向边路径$\prod '''$,其中,t'为图G'外部空间的任意一点、$\prod '''$包含于图G'外部空间、t'与t的路径长度趋于无穷大、t'与t的路径和s'与s的路径不相交;③ 图G'中的路径[8] 。
图${D_\prod }$的两部分边集为:① 遍历图${D_\prod }$中第3部分点集(即图G'中tnu条路径),若第tnu1(tnu1=1,2,…,tnu)条路径${\prod _{{\rm{tnu1}}}}$中的某一条边包含于图${D_\prod }$中某第1或第2部分点所对应区域的边界,则在${D_\prod }$中以该第1或第2部分点为一点、${\prod _{{\rm{tnu1}}}}$所对应的第3部分点为另一点作无向边;② 遍历图${D_\prod }$中第1和第2部分点集(即图G'中anu个区域),若第an1(an1=1,2,…,anu)个区域Aan1边界中的某一条边包含于图${D_\prod }$中某第3部分点所对应的路径,则在${D_\prod }$中以该第3部分点为一点、Aan1所对应的第1或第2部分点为另一点作有向边;最后令s= s*、t= t*且G=${D_\prod }$,重复第2)步至第4)步得到关于图${D_\prod }$的有向图${D_{\prod '}}$。
7) 对图${D_{\prod '}}$中每条有向边的两个端点赋值,且要求:① 每条有向边的终点赋值大于起点赋值;② s*的赋值为-0.5;③ 终点赋值最大值与起点赋值最小值之差达到最小。
8) 遍历图G'中所有节点,对每一个节点其纵坐标为该点在G'中的赋值,横坐标有两个,分别为包含该点的路径在${D_{\prod '}}$中赋值的最大值和最小值,连接该最大值和最小值所分别对应的两个坐标位置,即得关于该节点的坐标表示线。同样,遍历图G'中所有边,对于每一条边,其横坐标为该边在${D_{\prod '}}$中的赋值,纵坐标有两个,分别为该边在G'中起点和终点赋值,连接该起点和终点赋值所分别对应的两个坐标位置,即得关于该边的坐标表示线。
9) 根据G'中所有节点和边的坐标表示线,标记新的节点,且连接不同新的节点的坐标表示线即为新的边。新的节点位置的选取规则为:对于每一条点的坐标表示线,新节点位置为与该点的坐标表示线相交的边的坐标表示线的交点上。
2 实验结果及分析利用在某一WLAN室内环境下随机采集的21条接收信号强度序列进行实验,选择的标记位置点个数为2(小于子区域个数7),分别位于子区域1和5,如图 5所示。实验中将定位目标区域划分为7个子区域,分别标记为1,2,…,7。
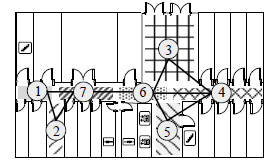 |
| 图5 定位目标区域划分 |
图 6为利用graph drawing正交算法得到的定位目标区域所对应的物理连接图。图 7为基于graph drawing正交算法的最优信号逻辑图的绘制结果。此外,为了说明graph drawing正交算法的有效性,图 8为某一结构较复杂的待筛选信号逻辑图在经graph drawing正交算法绘制前和绘制后的图形结构。可见,graph drawing正交算法能够更好的呈现节点间的几何依赖关系,尤其是对于节点数较多且节点连接关系较复杂的图形结构,使得其具有更好的可读性。
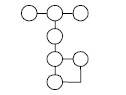 |
| 图6 基于graph drawing绘制的物理连接图 |
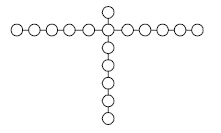 |
| 图7 基于graph drawing绘制的最优信号逻辑 |
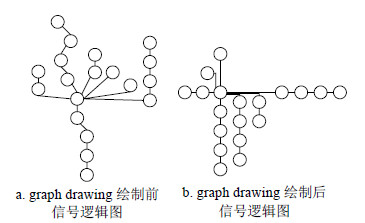 |
| 图8 基于Graph Drawing绘制前及之后的某一待筛选信号逻辑图 |
为了验证本文映射准则的可靠性,图 9给出了物理子区域3中所采集的来自5个不同AP(AP位置如图 8所示)的信号强度值的概率分布,图 10给出了子区域3所对应逻辑节点所包含的来自5个不同AP的信号强度值的概率分布。可看出,物理子区域3中所采集的信号强度分布与其对应逻辑节点所包含的信号强度分布具有较好的相似特性,例如,关于AP4的信号强度值均主要集中在-70dBm~-60dBm的区间段内,且具有相似的概率分布特性。充分说明了本文所建立的信号逻辑图与物理连接图映射关系的合理性,此外,利用该映射关系,还可实现对用户所属区域的定位。
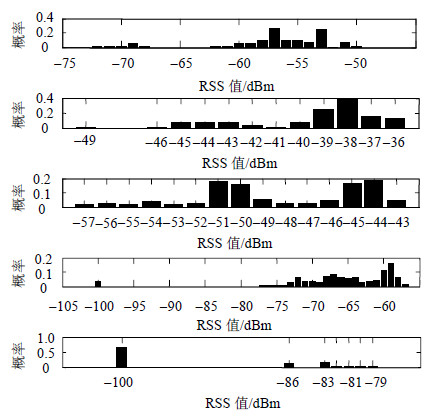 |
| 图9 物理子区域3中所采集的信号强度分布 |
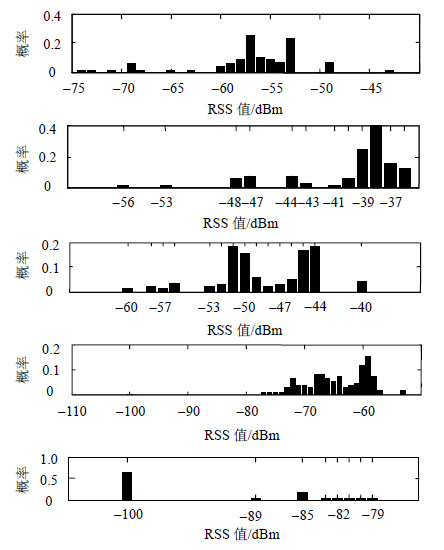 |
| 图10 物理子区域3所对应逻辑节点所包含的信号强度分布 |
图 11给出了在传统层次聚类映射[9]、K均值聚类映射[10]以及本文提出的时间戳标记的谱聚类映射条件下的子区域平均正确定位概率。时间戳信息的引入,一定程度上能够改善聚类效果,进而提高系统的定位性能。可看出当时间戳信息的权重设为0.9时,基于谱聚类映射的子区域平均正确定位概率约为73.08%,显著优于基于层次聚类映射和K均值聚类映射的定位结果,精度提高近25%。
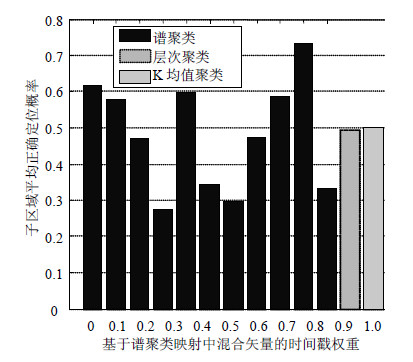 |
| 图11 不同聚类映射条件下的子区域平均正确定位概率 |
由于传统位置指纹数据库构建的耗时性和人力开销限制了在WLAN室内环境中基于信号强度定位算法的扩展及应用,而基于即时定位与地图构建的定位系统存在对用户终端设备要求较高等问题。针对上述问题,本文提出了一种基于图像边缘检测的WLAN室内用户运动地图构建及映射方法。通过算法分析及实验结果,可得本文方法无需位置指纹和运动传感器辅助,且在选择合理时间戳权重的条件下,其定位精度优于基于传统层次聚类映射和K均值聚类映射的定位方法,即本文方法能够较好地实现对WLAN室内用户位置的有效估计,同时本文采用graph drawing正交算法增强了用户运动地图的可读性和可靠性。此外,利用半监督学习方法对信号逻辑图与物理连接图映射关系的自适应更新,以及利用绘图技术对用户运动行为进行分析是下一步工作内容。
| [1] | FELIX D, MCGUIRE M. Received signal strength calibrat-ion for handset localization in WLAN[C]//The 47th IEEE International Conference on Communication. Ottawa, Canada: Institute of Electrical and Electronics Engineers Incorporated, 2012: 3664-3669. |
| [2] | FANG S, LIN T. Principal component localization in indoor WLAN environments[J]. IEEE Transactions on Mobile Computing, 2012, 11(1): 100-110. |
| [3] | CHEN Q, HUANG G, SONG S. WLAN user location estim-ation based on receiving signal strength indicator[C]//The 5th International Conference on Wireless Communications, Networking and Mobile Computing. Beijing: IEEE, 2009: 1-4. |
| [4] | WU C, YANG Z, LIU Y, et al. WILL: Wireless indoor localization without site survey[J]. IEEE Transactions on Parallel and Distribution System, 2013, 24(4): 839-848. |
| [5] | BRUNO L, ROBERTSON P. Observability of path loss parameters in WLAN-based simultaneous localization and mapping[C]//International Conference on Indoor Positioning and Indoor Navigation. Montbeliard-Belfort, France: IEEE, 2013: 1-10. |
| [6] | LUXBURG U V. A tutorial on spectral clustering[J]. Statistics and Computing, 2007, 17: 395-416. |
| [7] | WANG J, SUN Y, LIU Z, et al. Route planning based on Floyd algorithm for intelligence transportation system[C]//IEEE International Conference on Integration Technology. Shenzhen: Institute of Electrical and Electronics Engineering Computer Society, 2007: 544-546. |
| [8] | HERMAN I, MELANCON G, MARSHALL M S. Graph visualization and navigation in information visualization: a survey[J]. IEEE Transactions on Visualization and Computer Graphics, 2000, 6(1): 24-43. |
| [9] | LAZAREVIC A, KANAPADY R, KAMATH C, et al. Localized prediction of continuous target variables using hierarchical clustering[C]//The 3rd IEEE International Conference on Data Mining. Melbourne, United States: Institute of Electrical and Electronics Engineers Incorporated, 2003: 139-146. |
| [10] | MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]//The 5th Berkeley Symposium on Mathematical Statistics and Probability. California, USA: University of California Press, 1967: 281-297. |
 2016, Vol. 45
2016, Vol. 45
